华为OD机试真题(C卷,100分)- 生成哈夫曼树（Java & JS & Python & C）_华为od机试 python 给定长度为 n 的无序的数字数组,每个数字代表二叉树的叶子节点

华为OD机试真题(C卷,100分)- 生成哈夫曼树（Java & JS & Python & C）

题目描述

给定长度为 n 的无序的数字数组，每个数字代表二叉树的叶子节点的权值，数字数组的值均大于等于1。

请完成一个函数，根据输入的数字数组，生成哈夫曼树，并将哈夫曼树按照中序遍历输出。

为了保证输出的二叉树中序遍历结果统一，增加以下限制：

二叉树节点中，左节点权值小于右节点权值，根节点权值为左右节点权值之和。当左右节点权值相同时，左子树高度小于等于右子树高度。

注意：

所有用例保证有效，并能生成哈夫曼树。

提醒：

哈夫曼树又称为最优二叉树，是一种带权路径长度最短的二叉树。

所谓树的带权路径长度，就是树中所有的叶节点的权值乘上其到根节点的路径长度（若根节点为 0 层，叶节点到根节点的路径长度为叶节点的层数）

输入描述

例如：由叶子节点：5 15 40 30 10，生成的最优二叉树如下图所示，该树的最短带权路径长度为：40 * 1 + 30 * 2 + 5 * 4 + 10 * 4 = 205。

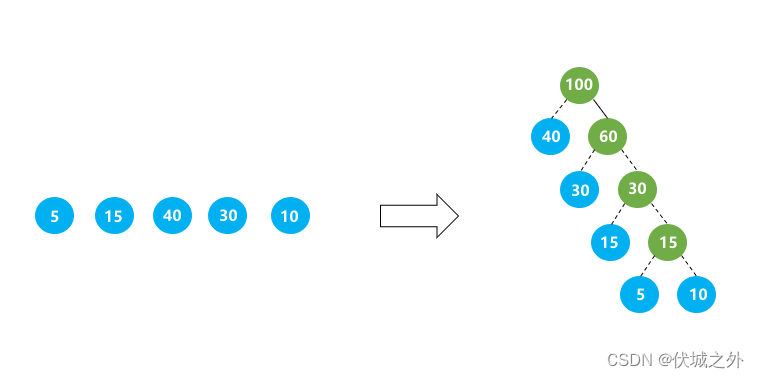
输出描述

输出一个哈夫曼树的中序遍历数组，数值间以空格分隔

用例

5 15 40 30 10
|
|
输出
|
40 100 30 60 15 30 5 15 10
|
|
说明
|
根据输入，生成哈夫曼树，按照中序遍历返回。所有节点中，左节点权值小于等于右节点权值之和。当左右节点权值相同时，左子树高度小于右子树。结果如上图所示。
|

题目解析

本题主要是考察哈夫曼树的构建。

哈夫曼树定义：

给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。

比如题目用例给出的N个叶子节点的权值分别为：5 15 40 30 10

那么我们可以根据这些叶子节点任意构造一个二叉树，比如下图所示

那么这颗二叉树的各个叶子节点的带权路径长度如下：

5*3 + 15*3 + 40*3 + 30*3 + 10*1 = 280

因此这颗二叉树的带权路径长度 = 280 要比题目描述中构造的最优二叉树的205大。因此这种二叉树就不是哈夫曼树。

---

哈夫曼树是根据给定的n个叶子节点构造出的带权路径长度最短的二叉树。

而哈夫曼的构建是有固定思路：

首先，我们从给定的n个叶子节点的权值序列中取出最小的两个，

比如 [5, 15, 40, 30, 10] 中最小的两个是5、10，取出进行合并，则可得如下新节点15（绿色），

然后将新节点重新加入到权值序列中，得到红框中新序列 [15, 15, 40, 30]

然后再从新序列 [15, 15, 40, 30]中取出最小的两个，进行合并

---

然后再从新序列 [30, 40, 30]中取出最小的两个，进行合并

---

然后再从新序列 [60, 40]中取出最小的两个，进行合并

---

此时序列中只剩下一个节点，即可停止上面逻辑。

按照这种策略构造出来的二叉树的带权路径长度是最短的，即构建出来的是哈夫曼树。

另外，如果初始有N个叶子节点的话，那么构造出来的哈夫曼树的节点总数就有 2 * N - 1 个。

其实，我们通过上图就可以发现规律，蓝色节点是初始N个叶子节点，绿色节点是新建的，而绿色节点的个数 = N - 1。

了解了哈夫曼树的构造原理后，其实本题就很简单了，只需