- 1数据结构---双链表
- 2MySQL表的增删改查(初阶)
- 3SPI
- 4html实验:百度API定位+获取摄像头拍照_html获取摄像头并添加地理位置
- 5微信小程序授权登录获取用户的openid_小程序获取openid
- 6python小游戏开心消消乐制作9-连接路径和广度优先搜索_广度优先搜索 游戏
- 7idea Git is not installed_git is not installed unsupported format of git --v
- 8网络安全人士必知的35个安全框架及模型(建议收藏)_网络安全架构
- 9安装pyspark过程,超级easy_pyspark 安装
- 10【NLP】强推!大语言模型『百宝书』,一文缕清所有大模型!
2023-10-26-雷达检测-CFAR算法_caso cfar
赞
踩
Written by author:由于作者还是学生,研究的方向是毫米波雷达,因此作者希望通过每周写一篇博客的形式来记录并巩固自己每天所学习的知识,同时也锻炼自己的总结能力,故文中可能会出现一些理论上的错误或者引用错误,恳请读者指正!!
1、前言
上篇文章简单介绍了MUSIC算法的基础版本,本篇文章将会介绍雷达信号处理检测中的一个重要的算法-CFAR。恒虚警检测(Constant False Alarm Rate, CFAR)是一个比较经典的算法,作者会简单介绍一下CFAR的基本原理和一些相关的CFAR算法。由于代码网上已经有了很多,所以本文中的代码会引用其他大佬们的成果,会在文末对他们进行引用与致谢。
2、简介
在学习CFAR之前,我们需要了解一些基础知识。
2.1、目标检测的概念
雷达检测在雷达算法中有着举足轻重的地位,其可以被认为是雷达信号处理与数据处理的分水岭,其输入为信号处理的结果,输出为数据处理的输入。它的主要作用就是去除掉杂波的干扰。
目标检测的核心思想就是阈值法。如果雷达回波大于阈值,则显示为检测到目标,反之视为噪声。
2.2、基于固定门限的目标检测
基于固定门限的目标检测是经典的自动检测方法,该方法通过设置一个固定的功率阈值,将接收信号功率与该阈值进行比较,接收信号功率大于阈值则判别为雷达回波信号,反之视为噪声与杂波。
从另一个角度来说,该问题可以建模为一个二元假设问题。
设接收机输出信号(接收信号)由表示,
一般由背景噪声信号
与雷达回波信号
表示。
一般存在两种情况。
当只有噪声时:
当存在雷达回波信号时:
下面我们定义四个参数
:假设接收机无信号输入
:假设接收机有信号输入
:检测器做出无信号判决结果
:检测器做出有信号判决结果
当回波信号只有噪声的时候,门限判决把噪声分为两种情况
当回波信号只有信号的时候,门限判决把信号也分为两种情况
那么正常会出现四种情况
| 不报警 | 错警 | |
| 漏警 | 检测 |
1.为真,判为
,即接收机无信号输入,检测器判为无信号,称为正确不发现;
2.为真,判为
,即接收机无信号输入,检测器判为有信号,称为虚警;
3.为真,判为
,即接收机有信号输入,检测器判为无信号,称为漏警;
4.为真,判为
,即接收机有信号输入,检测器判为有信号,称为正确检测;
其中1和4是正确的情况,其他两种情况属于错误的判决。
存在回波信号的时候接收信号
的概率密度函数为
。
不存在回波信号的时候接收信号
的概率密度函数为
。
下图为两个概率密度的几何关系图:

可以看出虚警率和检测率
可以表示为:
其中,T为检测门限,由极小化平均损失产生的贝叶斯判决准则获得的似然比为:
门限判决条件可以被表示为:
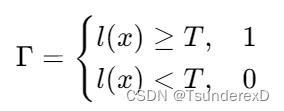
其中,表示为存在目标,
表示为不存在目标。
雷达回波总是含有噪声,噪声会引起错警和漏检,但同时降低虚警概率与提高检测概率之间存在矛盾,因此需要精心设计阈值
对于单个数据样本的最简单情况,虚警高氯为,其中T是检测阈值,因此,固定虚警率阈值为:
对于未标准化的数据样本和绝对率检测器,阈值是
其中, 是干扰的总噪声功率。虚警概率为
,检测过程如下图所示。

可以看出,阈值T与噪声功率成正比。当雷达接收机输出的干扰发生变化时,实际会发生很大幅度的变化,对于雷达系统来说,当
干扰增加时,假警报的数量也会增加,因此,应该调整固定阈值来保持所需要的
,也就是虚警率。
然而,实际过程中的雷达信号往往是不知道其概率密度函数的,大多数回波信号都是噪声,我们并不能像上面那样确定一个合适的判决门限,因此我们可以换个角度,从噪声的角度来下手这个问题。我们可以计算回波信号的统计特性,从高斯分布与标准差的关系来入手。
一个高斯分布的标准差,其标准差始终和概率密度函数相互联系起来,也就是说,随着噪声的统计特性起伏变化,标准差也在起伏变化,如果我们把门限定为就可以确定一个恒定的虚警概率,这就是CFAR的核心思路。保证虚警率一致,并且随着外部环境噪声自适应的起伏(标准差本身就是随着环境自适应起伏)。
在实际工程中,将信号与阈值相比较是比较快的一种方法,阈值的计算过程中已经包含了虚警率和检测概率。对雷达系统来说,阈值的选择目的在于保证最大的检测概率和尽可能小的合适的虚警率,之前的讨论都是基于理想状态下,已经方差已知的高斯白噪声。实际的过程中与理论有很大差距,功率都是未知的,因此提出CFAR来解决这个问题。
2.3、CFAR检测
目前比较常见的CFAR检测算法分为两类:
一类是均值类型的CFAR算法,该类算法应用的前提是假设背景杂波是均匀分布的。
另一类是有序统计类CFAR(OS-CFAR)算法,这类算法主要是为了计算多目标。
本文会介绍基本的均值CFAR算法和OS-CFAR算法。
CFAR算法的基本思想是:对每个雷达测量的数据点,以该点为中心,建立一个检测窗口,在该窗口内计算信号的平均值与方差。并将该窗口分为若干个子窗口。然后,根据期望的虚警率和背景噪声的统计特性,计算每个子窗口的阈值,进行判断每个子窗口内是否存在目标信号。
2.3.1 CA-CFAR
下图是均值CFAR检测器的方框图。其中一些定义需要大家知道。
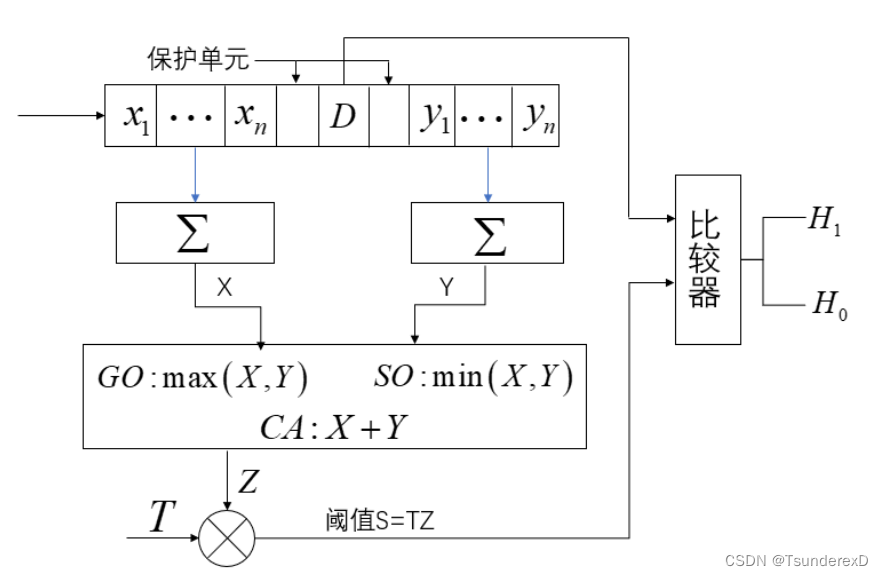
如图,输入信号被送到一个延迟线中,延迟线由(2n+1)个延迟单元构成,其中中间的D为被检单元,检测单元旁边的两个单元称为保护单元(防止目标能量泄露影响参考单元效果), 在旁边的2n个单元称为参考单元(其中左侧n个单元也叫做前沿参考窗,同理右侧n个单元叫做后沿参考窗)用R表示参考单元的长度,R=2n。前沿和后沿参考单元 对杂波强度的局部估计分别用X和Y表示,检测门限 S=TZ,要改变检测门限的大小可以通过调整门限因子T的大小。
CA-CFAR是将参考床内所有参考单元的采样值取平均作为背景的功率水平估计Z,即:
则待检测单元的检测门限为:
为计算方便对其进行变换,定义,则有
,在
无目标假设下,根据概率论相关知识可以得到
PDF为:
由独立同分布的随机变量联合概率密度函数,结合概率论相关知识可得T的PDF服从厄兰密度函数,即:
在估计的门限下所对应的虚警概率也是一个随机变量,其数学期望为:
解这个标准积累式并作代数运算可得最终结果为:
对于给定的预期虚警概率和参考单元数N,可得对应的门限乘积因子
:
从倒数第二个式子可以看出,虚警概率的期望并不依赖于实际干扰的功率,仅与参与单元平均参考单元数N以及门限乘积因子 有关,这说明单元平均恒虚警处理技术体现了CFAR的特点,利用
可以得到待检测单元的检测门限。
CA-CFAR容易受到杂波边缘的影响而增加虚警,还会因为CA窗中存在目标或脉冲干扰而失去灵敏性。只有杂波在空间上均匀或其变化比单元窗的长度要慢时,该结构才能正常工作。同时由于检测到杂波临界时,CA-CFAR会造成虚警率的大幅上升的结果,并且在目标数目较多的检测背景中使用单元平均恒虚警处理 器会使目标检测概率大大下降.
2.3.2 GO-CFAR
最大选择GO(Greatest Of)-CFAR是选取前面n个参考单元之和与后面n个参考单元之和中的较大者作为背景杂波功率水平Z
最小选择SO(Smallest Of)-CFAR是选取前面n个参考单元之和与后面n个参考单元之和中的小者作为背景杂波功率水平Z。
对GO-CFAR算法,在均匀环境假设下,由于Xi独立同分布,所以X和Y同样也是独立分布的,根据概率论公式有
可以求得Z的矩母函数,进而可以求得GO-CFAR在均匀环境中的虚警概率为:
根据上式给定预期虚警概率就可以求解门限乘积因子进而计算检测门限。
该检测器的优点在于能广泛应用于在杂波转换期间(也就是杂波边缘)限制虚警, 然而也同样存在缺点。即容易受到 CFAR 窗内干扰目标的影响,因此 GO-CFAR 检测 器对于两个相邻目标会很难进行分辨。
2.3.3 SO-CFAR
同理,可以求得SO-CFAR算法
SO-CFAR 检测器选择被测单元两边估计出的平均值中的最小值生成门限。该检测器虽然能够分辨紧靠在一起的目标,但在杂波边缘时,虚警率会很高。
2.3.4 OS-CFAR
OS-CFAR算法如下图:
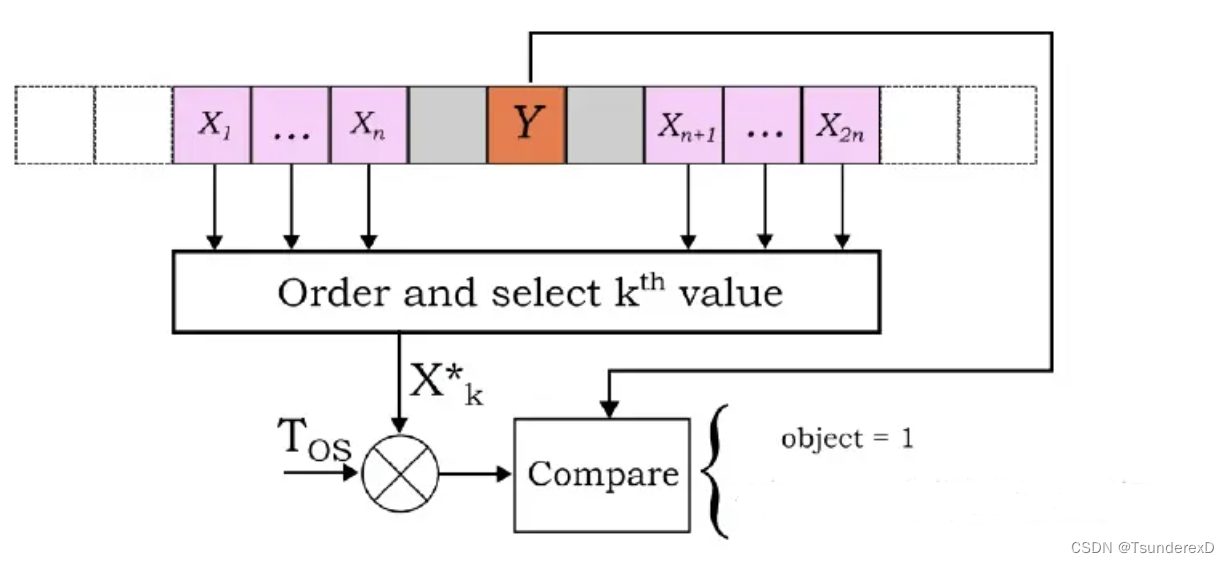
该算法将所有参考单元的所有幅度按照升序排列,然后选择第K个值,如下:
其中K按照下述公式来计算,可以保证最小虚警率:
门限因子可以通过递归数值求解下式得到:
OS-CFAR 算法在非均匀情况下有更好的性能,即当存在存在多个目标。 缺点是它的计算时间较长,因为它有更多要做的计算。 因此,它可能不太适合实时应用程序,具体取决于所需的速度。且其杂波边缘区域虚警概率也会较高。
2.3.4 杂波图CFAR
经典的空域杂波图CFAR算法,假设每个距离元和方位角上的平方率值遵从独立同分布,通过对时间维上的数据进行遗忘迭代来拟合杂波背景噪声。
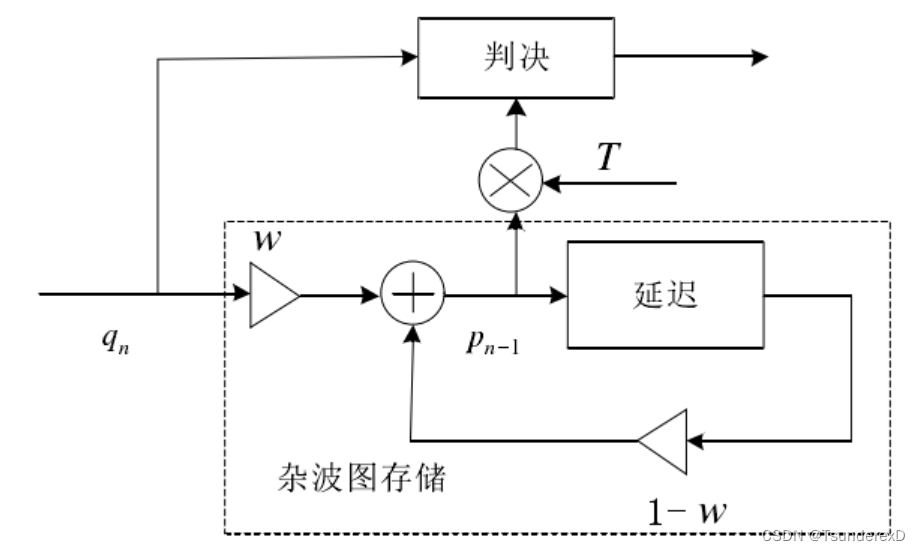
优点:通过提高累积帧数,杂波背景噪声功率趋近于理论值
缺点:对于慢移动目标有自遮掩效果
具体推导请读者自己去参阅相关参考文献,这里不再详解。
3、总结
理想情况下的CFAR算法:
①多目标检测性能很好,几乎互不影响;
②杂波边缘区域,突变很快,虚警率稳定;
③慢移动目标自遮掩改善;
④算法实用,复杂度适中,理论可实现
实际的CFAR算法

实际中,根据多方面考量,用的最多的还是CA-CFAR算法。
本文主要CFAR的一些简单的原理,具体的matlab代码请自行去搜索。
本文主要是作者自己的一些知识点的积累,具体详细的推导过程请移步:
《雷达信号处理基础》 邢孟道,王彤,李真芳
《雷达信号处理和数据处理技术》 吴顺君
4、参考文献
1.【精选】【目标检测】雷达目标CFAR检测算法-CSDN博客
2.雷达无线电系列(二)经典CFAR算法图文解析与实现(matlab) - 万雨 - 博客园
3.王蓓. 基于杂波图的恒虚警处理技术研究[D]. 西安电子科技大学, 2018.
4.雷达信号处理之恒虚警(CFAR)检测基础知识总结 - 知乎 (zhihu.com)
5.【雷达目标检测】恒定阈值法和恒虚警(CFAR)法及代码实现
6.【精选】恒虚警检测(Constant False Alarm Rate, CFAR)-CSDN博客
在此感谢各位大佬分享的文章。


