损失次数模型-二项分布_损失次数分布的理论次数怎么算

损失次数模型-二项分布

——非寿险精算的基本理论

1、定义

在$n$次独立重复的伯努利试验中，设每次试验中事件A发生的概率为$p$。用$X$表示$n$重伯努利试验中事件A发生的次数，随机变量$X$的离散概率分布即为二项分布。

• 上述定义提到了伯努利试验，伯努利试验的特点是：

（1）每次试验中事件只有两种结果；

（2）每次试验中事件发生的概率是相同的；

（3）$n$次试验的事件相互之间独立。

2、概率密度函数

$P(X=k)=C_n^k{p}^k(1-p{)}^{n-k}$

• 公式释义：

$n$：一组实验中，实验次数为$n$；

$k$：$n$次实验中，成功的次数为$k$；

$p$：一次伯努利实验中，成功的概率；

$1-p$：一次伯努利实验中，失败的概率；

一次伯努利试验只有两个结果，成功或失败。成功的概率为$p$，则失败的概率就是$1-p$

$P(X=k)$：一组n次伯努利实验中，成功次数为$k$的概率；

• 例子

我们现在做一组5次抛硬币实验，每次实验中正面向上的概率为0.5，则5次实验中，4次正面向上的概率是多少？

1）首先判断是不是伯努利实验

<结合伯努利实验的性质一一对照看一下>

• 每次试验中事件只有两种结果；是的，要么正面向上，要么反面向上

• 每次试验中事件发生的概率是相同的；是的，每次正面向上的概率都是0.5

• $n$次试验的事件相互之间独立。是相互独立的，第一次实验的结果不会影响到第二次抛硬币实验的结果

2）带入公式求解

$P(X=4)=C_5^{4}0.5^4(1-0.5{)}^1=0.15625$

补充一个公式：$C_n^m=\frac{n!}{m!(n-m)!}$

<公式理解>

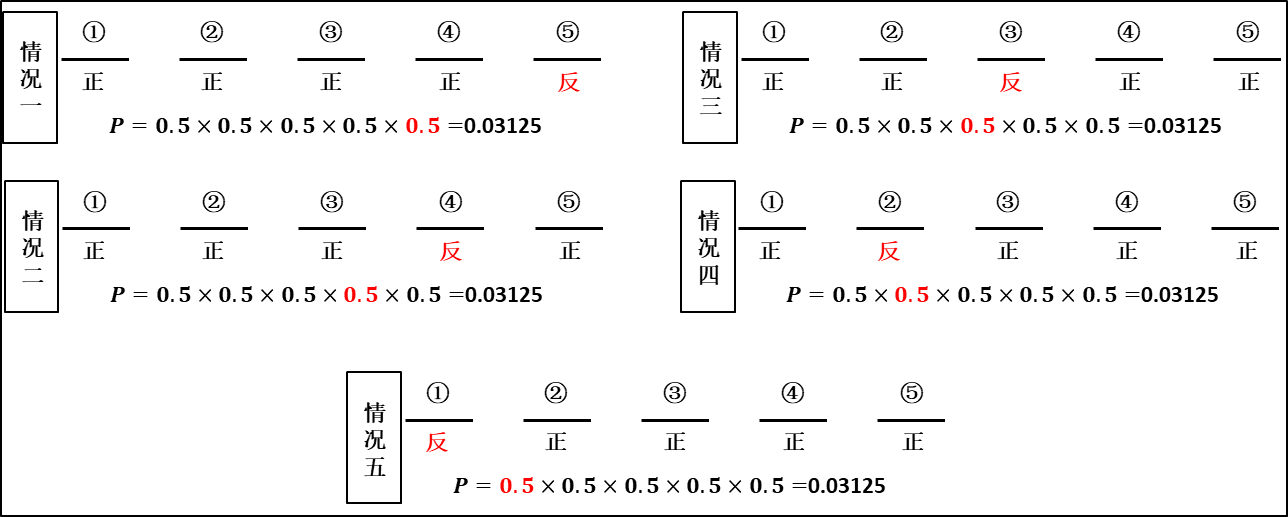
5次抛硬币实验中，4次正面向上的事件，一共有5种可能情况，每种情况可参考下图。每种情况发生的概率都为0.03125，五种情况加在一起就是0.03125*5=0.15625。五种情况对应的公式就是$C_5^4=5$，然后乘以每次实验的概率，就是5次抛硬币实验中，有4次正面向上的概率。

3、均值和方差

$$E(X)=np$$

$$D(X)=np(1-p)$$

3.1、均值$E(X)$的推导

$E(X)=\sum xp(x)$

这个公式在前面介绍泊松分布的时候提及了一下，但并没有展开说明，有兴趣的可以再去回顾一下概率论知识。

把$P(X)=C_n^x{p}^x(1-p{)}^{n-x}$带入上式，可得

$=\sum x{C}_n^x{p}^x(1-p{)}^{n-x}$

因为$C_n^m=\frac{n!}{m!(n-m)!}$，所以$C_n^x=\frac{n!}{x!(n-x)!}$，则

$=\sum x\frac{n!}{x!(n-x)!}{p}^x(1-p{)}^{n-x}$

然后，$n!=n(n-1)!$，$p^x=p{p}^{x-1}$，带入上式

$=\sum x\frac{n(n-1)!}{x!(n-x)!}p{p}^{x-1}(1-p{)}^{n-x}$

将$np$移到$\sum$前面，得到

$=np\sum x\frac{(n-1)!}{x!(n-x)!}{p}^{x-1}(1-p{)}^{n-x}$

因$x\frac{(n-1)!}{x!(n-x)!}=x\frac{(n-1)!}{x(x-1)!(n-x)!}=\frac{(n-1)!}{(x-1)!(n-x)!}=C_{n-1}^{x-1}$，得到

$=np\sum C_{n-1}^{x-1}{p}^{x-1}(1-p{)}^{n-x}$

令$n-1=m，x-1=k$，得

$=np\sum C_m^k{p}^k(1-p{)}^{n-1-(x-1)}$

$=np\sum C_m^k{p}^k(1-p{)}^{m-k}$

$C_m^k{p}^k(1-p{)}^{m-k}$，是不是和$P(X=k)=C_n^k{p}^k(1-p{)}^{n-k}$形式一模一样，所以$C_m^k{p}^k(1-p{)}^{m-k}=P(X=k)$，则

$=np\sum P(X=k)$

$\sum P(X=k)$是二项分布所有情况下得概率和，因此其值为1，即$\sum P(X=k)=1$，所以

$=np\sum P(X=k)=np$

3.2、方差$D(X)$的推导

根据之前泊松分布里面的文章，我们知道$D(X)=E(X^2)-(E(X){)}^2$，现在$E(X)$已经求出，因此只需推导$E(X^2)$即可。

$E(X^2)=\sum x^{2}p(x)$

这个公式我也曾在泊松分布这篇文章里面提到过，有兴趣的可以去查看。

把$P(X)=C_n^x{p}^x(1-p{)}^{n-x}=\frac{n!}{x!(n-x)!}{p}^x(1-p{)}^{n-x}$带入上式

$=\sum x^2\frac{n!}{x!(n-x)!}{p}^x(1-p{)}^{n-x}$

把$p^x=p{p}^{x-1},n!=n(n-1)!$带入上式

$=\sum x^2\frac{n(n-1)!}{x!(n-x)!}p{p}^{x-1}(1-p{)}^{n-x}$

将$np$移到$\sum$前面，得到

$=np\sum x^2\frac{(n-1)!}{x!(n-x)!}{p}^{x-1}(1-p{)}^{n-x}$

因$x^2=xx,x!=x(x-1)!$所以

$=np\sum xx\frac{(n-1)!}{x(x-1)!(n-x)!}{p}^{x-1}(1-p{)}^{n-x}$

因$x$分子和分母可以约掉，所以

$=np\sum x\frac{(n-1)!}{(x-1)!(n-x)!}{p}^{x-1}(1-p{)}^{n-x}$

因$x=x-1+1$，所以

$=np\sum (x-1+1)\frac{(n-1)!}{(x-1)!(n-x)!}{p}^{x-1}(1-p{)}^{n-x}$

$=np\sum (x-1)\frac{(n-1)!}{(x-1)!(n-x)!}{p}^{x-1}(1-p{)}^{n-x}+np\sum \frac{(n-1)!}{(x-1)!(n-x)!}{p}^{x-1}(1-p{)}^{n-x}$

这一部分$\sum \frac{(n-1)!}{(x-1)!(n-x)!}{p}^{x-1}(1-p{)}^{n-x}$在求解$EX$时，已经推导，其值为1，所以

$=np\sum (x-1)\frac{(n-1)!}{(x-1)!(n-x)!}{p}^{x-1}(1-p{)}^{n-x}+np$

因$(n-1)!=(n-1)(n-2)!,(x-1)!=(x-1)(x-2)!,p^{x-1}=p{p}^{x-2}$，所以

$=np\sum (x-1)\frac{(n-1)(n-2)!}{(x-1)(x-2)!(n-x)!}p{p}^{x-2}(1-p{)}^{n-x}+np$

$(x-1)$分子分母消掉，$(n-1)p$提到$\sum$前面，得

$=np(n-1)p\sum \frac{(n-2)!}{(x-2)!(n-x)!}{p}^{x-2}(1-p{)}^{n-x}+np$

令$n-2=m，x-2=k$，得

$=np(n-1)p\sum \frac{m!}{k!(m-k)!}{p}^k(1-p{)}^{m-k}+np$

这一部分$\sum \frac{m!}{k!(m-k)!}{p}^k(1-p{)}^{m-k}$，在求解$EX$时，已经知道其值为1，所以

$=np(n-1)p+np=n^2{p}^2-n{p}^2+np$

因此：

$D(X)=E(X^2)-(E(X){)}^2$

$=n^2{p}^2-n{p}^2+np-n^2{p}^2$

$=np(1-p)$

4、二项分布在精算中的应用

4.1、定义

假设损失次数$N$服从参数为$n和p$的二项分布，则发生$k$次损失的概率为:
$$P(N=k)=C_n^k{p}^k(1-p{)}^{n-k}$$

二项分布的均值和方差为：

$E(N)=np$

$D(N)=np(1-p)$

4.2、性质

（1）方差小于均值。这是他与泊松分布和负二项分布在实际运用中的主要区别。泊松分布的方差等于均值，负二项分布的方差大于均值。

（2）假设每个风险发生损失的概率均为$p$，则二项分布可以描述$n$个独立同分布的风险所组成的风险集合的损失次数。这句话其实我没有理解通透。

（3）如果用二项分布描述损失次数，则意味着损失次数存在一个最大值，这就是二项分布的参数$n$。

5、软件实操

5.1、相同的$n$，不同的$p$

画图代码

import numpy as np
import math
import matplotlib.pyplot as plt

def bpmf(max_k,n,p):
    '''
    Parameters
    ----------
    max_k : int
        二项分布中，实验成功的最大次数.
    n : int
        二项分布的实验次数.
    p : float
        二项分布中，每次实验的成功的概率.

    Returns
    -------
    k: list
        二项分布中，成功次数.
    probability : lsit
        二项分布中，对应成功次数的概率.
    '''
    
    sample=max_k
    n=n
    p=p
    k_sample=np.arange(sample+1)#会返回一个0至sample的连续整数列表
    probability=[]
    for k in k_sample:
        temp = (math.factorial(n)/(math.factorial(k)*math.factorial(n-k)))*p**k*(1-p)**(n-k)#计算二项分布的概率
        #math.factorial()是阶乘函数
        probability.append(temp)
    return k_sample,probability
  
n=30
max_k=n
plt.subplot(1,1,1)#定义图片的布局，针对一张图片来说可以省略该代码
p=0.3
k,probability=bpmf(max_k,n,p)#调用自定义的二项分布函数
plt.plot(k,probability,"r",label="p="+str(p))#画曲线图，并定义曲线为红色"r"，并显示图例label（后面是图例名称）
plt.plot(k,probability,"ro")#画散点图，并定义散点为红色
plt.title("Binomial distribution(n="+str(n)+")")#设置图片标题
plt.xlabel("Number of successes (k)")#设置图片x轴说明
plt.ylabel("probability")#设置图片y轴说明
plt.legend(loc=0)#将图例放在合适的位置，让系统自动查找
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

输出结果

从图片可以看出，当实验次数$n$一定时，随着成功的概率$p$的变大，函数图像逐渐向右移动（均值变大）。

5.2、相同的$p$，不同的$n$

代码与上面相同，只是保持$p$不变，而修改了$n$值和图像表头

输出结果

从图片可以看出，当$p$保持不变时，随着实验次数的增加，图像逐渐向右移动，并且峰值逐渐变小。

5.3、二项分布与正态分布

画图代码

def normalpdf(mu,sigma,sample):
    """
    Parameters
    ----------
    mu : float
        正态分布的均值.
    sigma : float
        正态分布标准差.
    sample : int
        生成的样本数量,x轴的最大值.

    Returns
    -------
    x : float
        x轴值.
    probability : float
        取值为x轴值时，对应的概率密度函数值，相当于离散变量的概率.
    """
    mu = mu
    sigma = sigma
    sample = sample
    x = np.arange(sample+1)
    probability=np.exp(-(x-mu)**2/(2*sigma**2))/(math.sqrt(2*math.pi)*sigma)#正态分布的概率密度函数
    return x,probability

n=10
p=0.5
plt.subplot(1,1,1)
mean = n*p#二项分布的均值
sigam = math.sqrt(n*p*(1-p))#二项分布的标准差
max_k=n
k,probability_bp=bpmf(max_k,n,p)
k,probability_no=normalpdf(mean,sigam,max_k)
plt.plot(k,probability_no,"r",label="normal")
plt.plot(k,probability_bp,"g--",label="binomial")
plt.title("Binomial and Normal distribution" + "(n,p="+str(n)+","+str(p)+")")#设置图片标题
plt.xlabel("Number of successes (k)")#设置图片x轴说明
plt.ylabel("probability")#设置图片y轴说明
plt.legend(loc=0)#将图例放在合适的位置，让系统自动查找
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

输出结果

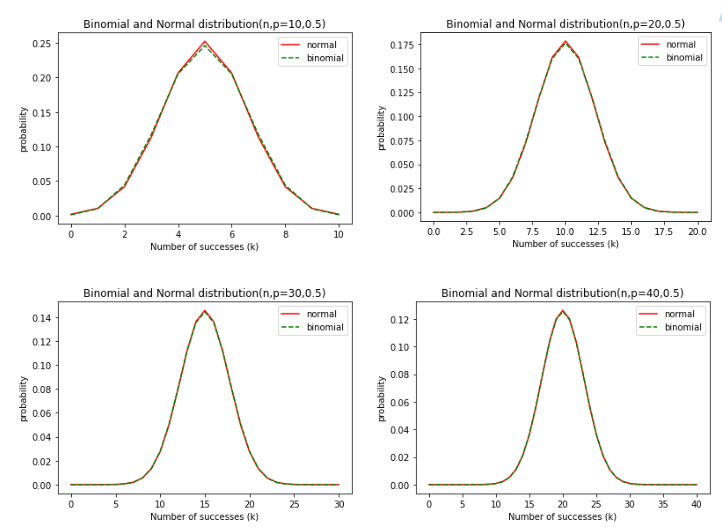
通过图片可以看出，在$p$值不变的情况下，随着试验次数$n$的逐渐变大，二项分布逐渐趋近正态分布。所以在大样本情况下，可以用正态分布近似二项分布。

—End—

*** 参考资料 ***

1、《非寿险精算学》孟生旺著

2、二项分布_百度百科 (baidu.com)

3、二项分布_saltriver的博客-CSDN博客_二项分布

4、二项分布的均值与方差公式的推导 - 知乎