基于级联FFT的广义互相关算法在声源定位中的应用

 

00摘要

  针对2020年第十五届全国大学生智能车竞赛信标组关于声音信标的识别，需要采集声音信号和FM信号，通过声音信号和FM信号互相关进行距离检测和通过两组声音信号互相关进行信标方位判断。

  实际中，是在频域中对两组信号做乘法求最大值，而将时域信号变换为频域信号需要经过FFT变换，本系统引入一种新的级联FFT变换，大大提高了计算速度和效率。为了增加系统的抗干扰性，我们使用了广义互相关算法，有效抑制了噪声和混响的干扰。

  关键词：级联FFT；广义互相关；计算速度；

01引言

  快速傅里叶变换(FFT)本身便是利用了离散傅里叶变换(DFT)中的对称性和周期性，大大缩短了傅里叶变换的时长，这使得FFT成为基本的信号处理算法。

  在2020年第十五届全国智能车竞赛中，信标组的比赛模式发生了很大的变化，从原始的识别一定频率的光信号变为周期性的250~2000Hz的Chirp声音信号和对应的FM调频信号。信标发出的信号的变化导致了信号识别和处理模式的变化，由原来识别光信号使用摄像头，变为接收声音信号的麦克风模块及接收FM信号的FM解调模块，经过不断尝试和选择，麦克风我们使用了9814带自动增益的麦克风模块，FM解调模块使用了RDA5807解调芯片，两者在实际使用中都取得了非常好的效果。

  在信号处理中，一定距离的麦克风接受到的信号进行互相关可以获得声源方位，紧挨着的FM模块和麦克风接受到的信号进行互相关可以得到车身与信标的距离。时域互相关运算计算量是十分庞大，实际上可以看做是两组离散信号的时域卷积运算，因此一般我们会把这种卷积运算转换到频域中，将时域卷积等效为频域相乘，这样会大大简化我们的计算。将时域信号变换到频域一般使用快速傅里叶变换(FFT)，但在实际使用中这种速度仍然无法满足高速定位的需求。我们选用了TC264DA芯片的核心板，与普通TC264D芯片不同，TC264DA拥有512K的EMEM内存空间和内置了硬件FFT计算资源，硬件FFT比软件FFT在速度上有质的提升。但其存在的缺点为硬件FFT只能计算整形数据，会造成一定程度的精度丢失，并且硬件FFT最多只能计算1024个点的，这种精度不能满足本次比赛中信标的识别。在本次比赛中至少要使用2048点的FFT，才能在高速下准确定位。为了解决此问题，我们引入了一种新的级联FFT变换，既使用1024点的硬件FFT又能弥补序列长度不够的缺陷，并在此基础上融合入广义互相关，提升互相关的抗干扰性。

02级联FFT算法

  级联FFT算法的基本思想是把长序列进行分段，类似于把一维数组变为二维数组，然后对行和列分别进行FFT变换，用一定的计算方法将多个短序列的FFT合成原长序列的FFT结果。

  直接把一段C=M×N点序列信号x(n+mN)，n=0,1,2,…,N-1;m=0,1,2,…,M-1;当做一维序列进行FFT变换，运算结果可以表示为：

  把一段C=M×N点序列信号x(n+mN)，n=0,1,2,…,N-1;m=0,1,2,…,M-1;当做二维独立序列进行FFT变换，也就是先进行行方向N点的FFT运算，再进行列方向M点的FFT运算，两者序列编号不相关，运算结果可以表示为：

  当把这段序列看做一维序列排列为二维序列时，序列编号将会发生变化，对应的FFT运算公式也会发生变化，运算结果表示为：

  化简后得：

  可以看出(1-4)和(1-2)只相差e^(-j2πnp/N)，也就是只要使e^{(-j2πnp/N)=1}即可使两者相等，但实际上，e^(-j2πnp/N)不可能一直等于1。

03交叉项补偿

  根据分析，独立的二维序列行和列进行级联FFT运算和一维序列排列成二维序列再进行行和列的级联FFT运算，两者相差一个补偿因子e^(-j2πnp/N)，在实际中，我们只需在中途乘上补偿因子即可使两者等效。

  由FFT运算的线性性质可以得到，矩阵化后的数据进行FFT运算时，行和列运算顺序不同不会影响最终的结果。将两维的运算顺序调换后，也就是先进行列方向的FFT变换，再进行行方向的FFT运算，运算结果可以表示为：

  进行了列变换后，就需要加入补偿因子，运算过程如下：

  化简后得：

  综上，级联FFT具体过程为：首先将一维序列排列为二维序列M行N列，首先对每行进行FFT变换，对每个元素乘以补偿因子e^(-j2πnp/N)，然后对每列进行FFT变换，最后按列取出即为原一维序列FFT变换后的结果。

04.MATLAB仿真

  在本次竞赛中，我们使用了2048点的声音信号做互相关，并在频域相乘之后进行频域补零，补为4096个点，然后使用级联IFFT变换取最大值，即得到互相关最终结果。

  我们采样了一组FM解调信号进行了一系列仿真实验，通过该信号和该信号的延时信号模拟FM和麦克风的互相关运算。首先是使用普通的FFT进行互相关实验，原始FM信号和延迟的FM信号波形图如图D-1所示，两者的普通的FFT变换波形如图D-2所示，互相关结果如图D-3所示，使用MATLAB求互相关结果最大值，最大值点为第201点，设置的延迟为100点，因为在频域中进行了补零操作，所以互相关结果精度是原始点数的两倍，实验结果正确。

^{▲ 普通FFT下FM信号波形和100点延迟的FM信号波形}

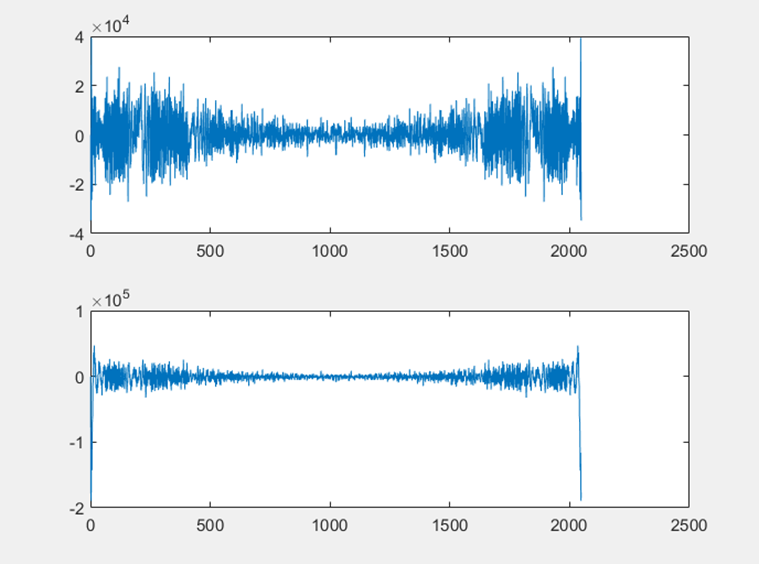
^{▲ 普通FFT下的两信号FFT变换}

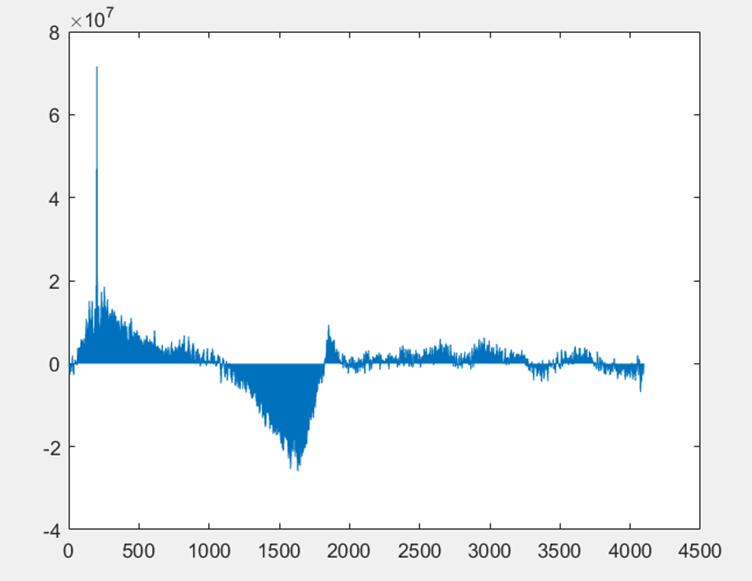
^{▲ 普通FFT下两信号互相关结果}

  同理，我们使用级联FFT，首先把2048点放置为两行1024点，先对列进行两点FFT变换，再对所有点数乘以补偿因子，接着对每行进行1024点的FFT变换，最后按列取出即可。然后进行互相关运算，接着把2048点的结果补零为4096。然后把4096点按列排列为4行1024点，进行级联IFFT运算，级联IFFT可以看做级联FFT的逆运算。运算步骤类似这里不进行展开了。MATLAB仿真结果如下，FM信号和FM延时信号如图D-4所示，两者级联FFT变换如图D-5所示，最终互相关结果如图D-6所示，使用MATLAB求最大值点，对应为第201点

^{▲ 级联FFT下FM信号和100点延时的FM信号波形}

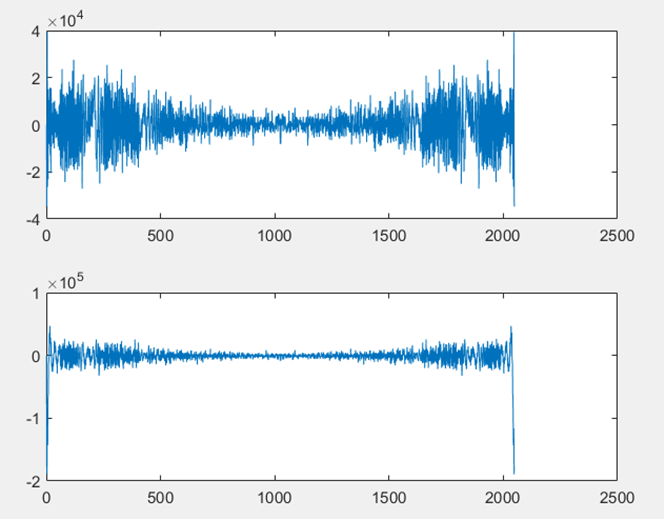
^{▲ 级联FFT下两信号级联FFT变换后的波形}

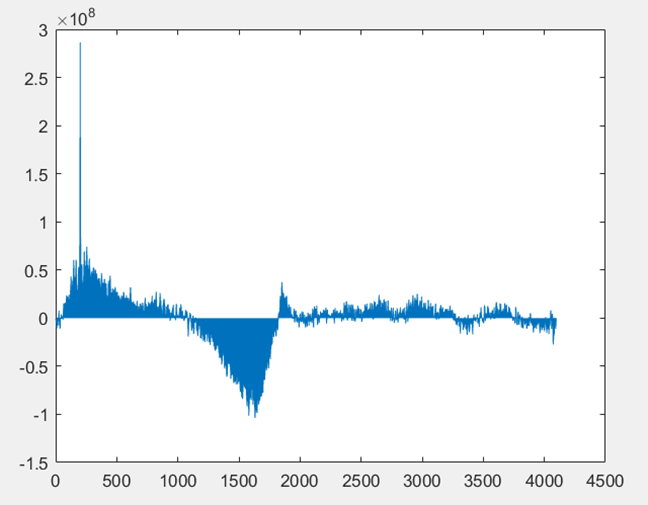
^{▲ 级联FFT下两信号互相关结果}
  从上面结果可以看出，级联FFT运算结果和普通FFT运算结果完全一致，两者是等效的，然而把级联FFT运用到带有硬件FFT的MCU中就可以节省大量的运算时间，把软件运算转化为硬件计算，大大提高了运算速度和运算效率.

05广义互相关

  在实际使用麦克风时，很容易受到轮子噪声，空气中的噪声，以及墙面反射等的影响，这会使接受到的信号产生失真，无论是线性失真还是非线性失真都会给我们的互相关结果带来巨大影响。

  类似于前面所说的基本互相关方法，广义互相关算法估计得到的时延同样对应于两个麦克风接受到的信号之间的相关函取得最大值的位置。

  上面式子中，${\tau }_{12}$是两个信号之间的延时，$G_{x1x2}\left(\omega \right)$是$x_1\left(n\right)$和$x_2\left(n\right)$的互功率谱。$X_1\left(\omega \right)$是$x_1\left(n\right)$的傅里叶变换，$X_2\left(\omega \right)$是$x_2\left(n\right)$的傅里叶变换。

  减弱或消除实际环境中噪声、混响的影响，可以在互功率谱频域中使用加权函数给予一定加权，再经过IFFT变换后得到广义互相关结果，广义互相关函数表达式为：

${\psi }_{12}\left(\omega \right)$为频域加权函数，加权函数不同，实际效果也会有差异，实际应用中，可以针对噪声和混响情况选取不同的加权函数，使相关函数峰值尖锐化，从而使得估计值更加准确。加权函数的选取主要有互功率谱相位（PHAT），ROTH处理器和平滑相干变换（SCOT）。

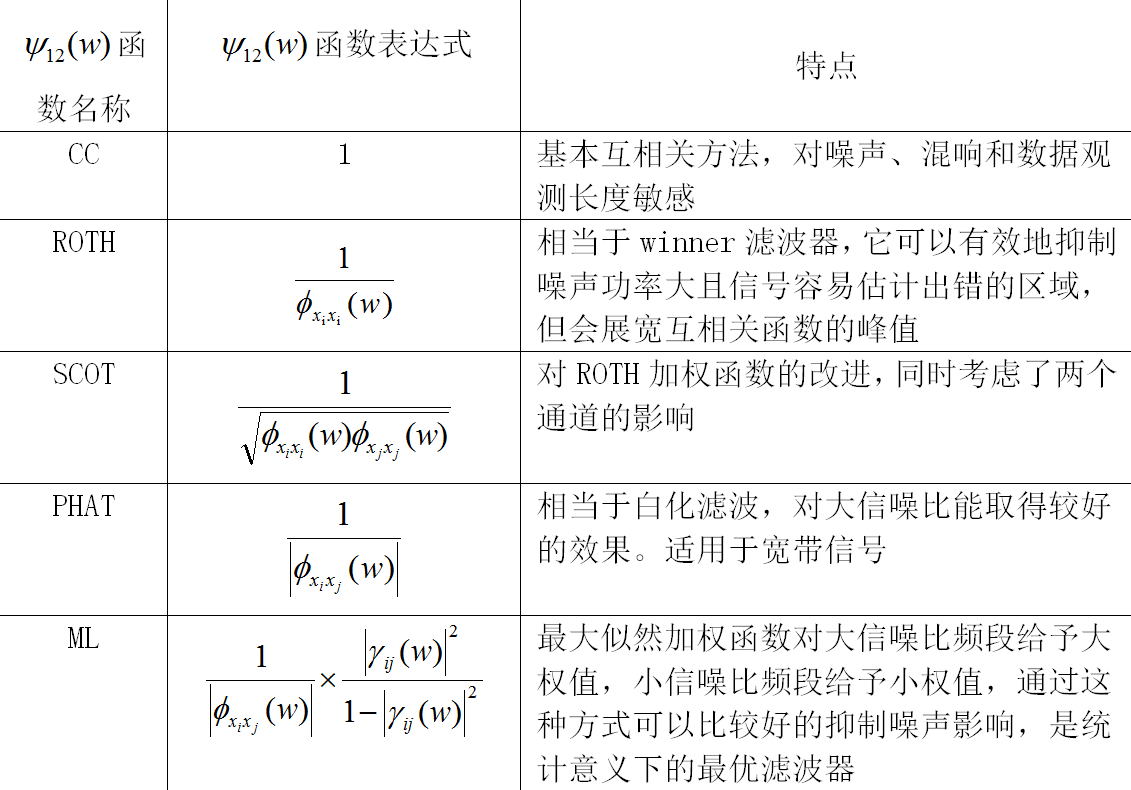
^{▲ 各种加权函数特性分析表格}

上表中， ${\phi }_{x_i{x}_i}\left(\omega \right)$、${\phi }_{x_j{x}_j}\left(\omega \right)$分别表示麦克风信号$x_i\left(n\right)$ 、$x_j\left(n\right)$ 的自功率谱， ${\phi }_{x_i{x}_j}\left(\omega \right)$表示$x_i\left(n\right)$ 和$x_j\left(n\right)$ 的互功率谱， ${\left|{\gamma }_{ij}\left(\omega \right)\right|}^2$定义为如下形式[2]：

  广义互相关原理图如图C-7所示。

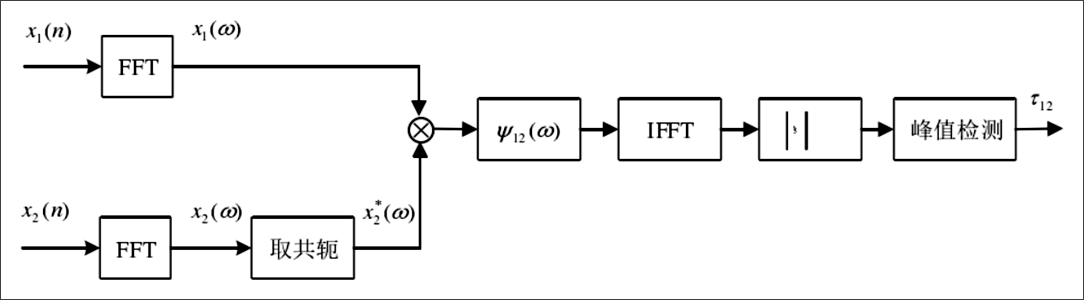
^{▲ 广义互相关原理图}

  由于时间原因，本次备赛中我们只尝试了GCC-PHAT和GCC-ML，其中只有GCC-PHAT试用成功了，GCC-ML还需要进一步研究。使用MATLAB对GCC-PHAT的效果进行仿真验证，FM信号和FM延时100点的信号如图C-8所示，两者级联FFT结果如图C-8所示，在频域相乘时，按照GCC-PHAT的方法要除以互功率谱的模，然后进行级联IFFT，结果如图C-9所示，最后取最大值点，MATLAB比较后最大值点为201。这和前面结果相同，也是符合理论结果的。

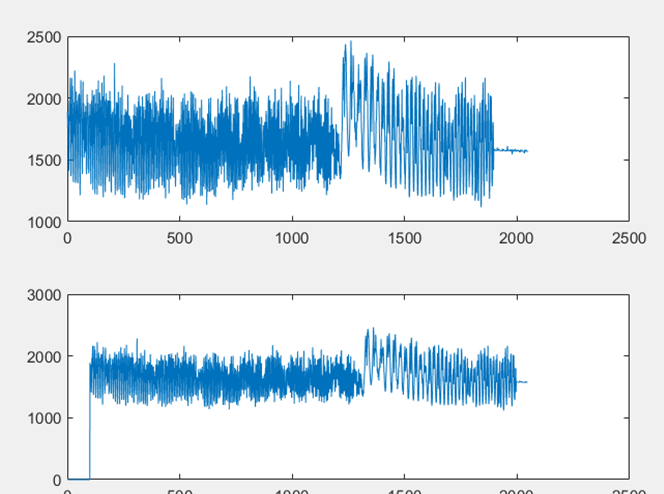
^{▲ 级联FFT下FM信号的100点延时的FM信号波形}

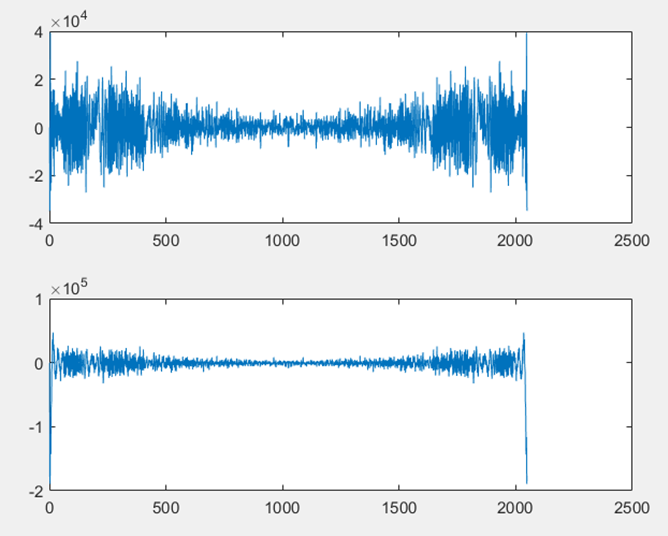
^{▲ 级联FFT下两信号级联FFT变换波形}

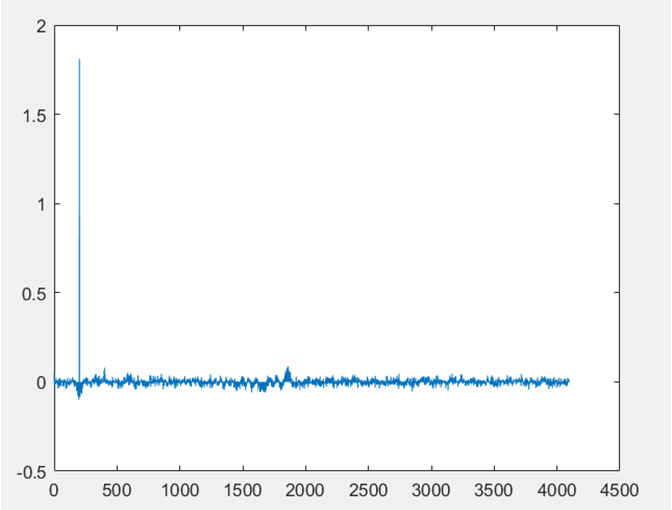
^{▲ 级联FFT下两信号广义互相关后的结果}

  对比图D-6和图D-10，从级联IFFT输出的波形可以看出，相比于普通的互相关，广义互相关的结果最大值以外的波形更加小和平缓，没有很大的尖峰，效果更好，说明广义互相关的确可以减小信号失真的影响。

06.结论

  对序列进行级联FFT变换得到的结果和普通FFT变换得到的结果是完全一致的，仿真结果也说明使用级联FFT代替FFT是没有影响的，级联FFT可以用于互相关运算。广义互相关可以减小系统噪声、混响等的影响，通过MATLAB仿真，比较普通互相关和广义互相关的结果，从图像上可以看出广义互相关的效果确实更好。

  因此，在竞赛中，结合TC264DA芯片的硬件FFT运算资源，级联FFT可以大大减少运算时间，加快系统的响应速度；使用广义互相关可以有效抑制噪声、混响的干扰，提高互相关计算的准确度。

  我们始终相信，信号处理好，开环也能跑 。