算法刷题-二叉树-理论基础(python)

背景：

what？二叉树是树形结构的一个重要类型，最开始了解是数据结构章节中的树

树有很多种类：

        无序树：树中任意节点的子结点之间没有顺序关系，这种树称为无序树,也称为自由树；

        有序树：树中任意节点的子结点之间有顺序关系，这种树称为有序树；

        ：每个节点最多含有两个子树的树称为二叉树；

       满二叉树：叶节点除外的所有节点均含有两个子树的树被称为满二叉树；

       完全二叉树：除最后一层外，所有层都是满节点，且最后一层缺右边连续节点的二叉树称为完全二叉树；

        哈夫曼树（最优二叉树）：带权路径最短的二叉树称为哈夫曼树或最优二叉树。

why？因为二叉树结合了有序数组，链表这两者的优点。在树中查找数据的速度和有序数组中查找一样快。并且插入数据和删除数据的速度和链表一样。

When？

1、哈夫曼编码，来源于哈夫曼树（给定n个权值作为n个叶子结点，构造一棵二叉树，若带权路径长度达到最小，称这样的二叉树为优异二叉树，也称为赫夫曼树(Huffman tree)。即带权路径长度最短的树），在数据压缩上有重要应用，提高了传输的有效性，详见《信息论与编码》。

2、海量数据并发查询，二叉树复杂度是O(K+LgN)。二叉排序树就既有链表的好处，也有数组的好处， 在处理大批量的动态的数据是比较有用。

3、C++ STL中的set/multiset、map，以及Linux虚拟内存的管理，都是通过红黑树去实现的。查找最大（最小）的k个数，红黑树，红黑树中查找/删除/插入，都只需要O(logk)。

4、B-Tree，B+-Tree在文件系统中的目录应用。

5、路由器中的路由搜索引擎。

思路：

how？

1.定义：

class TreeNode:
    def __init__(self, val, left = None, right = None):
        self.val = val
        self.left = left
        self.right = right

2.查找即遍历:首先得判断二叉树不为空

实践：

前序遍历：指的根节点在前，然后左节点右节点依次类推

中序遍历：先是左节点，然后根节点在中，后来右节点依次类推

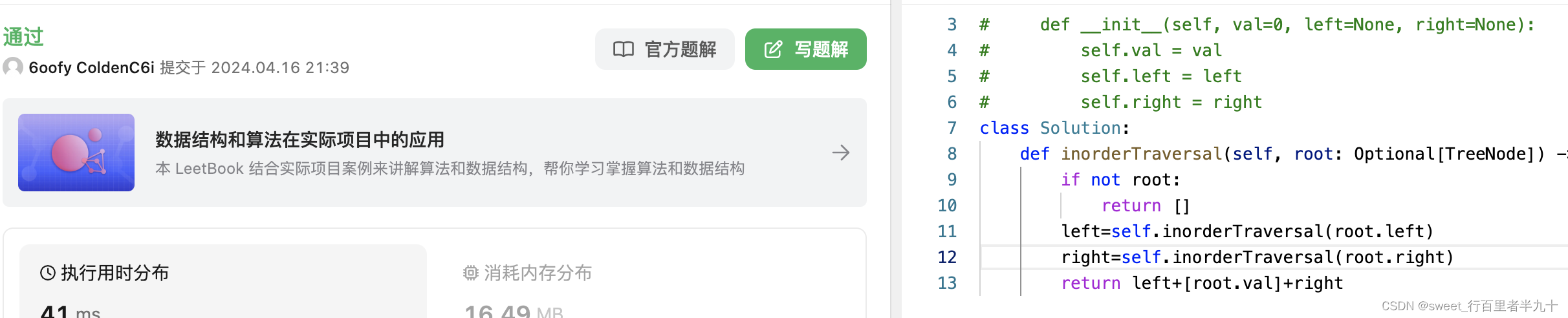
后序遍历：先是左节点，然后右节点，最后根节点，依次类推

复盘：