热门标签
热门文章
- 1Tensorflow 环境配置与安装版本的选择_tensorflow各版本 安装需求
- 2小程序获取不到用户头像和昵称返回微信用户问题解决,即小程序授权获取用户头像规则调整的最新解决方案_微信小程序获取头像加载弹出
- 3平面切分- 蓝桥杯第十一届Python组第九题_平面切分摘要
- 4zabbix配置(三)之mysql监控_怎么查看zabbix的mysql配置
- 5jdk8銝要onematch_JDK8新特性详解 - 纯粹而又极致的光--木九天 - OSCHINA - 中文开源技术交流社区...
- 6无线瘦AP部署——Capwap隧道原理及故障:无线Capwap隧道技术原理_在瘦ap与ac通讯,中,我们规定了capwap的通信方式,那么capwap隧道的建立步骤中几步
- 7一、Docker:Linux/Windows在线安装Docker与命令大全总结_docker for windows installer
- 8洛谷刷题C++语言 | P5705 数字反转_输入一个不小于100且小于1000数字反转c语言
- 9校验输入大于0且可保留小数点后两位数的正则_正则大于0保留两位小数
- 10可信计算3.0工程初步pdf_查校 | 英国大学工业工程与运筹学专业40个授课硕士+研究Mphil/Phd 项目汇总...
当前位置: article > 正文
第四章 图像的频域增强_-dffftkfddx/m
作者:繁依Fanyi0 | 2024-02-12 18:45:36
赞
踩
-dffftkfddx/m
- 傅里叶变换
- 频域变换
• 图像增强除可在空域进行外,也可以在变换域进行。最常用的变换域就是频率域
• 对图像进行傅里叶变换就可转到频率域
• 频域增强有直观的物理意义,增强是通过改变图像中不同频率分量来实现的,而不 是对逐个像素进行的
• 图像频谱给出图像全局的性质,用频率分量来分析增强的原理比空域方便
- 2-D离散傅里叶变换(DFT)的定义

– 一个大小为MxN的图像,DFT以后在频域也是一组MxN的数据,一般而言是一组复数,分别代表原图像在频域的幅频特性和相频特性
– 2-D傅里叶变换基本具有1-D傅里叶变换的性质
• 周期、线性、平移、尺度、共轭对称、微积分、卷积等
• 并具有2-D特有的旋转、可分离等性质
- 2-D离散傅里叶变换的性质
- 空域周期和频域频率:∆u∆x=M ∆v∆y=N
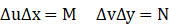
MxN图像大小;
∆x空域--∆u频域 若∆x=2, ∆u=M/2, 表示空间周期为2 的信号,其频域 特性体现在M/2 位置;
若∆u=1, ∆x=M, 表示频域中∆u=1 位置的特性代表空域中以M为周期的信息情况
- 平移性质:

- 周期性质
fx,y=fx+kM,y+lN![]()
Fu,v=F(u+kM,v+lN)![]()
k,l为整数
- 对称性质:对普通情况下的实数图像
– F(u,v)的幅频特性是(u,v)偶函数,相频特性为(u,v)奇函数
– F(u,v)的实数部分是(u,v)偶函数,虚数部分为(u,v)奇函数
- 旋转性质
x = r cosθ, y = r sinθ, u =ωcosϕ, v =ωsinϕ
f(r,θ+θ0)⇔F(ω,ϕ+ϕ0)
- 尺度性质
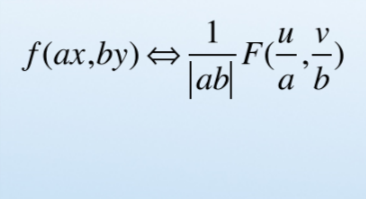
- 卷积性质

- 傅里叶变换相关计算

- 傅里叶变换与相关计算
-特征提取

-图像配准

声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/繁依Fanyi0/article/detail/78384
推荐阅读
相关标签


