论文导读 | 利用GPU的基于图的近似近邻搜索加速研究_基于层次聚类的大规模图近似最近邻搜索

引言

近邻搜索（Nearest Neighbor Search, NNS）是指在一个数据集中寻找与用户查询距离最小的K个数据点。在大多数情况下，数据点被表示为稠密或稀疏向量的形式。数据点之间的距离也有各种各样的定义，常见的距离定义有欧几里得距离、余弦相似度、汉明距离、曼哈顿距离等。通常而言，NNS算法并不关心距离的具体定义，不同的距离定义仅是在计算方面有所不同。NNS具有广泛的应用场景，包括广告、推荐、路径规划等等。

早期的NNS问题主要关注如何设计算法以从数据集中找出与用户查询距离最小的精确解，然而，随着数据规模的增大以及数据形式的复杂化，特别是机器学习与深度学习的快速发展，研究人员使用维数更高的向量对数据进行表示，这时，“维数灾难”（Curse of dimensionality）现象使得精确NNS算法的耗时指数级地增长。有研究表明，精确的NNS算法在处理高维数据时，其性能会退化到与线性搜索同一级别。

幸运的是，人们随后发现，在大数据语境下，绝大部分实际应用并不需要精确解，因此，一系列近似近邻搜索算法（Approximate Nearest Neighbor Search, ANNS）应运而生。近似算法通常会对高维数据进行降维，也避免了在全量数据上进行搜索，大大提高了运行效率。然而，ANNS在面临大数据时代的海量数据时，其能力依然捉襟见肘。因此，除了对算法本身进行改进，研究人员将目光投向了新兴的高性能计算硬件——GPU。借助其强大的并行浮点计算能力，人们能够将ANNS的性能与可扩展性更上一层楼。

背景介绍

首先，本文将简单介绍ANNS的常见类型，以及GPU的架构与特点。

总地来说，ANNS算法可分为三类：基于哈希的方法，基于划分的方法，以及基于图的方法。

基于哈希的方法的中心思想是，利用哈希函数对高维数据进行降维，通过选择恰当的哈希函数，使得降维后得到的哈希码依然维护原来数据中的近似关系。具体而言，基于哈希的方法有两种代表性策略：

其一，是局部敏感哈希（Locality Sensitive Hashing，LSH）。LSH是指一类哈希函数，以原始数据作为输入，输出低维向量或者数值。LSH需要满足的一个重要特性是，两个原始数据点的距离越接近，他们越有可能具有同样的哈希码。一大部分LSH方法在确定哈希函数时，主要考虑距离度量的性质。例如，对于欧几里得距离而言，较为代表性的LSH为线性随机投影（Random linear projections）。

其二，是数据驱动的哈希方式（Learning to hash，L2H）。LSH方法的一个不足是没有考虑数据集的特性，L2H则充分利用了这些特性，从数据中学习满足目标函数的哈希映射。这些目标函数可以包括映射后数据点间的相似度、哈希码的随机性、以及多个哈希函数之间的互相独立等。目前已有一些基于量化的方法（Quantization）取得了不错的效果。利用深度学习技术实现哈希函数的产生与选取是一个比较新的方向。

基于划分的方法是比较经典的一类方法，其主要思路是对数据构成的高维空间进行切分，在搜索过程中，不断通过这些划分缩小搜索空间。基于划分的ANNS主要有三种类型：

其一是基于数据支点的方法（Pivoting），这类方法通常选择某个数据点作为支点（Pivot），根据某种规则对搜索空间进行划分。典型代表为VP-Tree，Ball Tree。VP-Tree选择一个数据点，根据其他点到它的距离进行划分。Ball Tree则是利用超球体进行划分。

其二是基于超平面划分的方法，经典方法如KD-Tree，利用与坐标轴垂直的超平面对数据进行划分。

其三是基于聚合的划分方法，可以通过对数据点做聚类（Clustering）或维诺（Voronoi partition）切分，基于聚合结果中的局部性来确定数据的划分方式。

而基于图的方法是目前搜索性能较好的一类方法，如下图所示，其主要做法是利用原始数据构造一张近似性图（proximity graph），通过在图上寻路的方法不断从一个随机选择的起始点（seed vertex）逼近最终的近似解。基于图的方法也是本文重点关注的类型。

基于图的方法可以根据构建的近似性图的不同分为四类：基于德劳内图（Delaunay Graph）的方法、基于KNN图的方法，基于相对邻接图（Relative Neighborhood Graph， RNG）的方法，以及基于生成树的方法（Spanning Tree）。需要注意的是，虽然近似性图有不同的定义，但是搜索的方法基本上可以说是通用的。主要的搜索策略是束搜索（beam search）。

基于德劳内图的方法将数据点视为图中的结点，构建德劳内图。它的主要缺点是构建非常耗时，并且由于图的连通性非常强，导致其并不能很好地缓解海量高维数据下的维数灾难和性能下降问题。

基于KNN图的方法同样将数据点视为结点，将每个数据点与其K个近似邻居相连，构成KNN图。构建精确KNN图的代价同样很高，目前的主流做法是先随机生成一张KNN图，然后迭代地对其进行优化和修改直到收敛。代表性方式是NN-Descent方法。

基于RNG图的方法与KNN图不同，其构造的相似性图不仅在距离较近的数据点之间连边，在距离较远的数据点之间同样有边。在搜索过程中，这些边类似于一种捷径，使得搜索过程可以更快地收敛。其中的代表性方法有NSW算法和HNSW算法。

基于生成树的方法则顾名思义，利用图的生成树进行NN搜索。但由于图的连通性太差，基于生成树的方法的准确度并不稳定。

---

SONG: Approximate Nearest Neighbor Search on GPU

本文是来自百度的团队发表在ICDE2020上的工作。

本文主要从工业界的实际需求出发，指出ANNS更加适合目前数据量大的应用场景。然而，在对ANNS进行并行化的过程中，查询级别的并行并不能够很好地满足性能需求，一些非常耗时的查询计算没有得到优化。目前的技术方案主要是运行在CPU上，其中，95%的计算代价来自于计算两两数据点之间的距离。而这种两两向量之间的运算非常适合使用GPU硬件来执行。可见，GPU在加速ANNS方面有很大的潜力，但目前针对基于图的ANNS在GPU平台上的加速的研究还相对缺少。为了满足实际需求，填补研究空白，本文作者提出了SONG，SONG主要的关注点在于加速基于图的ANNS中搜索的部分。下图用例子展示了基于图的ANNS中搜索的过程：

在搜索过程中需要维护三个数据结构，其中q为优先队列，用于维护用于在搜索空间中拓展搜索路径的结点。Topk为最大堆，维护的是当前迭代轮次ANNS的结果集。Visited为哈希表或bitmap，维护的是搜索过程中访问过的结点记录。迭代开始前，随机选择了结点1为起点。在第一轮迭代中，结点1进入了topk中，将结点1的邻居2,7,4,5加入了优先队列q中，每个点关联的优先度为该结点到查询点的距离。第二轮迭代中，取q中优先度最低的元素结点2（即离查询距离最短的结点），将其邻居加入到q中。由于这时topk中只有一个元素，所以直接将结点2加入topk中。在第三第四轮迭代中，结点8与结点7相继加入topk中。这时，下一个拓展的结点为结点3，然而，结点3到查询的距离比topk中任一结点到查询点的距离大。这时，由于无法更新topk，算法结束。

系统概要

SONG系统将上述算法全部迁移到了GPU中来运行。如图所示为SONG系统的处理流程梗概。在每轮迭代中，首先将用于拓展的结点（即需要计算距离的结点）从GPU的Global memory中存储的图数据中复制到共享内存中（Candidate Locating），随后，多个GPU中的warp（32个线程）并行地计算这些结点到查询点的距离（Bulk Distance Computation），并将计算得到的结果存到共享内存中。最后，一个warp中的其中一个线程使用计算得到的距离数值修改算法中提到的q，topk，visited三个数据结构。

优化设计

本文分别从数据结构、候选点获取和距离计算三个方面对GPU部分的设计进行优化。

在数据结构方面：

GPU上需要存储的数据/数据结构主要包括：相似性图、优先队列q、最大堆topk、visited数组/哈希表、用户查询等。针对这些数据，本文作者进行了针对性的优化。

第一，针对相似性图的存储与读取，本文作者认为，基于图的ANNS所构建的图结构，要么每个结点都具有相同数量的邻居（KNN图），要么可以在构建过程中限制一个结点邻居数量的上界（RNG图）。因此，在存储时，可以为每个结点预先分配固定大小的空间（Fixed degree graph storage），引入少量的冗余来减少读取邻居信息时的额外开销，并且能够更好地适应Cacheline和存储对齐机制。

第二，在并发控制方面，考虑到每轮迭代中对优先队列q、topk和visited的访存需求较小，SONG分配了一个线程串行地处理这些工作。

第三，在访存方面，系统将查询、候选点集合以及计算得到的距离存储在shared memory中，以提高线程读取的效率。而其余数据结构由于占用空间太大，只能够存放在global memory中。

第四，本文作者在实现visited数据结构时，考虑使用Bloom filter，通过引入少量可接受范围内的false positive误差，大大缩小了visited需要的空间。

第五，为了进一步压缩每轮迭代需要的Global memory访存，本文作者从三个主要的数据结构：优先队列q，topk，以及visited入手进行了优化。对优先队列q，本文作者发现，如果一个结点在进入优先队列q时，队列中已经存在了k个比它距离更近的点，那么在以后的所有迭代中，它都不会被加入到topk中，换而言之，优先队列q的容量可以限制为K。另外，在优化前的算法中，Visited会维护每一个点的访问历史，但因为在GPU上的计算非常快但访存相对较慢，所以可以通过允许一部分重复访问和距离计算，进一步压缩Visted所需的空间。这时对Visited不仅要进行插入，而且要进行删除。Bloom filter并不能支持插入数据的删除。本文作者认为Cockoo filter是一个更好的选择。

在候选点获取方面：

进行候选点获取时，GPU中的线程从相似形图中将未被访问过的，需要进行距离计算的数据点索复制到本地。这时，一种可行的优化是，令一个Warp中的多个线程并发地取回不同query所需的候选点，以提高并行度。同时，由于相似性图中一个点的邻居数量往往是有限的，即每次取一个点的邻居时，能取回的数据较少，浪费了GPU上的并行计算能力，因此可以同时取多个点的邻居作为候选点。

在距离计算方面：

本文作者分析了两种不同的线程分配方式。一是分配一个线程处理一组距离的计算，同时进行多组距离计算。一是分配多个线程处理同一组距离的计算，每个线程负责一部分的计算任务。作者认为，后者能够更好地利用GPU中访存合并的特性，因为计算所需的数据点并不一定是在Global memory上连续存储的，但同一个数据点的内容一定是连续存储的。所以第二种计算方式的访存代价更低。

最后，本文作者还讨论了SONG系统如何应对GPU的Global memory不足以存下所有数据时的问题。在优化前的系统中，Global memory中主要需要存储的是原始的向量数据与相似性图。由于相似性图的度数有上限，因此占用的存储空间相对较小。本文作者提出，可以使用一种基于哈希的方法对数据进行降维。与LSH类似，通过h个从高斯分布中得到的随机的向量，将h个向量内积作为输入，通过一组哈希函数得到一个h位的bitmap，从而对原向量进行降维。

实验

下图是实验中使用的数据集：

在与其他算法的比较中，SONG有较大的优势。HNSW是目前在CPU上运行搜索效率较高的算法，Faiss则是此前在GPU上ANNS的SOTA。

  

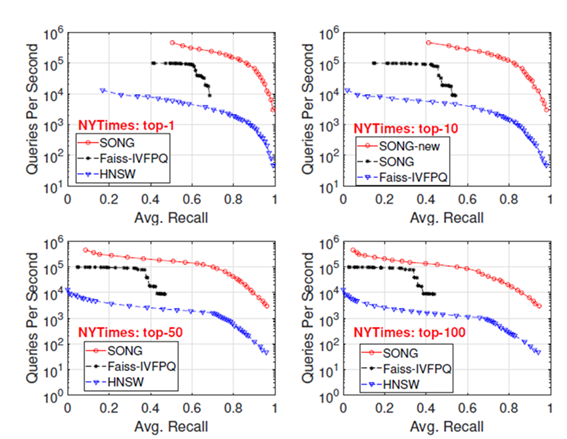
如图所示，与CPU上的HNSW相比，SONG将ANNS的性能近两个数量级。而与GPU上的系统Faiss相比，它同样有大约10倍的提升。

---

Fast k-NN graph construction by GPU based NN-Descent

另一篇文章则是来自于湖南大学的研究团队发表在CIKM2021上的工作。上一篇文章主要关注ANNS中搜索过程的加速，而本文则关注相似性图的构建的加速。具体地说，是对KNN图的构建过程的加速。本文作者分析了目前主流的近似KNN构图方式NN-Descent，利用GPU硬件对其进行加速。

系统概要

NN-Descent算法的中心思想是随机地初始化KNN图，然后在多轮迭代中不断对其进行修改，直到收敛。算法的具体流程如下所示。

NN-Descent的流程主要可以分为四个步骤。首先，对数据集中每一个数据点，为其随机初始化K个KNN近邻，然后开始迭代过程。每个数据点有两种可能的标签，分别为NEW和OLD。在迭代开始之前，所有的数据点的标签都是NEW。而在迭代过程中，上一步被使用到的结点则会被标记为OLD。迭代过程开始后，在每一轮迭代步内，首先从标签为NEW和OLD的两个集合中随机抽取出一些数据点（Sampling on close neighbors），随后，计算采样的NEW集合数据点之间，以及NEW和OLD数据点之间的相互距离

（Cross matching on sampled neighbors），用于更新这些点的KNN邻居列表（KNN graph update）。

优化设计

将NN-Descent问题迁移到GPU上进行计算的一大障碍在于，难以预测每一轮迭代中NEW与OLD集合中的数据点个数，同时也难以预测每轮迭代中实际需要进行更新的次数。这些都为并行计算中的同步与负载均衡造成了麻烦。而在文章中，针对这一挑战，作者强制规定了NEW与OLD集合的大小不能够超过一个给定的阈值。如此虽然一定程度上降低了可靠性，但得益于GPU强大的计算能力，最终性能受到的影响并不大。不仅如此，作者还在NEW和OLD采样的基础上加入了反向邻居的信息。即，若数据点v出现在数据点s的NEW采样集合中，那么也将s加入到v的NEW采样集合中。所有的采样集合都经过去重与排序，方便后续的运算。

在距离计算方面，该系统采取了较为经典的基于tile划分的距离计算方式，如下所示。将计算距离所需的一部分数据（tile）加载到shared memory中，由多个线程分别负责一部分距离数值的计算，最后再对结果进行聚合得到最终输出。

在KNN图更新方面，对图的存储的一种常见的、空间高效的做法是将图表示为一组邻接列表，将邻接列表连续存储。当需要对KNN图的大量修改时，虽然这种存储格式下可以回避重新分配空间的问题，但仍然会产生大量随机的Global memory 访存，同时由于不同线程可能都需要对同一个列表进行修改，并发控制问题同样需要考虑。本文作者的应对策略是，其一，尽量减少每轮需要更新的次数，在三类Cross match中（NEW-NEW, NEW-OLD, OLD-NEW），仅保留每组中距离最近的一组距离进行更新。其二，为每个KNN列表分配固定的内存对齐的存储空间（注意KNN图中的K值并不一定要等于KNN查询中的K值），并将其细分成多个块，为每一个块加上自旋锁。

最后，针对需要聚合多个数据子集得到的KNN图的情况，本文作者提供了一种基于Graph Merge的方法。如下图中算法所示，中心思想是将待合并的两个图一分为二。一半作为NN-Descent的初始KNN图，另一半作为采样集合，对图进行迭代修改直到收敛。这一方法同样能与图分割的方法结合，用于处理大规模的无法在GPU的Global memory中存储的数据集。

 

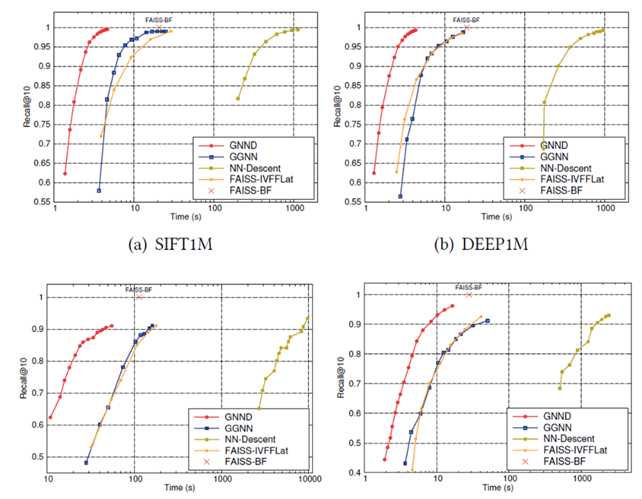
实验

从实验结果来看，在中等规模的数据集中，本文提出的GNND方法与基于CPU实现的NN-Descent baseline、基于GPU的Faiss和GGNN相比均有较大的性能上的优势。在较大规模的数据集中，特别是十亿级别的数据集中，展示出了较大的优势。