主成分分析

一、原理分析

1、主成分分析概述

主成分分析（PrincipalComponent Analysis，PCA）， 将 多个变量通过 线性变换以选出较少 个数重要变量的一种多元统计分析方法。

主成分：由原始指标综合形成的几个 新指标。依据主成分所含信息量的大小成为第一主成分，第二主成分等等。

2、主成分与原始变量之间的关系：

（1）主成分保留了原始变量绝大多数信息。
（2）主成分的个数大大少于原始变量的数目。
（3）各个主成分之间互不相关。
（4）每个主成分都是原始变量的线性组合。

3、思考几个问题

主成分分析就是设法将原来众多具有一定相关性的变量(如p个变量)，重新组合成一组新的相互无关的综合变量来 代替原来变量。 怎么代替?

通常数学上的处理就是将原来p个变量作线性组合作为 新的综合变量。 如何选择?

如果将选取的第一个线性组合即第一个综合变量记为F1，自然希望 F1尽可能多的反映原来变量的信息。 怎样反映?

最经典的方法就是用方差来表达，即var(F1)越大，表示F1包含的信息越多。因此在所有的线性组合中所选取的F1应该是方差最大的，故称之为第一主成分(principal component) 。

F1=ax+by（a，b为未知常数）就是其中的一条关系式，F1就是其中的一个主成分，称为第一主成分（方差最大，尽可能包含所有数据关系）若80%以上数据关系能用他表示，则够了。如果少于%80，可以多写第二主成分 F2=cx+dy（c，d为未知常数）。

并且F1已有的信息就不再出现在F2中，主成分之间互不相关，方差依次递减，F1和 F2，F3.......Fn间没有关系，

如果不够，还可以有第3第4......第n主成分，累计方差贡献率大于80%即可，这个值越大越好。越大表示关系越强。

累计方差贡献率：是所有公因子引起的变异占总变异比例。

假设我们所讨论的实际问题中，有p个指标，我们把这p个指标看作p个随机变量，记为X1，X2，…，Xp，主成分分析就是要把这p个指标的问题，转变为讨论p个指标的线性组合的问题，而这些新的指标F1，F2，…，Fk(k≤p），按照保留主要信息量的原则充分反映原指标的信息，并且相互独立。
这种由讨论多个指标降为少数几个综合指标的过程在数学上就叫做降维。主成分分析通常的做法是，寻求原指标的线性组合Fi。

二、分析案例：

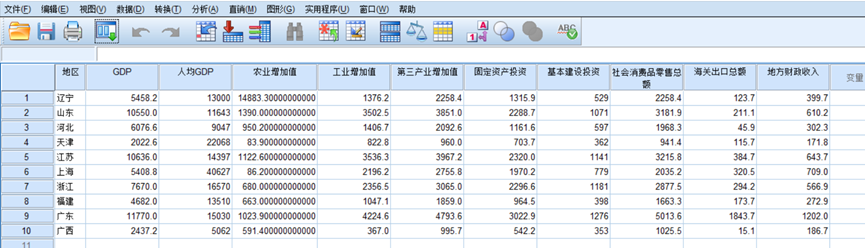
1.数据统一标准化

因为我们得到的原始数据大小,类型不一, 一起分析会不准确, 所以将数据全部标准化到[-10,10]的范围内

选择 分析--描述统计--描述

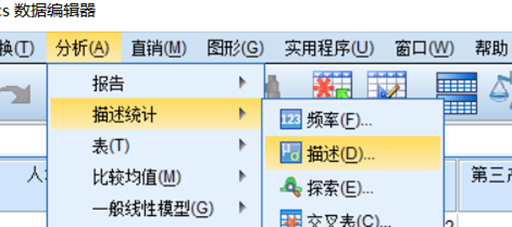
将变量都放入右侧, 并选中将标准化值另存为变量,点击确定

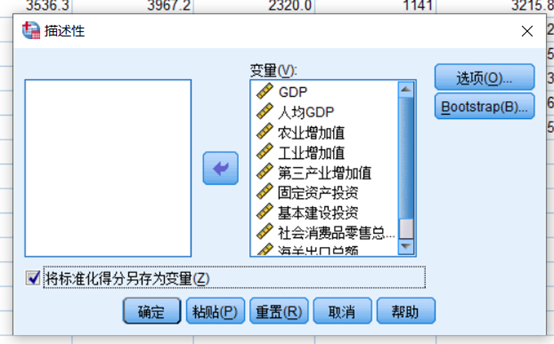
后面以Z开头的都是各变量标准化之后的值, 可以发现所有的变量都在[-10, 10]范围内

2.因子分析

选择 分析--降维--因子分析 并将标准化之后的值全部选中,原始值不要选

描述: 选中 原始分析结果和KMO和巴特利特球形度检验

提取: 选择 协方差矩阵和碎石图

得分: 选择保存为变量

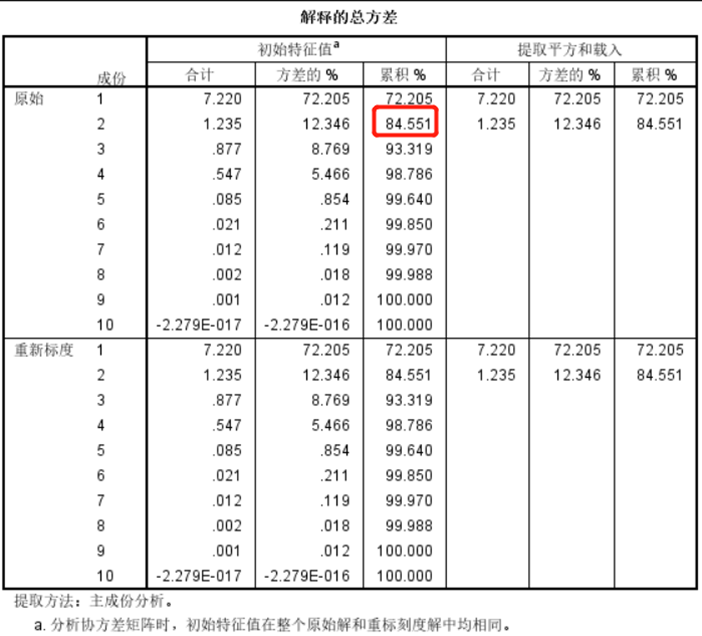
关注 总方差解释, 可以发现前两个变量就占了84%多的影响度(一般占到80%以上即可), 所以可以用前两个变量代替其他的变量

也可以通过碎石图表示

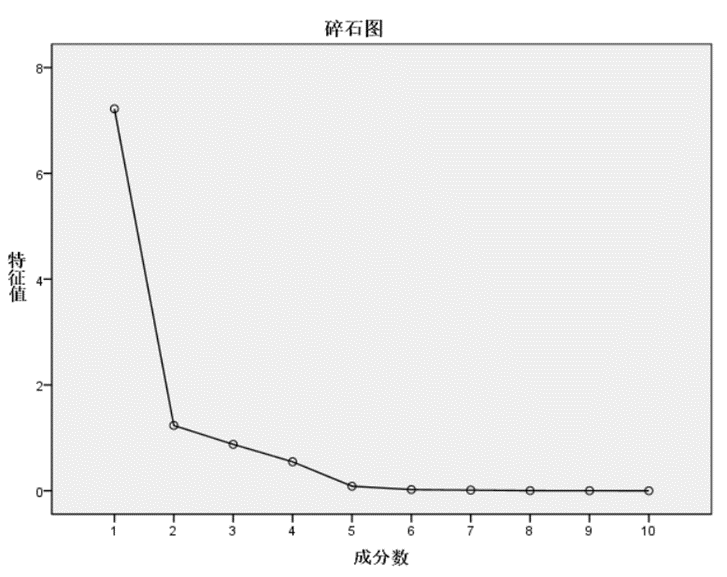
成分矩阵表示 各个主成分与各个因素之间的关系有多大

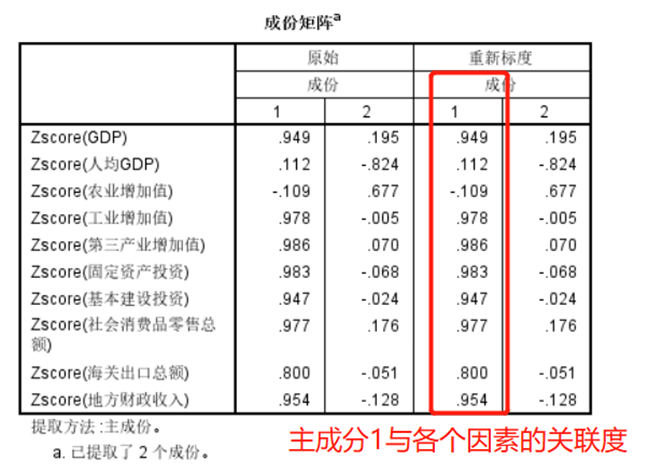
将成分矩阵的重新标度成分, 复制粘贴到变量中, 变成一个新变量,分别记为V1, V2

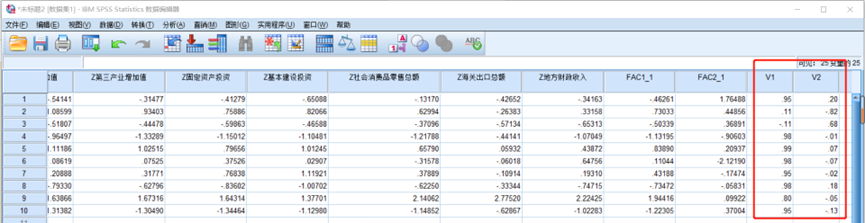
3.转换得到主成分分析的系数

因为spss中只有因子分析, 所以还需要对因子分析的系数做处理才能得到主成分分析的系数
它们之间的关系是 因子分析的系数 / sqrt(特征值) = 主成分分析的系数
特征值就是总方差解释中的总计
然后在 转换--计算变量中可以进行相关计算

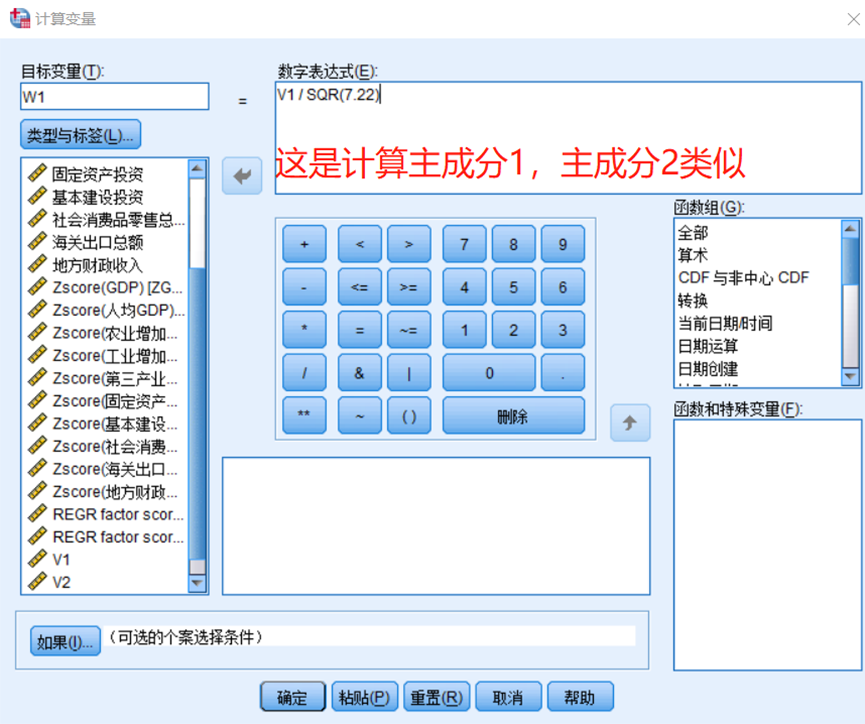
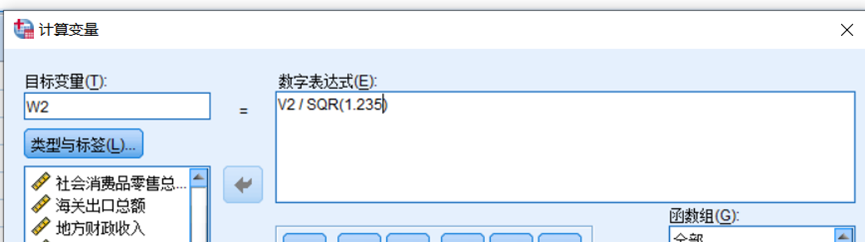
求指标对应的系数

F1=0.353ZX1+0.042ZX2- 0.041ZX3 +0.364ZX4 +0.367ZX5 +0.366ZX6 +0.352ZX7 +0.364ZX8+0.298ZX9+0.355ZX10
F2 =0.175ZX1 -0.741ZX2+0.609ZX3 - 0.004ZX4 +0.063ZX5- 0.061ZX6 - 0.022ZX7 +0.158ZX8 -0.046ZX9 -0.115ZX10

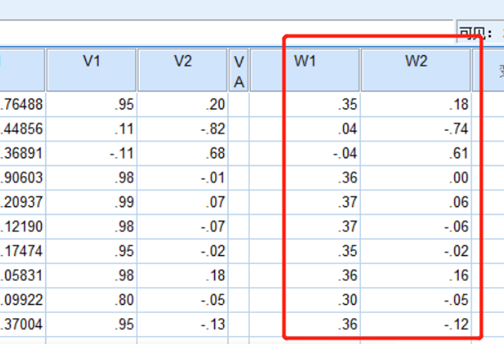
然后再把 主成分分析的系数与原始值标准化之后的值对应相乘, 分别得到最终结果F1, F2
也是在 转换--计算变量中计算

最后, 10个因素降维成只剩下F1, F2两个因素了, 处理问题简化了很多

F=(72.2/84.5) F1+(12.3/84.5) F2

参考资料：

(2条消息) 主成分分析法(数学建模)教授先生_主成分分析法模型_教授先生的博客-CSDN博客