- 1RISC-V单周期处理器设计(指令和控制器)(二)_基于riscv指令集的单周期处理器
- 2OMACP功能说明以及自己做的一个模拟发送OMACP消息的功能类
- 3Oracle的分页、排序、效率问题_oracle rownumber over效率问题
- 4脚手架搭建微信小程序项目_cli3构建微信小程序
- 5【robots.txt】设置网站不允许被搜索引擎抓取的代码_禁止蜘蛛抓取的代码
- 6uniapp 标签打印 笔记_uniapp打印标签
- 7maven中profile的使用详解_maven profile
- 8notebook显示pyecharts画地图_".add(\"商家a\", [list(z) for z in zip(faker.provinc
- 9VUE3 + TS 使用 Axios(copy可直接使用)_ts对axios响应结果进行处理
- 10webvtt_使用WebVTT章节创建交互式HTML5视频
最小二乘法_最小二乘法误差
赞
踩
最小二乘法说白了就是最小平方法,最小二乘法到底是怎么一回事呢?
网上找了很多资料,对最小二乘法也有了一些认识
最小二乘法是一种数学优化技术,其通过最小化误差的平方和寻找数据的最佳函数匹配;利用最小二乘法可以简便的求得未知的数据,并使得这些求得得数据与实际数据之间误差的平方和最小。
简而言之,最小二乘法和梯度下降法类似,都是一种求解无约束最优化问题的常用方法,并也可以用于曲线拟合,来解决回归问题。
一、简单理解二乘法
比如采样获取到一批样本, ( x 1 , y 1 ) (x_1,y_1) (x1,y1), ( x 2 , y 2 ) (x_2,y_2) (x2,y2)… ( x n , y n ) (x_n,y_n) (xn,yn),得到这批数据之后,接下来要处理这堆数据,假设 y y y跟 x x x呈线性关系,即 y = β 0 + β 1 x y=\beta_0+\beta_1x y=β0+β1x,接下来所需要做的就是根据采样获得的数据来求解 β 0 \beta_0 β0和 β 1 \beta_1 β1了。
二、最小二乘法的误差
假设有五个尺子测量同一个线段,会得到五个不同的值10.2,10.3,9.8,9.9,9.8,之所以出现不同值的原因可能是尺子材质不一样;厂家生产的精度不一样等等…总之就是会产生误差,而一般在这种情况,会取平均值作为最终线段的长度,即 x ‾ = 10.2 + 10.3 + 9.8 + 9.9 + 9.8 5 = 10 \overline{x}=\frac{10.2+10.3+9.8+9.9+9.8}{5}=10 x=510.2+10.3+9.8+9.9+9.8=10,但是为什么一定要用 x ‾ \overline{x} x呢,用中位数不行吗,用调和平均数不行吗?下面我们来思考一下这个问题。
如图,将这五个点画入坐标系中,记作
y
i
y_i
yi,其次把要猜测的真实值用平行于横轴的直线表示(虚线表示),这个
y
y
y是用
y
=
β
0
+
β
1
x
y=\beta_0+\beta_1x
y=β0+β1x算出来的猜测值,记作
y
y
y,每个点都向
y
y
y做垂线,每一段垂线的长度是
∣
y
i
−
y
∣
|y_i-y|
∣yi−y∣,也就是真实值和测量值之间的误差,因为误差是长度,且计算起来很麻烦,所以干脆就会用平方和来代表误差:
∣
y
i
−
y
∣
→
(
y
i
−
y
)
2
|y_i-y|\rightarrow(y_i-y)^2
∣yi−y∣→(yi−y)2
由此,误差用数学公式表示就是:
Q
=
∑
i
=
1
n
(
y
−
y
i
)
2
Q=\sum_{i=1}^n(y-y_i)^2
Q=i=1∑n(y−yi)2
由于
y
y
y是猜测的,故可以不断变换,同时
Q
Q
Q也会不断变化

知道误差的表示之后,让总的误差最小的
y
y
y就是真值,这是基于,如果误差是随机的,应该围绕真值上下波动。
即
Q
=
m
i
n
∑
i
=
1
n
(
y
−
y
i
)
2
Q=min\sum_{i=1}^n(y-y_i)^2
Q=min∑i=1n(y−yi)2求这个就好求了;
一般套路:求导
→
\rightarrow
→导数为0
→
\rightarrow
→求出来的
y
y
y就是真值
d
Q
d
y
=
d
d
y
∑
i
=
1
n
(
y
i
−
y
)
2
=
2
∑
i
=
1
n
(
y
i
−
y
)
\frac{dQ}{dy}=\frac{d}{dy}\sum_{i=1}^n(y_i-y)^2=2\sum_{i=1}^n(y_i-y)
dydQ=dydi=1∑n(yi−y)2=2i=1∑n(yi−y)
=
2
[
(
y
1
−
y
)
+
(
y
2
−
y
)
+
(
y
3
−
y
)
+
(
y
4
−
y
+
(
y
5
−
y
)
]
=
0
=2[(y_1-y)+(y_2-y)+(y_3-y)+(y_4-y+(y_5-y)]=0
=2[(y1−y)+(y2−y)+(y3−y)+(y4−y+(y5−y)]=0
y
=
y
1
+
y
2
+
.
.
.
y
5
5
y=\frac{y_1+y_2+...y_5}{5}
y=5y1+y2+...y5求出来的y正好是平均数,原来算数平均数可以让误差最小啊,那看来选它也不无道理。
需要注意的是,误差的分布是一个正态分布,为什么呢?
假设直线对于坐标
x
i
x_i
xi 给出的预测
f
(
x
i
)
f(x_i)
f(xi) 是最靠谱的预测,所有纵坐标偏离
f
(
x
i
)
f(x_i)
f(xi) 的那些数据点都含有噪音,是噪音使得它们偏离了完美的一条直线,一个合理的假设就是偏离路线越远的概率越小,具体小多少,可以用一个正态分布曲线来模拟,这个分布曲线以直线对
x
i
x_i
xi 给出的预测
f
(
x
i
)
f(x_i)
f(xi) 为中心,实际纵坐标为
y
i
y_i
yi 的点
(
x
i
,
y
i
)
(x_i, y_i)
(xi,yi)发生的概率就正比于
e
[
−
(
Δ
y
i
)
2
]
e^{[-(Δy_i)^2]}
e[−(Δyi)2],这也就是误差分布服从正态分布的原因所在了。
在解决第一个问题之后,我们来思考下一个问题,根据采样得到的数据,该怎么求得参数
β
0
\beta_0
β0和
β
1
\beta_1
β1呢
三、最小二乘法的求解
知道了前面的cost function之后,下面的求解过程就很简单了
样本的回归方程为:
Q
=
∑
i
=
1
n
(
y
i
−
β
0
−
β
1
x
i
)
Q=\sum_{i=1}^n(y_i- \beta_0-\beta_1x_i)
Q=i=1∑n(yi−β0−β1xi)
现在需要确定
β
0
\beta_0
β0和
β
1
\beta_1
β1来使得cost function最小,即
m
i
n
Q
minQ
minQ,所以依旧是那几步求解过程:求导
→
\rightarrow
→(偏)导数为0
→
\rightarrow
→求出
β
0
\beta_0
β0,
β
1
\beta_1
β1
具体过程如下:
∂
Q
∂
β
0
=
2
∑
i
=
1
n
(
y
i
−
β
0
−
β
1
x
i
)
(
−
1
)
=
0
\frac{\partial{Q}}{\partial{\beta_0}}=2\sum_{i=1}^n(y_i-\beta_0-\beta_1x_i)(-1)=0
∂β0∂Q=2i=1∑n(yi−β0−β1xi)(−1)=0
∂
Q
∂
β
1
=
2
∑
i
=
1
n
(
y
i
−
β
0
−
β
1
x
i
)
(
−
x
i
)
=
0
\frac{\partial{Q}}{\partial{\beta_1}}=2\sum_{i=1}^n(y_i-\beta_0-\beta_1x_i)(-x_i)=0
∂β1∂Q=2i=1∑n(yi−β0−β1xi)(−xi)=0
将这两个方程整理一下,应用克莱姆法则即可求解出来,鉴于初学者可能有的不知道克莱姆法则,可以看一下克莱姆法则(用这个求解要求
D
≠
0
D\not=0
D=0)
D
=
∣
n
∑
i
=
1
n
x
i
∑
i
=
1
n
x
i
∑
i
=
1
n
x
i
2
∣
=
n
∑
i
=
1
n
x
i
2
−
(
∑
i
=
1
n
x
i
)
2
D=\left|
D
1
=
∣
∑
i
=
1
n
y
i
∑
i
=
1
n
x
i
∑
i
=
1
n
x
i
y
i
∑
i
=
1
n
x
i
2
∣
=
∑
i
=
1
n
x
i
2
y
i
−
∑
i
=
1
n
x
i
∑
i
=
1
n
x
i
y
i
D_1=\left|
D
2
=
∣
n
∑
i
=
1
n
y
i
∑
i
=
1
n
x
i
∑
i
=
1
n
x
i
y
i
∣
=
n
∑
i
=
1
n
x
i
y
i
−
∑
i
=
1
n
x
i
y
i
D_2=\left|
β
0
=
D
1
D
=
∑
i
=
1
n
x
i
2
y
i
−
∑
i
=
1
n
x
i
∑
i
=
1
n
x
i
y
i
n
∑
i
=
1
n
x
i
2
−
(
∑
i
=
1
n
x
i
)
2
\beta_0=\frac{D1}{D}=\frac{\sum_{i=1}^nx_i^2y_i -\sum_{i=1}^nx_i \sum_{i=1}^nx_iy_i}{n\sum_{i=1}^n x_i^2-(\sum_{i=1}^nx_i)^2}
β0=DD1=n∑i=1nxi2−(∑i=1nxi)2∑i=1nxi2yi−∑i=1nxi∑i=1nxiyi
β
1
=
D
2
D
=
n
∑
i
=
1
n
x
i
2
−
(
∑
i
=
1
n
x
i
)
2
n
∑
i
=
1
n
x
i
2
−
(
∑
i
=
1
n
x
i
)
2
\beta_1=\frac{D2}{D}=\frac{n \sum_{i=1}^n x_i^2-(\sum_{i=1}^nx_i)^2}{n\sum_{i=1}^n x_i^2-(\sum_{i=1}^nx_i)^2}
β1=DD2=n∑i=1nxi2−(∑i=1nxi)2n∑i=1nxi2−(∑i=1nxi)2
根据这个公式,就可求解出对应的参数。
四、推广到矩阵形式
假设一个样本有更多的特征,也就是一个样本会有多个模型变量,(注:这里面表示样本用
x
1
,
x
2
.
.
.
x
n
x_1,x_2...x_n
x1,x2...xn,表示多个特征(模型变量)用
x
1
,
x
2
.
.
.
x
n
x^1,x^2...x^n
x1,x2...xn
在一个样本里,可以用如下线性函数表示:
y
=
β
0
+
β
1
x
1
+
β
2
x
2
+
.
.
.
+
β
m
x
m
y=\beta_0+\beta_1x^1+\beta_2x^2+...+\beta_mx^m
y=β0+β1x1+β2x2+...+βmxm
而对于n个样本来说,可以用如下线性方程组表示:
β
0
+
β
1
x
1
1
+
β
2
x
1
2
+
.
.
.
+
β
m
x
1
m
=
y
1
\beta_0+\beta_1x_1^1+\beta_2x_1^2+...+\beta_mx_1^m=y_1
β0+β1x11+β2x12+...+βmx1m=y1
β
0
+
β
1
x
2
1
+
β
2
x
2
2
+
.
.
.
+
β
m
x
2
m
=
y
2
\beta_0+\beta_1x_2^1+\beta_2x_2^2+...+\beta_mx_2^m=y_2
β0+β1x21+β2x22+...+βmx2m=y2
β
0
+
β
1
x
3
1
+
β
2
x
3
2
+
.
.
.
+
β
m
x
3
m
=
y
3
\beta_0+\beta_1x_3^1+\beta_2x_3^2+...+\beta_mx_3^m=y_3
β0+β1x31+β2x32+...+βmx3m=y3
…
β
0
+
β
1
x
n
1
+
β
2
x
n
2
+
.
.
.
+
β
m
x
n
m
=
y
n
\beta_0+\beta_1x_n^1+\beta_2x_n^2+...+\beta_mx_n^m=y_n
β0+β1xn1+β2xn2+...+βmxnm=yn
上述线性方程组可以表示为为:
[
1
x
1
(
1
)
x
1
(
2
)
⋯
x
1
(
m
)
1
x
2
(
1
)
x
2
(
2
)
⋯
x
2
(
m
)
⋮
⋮
⋮
⋱
⋮
1
x
n
(
1
)
x
n
(
2
)
⋯
x
n
(
m
)
]
.
[
β
0
β
1
⋯
β
m
]
=
[
y
0
y
1
⋯
y
n
]
将样本矩阵
x
i
j
x_i^j
xij记为矩阵A,将参数记为向量
β
\beta
β,将真实值记为向量
Y
Y
Y
即
A
β
=
Y
A\beta=Y
Aβ=Y
对于最小二乘法来说,最终矩阵表达形式可记为
m
i
n
∣
∣
A
β
−
Y
∣
∣
2
min||A\beta-Y||_2
min∣∣Aβ−Y∣∣2
最后的最优解即为:
β
=
(
A
T
A
)
−
1
A
T
Y
\beta=(A^TA)^{-1}A^TY
β=(ATA)−1ATY
方程解法如下:

其中倒数第二行中的中间两项为标量,所以二者相等。然后利用该式对向量
β
\beta
β求导:
 由矩阵的求导法则:
由矩阵的求导法则:

可知该式的结果为:

令上式结果=0可得:
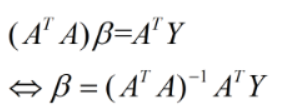
即为最小二乘法的解析解,它是一个全局最优解。
五、最小二乘法的改进
经典的最小二乘法使用起来足够简单粗暴,其考虑了每个样本的贡献,即每个样本具有相同的权重,但是有一个问题就是对噪声的容忍度很低(很敏感),即使得他对异常点比较敏感,因此提出了加权最小二乘法,相当于给每个样本设置了一个权重,以此来反映样本的重要程度或者是对解的影响程度。


