分类3：机器学习处理read-wine（红酒）数据集代码_wine数据集

1 介绍

红酒分类数据集属于分类问题，共有13个特征，类别共有10个，因此属于分类问题，我们使用svm、knn、决策树、随机森林等方法对其进行分析，本文还包含PCA降维、数据可视化、超参数、数据归一化等操作，代码可以直接跑通。
数据集连接：
链接：https://pan.baidu.com/s/1mncFxgyGQY9165AdvIFKCg?pwd=4chf
提取码：4chf

2 导入常用的工具箱

import pandas as pd
import numpy as np
from sklearn.decomposition import PCA
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler,MinMaxScaler
np.random.seed(123)
1
2
3
4
5
6
7
8
9
10
11
12

3 导入数据集

导入数据集，并且完成简单的数据可视化操作

data = pd.read_csv("winequality-red.csv")
print(data.describe())

data.hist()
plt.show()
1
2
3
4
5

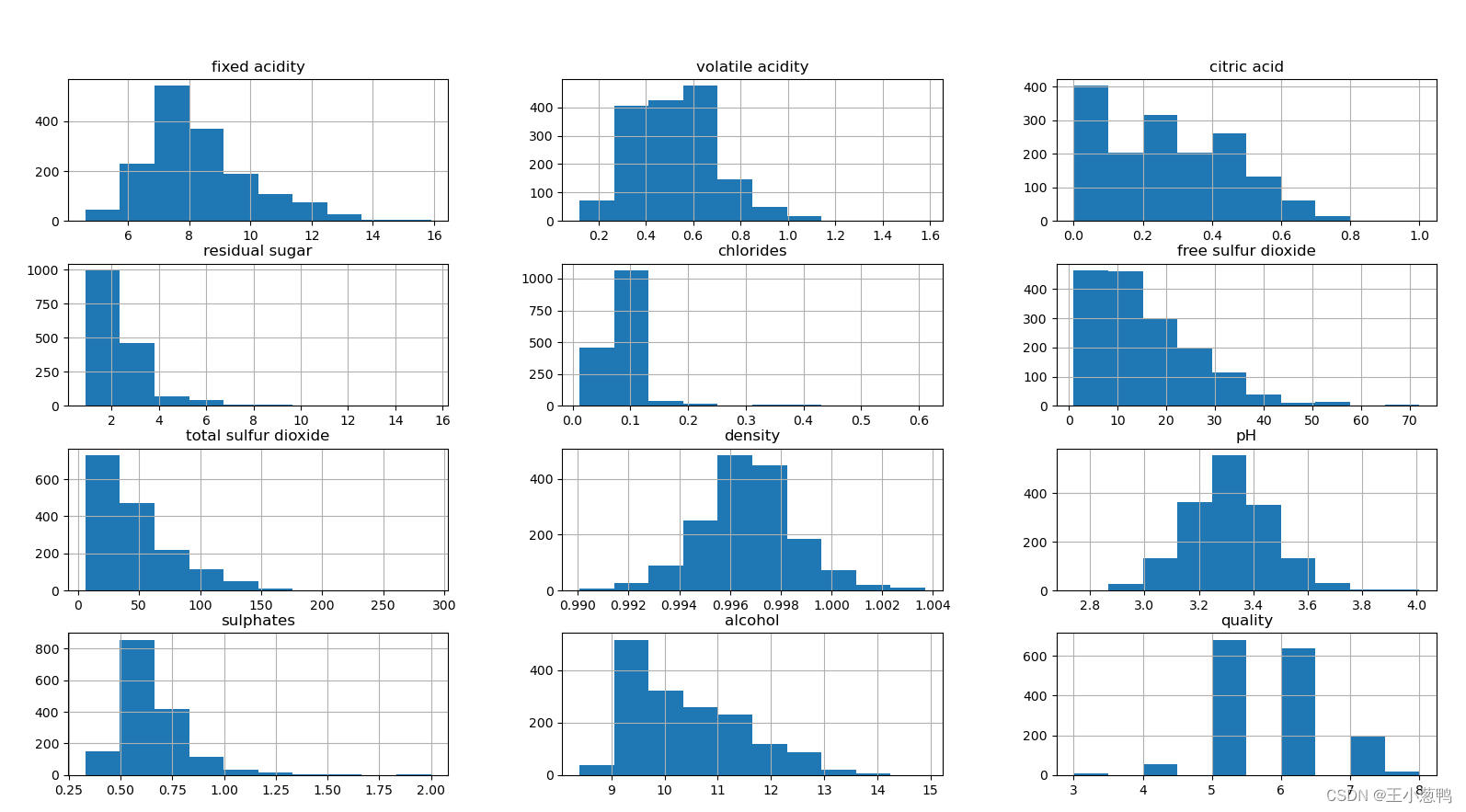
数据集划分，使用train_test_split划分，指定训练集占所有数据集比例0.7

x = data.drop(["quality"], axis=1)
y = data["quality"]
X_train, X_test, y_train, y_test = train_test_split(x, y, train_size=0.7, random_state=123)
print("数据集整体数量：{}".format(len(x)))
print("训练集集整体数量：{}".format(len(X_train)))
print("测试集整体数量：{}".format(len(X_test)))
1
2
3
4
5
6

数据集整体数量：1599
训练集集整体数量：1119
测试集整体数量：480
1
2
3

4 MinMaxScaler归一化

scaler = MinMaxScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
1
2
3
4

5 分别使用svm、knn、决策树、随机森林进行实验

clf = SVC()
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
svm_acc = accuracy_score(y_test, y_pred)
print("svm模型精度：{}".format(svm_acc))


clf = DecisionTreeClassifier()
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
dt_acc = accuracy_score(y_test, y_pred)
print("dt模型精度：{}".format(dt_acc))

clf = RandomForestClassifier()
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
rf_acc = accuracy_score(y_test, y_pred)
print("rf模型精度：{}".format(rf_acc))

clf = KNeighborsClassifier()
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
knn_acc = accuracy_score(y_test, y_pred)
print("knn模型精度：{}".format(knn_acc))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

svm模型精度：0.5833333333333334
dt模型精度：0.5645833333333333
rf模型精度：0.6541666666666667
knn模型精度：0.5666666666666667
1
2
3
4

通过结果可以看出随机森林效果最好.

6 使用PCA降维，然后使用随机森林进行分类

n_components = 8
pca = PCA(n_components= n_components)
pca.fit(X_train)
X_train = pca.transform(X_train)
X_test = pca.transform(X_test)
clf = RandomForestClassifier()
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
rf_acc = accuracy_score(y_test, y_pred)
print("pca维度为：{}, rf模型精度：{}".format(n_components, rf_acc))
1
2
3
4
5
6
7
8
9
10

pca维度为：8, rf模型精度：0.6791666666666667
1

通过结果，我们发现使用pca，精度提升了.

7 GridSearchCV调整rf的参数

我们只保留每次超参数调优时最好的结果，并且结合pca进行遍历。

param_grid = {"n_estimators":[10, 20, 50, 100]}
best_score = 0.0
for n_components in range(2, 10,2):
    pca = PCA(n_components=n_components)
    pca.fit(X_train)
    X_train_pca = pca.transform(X_train)
    clf = RandomForestClassifier()
    grid_search = GridSearchCV(clf, param_grid, cv=5)# 使用5折交叉验证
    grid_search.fit(X_train_pca,y_train)
    if grid_search.best_score_ > best_score:
        best_score = grid_search.best_score_
        best_pca = n_components
        best_rf_param = grid_search.best_params_
    print("pca维度为：{}, rf参数为：{}， rf模型精度：{}".format(n_components, grid_search.best_params_, grid_search.best_score_))
1
2
3
4
5
6
7
8
9
10
11
12
13
14

pca维度为：2, rf参数为：{'n_estimators': 100}， rf模型精度：0.6050128122998079
pca维度为：4, rf参数为：{'n_estimators': 100}， rf模型精度：0.6416359705317104
pca维度为：6, rf参数为：{'n_estimators': 50}， rf模型精度：0.6469971172325433
pca维度为：8, rf参数为：{'n_estimators': 20}， rf模型精度：0.670199391415759
1
2
3
4