Java：二叉树（1）

  从现在开始，我们进入二叉树的学习，二叉树是数据结构的重点部分，在了解这个结构之前，我们先来了解一下什么是树型结构吧！

一、树型结构

1、树型结构简介

  树是一种非线性的数据结构，它是由n（n>=0)个有限结点组成的具有层次关系的集合。把它叫成树，是因为它看起来很像棵倒挂的树，也就是说，它是根朝上，叶朝下的。

  树具有以下几个特点：

1、有一个特殊的结点，称为根结点，它没有前驱结点。

2、除了根结点以外，其余结点被分为M（M>0)个互不相交的集合T1 、T2 、T3 ……Tm,其中每一个集合又是一棵类似的子树。

---

---

2、树型结构的判断

如图：

1、A便是根结点，其余的B、C、D、E等都可以称为子树！

2、以此图，我们再引入两个概念：

父结点：有衍生出子类的结点称为父结点。比如A衍生出B、C、D，因此A是B、C、D结点的父结点！

子结点：父结点衍生出来的结点称为子结点。比如B、C、D都是A的子结点！

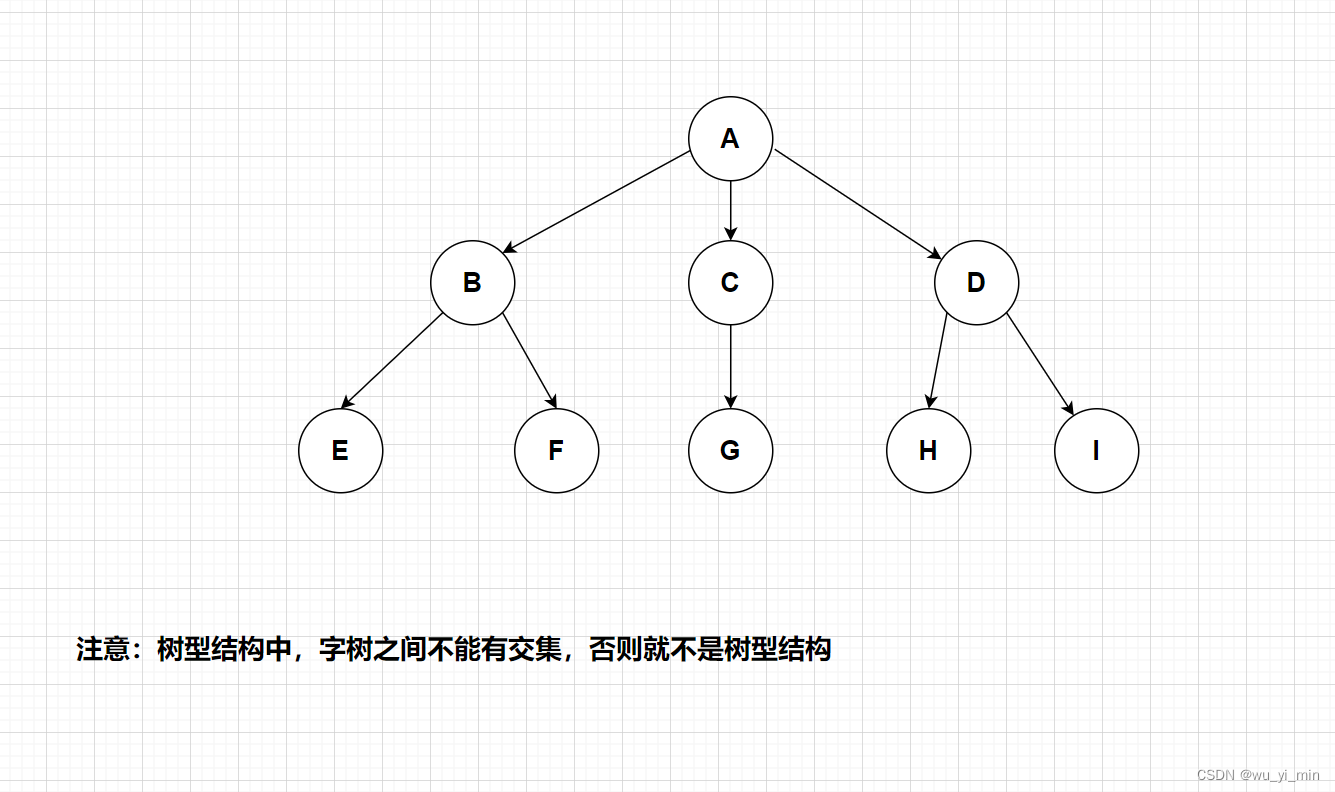
 注意：子树之间不能有交集。

子树之间有没有交集判断时有一个依据：  除了根结点以外，每个结点有且只有一个父结点！

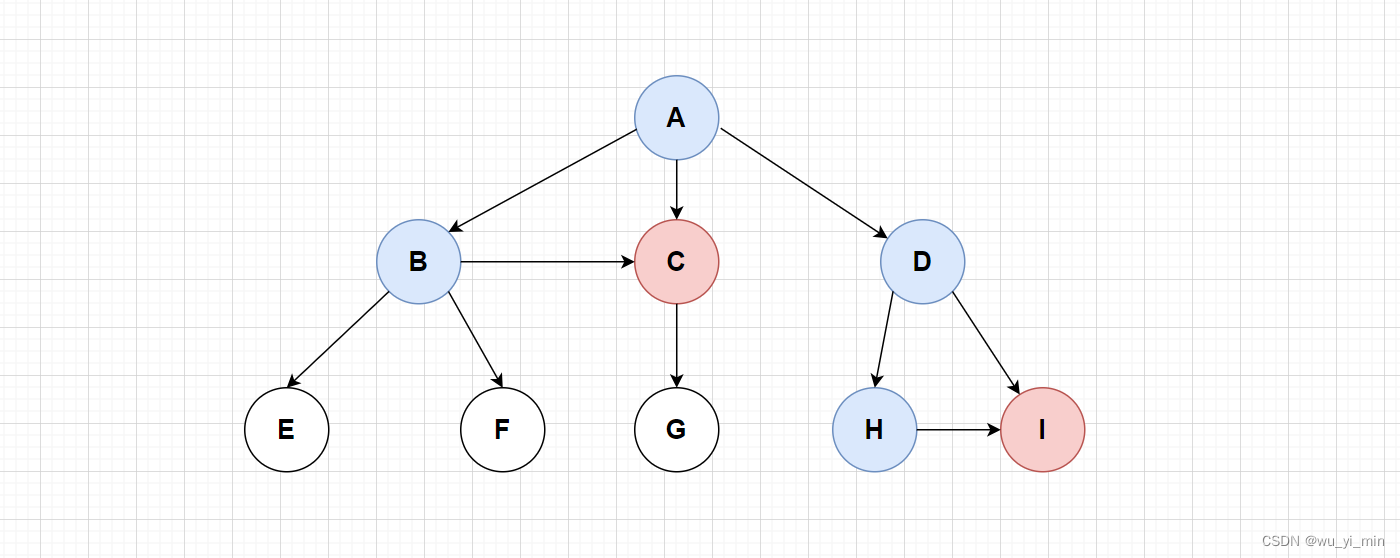
分析此图：

1、C结点有 A 和 B两个父结点

2、I 结点有  D 和 H 两个父结点

因此，这个结构不是树型结构

---

---

3、树型结构的一些重要概念

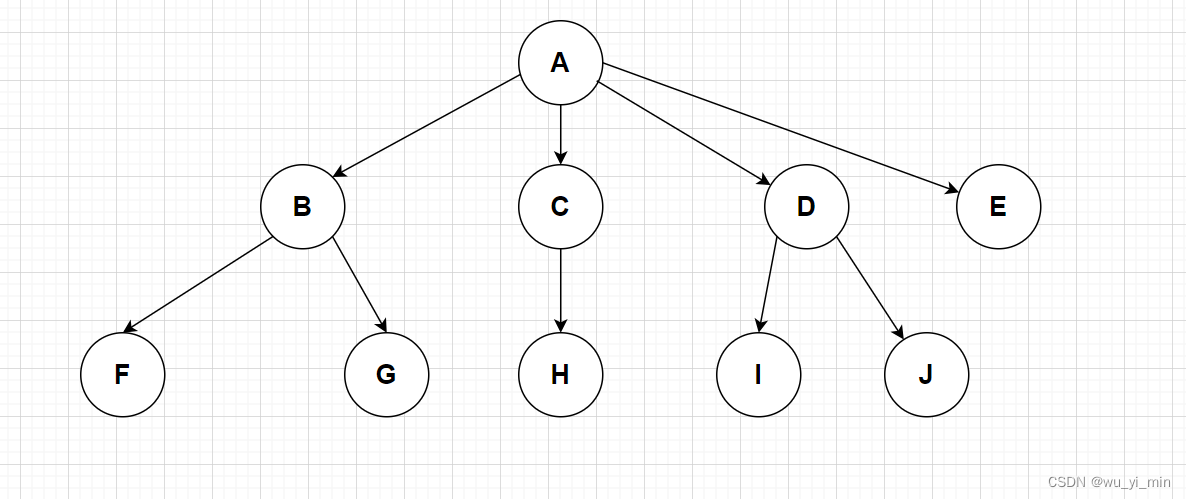
1、结点的度：一个结点含有子树的个数称为该结点的度 ，如上图：A的度为4，D的度为2

2、树的度：一棵树中，所有结点度的最大值称为该树的度，如上图：该树的度为4

3、叶结点或终端结点：度为0的结点称为叶结点，如上图，E、F、G、H、J都称为叶结点

4、结点的层次：从根开始定义起，根为第一层，根的子结点为第二层，以此类推。

5、树的高度：即树中结点的最大层次，如图，该树的高度是3。

6、兄弟结点：拥有同一个父结点的称为兄弟结点，比如B、C、D、E互为兄弟结点。

7、堂兄弟结点：父结点在同一层次的称为堂兄弟结点，比如G和H互为堂兄弟结点。

---

---

二、二叉树 【概念】

1、什么是二叉树

二叉树是结点的一个有限集合，该集合

1、或者为空

2、或是是由一个根结点加上两棵分别称为左子树和右子树的二叉树组成！

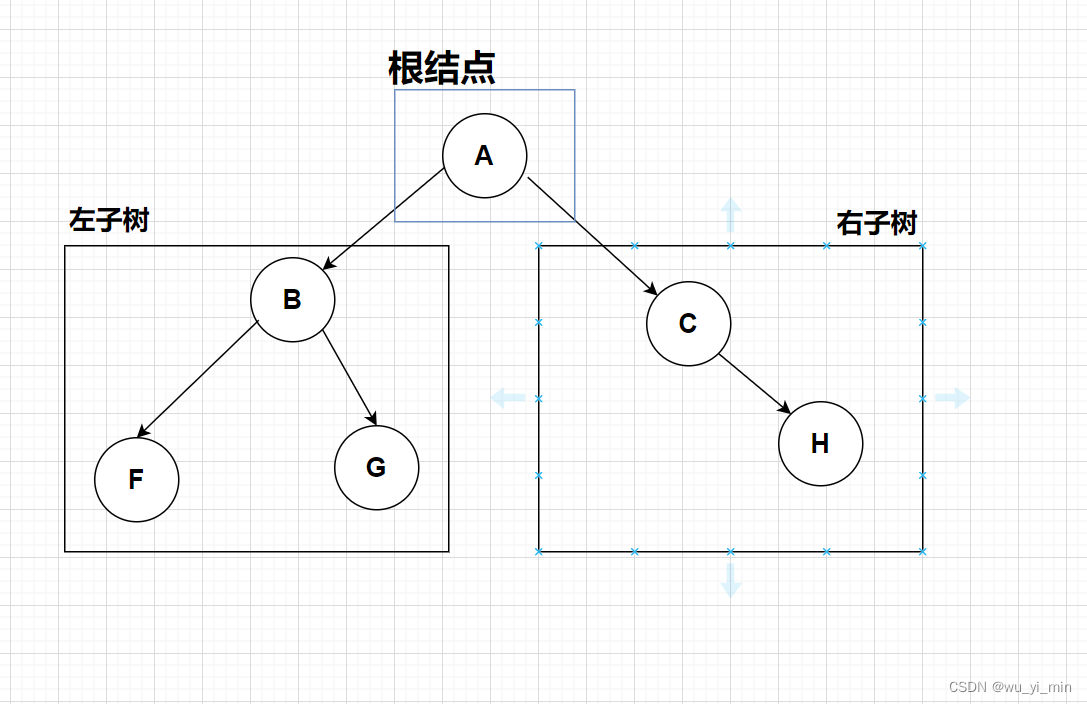
那为什么称为二叉树？

答：此树不存在度大于2的结点 。从上图可以看到，每个结点的度都不会超过2，因此它称为二叉树！

---

---

2、两种特殊的二叉树

1、满二叉树：

一颗二叉树，如果每层的结点数都达到最大值，则这棵树称为满二叉树，换言之，如果一棵二叉树的层数为K，且结点数是2^k -1，则它就是满二叉树！

如图：

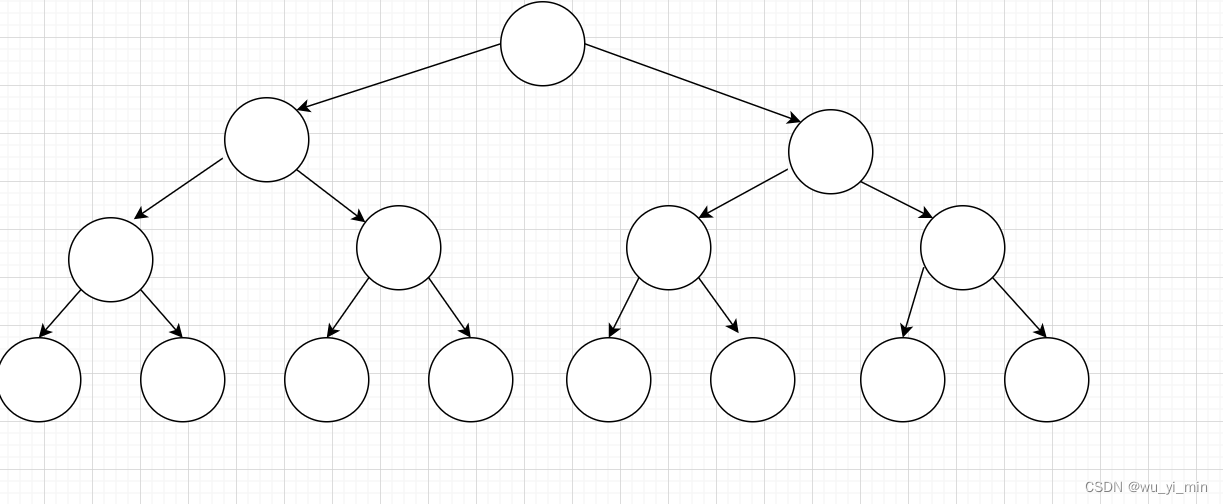
2、完全二叉树：

对于层数为k的，结点数为n的二叉树，当且仅当其每一个结点都与层数为k的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树！

通俗点说，就是将结点从上到下，从左到右依次存放！

比如此图，它就是一个完全二叉树，它的每个结点都是按照右从上到下，从左到右依次存放！

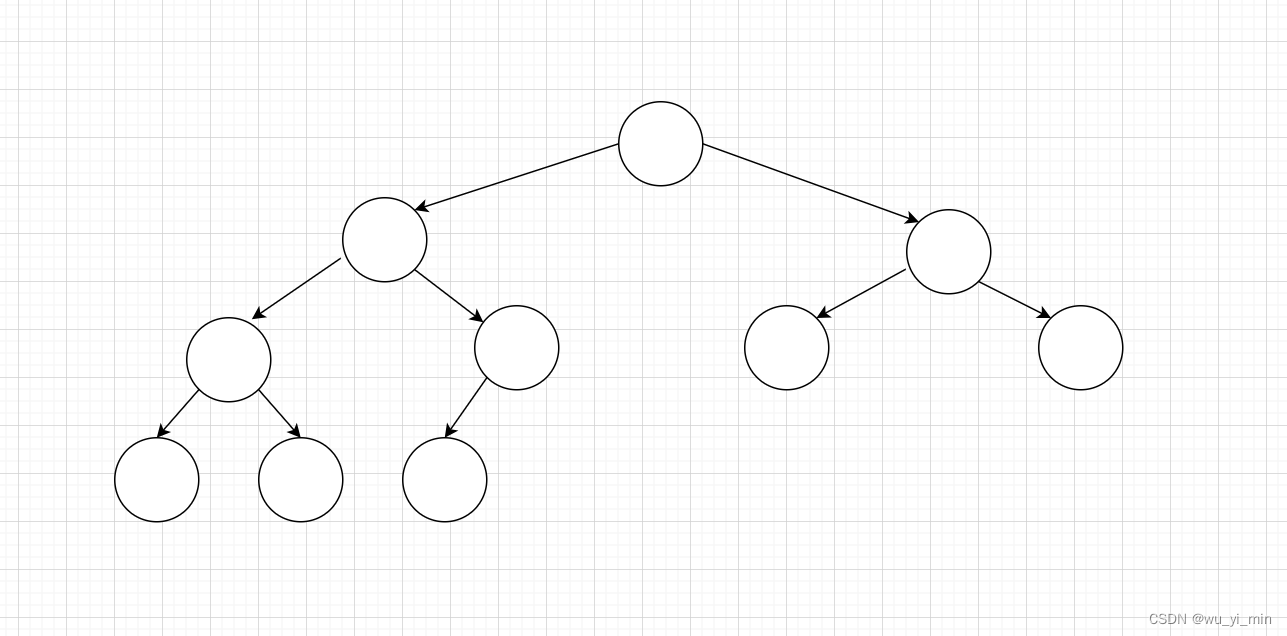
举一个不是完全二叉树的反例：

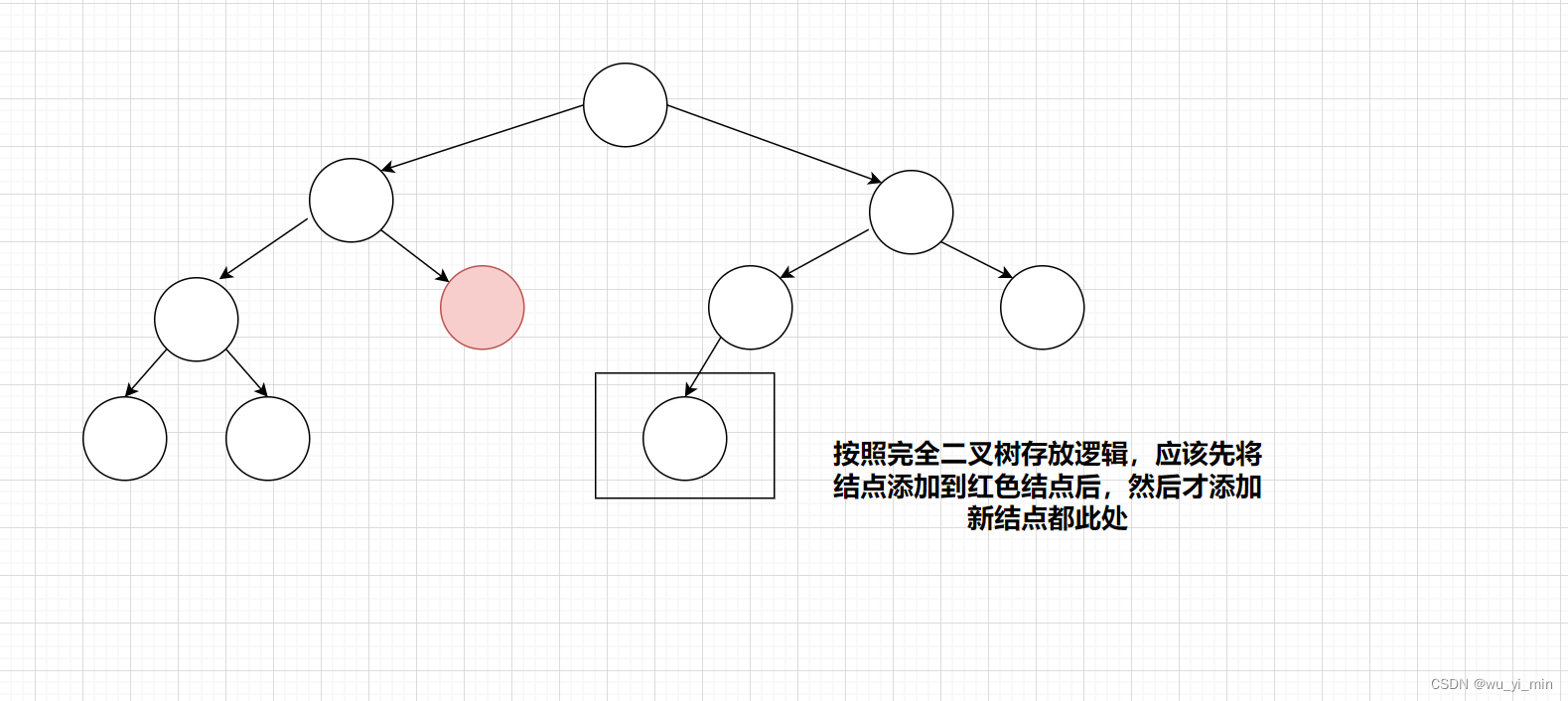
那么，我们将其修改成完全二叉树，看看需要怎么操作？

只需要将给红色结点添加两个子结点，此时，这个又是一个完全二叉树！

---

---

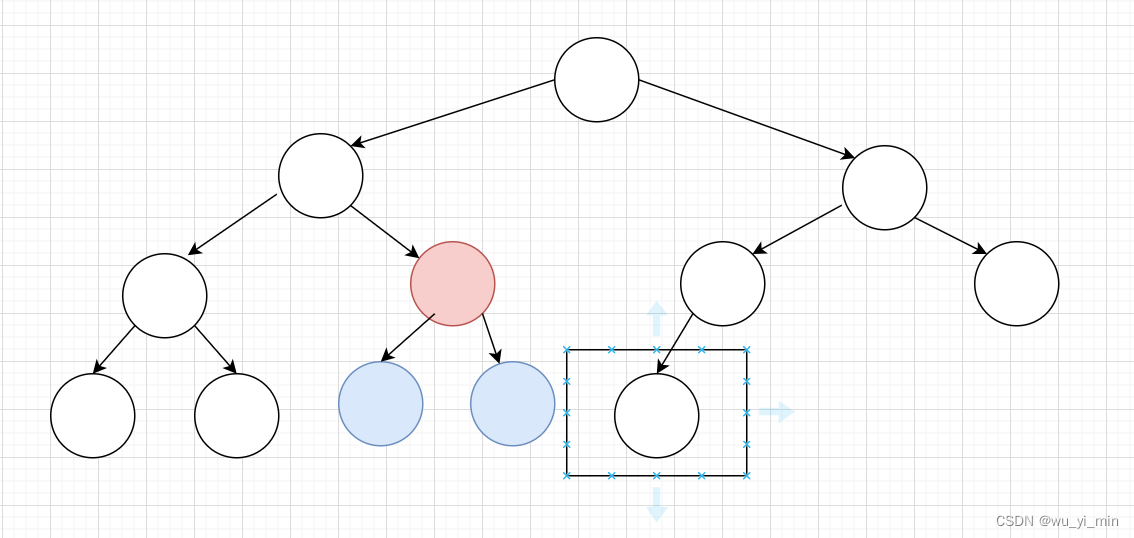
3、二叉树的性质 

1、对于任何一棵二叉树，如果叶结点个数为n0，度为2的非叶结点个数为n2，则有n0=n2+1 

如果有兴趣的伙伴，我们可以来推导一下这个公式。

这个推导基于我们知道一个事实：一棵N个结点的树有N-1条边

推导过程：

假设二叉树度为0的结点个数为n0、度为1的结点个数为n1、度为2的结点个数为n2。

那么我们可以知道，度为0的结点可以产生0条边，度为1的结点可以产生1条边，度为2的结点可以产生2条边！

就有：N-1=n1+n2+n2

           N=n0+n1+n2

将2式代入1式：n0+n1+n2-1=n1+n2+n2   ------>>   n0=n2+1

---

2、具有n个结点的完全二叉树的高度k为log2（n+1）上取整

如图，该完全二叉树有10个结点，log2（11）的结果是在3和4之间的，那么就向上取整，因此其高度是4！

---

3、对应具有n个结点的完全二叉树，如果按照从上至下，从左至右的顺序对所有结点从0开始编号，则对于序号为i的结点有：

》若i>0，父结点序号为：（i-1）/2  ；若i=0；无父结点：

如图：

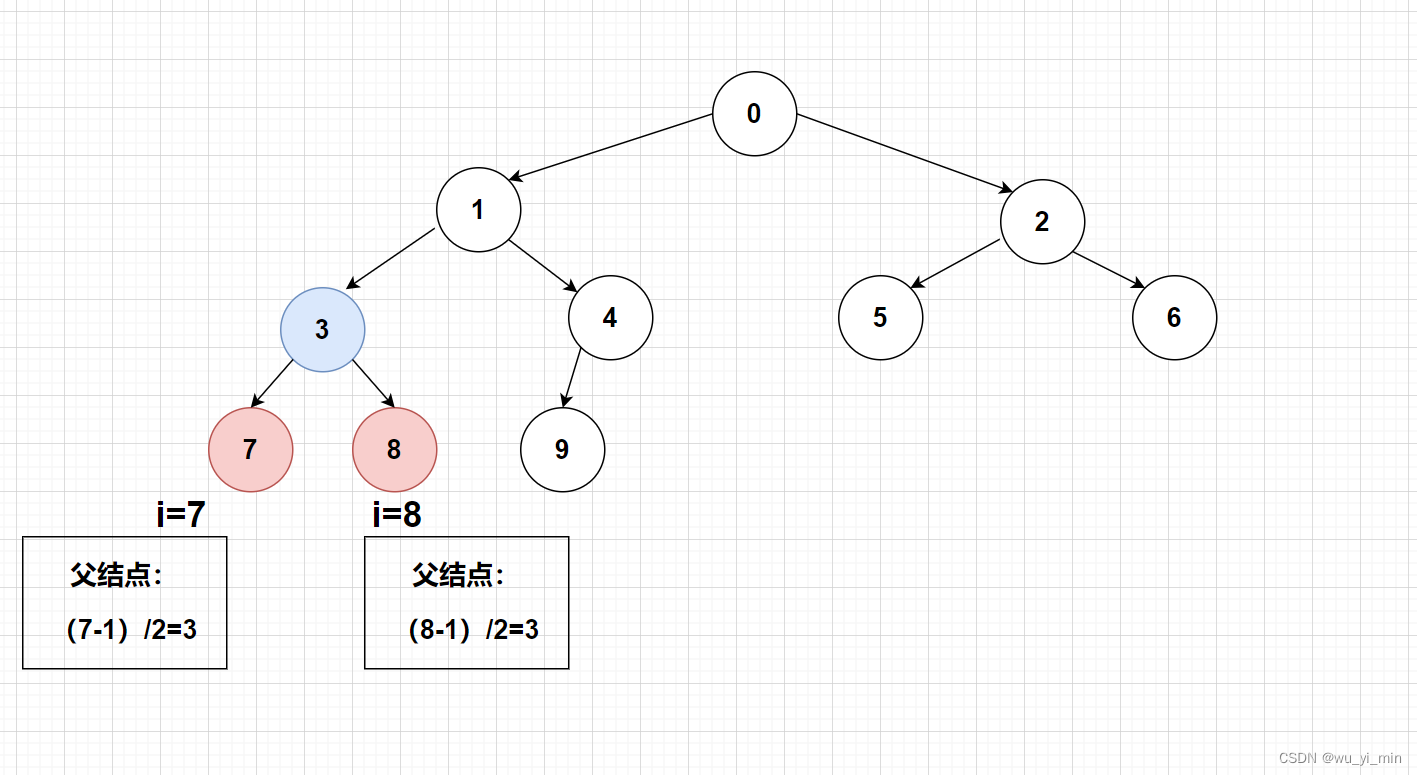
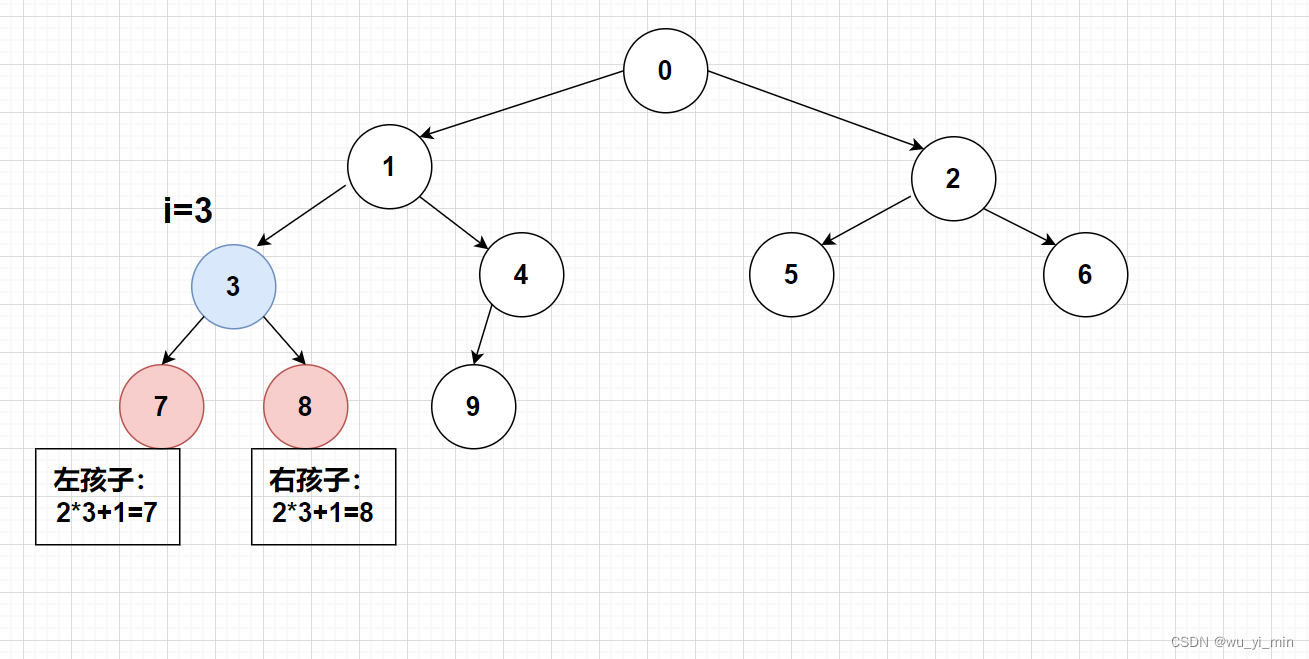
》若2i+1<n，则下标为i的结点的左孩子序列为2i+1；否则就是无左孩子

》若2i+2<n，则下标为i的结点的右孩子序列为2i+2；否则就是无右孩子 

如图：

---

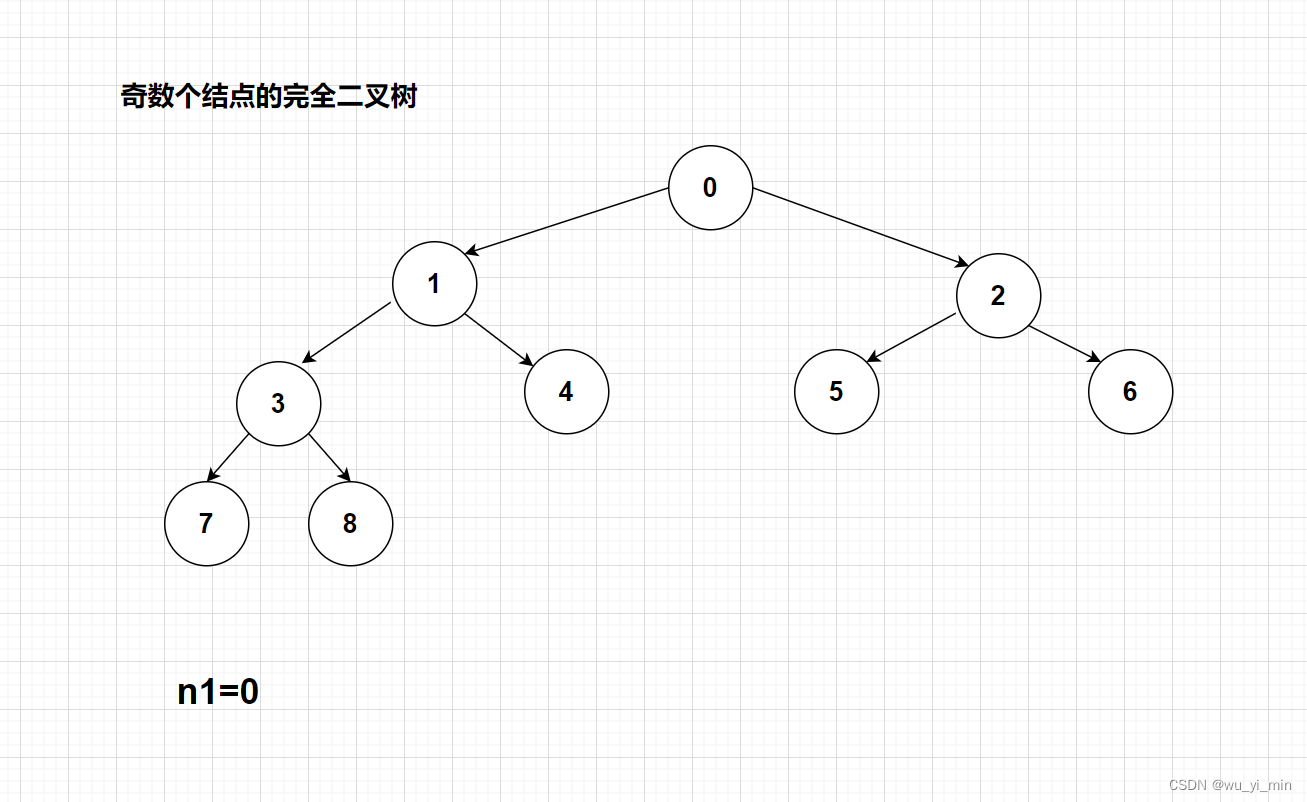
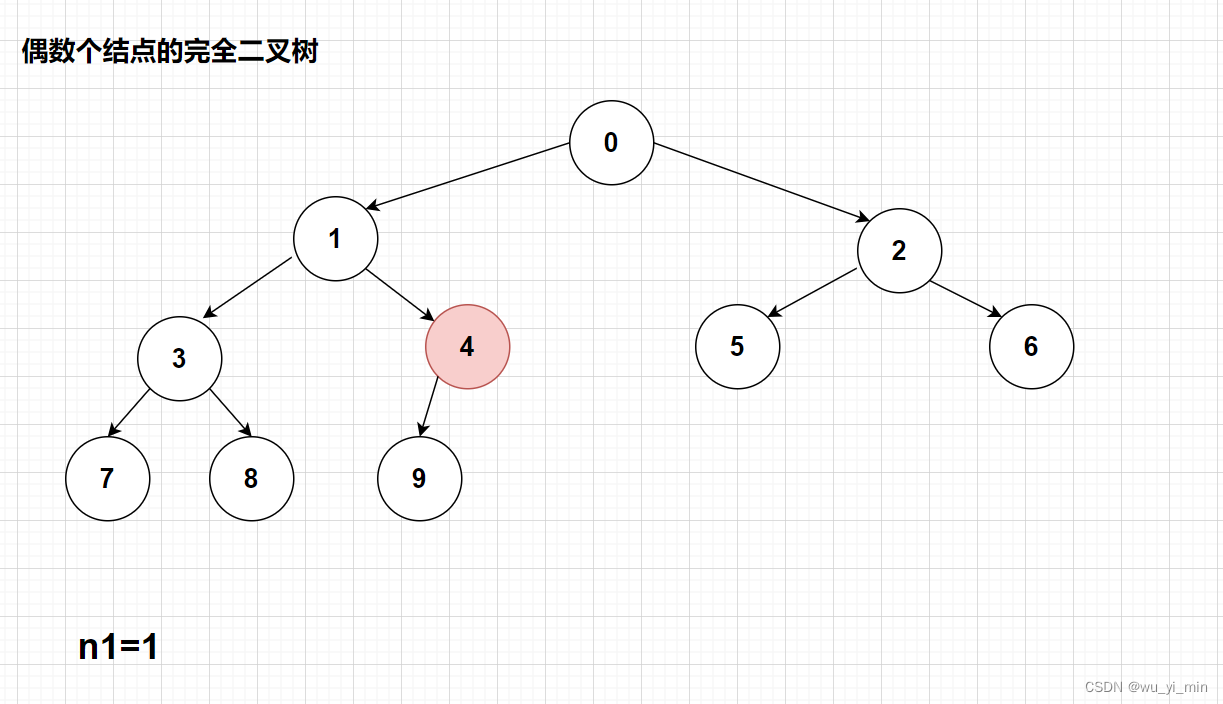
4、有奇数个结点的完全二叉树， 度为1的结点个数为0；有偶数个结点的完全二叉树，度为1的结点个数为1。

---

---

 三、二叉树的存储

1、二叉树的节点

二叉树的存储结构分为:顺序存储和类似于链表的链式存储

现在我们不介绍顺序存储，我们先来学习链式存储！

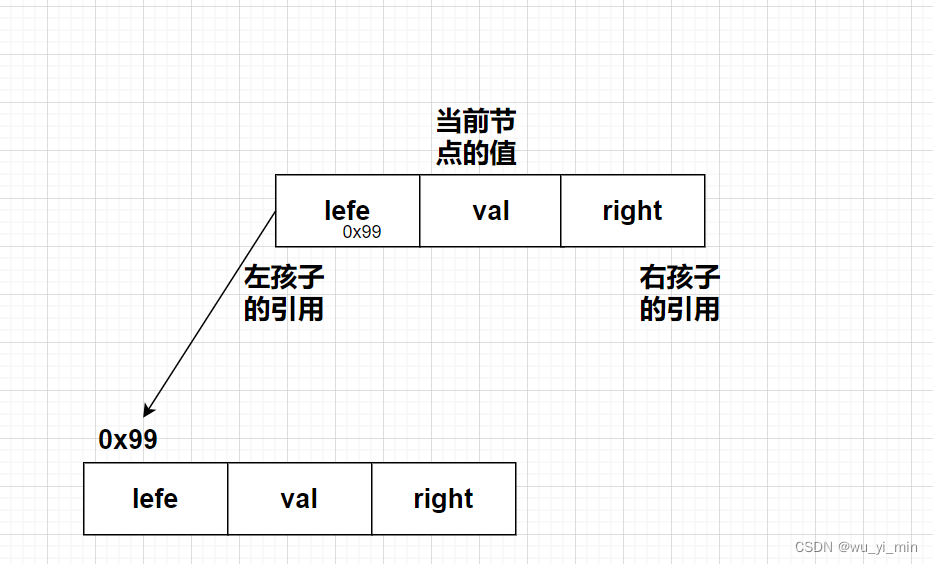
二叉树的链式存储是由一个一个的节点连接起来的，每个节点包含三个域。

class Node{
int val;      //数据域
Node left;    //左孩子的引用
Node right;   //右孩子的引用
}

---

---

 2、二叉树的遍历

  前面我们学习链表和顺序表的时候，其实本质上都是在遍历链表和顺序表，以此完成增删查改操作，由于二叉树是非线性结构，因此其遍历的方式比较不同，所有在实现二叉树之前，让我们先来了解一下二叉树的遍历方法！ 

二叉树有以下四种遍历方法：

》前序遍历：  根、左、右（先遍历根节点，然后再遍历左子树，最后遍历右子树）

》中序遍历：  左、 根 、右（先遍历左子树，然后遍历根节点，最后遍历右子树）

》后序遍历：  左 、右 、根（先遍历左子树，然后遍历右子树，最后遍历根节点）

》层序遍历： 从上到下，从左到右  依次遍历

让我们以打印二叉树结点数据为例子，看看不同的遍历序列有什么不同：

前序遍历：根  左  右（先遍历根节点，然后再遍历左子树，最后遍历右子树）

注意：图中的数字代表二叉树遍历的前后顺序！蓝色箭头为即遍历路径 ！无论使用何种遍历方式，遍历路径都是不变的！

前序遍历要求：无需遍历树的左右子树便可以打印该节点的内容；

听不懂也没有关系，只要我们结合下面三种遍历方式的不同便可以深刻的理解了！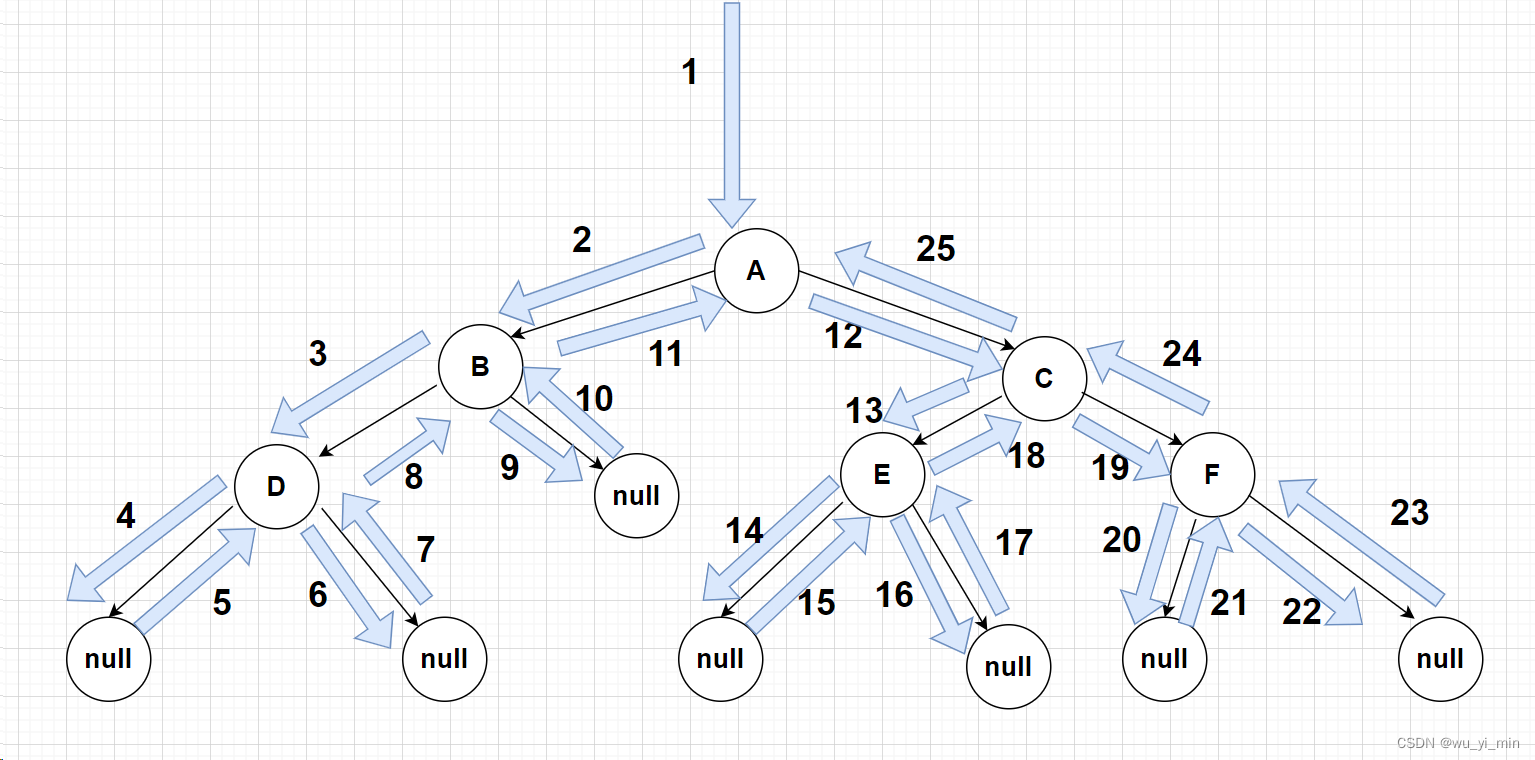

进入A（打印A），把A作为根节点，再遍历节点A的左子树， 

进入B（打印B），把B看作新的根节点，再遍历B的左子树；

进入D（打印D），把D看作新的根节点，再遍历D的左子树；

发现D的左子树为null，回到D，再遍历D的右子树；

发现D的右子树为null，回到D；

（注意：此时完成了第一颗树D的遍历）

回到B,再遍历B的右子树；

发现B的右子树为null，回到B；

（注意：此时完成了第二棵树B的遍历）

回到A，再遍历A的右子树C；

进入C（打印C），把C看作新的根节点，再遍历C的左子树；

进入E（打印E），把E看作新的根节点，再遍历E的左子树，

发现E的左子树为null，回到E，再遍历E的右子树；

发现E的右子树为null，回到E；

（注意：此时完成了第三棵树E的遍历）

回到C，再遍历C的右子树F；

进入F（打印F），把F看作新的根节点，再遍历F的左子树；

发现F的左子树为null，回到F；再遍历F的右子树；

发现F的右子树为null，回到F；

（注意：此时完成了第四棵树F的遍历）

回到C；

（注意：此时完成了第五颗树C的遍历）

回到A；

（注意：此时全部的树都已经遍历完成）

因此，前序遍历打印的结果为：ABDCEF

---

中序遍历：  左、 根 、右（先遍历左子树，然后遍历根节点，最后遍历右子树）

中序遍历的时候，二叉树的遍历路径也是一样的，但是中序遍历要求：只有在完成每一棵树的左子树的遍历后，才可以打印该节点的内容；

比如，第一次进入A的时候，不能直接打印，要等A树的左子树遍历完成，再次回到A时才可以打印A。

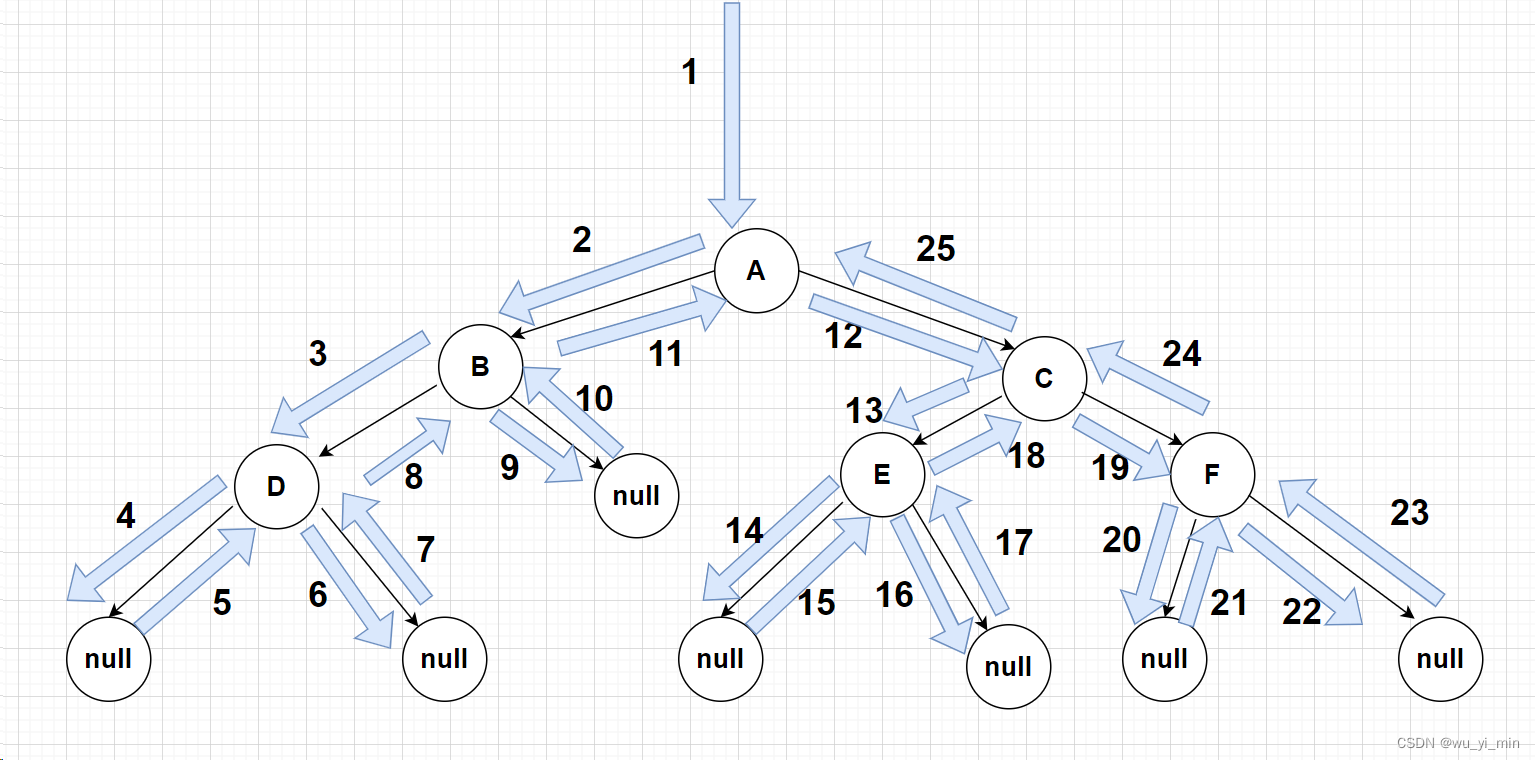
进入A，把A作为根节点，再遍历A的左子树；

进入B，把B作为新的根节点，再遍历B的左子树；

进入D，把D作为新的根节点，再遍历D的左子树；

发现D的左子树为null，回到D，再遍历D的右子树；（此时D树的左子树遍历完成，可以打印D）

发现D的右子树为null，回到D；

（注意：此时完成第一棵树D的遍历）

回到B，然后再遍历B的右子树；（此时B树的左子树遍历完成，可以打印B）

发现B的右子树为null，回到B；

（注意：此时完成第二棵树B的遍历）

回到A，然后再遍历A的右子树C；（此时A树的左子树遍历完成，可以打印A）

进入C，把C看作新的根节点，再遍历C的左子树；

进入E，把E看作新的根节点，再遍历E的左子树；

发现E的左子树为null，回到E，再遍历E的右子树；（此时E树的左子树遍历完成，可以打印E）

发现E的右子树为null，回到E；

（注意：此时完成第三棵树E的遍历）

回到C，再遍历C的右子树F；（此时C树的左子树遍历完成，可以打印C）

进入F，把F看作新的根节点，再遍历F的左子树；

发现F的左子树为null，回到F，再遍历F的右子树；（此时F树的左子树遍历完成，可以打印F）

发现F的右子树为null，回到F；

（注意：此时完成第四棵树F的遍历）

回到C；

（注意：此时完成第五课树C的遍历）

回到A；

（注意：此时完成全部树的遍历）

因此，中序遍历打印的结果为：DBAECF

---

后序遍历：  左 、右 、根（先遍历左子树，然后遍历右子树，最后遍历根节点）

 后序遍历时，要求完成每一棵树的左右子树的遍历，才可以打印该节点的内容；

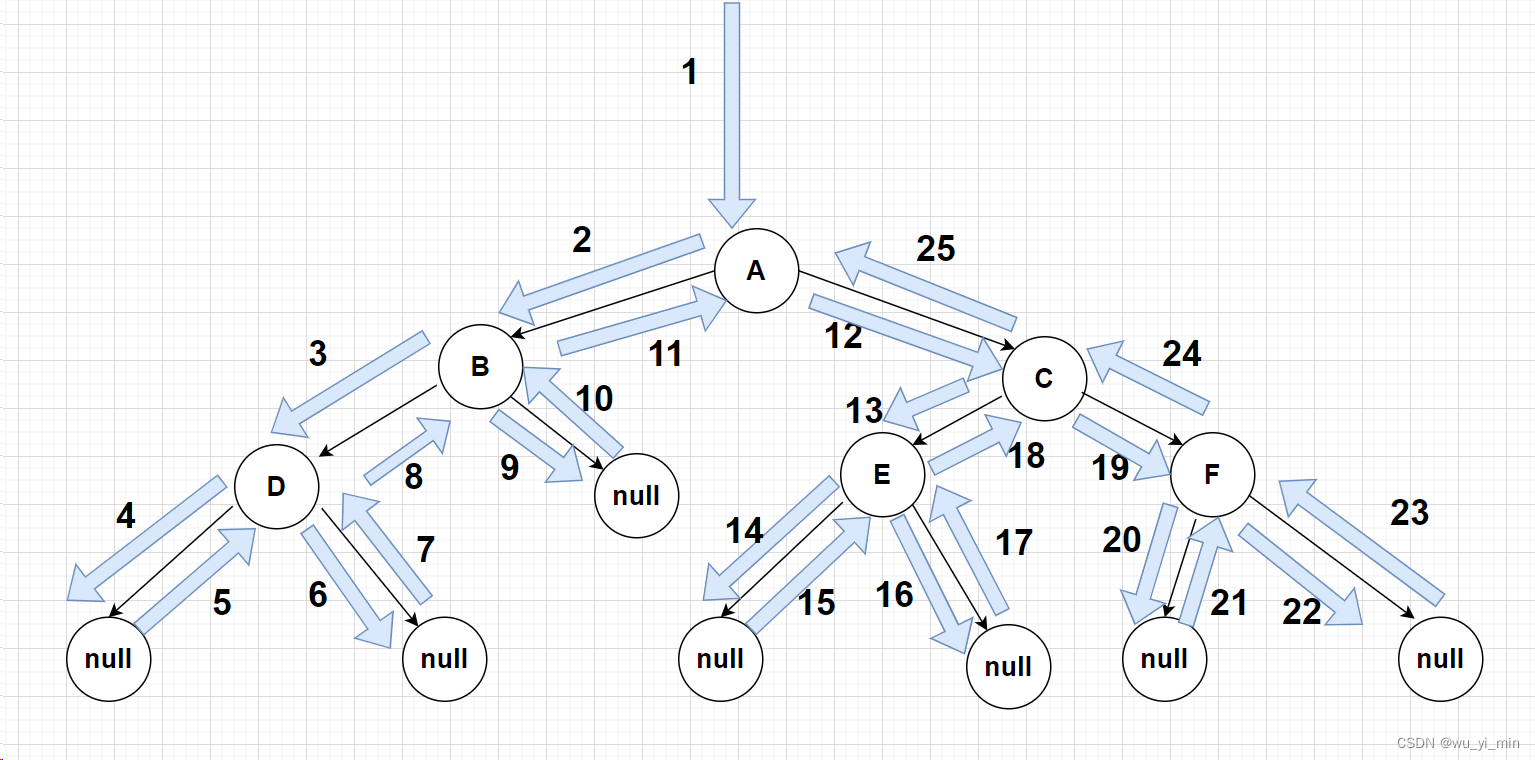
进入A，把A作为根节点，再遍历A的左子树；

进入B，把B作为新的根节点，再遍历B的左子树； 

进入D，把D作为新的根节点，再遍历D的左子树；

发现D的左子树为null，回到D，再遍历D的右子树；

发现D的右子树为null，回到D；（此时D树的左右子树遍历完成，可以打印D）

（注意，此时完成第一颗树D的遍历）

回到B，再遍历B的右子树；

发现B的右子树为null，回到B；（此时B树的左右子树遍历完成，可以打印B）

（注意，此时完成第二棵树B的遍历）

回到A，再遍历A的右子树C；

进入C，把C作为新的根节点，再遍历C的左子树；

进入E，把E作为新的根节点，再遍历E的左子树；

发现E的左子树为null，回到E，再遍历E的右子树；

发现E的右子树为null，回到E；（此时E树的左右子树遍历完成，可以打印E）

（注意：此时完成第三棵树E的遍历）

回到C，再遍历C的右子树；

进入F，把F作为新的根节点，再遍历F的左子树；

发现F的左子树为null，回到F，再遍历F的右子树；

发现F的右子树为null，回到F；（此时F树的左右子树遍历完成，可以打印F）

（注意：此时完成第四棵树F的遍历）

回到C；（此时C树的左右子树遍历完成，可以打印C）

（注意：此时完成第五颗树C的遍历）

回到A；（此时A树的左右子树的遍历完成，可以打印A）

（注意：此时完成全部树的遍历）

因此，后序遍历打印的结果为：DBEFCA

层序遍历的情况暂且不作讲解，大家有兴趣可以自行了解！

---

---

四、二叉树的实现

现在我们万事俱备，是时候来了解一下二叉树的实现了！

类文件，首先，我们先创建一个TestBinaryTree类，用来实现我们的二叉树；

这个Test类，用来测试我们的二叉树！

1、节点类：

通过前面的学习，我们知道，二叉树的每一个节点包含三个域：left、val、right；

因此，我们需要在TestBinaryTree类内部定义一个内部的节点类！

 

内部类的实现：

注意，这个Node类是定义在TestBinaryTree类的内部的！

---

---

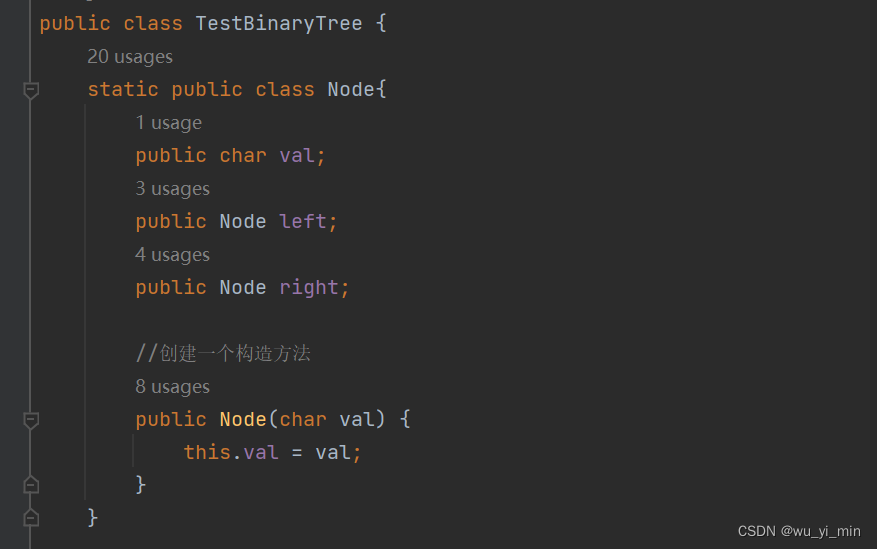
2、创建一个简易的二叉树： 

在实现遍历方法之前，我们需要创建一个二叉树！这里我们不妨在TestBinaryTree类内部实现一个方法，创建一个如图的二叉树！

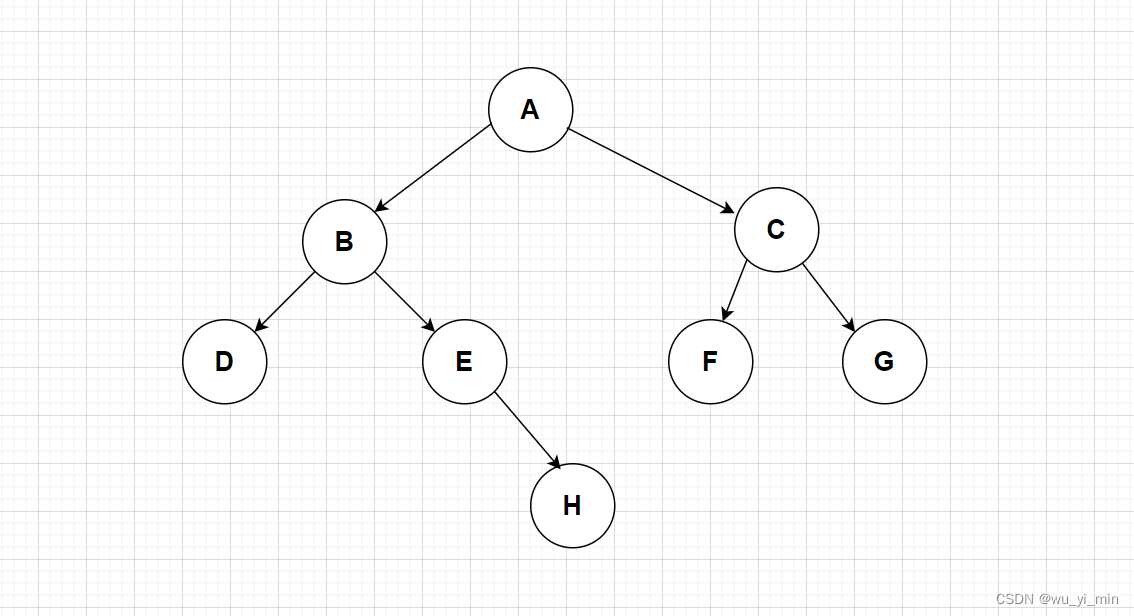
 //实现一个方法：该方法可以简易创建一个二叉树
    public Node createTree(){
        //实例化几个对象
        Node A=new Node('A');
        Node B=new Node('B');
        Node C=new Node('C');
        Node D=new Node('D');
        Node E=new Node('E');
        Node F=new Node('F');
        Node G=new Node('G');
        Node H=new Node('H');
 
        //连接这几个对象
        A.left=B;
        A.right=C;
        B.left=D;
        B.right=E;
        C.left=F;
        C.right=G;
        E.right=H;
 
        return A;
    }

---

---

3、前序遍历方法：  

 
    //实现前序遍历:根、左、右
    public void preOrder(Node root){
        //如果root==null，返回
        if(root==null){
            return;
        }
        //先打印根节点内容
        System.out.print(root.val+" ");
        //再遍历左子树
        preOrder(root.left);
        //最后遍历右子树
        preOrder(root.right);
    }

这个方法是通过递归实现，因此我们还是举一个例子来让大家充分理解它的递归过程！

以如下图的二叉树为例子！

 

---

---

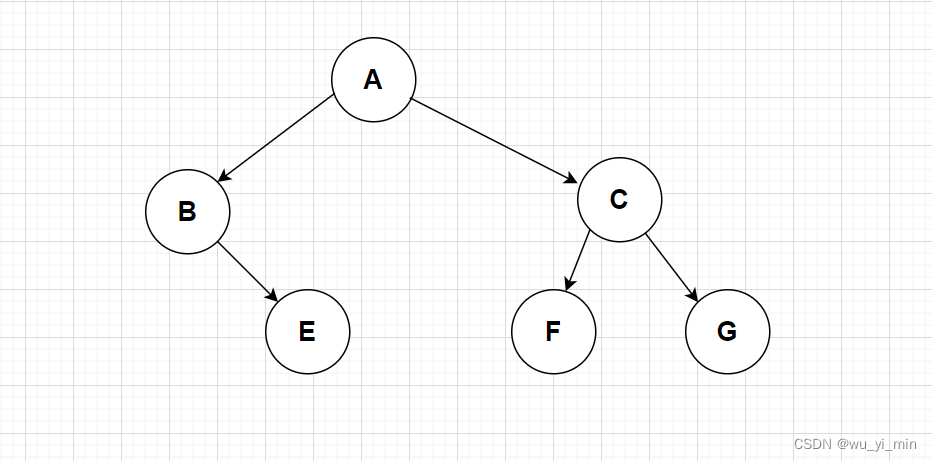
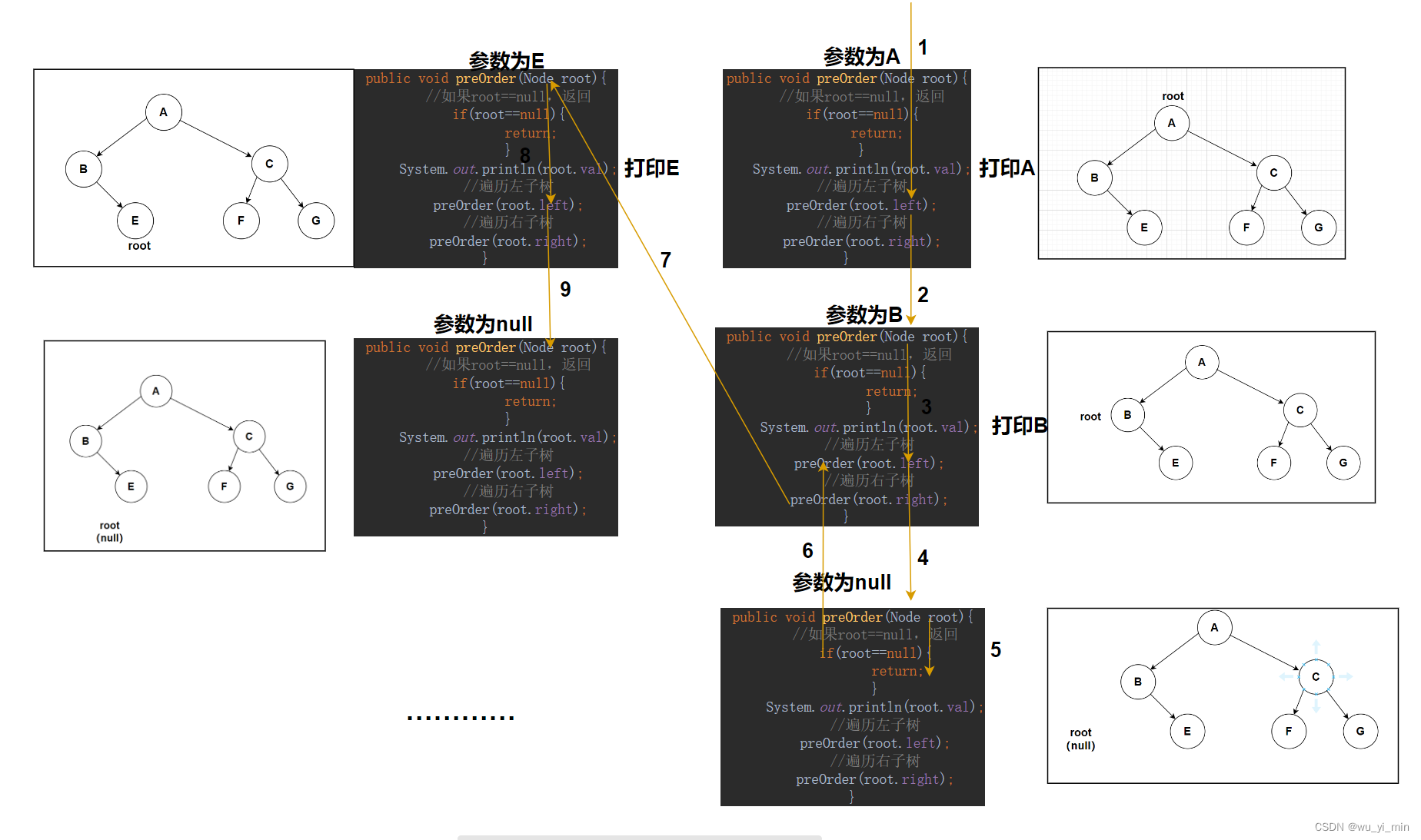
4、中序遍历方法：

//实现中序遍历：左、根、右
    public void inOrder(Node root){
        if(root==null){
            return;
        }
        //先遍历左子树
        inOrder(root.left);
        //再打印根节点内容
        System.out.print(root.val+" ");
        //最后遍历右子树
        inOrder(root.right);
    }

---

---

5、后序遍历方法：

 //实现后序遍历：左、右、根
    public void postOrder(Node root){
        if(root==null){
            return;
        }
        //先遍历左子树
        postOrder(root.left);
        //再遍历右子树
        postOrder(root.right);
        //最后打印根节点内容
        System.out.print(root.val+" ");
    }

---

---

6、遍历方法的运行结果

---

---

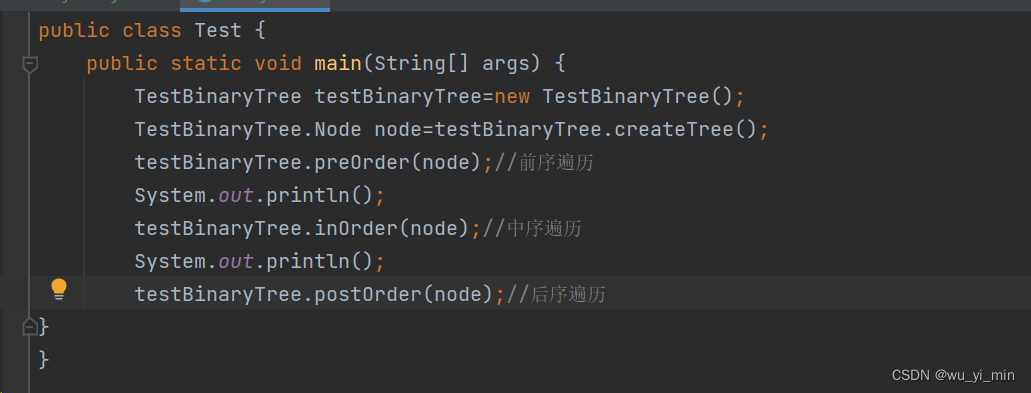
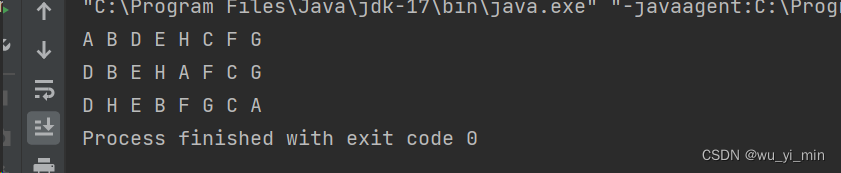
7、计算二叉树节点个数的方法：

首先，我们需要知道

树的节点个数=左子树的节点个数+右子树的节点个数+1 

这个1就是代表这棵树的根节点，在实际计算的过程当中，我们又可以将每一个节点看作一颗树，因此，这个方法我们使用递归实现！

//计算二叉树的节点个数
    public int size(Node root){
        if(root==null){
            return 0;
        }
        int ret=size(root.left)+size(root.right)+1;
        return ret;
    }

---

---

8、计算叶子节点的个数的方法：

这里我们需要弄清楚一个点，什么是叶子节点，叶子节点就是没有左右子树的节点！

计算的主体逻辑：叶子节点的个数=左子树叶子节点的个数+右子树叶子节点的个数

 //计算二叉树的叶子节点的个数
    public int getLeafNodeCount(Node root){
        if(root==null){
            return 0;
        }
        //叶子节点
        if(root.left==null&&root.right==null){
            return 1;
        }
        int ret=getLeafNodeCount(root.left)+getLeafNodeCount(root.right);
        return ret;
    }

---

---

9、计算第K层有几个节点的方法：

  //计算第K层有多少个节点
    public int getKLevelNodeCount(Node root,int k){
        if(k==0){
            return 0;
        }
        if(k==1){
            return 1;
        }
        return getKLevelNodeCount(root.left,k-1)+
                getKLevelNodeCount(root.right,k-1);
    }

---

---

10、计算整棵树的高度的方法：

整棵树的高度=左子树高度和右子树高度中的最大值

 
    //计算二叉树的高度
    public int getHeight(Node root){
        if(root==null){
            return 0;
        }
 
        int leftHeight=getHeight(root.left);
        int rightHeight=getHeight(root.right);
 
        return leftHeight>rightHeight?leftHeight+1:rightHeight+1;
    }

---

---

11、查找某个值的方法：

 //找到值为val的节点
    public Node find(Node root,char val){
        if(root==null){
            return null;
        }
        if(root.val==val){
            return root;
        }
        Node nodeLeft=find(root.left,val);
        if(nodeLeft!=null){
            return nodeLeft;
        }
        Node nodeRight= find(root.right,val);
        if(nodeRight!=null){
            return nodeRight;
        }
        //找不到，返回null
        return null;
    }