人工智能与数学前沿综述：如何借助 AI 发现数学规律？

导语

为了探索数学与人工智能深度融合的可能性，集智俱乐部联合同济大学特聘研究员陈小杨、清华大学交叉信息学院助理教授袁洋、南洋理工大学副教授夏克林三位老师，共同发起“人工智能与数学”读书会，希望从 AI　for　Math，Math　for　AI 两个方面深入探讨人工智能与数学的密切联系。

在人工智能与数学读书会第一期，陈小杨老师探讨了符号回归、强化学习构造反例、AI辅助发现数学规律，以及大语言模型在数学研究中的应用，并分享了一些最新研究成果。在以 ChatGPT 为代表的大语言模型集中爆发的当下，如何利用语言大模型，构建一个人机交互的数学研究平台？陈老师介绍了最新发布的 DeepMath 数学大模型。本文是此次读书会的文字整理。

读书会回放视频已上线，欢迎感兴趣的朋友报名读书会，观看回放视频

https://pattern.swarma.org/study_group_issue/518

研究领域：AI for Math，符号回归，强化学习，大语言模型

来源：集智俱乐部

分享：陈小杨 

整理：黄雨

编辑：梁金 

目录

1. 人工智能和神经网络的背景知识

2. 计算机辅助数学研究

    2.1 符号回归寻找数学表达式

    2.2 强化学习构造猜想反例

    2.3 AI 辅助发现数学规律

3. 大语言模型在数学研究中的应用

4. 人机交互的数学研究平台

5. 展望：如何借助 AI 发现新的数学概念？

1. 人工智能和神经网络的背景知识

回顾人工智能和神经网络的发展历史，人工智能（Artificial Intelligence）是指让机器具有人类的智能，其诞生的标志性事件是1956 年的达特茅斯（Dartmouth）会议，在这次会议 上，“人工智能”被提出并作为本研究领域的名称。

图：人工智能的发展历史与标志性事件

神经网络在数学上可以被解读为一种特殊的函数。这种函数通过自变量x的线性组合，然后通过激活函数φ进行处理，再进行线性组合后得到输出。φ函数可以有多层，构成复合函数。

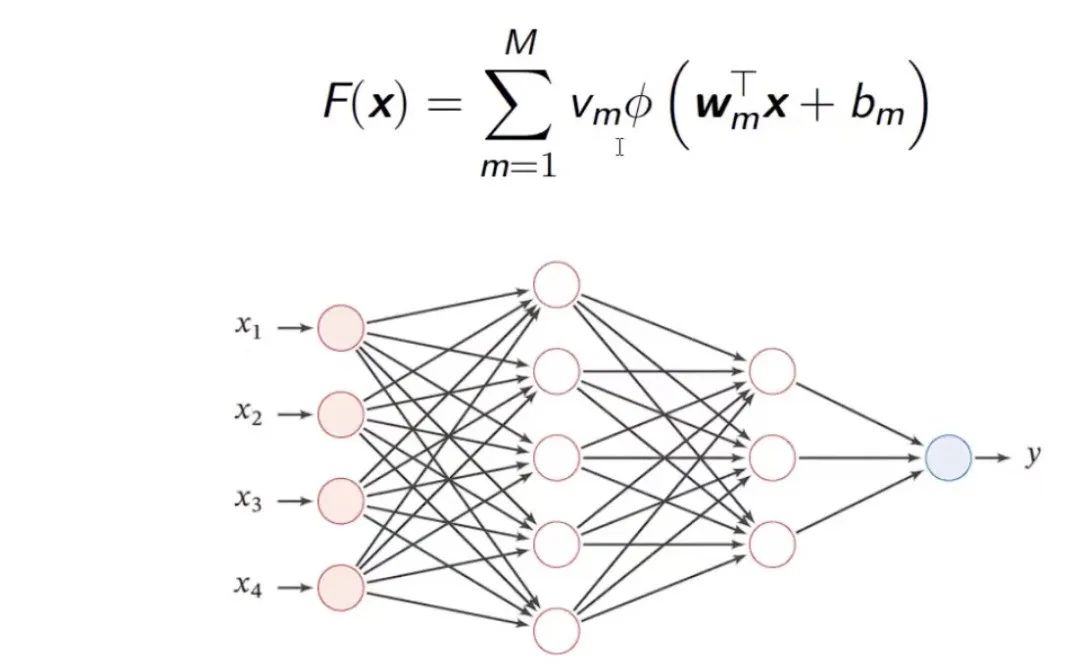
图：人工神经网络（Artificial Neural Network）

通用近似定理

在数学里，对于任何一个连续函数，总是可以找到一个多项式函数或者三角基数去逼近它。

然而，神经网络这一类特殊的函数在基础数学里并没有被广泛应用。尽管如此，计算数学领域已经使用神经网络来解决一些传统数学方法难以解决的问题。例如，使用神经网络去解决一些多尺度建模的问题。

2. 计算机辅助数学研究 

自人工智能诞生以来，探索 AI 在数学研究中的应用一直是一个重要的研究方向，并取得了许多重要成果。在符号主义的影响下，A. Newell 和 H. Simon 研发的“逻辑理论家“证明了《数学原理》中多条定理，这是符号主义的成功实践之一。而符号主义的另一重大成果，则是吴文俊先生开创的几何定理机器证明。吴先生利用代数几何，成功的将平面几何表述成一套精确的形式语句，从而可以借助计算机进行推理，实现平面几何定理的机器证明。

计算机辅助数学研究已经取得了一些令人瞩目的成就。例如，图论里经典的四色定理（任何平面上的地图只需要使用最多四种颜色来进行着色，以确保相邻的地区颜色不同）曾被计算机用穷举法证明。最近5年内，用神经网络辅助数学研究比较重要的工作包括：

• 符号回归寻找数学表达式：这种方法从数据中寻找精确的数学表达式，不仅仅是拟合数据，而是在给定的函数库内寻找函数，并通过组合和算术运算来生成一个函数，以拟合数据。这种方法已被用于发现物理学和数学中的精确公式。

• 强化学习构造猜想反例：利用强化学习，研究人员能够构造出猜想的反例，例如在图论中。这种方法可以用于验证某些猜想是否成立，从而发现新的数学性质。

• AI 辅助发现数学规律：通过AI辅助，研究人员已经建立了不同数学领域的规律，包括建立扭结不变量、发现新的矩阵乘法算法以及生成关于基本常数的猜想。这些工作突显了AI在数学研究中的重要作用。

2.1 符号回归寻找数学表达式

符号回归（symbolic regression）是一种从数据中寻找精确数学表达式的方法。与通用逼近理论不同，符号回归在给定一组输入和输出数据的情况下，试图找到一个函数来精确拟合这些数据。但这个函数是从一个事先定义好的函数库中选择的。这个库可以包含对数函数、三角函数、多项式函数等可能的函数。通过组合和基本算术运算，我们可以生成一个函数，以最好地拟合数据。

符号回归的重要性在于，它能够挖掘出物理学和数学中的第一性原理或精确公式，而不是像传统神经网络一样用一个近似的函数去逼近数据。这使得符号回归生成的函数具有可解释性。近年来，这种方法已被物理学家用于发现许多已知规律，如万有引力定律、爱因斯坦质能方程，以及费曼物理学讲义里很多已有的物理规律。然而，尚未通过这种方法发现未知的新规律，这可能是未来的研究方向。

就具体方法而言，符号回归方法可以通过向量化数学表达式来实现。它将数学表达式分解为单元，比如前缀表达式（即波兰表示法 Polish Notation，1920 年，波兰科学家扬 · 武卡谢维奇（Jan ukasiewicz）发明了一种不需要括号的计算表达式的表示法，将操作符号写在操作数之前）。类似于自然语言处理中把一个复杂的语句拆分成基本token的方法，一个复杂的数学表达式也可以被拆分成一些小token。然后，将token序列作为输入，使用机器学习模型进行训练，生成新的token序列，然后使用规则将其还原为数学表达式。

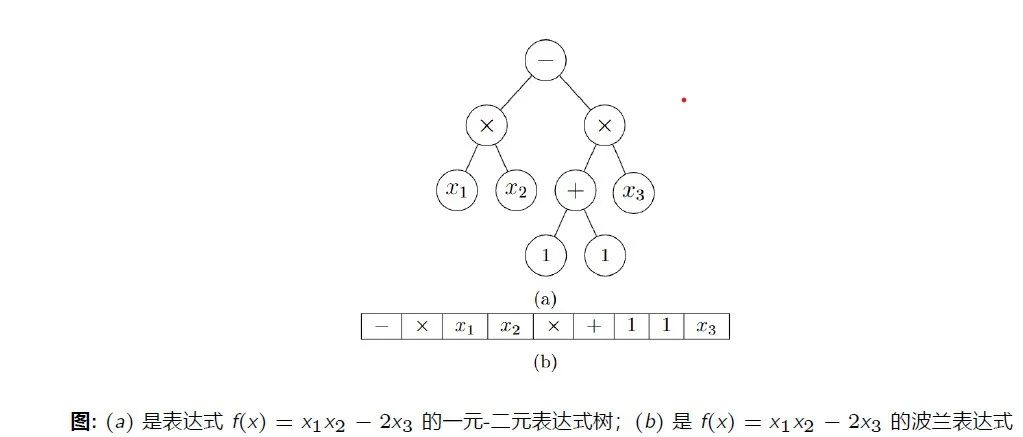
在训练方面，可以应用传统的机器学习方法，如线性回归、非线性回归、Transformer 架构、强化学习，或在网络结构中加入一些物理、数学或其他学科的先验知识来约束搜索空间。

图：各类方法的数学工具，表达式，参数集和搜索空间

（1）线性符号回归与非线性符号回归

线性符号回归（Linear SR）的目标表达式有m个组成部分，单个目标表达式就是m=1的情况。每个部分可以表示成一个函数的线性组合，而这些函数来源于事先设定的函数库里。优化的目标是学习每个线性表达式的系数。如果用监督学习的话，就定一个损失函数，然后最小化损失函数。

而非线性符号回归（Nonlinear SR）将深度神经网络中的激活函数替换成数学算子，从数据中学习数学表达式。

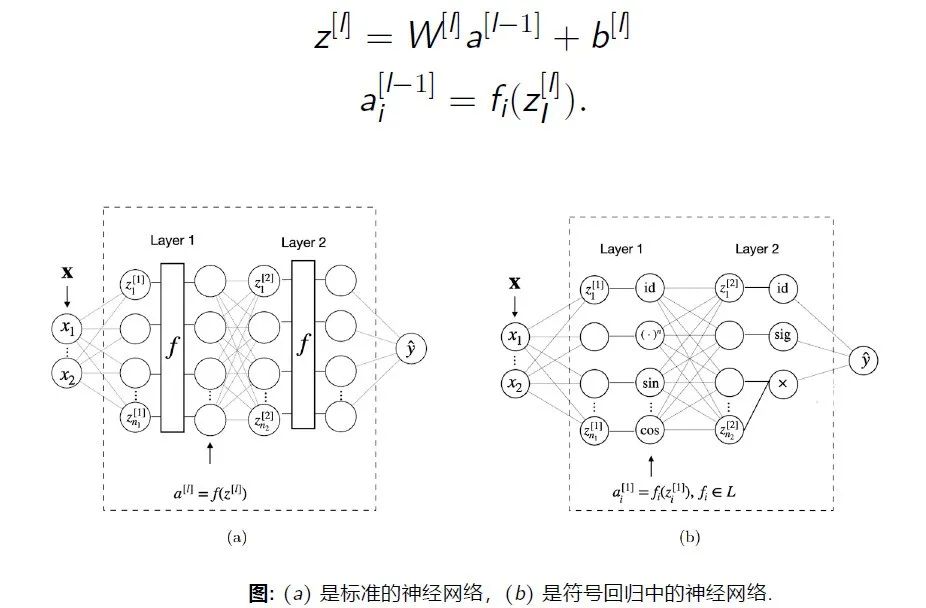
因此，符号回归与传统回归方法核心的不同在于，事先给定了函数库，然后在这个函数库里去选取函数进行线性或非线性的组合，再去优化参数。

（2）基于强化学习的符号回归方法：深度符号回归

Brenden K. Petersen, et al. Deep Symbolic Regression:Recovering Mathematical ExpressionsFrom Data Via Risk-Seeking Policy Gradients. ICLR 2021

基于强化学习的符号回归方法引入了智能体，即深度神经网络。按照数学公式的树表达式法，建立由一些数学符号构成的库，这样每个符号就编码成token，比如一个由四个符号构成的库，每个符号可以编码成一个 4 维的 one-hot 向量。通过约束搜索空间和优化常数，对符号表达式进行约束，例如限制表达式长度、表达式不能全是常数等。通过强化学习进行策略优化，最大化奖励函数来指导生成合适的数学表达式。

图：智能体（深度神经网络）生成树表达式

（3）物理启发的深度符号回归方法

Wassim Tenachi, et al. Deep symbolic regression for physics guided by units constraints: toward the automated discovery of physical laws. arXiv:2303.03192.

物理学领域也应用了深度符号回归方法。这些方法引入物理量纲约束，要求得到的方程必须在物理量纲方面保持平衡。这种方法已经用于发现爱因斯坦的质能方程等已知物理规律。

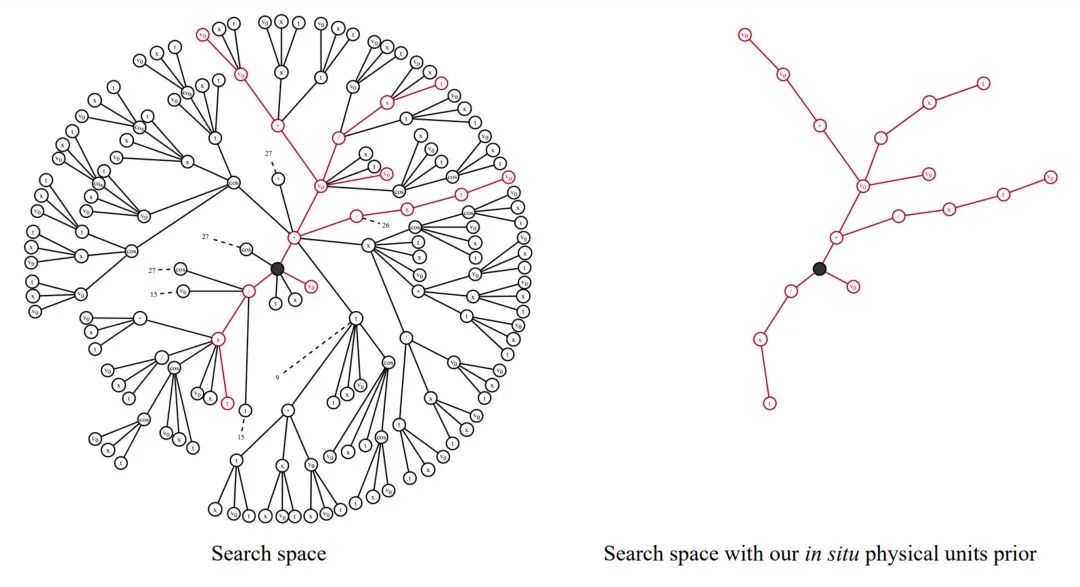
图：搜索空间

图：搜索空间被物理量纲约束

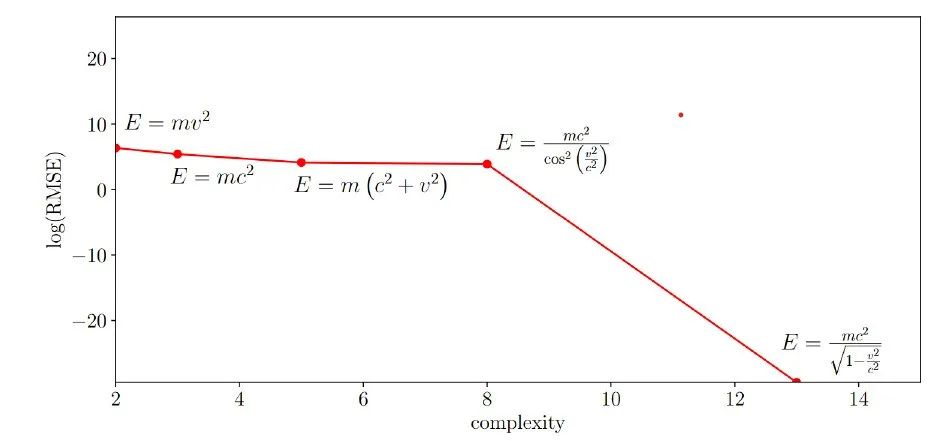
图：用物理量纲约束的深度符号回归寻找粒子的相对论能量

在物理学中，这种方法已被用于发现一些已知的方程，但对于一些未知的物理规律，目前还没有得出明确的结论。在数学领域，由于大多数基础数学研究者不太关注应用数学或神经网络，因此尚未广泛应用于发现定理。然而，理论上来说，这个方法有巨大的发展潜力，因为数学中的公式比物理中的多得多，而且不像物理那样需要通过实验验证，相对来说验证反馈时间较短。

2.2 强化学习构造猜想反例

Adam. Zsolt. Wagner . “Constructions in combinatorics via neural networks”.arXiv:2104.14516.

另一个令人激动的领域是使用强化学习构造猜想反例。以图论为例，先将图编码为邻接矩阵，然后将邻接矩阵转化为向量作为神经网络的输入，并根据环境反馈计算奖励，最后进行策略优化。

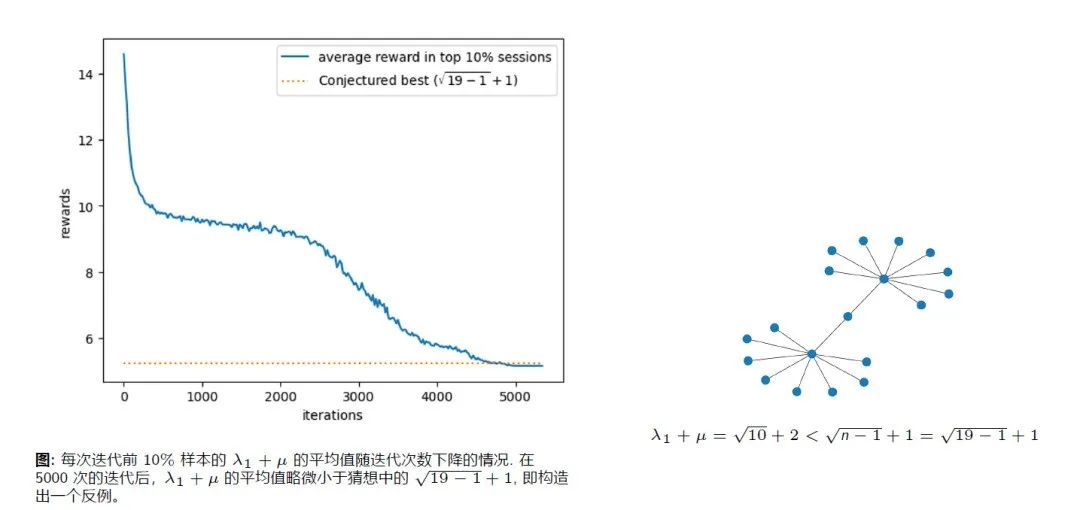
下面这个例子是图论里一个猜想，

作者用强化学习构造出了这个猜想的一个反例，生成了一个图，使得这个图不满足这个假设。构造反例的核心思想是让不等式的左边小于右边，所以奖励函数可以设置为负的左边表达式，然后最大化奖励函数。对于n<=18,  这个猜想是成立的。但当n=19时, 利用强化学习算法迭代，找到了反例。

2.3 AI 辅助发现数学规律

（1）AI 辅助建立扭结不变量间的联系

Davies. Alex, et al. “Advancing mathematics by guiding human intuition with AI. ” Nature 600 (2021): 70-74.

扭结是三维欧氏空间或者三维球面中的简单闭合曲线。为了区分两个扭结是否等价，即是否可以将一个扭结变形成另一个，人们引入了扭结不变量。扭结不变量有很多种，其中最著名的就是Jones Polynomial。为了探索不同的扭结不变量之间的关系，作者通过训练AI然后人工反馈从而找到一些规律。

具体来讲，模型训练了一个前馈神经网络来评估扭结的几何和代数不变量之间是否存在关系，根据随机采样的扭结数据集上的几何不变量来预测代数特征。为了了解网络是如何做出这一预测的，他们使用了基于梯度的归因技术来确定哪些几何不变量与代数特征最相关。通过人工反馈的方式，他们猜测到了这个不等式，然后进一步又在另一篇论文里严格证明了这个不等式。所以这项工作是AI辅助发现了数学定理。

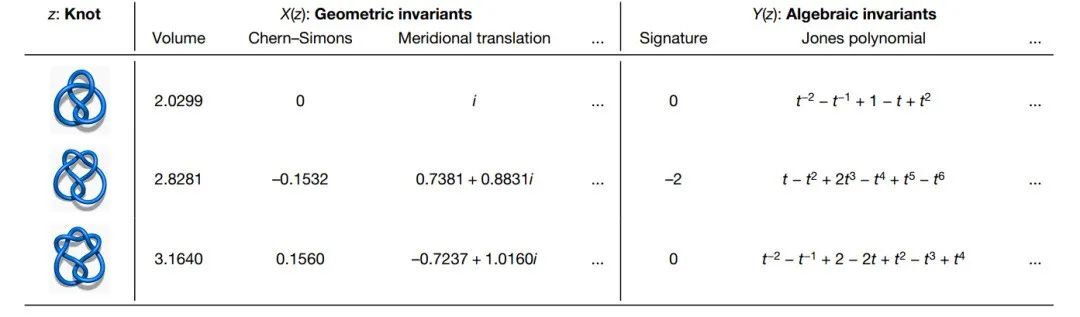
图：各种扭结及其对应的几何不变量与代数不变量

（2）AI发现矩阵乘法新算法

Fawzi. Alhussein, et al. “Discovering faster matrix multiplication algorithms with reinforcement learning”. Nature 610 (2022): 47-53.

在矩阵乘法领域，AI的应用也引人注目。研究人员发现了更快的矩阵乘法算法，通过强化学习将乘法运算次数降低到最低。比如，对于一个2*2的矩阵，标准的矩阵乘法要做8次乘法，而他们用强化学习寻找出一个新算法，把乘法运算减少到了7次。

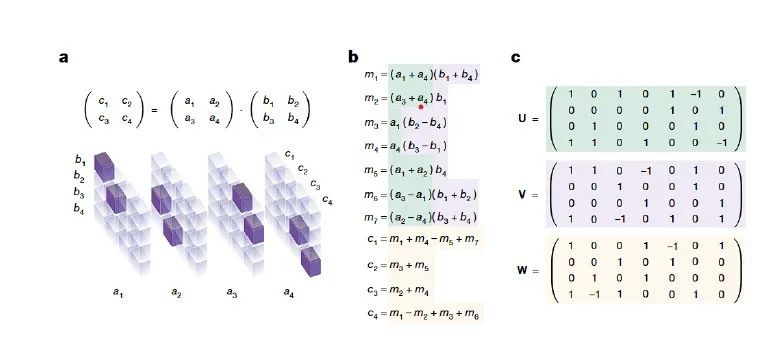
图：Strassen's algorithm 示意图，其中图a是三维情形的矩阵乘法的张量表征,  ai, bi, ci构成一个size为 (4,4,4) 的三维张量；图b展示了 Strassen’s algorithm 中使用的7个乘法；图c展示了将张量分解为7个秩为1的项的和

（3）AI生成关于基本常数的猜想

Gal Raayoni ,et al. Generating conjectures on fundamental constants with the Ramanujan Machine. Nature , 590 (2021): 67-73.

这项工作的核心思想是去寻找物理学或者数学里一些基本的常数的连分数的表示。

图：各种常数的连分数表示

值得注意的是，这个方法没有可推广性，因为它是为这个问题量身打造的。

3. 大语言模型在数学研究中的应用

近期人工智能大模型成为最热门的话题之一。作为语言大模型最具影响力的产品，ChatGPT引发了一场新的产业革命。

大语言模型的训练路线如下：

语言模型预训练 → 有监督指令微调 → 奖励模型训练 → 强化学习

大语言模型的思维链推理

Jason Wei, et al. Chain-of-Thought Prompting Elicits Reasoning in Large Language Models. arXiv:2201.11903 [cs.CL]

形式化的自动定理证明

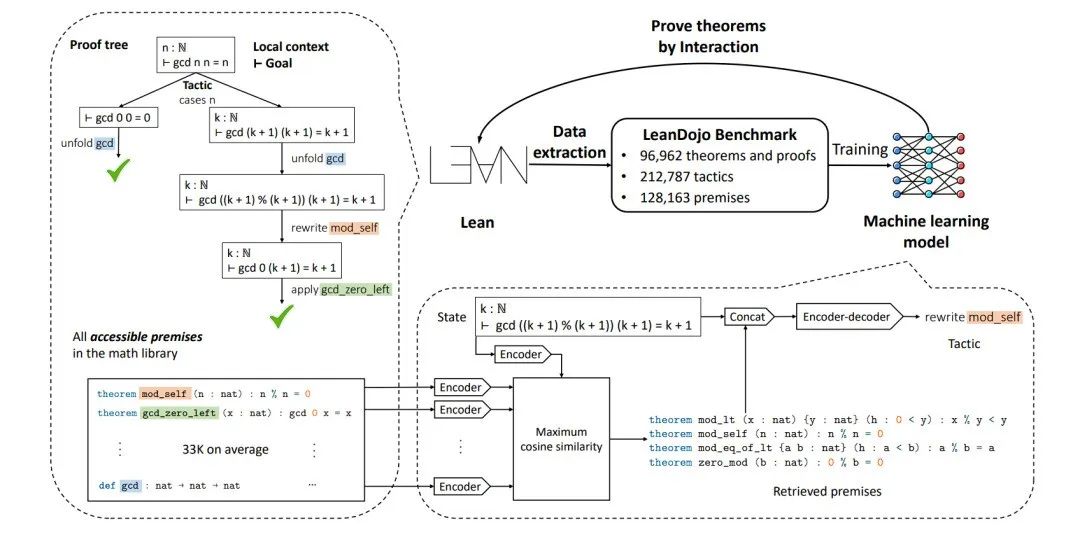
Kaiyu Yang et al. LeanDojo: Theorem Proving with Retrieval-Augmented Language Models. arXiv:2306.15626

这篇论文用大模型跟另外一套形式化的语言Lean去进行交互。Lean是一种形式化的语言，它将数学语言转化成计算机语言，然后在这个语言框架下去进行严格的推理。所以可以确保它的推理准确性比大模型要高。微软开发了Lean这个库，把很多数学知识变成了这种语言，涵盖上至本科数学的知识。LeanDojo基于已有的库，把计算机语言还原成自然语言，利用思维链 (chain-of-thought) 推理，把证明过程放到大模型里去训练，然后做微调，以提升大模型的能力。

4. 人机交互的数学研究平台

如何利用语言大模型，构建一个人机交互的数学研究平台？

数学研究大体分为两个过程：发现数学新命题，证明或证否数学命题。基于这两个基本过程，我们认为人机交互的数学研究平台应该包含如下基本组件：语言大模型 + 符号计算+ 符号回归 + 构造反例 + 自动证明。

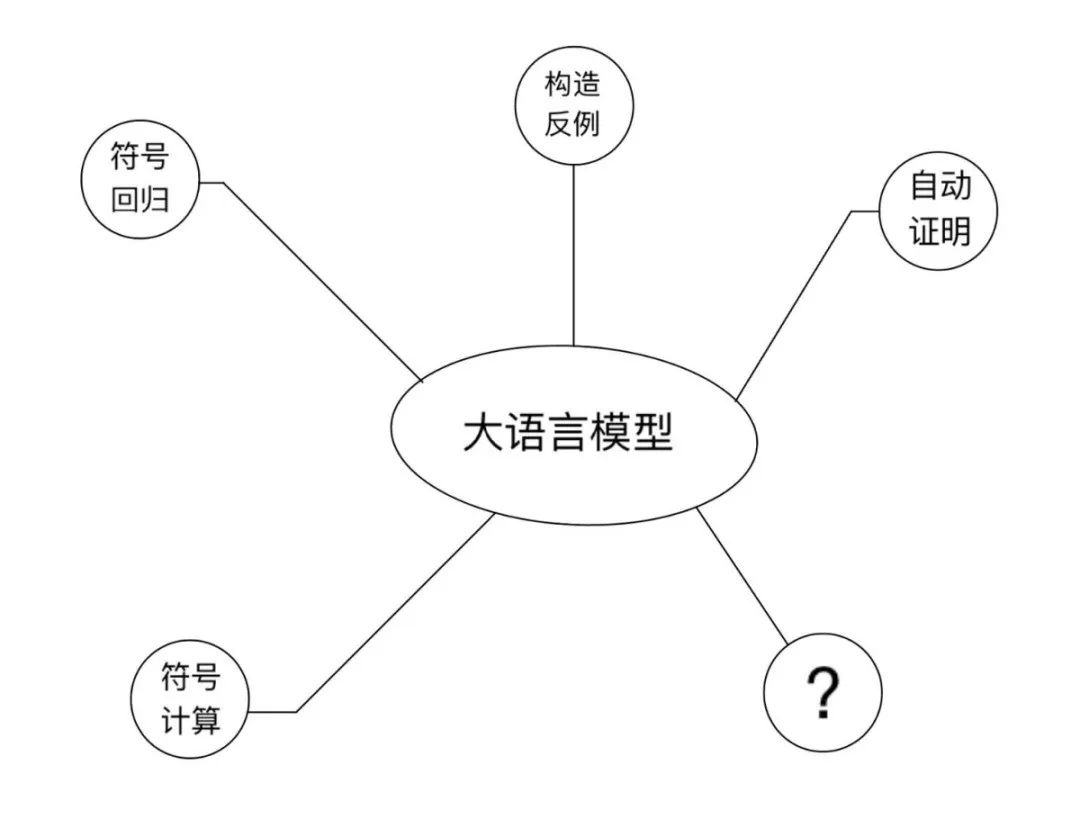
语言大模型已经逐渐成为人工智能时代的操作系统，也必将在人机交互的数学研究中发挥基础作用。在数学的发展历程中，许多重大猜想都是依赖数学其他分支的工具和思想得以证明的。由于语言大模型广泛的知识储备，数学家可以通过自然语言与计算机进行交互，整合全领域的数学知识，发现新的数学现象，并借助语言大模型的逻辑推理能力，实现数学命题的证明。然而，现阶段语言大模型在数学推理方面的能力仍然有所欠缺。如何搜集更多的专业数据并开发更强大的算法，改进现有语言大模型的数学推理能力是未来急需解决的重要问题。

在以上基本组件中，语言大模型是一个基础设施，其他组件作为插件部署并被调用。数学家可以借助该平台，通过自然语言与计算机进行交互，实现对数学命题更高效的发现，证明或证否。

经过几个月的努力，DeepMath 研究团队近日发布了 DeepMath 数学大模型，并正在构建人机交互的现代数学研究平台。模型已上传到 Huggingface，感兴趣的朋友可以登录 www.deepmath.cn 通过邀请码注册，在线体验实际效果。 

DeepMath 大模型的特点：

DeepMath 大模型基于 Llama2 微调，显著提升了大模型在现代数学知识问答的能力。为了验证模型效果，我们在线问了一个拓扑学问题：what is a compact topological space? 得到的答案是：A topological space X is compact if every open cover of X has a finite subcover. 回答相当准确！

而如果使用原始 Llama2，会得到怎样的回复呢? 可以参考如下测试结果的截图：

可以看出，尽管原始 Llama2 的回复比较详尽，但是结果并不准确。我们又测试了分析、代数等学科的问题，发现 DeepMath 大模型的效果都相当不错。那么，我们是怎么训练出这种效果呢？

答案还是在于高质量数据集的构建。我们耗费了数月时间人工标注了几千条现代数学知识问答指令，涵盖了微积分，实分析，复分析，概率论，泛函分析，抽象代数，微分方程，微分几何，拓扑学等多个方向。DeepMath大模型正是基于这个高质量的数据集监督微调而来。

为了增强语言大模型的计算能力，我们将 DeepMath 数学大模型与开源数学软件 Sagemath 结合起来。我们构建了一个 Sagemath 代码数据集，并与现代数学知识问答数据集结合，共同微调训练 Llama2，显著提升了模型使用工具与计算能力。

我们将陆续开发符号回归，构造反例，自动证明等组件，并基于AI智能体的思想，将所有组件有效组织起来，从而达到通过自然语言交互并调度各组件，实现对数学命题更高效的发现，证明或证否。

5. 展望：如何借助 AI 发现新的数学概念？

最后，陈小杨老师提出了几个未来AI和数学结合的发展方向：

• 数学对象如何向量化？我们讨论了函数表达式和图的向量化方法，但数学里还有很多其他的数学对象，比如代数结构（如群环域）、几何结构（如流形、代数簇），等等。如何将它们向量化还没有引起大家的关注。

•  怎么用AI发现新的数学概念？

•  如何将神经网络视为特殊函数，用于解决基础数学问题？

期待和更多朋友一起探索！

学者简介

陈小杨，同济大学特聘研究员。2014年5月获得美国圣母大学数学博士学位，2014-2016年在澳门大学从事博士后研究，并于2016年底入职同济大学。陈小杨的主要研究方向为黎曼几何，在 Geometry and Topology, Advances in Mathematics 等期刊发表了多篇研究论文。近期，陈小杨与研究团队开展了大模型在基础数学的应用研究，并计划开发机器学习算法用于发现数学规律，构造数学猜想反例等。

未来智能实验室的主要工作包括：建立AI智能系统智商评测体系，开展世界人工智能智商评测；开展互联网（城市）大脑研究计划，构建互联网（城市）大脑技术和企业图谱，为提升企业，行业与城市的智能水平服务。每日推荐范围未来科技发展趋势的学习型文章。目前线上平台已收藏上千篇精华前沿科技文章和报告。

  如果您对实验室的研究感兴趣，欢迎加入未来智能实验室线上平台。扫描以下二维码或点击本文左下角“阅读原文”