numpy函数_np. c

目录

1、np.c_和np.r_的用法解析

2、shape函数

3、ones函数

4、eyes函数

6、numpy.ceil()

7、linalg模块 

 7.1、创建矩阵

7.2、使用inv函数计算逆矩阵

7.3、求解线性方程组

7.4、np.linalg.det()

7.5、linalg.eig()

8、numpy.ravel() vs numpy.flatten()

9、Cumsum ：

10、arange

11、np.mean(data, axis=0)函数

12、numpy.reshape(a, newshape, order='C')[source]

13、array_split()函数

14、numpy矩阵数值提取

15、range

16、np.nonzero()

17、np.argsort()/argmax

---

 

---

---

1、np.c_和np.r_的用法解析

np.r_是按行连接两个矩阵，行数会变大，就是把两矩阵上下相加，要求列数相等。

np.c_是按列连接两个矩阵，列数会变大，就是把两矩阵左右相加，要求行数相等。

import numpy as np
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
c = np.c_[a,b]
 
print(np.r_[a,b])
print(c)
print(np.c_[c,a])
 
结果：
[1 2 3 4 5 6]
 
[[1 4]
 [2 5]
 [3 6]]
 
[[1 4 1]
 [2 5 2]
 [3 6 3]]

在numpy中，一个列表虽然是横着表示的，但它是列向量。

from：https://blog.csdn.net/yj1556492839/article/details/79031693 

2、shape函数

是numpy.core.fromnumeric中的函数，它的功能是查看矩阵或者数组的维数。返回元组类型。

import numpy as np
x = np.array([[1,2,5],[2,3,5],[3,4,5],[2,3,6]])
#输出数组的行和列数
print x.shape  #结果： (4, 3)
#只输出行数
print x.shape[0] #结果： 4
#只输出列数
print x.shape[1] #结果： 3

3、ones函数

    numpy.ones(shape, dtype=None, order='C')      ，  返回全是“1”的数组，矩阵的行列数由shape给出。

>>> np.ones(5)
 
array([ 1.,  1.,  1.,  1.,  1.])
 
>>> np.ones((5,), dtype=np.int)
 
array([1, 1, 1, 1, 1])
 
np.ones((2, 1))
 
array([[ 1.],
 
       [ 1.]])

4、eyes函数

>>> e = eye(3)  
>>> e  
array([[ 1.,  0.,  0.],  
       [ 0.,  1.,  0.],  
       [ 0.,  0.,  1.]])  
>>> e.shape  
(3, 3)

6、numpy.ceil()

 朝正无穷大方向取整

>>> a = np.array([-1.7, -1.5, -0.2, 0.2, 1.5, 1.7, 2.0])
>>> np.ceil(a)
array([-1., -1., -0.,  1.,  2.,  2.,  2.])

7、linalg模块 

numpy.linalg模块包含线性代数的函数。使用这个模块，可以计算逆矩阵、求特征值、解线性方程组以及求解行列式等。

 7.1、创建矩阵

A = np.mat("0 1 2;1 0 3;4 -3 8")
print (A)
#[[ 0 1 2]
# [ 1 0 3]
# [ 4 -3 8]]

7.2、使用inv函数计算逆矩阵

B = np.linalg.inv(A)
print (B)
 
[[-4.5 7. -1.5]
 [-2. 4. -1. ]
 [ 1.5 -2. 0.5]]
 
 检查原矩阵和求得的逆矩阵相乘的结果为单位矩阵
print (A * inv)
#[[ 1. 0. 0.]
# [ 0. 1. 0.]
# [ 0. 0. 1.]]
 
# 注：矩阵必须是方阵且可逆，否则会抛出LinAlgError异常。

7.3、求解线性方程组

numpy.linalg中的函数solve可以求解形如 Ax = b 的线性方程组，其中 A 为矩阵，b 为一维或二维的数组，x 是未知变量

#创建矩阵和数组
B = np.mat("1 -2 1;0 2 -8;-4 5 9")
b = np.array([0,8,-9])
 
# 调用solve函数求解线性方程
x = np.linalg.solve(B,b)
print (x)
#[ 29. 16. 3.]
 
# 使用dot函数求内积，就是矩阵乘法，检查求得的解是否正确
#两种使用形式
C=np.dot(B , x)
print (C)
# [[ 0. 8. -9.]]
 
 
C= B.dot(x)
print (C)
# [[ 0. 8. -9.]]

7.4、np.linalg.det()

     矩阵求行列式（标量）

7.5、linalg.eig()

   计算特征值与特征向量，

# 创建一个矩阵
C = np.mat("3 -2;1 0")
 
c1,c2 = np.linalg.eig(C)
print (c1)
# [ 2. 1.] 特征值
print (c2)特征向量
#[[ 0.89442719 0.70710678]
# [ 0.4472136 0.70710678]]

8、numpy.ravel() vs numpy.flatten()

       两者所要实现的功能是一致的（将多维数组降位一维,两者默认均是行序优先），两者的区别在于返回拷贝（copy）还是返回视图（view），numpy.flatten()返回一份拷贝，不会影响原始矩阵，而numpy.ravel()返回的是视图，会影响原始矩阵。

                         

9、Cumsum ：

     计算轴向元素累加和，返回由中间结果组成的数组，重点就是返回值是“由中间结果组成的数组”

9.1、对于一维输入

>>>import numpy as np
>>> a=[1,2,3,4,5]
>>> np.cumsum(a)
array([  1,   3,   6,  10,  15])

9.2、对于二维输入

axis=0(第1行不动，将第1行累加到其他行)；axis=1(进入最内层，转化成列处理。第1列不动，将第1列累加到其他列)，如下：

>>>import numpy as np
>>> c=[[1,2,3],[4,5,6],[7,8,9]]
>>> np.cumsum(c,axis=0)#行叠加
array([[ 1,  2,  3],
       [ 5,  7,  9],
       [12, 15, 18]])
>>> np.cumsum(c,axis=1)#列叠加
array([[ 1,  3,  6],
       [ 4,  9, 15],
       [ 7, 15, 24]])

9.3、对于三维输入

    axis=0 (第1行不动，将第1行累加到其他行)； axis=1(进入第2层，每个第二层第1行不动，累加到其他行)； axis=2(进入最内层，转化成列处理。第1列不动，将其累加到其他列)，注意维数从外到内是0-2编号，如下：

>>>import numpy as np
>>> a
[[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 20, 30]]]
>>> np.cumsum(a,axis=0)
array([[[ 1,  2,  3],
        [ 4,  5,  6]],
 
       [[ 8, 10, 12],
        [14, 25, 36]]])
>>> np.cumsum(a,axis=1)
array([[[ 1,  2,  3],
        [ 5,  7,  9]],
 
       [[ 7,  8,  9],
        [17, 28, 39]]])
>>> np.cumsum(a,axis=2)
array([[[ 1,  3,  6],
        [ 4,  9, 15]],
 
       [[ 7, 15, 24],
        [10, 30, 60]]])

a是一个 2 x 2 x 3 的 list，解释起来有点麻烦，先把 a 变种风格
[ //axis=0
             [//axis=1。同时是axis=0所对应的第 1 行，注意是此中括号包含的整个内容
                   [1, 2, 3], //axis=2。同时是 axis=1所对的第1行
                   [4, 5, 6] //axis=2
             ],
             [//axis=1。同时是axis=0所对应的第 2行
                    [7, 8, 9], //axis=2。同时是 axis=1所对的第1行
                    [10, 20, 30] //axis=2
             ],
     ]

axis=0说明，第1维度，包含2行，绿色中括号的list，第1行(也就是由1,2,3,4,5,6组成的list)不动，累加到第二行，注意是累加
axis=1说明，第2维度,  每个绿色中括号里第1行不变，也就是 [1,2,3]和[7,8,9]不动，累加到同兄弟行（同属一个中括号的行）
axis=2说明，第3维度，也是最内层，转化成列处理，加粗数字所在列不动，累加到其他列上

10、arange

 np.arange()函数返回一个有终点和起点的固定步长的排列。 (包含起点，不包含终点）
参数个数情况： np.arange()函数分为一个参数，两个参数，三个参数三种情况 
1）一个参数时，参数值为终点，起点取默认值0，步长取默认值1。 
2）两个参数时，第一个参数为起点，第二个参数为终点，步长取默认值1。 
3）三个参数时，第一个参数为起点，第二个参数为终点，第三个参数为步长。其中步长支持小数。

11、np.mean(data, axis=0)函数

     axis=0，那么输出矩阵是1行，求每一列的平均（按照每一行去求平均）；axis=1，输出矩阵是1列，求每一行的平均（按照每一列去求平均）。还可以这么理解，axis是几，那就表明哪一维度被压缩成1维。

import numpy as np
X = np.array([[1, 2], [4, 5], [7, 8]])
print np.mean(X, axis=0, keepdims=True)
 
结果是
 [[ 4.  5.]] 
               
print np.mean(X, axis=1, keepdims=True)
 
 [[ 1.5]
  [ 4.5]    
  [ 7.5]]

      再举个更复杂点的例子，比如我们输入为batch = [128, 28, 28]，可以理解为batch=128，图片大小为28×28像素，我们相求这128个图片的均值，应该这么写：batch对应第一维axis=0;

m = np.mean(batch, axis=0)
#输出结果m的shape为(28,28)，就是这128个图片在每一个像素点平均值。

12、numpy.reshape(a, newshape, order='C')[source]

      如果newshape等于-1的话，那么Numpy会根据剩下的维度计算出数组的另外一个shape属性值。

举几个例子，有一个数组z，它的shape属性是(4, 4)，z.reshape(-1)后将z变成  一行  数组

z = np.array([[1, 2, 3, 4],
          [5, 6, 7, 8],
          [9, 10, 11, 12],
          [13, 14, 15, 16]])
z.shape
(4, 4)
 
z.reshape(-1)
array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16])

z.reshape(-1, 1)

     我们不知道z的shape属性是多少，但是想让z变成只有一列，行数不知道多少，通过`z.reshape(-1,1)`，Numpy自动计算出有16行，新的数组shape属性为(16, 1)

z.reshape(-1,1)
 array([[ 1],
        [ 2],
        [ 3],
        [ 4],
        [ 5],
        [ 6],
        [ 7],
        [ 8],
        [ 9],
        [10],
        [11],
        [12],
        [13],
        [14],
        [15],
        [16]])
 

z.reshape(-1, 2)

    newshape等于-1，列数等于2，行数未知，reshape后的shape等于(8, 2)

 z.reshape(-1, 2)
 array([[ 1,  2],
        [ 3,  4],
        [ 5,  6],
        [ 7,  8],
        [ 9, 10],
        [11, 12],
        [13, 14],
        [15, 16]])
 

13、array_split()函数

array_split(rnd_idx, n_batches)：对于长度为l 的数组，应该分成n个部分，它返回  l％n（取余数）个    大小为l // n + 1（取整）的子数组和其余大小为l // n的子数组

 x = np.arange(8.0)
 np.array_split(x, 3)     #n=3，8//(3+1)=2,所以有2个是长度为指定为3长度，剩下的为一个长度
输出： [array([ 0.,  1.,  2.]), array([ 3.,  4.,  5.]), array([ 6.,  7.])]

A = np.arange(12).reshape(3, 4)
print A
 
# 纵向分割, 分成两部分, 按列分割
print np.split(A, 2, axis = 1)
# 横向分割, 分成三部分, 按行分割
print np.split(A, 3, axis = 0)
 
# Test 1 result
[[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]]
[array([[0, 1],
       [4, 5],
       [8, 9]]), array([[ 2,  3],
       [ 6,  7],
       [10, 11]])]
[array([[0, 1, 2, 3]]), array([[4, 5, 6, 7]]), array([[ 8,  9, 10, 11]])]
 
# Test 2
# 不均等分割
print np.array_split(A, 3, axis = 1)
 
# Test 2 result
[array([[0, 1],
       [4, 5],
       [8, 9]]), array([[ 2],
       [ 6],
       [10]]), array([[ 3],
       [ 7],
       [11]])]
In [5]:
 
# Test 3
# 垂直方向分割
print np.vsplit(A, 3)
# 水平方向分割
print np.hsplit(A, 2)
 
# Test 3 result
[array([[0, 1, 2, 3]]), array([[4, 5, 6, 7]]), array([[ 8,  9, 10, 11]])]
[array([[0, 1],
       [4, 5],
       [8, 9]]), array([[ 2,  3],
       [ 6,  7],
       [10, 11]])]

14、numpy矩阵数值提取

X = np.array (  [ [0, 1], [2, 3], [4, 5]  ]  )   #二维矩阵
 
X[:,0]就是取所有行的第0列数据
print(X[:, 0])#输出：[ 0  2  4  6  8 10 12 14 16 18]
print( X[:,1])#输出：[ 1  3  5  7  9 11 13 15 17 19]
 
#X[1,:]第1行所有值
print(X[1,:])#输出：[2 3]
 
#Y[:, m:n]，即取所有行的第m到n-1列数据，含左不含右
print (Y[1,:1])#输出：[ 2]
 
m=len(y)#y是向量
Y_one_hot=np.zeros((m,n_classes))
Y_one_hot[np.arange(m),y]=1   #就是在Y_one_hot的前m行按照y进行索引，y中的值不能超出Y_one_hot的列数。

                                   

15、range

多用作循环，range（0,10）返回一个range对象，如想返回一个list，前面加上list转换；arange是numpy模块中的函数，使用前需要先导入此模块，arange(3):返回array类型对象。

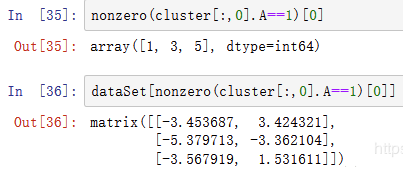
16、np.nonzero()

    当使用布尔数组直接作为下标对象或者元组下标对象中有布尔数组时，都相当于用nonzero()将布尔数组转换成一组整数数组，然后使用整数数组进行下标运算。

b1 = np.array([True, False, True, False])
>>> np.nonzero(b1)
    (array([0, 2]),)

     对于二维数组b2，nonzero(b2)所得到的是一个长度为2的元组。它的第0个元素是数组a中值不为0的元素的第0轴的下标，第1个元素则是第1轴的下标，因此从下面的结果可知b2[0,0]、b[0,2]和b2[1,0]的值不为0：

>>> b2 = np.array([[True, False, True], [True, False, False]])
>>> np.nonzero(b2)
    (array([0, 0, 1]), array([0, 2, 0]))

17、np.argsort()/argmax()

numpy.argsort(a, axis=-1, kind=’quicksort’, order=None) 
功能: 将矩阵a按照axis排序,返回值: 输出排序后的下标
>>> x = np.array([[1, 5, 7], [3, 2, 4]])
>>> np.argsort(x, axis=0)
array([[0, 1, 1],
       [1, 0, 0]])  #沿着行向下(每列)的元素进行排序

argsort()默认从小到大排序，argsort(-x),加负号之后，从大到小排序

>>> x = np.array([3, 1, 2])
>>> np.argsort(x)
array([1, 2, 0])
 
>>> np.argsort(-x)
array([0, 2, 1])

np.argsort()[num]的形式：

当num>=0时，np.argsort(x)[num]就可以理解为第num个最小数的索引;

当num<0时，np.argsort()[num]就是把从大到小的序号，反向输出，例如np.argsort()[-1]即输出x中最大值对应的index，np.argsort()[-2]即输出x中第二大值对应的index。