图像先验分布详解_先验知识权重函数

引子

图像复原是图像处理中最重要的任务之一，其包括图像去噪、去模糊、图像修复、超分辨等， 都是底层视觉中被广泛研究的问题。实际中我们得到的图像往往是退化后的图像（如带噪声图像、模糊图像、被采样的图像等）：
$$y=D(x)$$
其中，$y$表示观察到的退化图像，$x$是原始图像，$D(\cdot )$是退化函数，往往是未知的，在实际的计算中，常常使用成像物理模型近似。
一般有poisson模型和高斯模型：
$$Gaussian：y=Kx+b$$
$$Poisson:$$

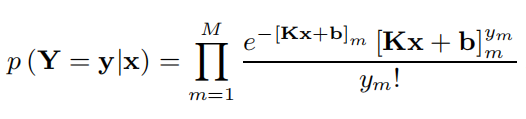
高斯是普通成像较为常见的模型，而荧光显微成像领域，则$Poisson$更为适合，因为应用科研级相机，高斯噪声很小，并且$Poisson$模型本身符合荧光成像。$Poisson$模型中$b$为背景而非$Gaussian$中$b$是噪声。
当然还有$Gaussian和Poisson$混合噪声模型。
图像复原就是根据观察到的退化图像，估计原始未退化的图像。这是一个病态问题，该问题的解往往不是唯一的。为了缩小问题的解空间，更好的逼近真实解，我们需要添加限制条件。这些限制条件来自自然图像本身的特性,即自然图像的先验信息。如果能够很好地利用自然图像的先验信息,就可以从退化的图像上恢复原始图像。

图像复原

图像复原任务通常表示成一个损失函数的形式：
$$x=argmi{n}_{x}f(x,y)+prior(x)$$
其中，$f(x,y)$表示数据保真项，使得估计出的原始图像与退化图像在内容上保持一致。$prior(x)$则表示先验项，来自于自然图像本身的特性。
这个损失函数可以从概率统计角度给予很好的解释。根据最大后验概率估计原理，对原始图像的估计可以表示为：
$$maxP(x|y)=maxP(y|x)P(x)$$
其中，$P(y|x)$表示从原始图像$x$得到退化图像$y$的概率，$P(x)$表示图像x的先验概率。对上式取负对数，就可以得到图像复原的损失函数了。

自然图像先验

借助于不同的自然图像先验信息，可以估计出不同的原始图像。常用的自然图像的先验信息有自然图像的局部平滑性、非局部自相似性、稀疏性等特征 。下面分别做简单介绍。

局部平滑性

自然图像相邻像素点之间的像素值在一定程度上是连续变化的。从频谱上观察，自然图像以低频分量为主；从梯度直方图上观察，自然图像梯度统计趋近于0。下图为Lena图的梯度直方图：

基于自然图像梯度统计的观察，许多先验条件都是针对图像梯度设计的，如梯度的$L_2$范数约束、TV约束（梯度L1范数约束）、梯度$L_0$范数约束等等，都是非常常见的。最常见的应用就是在去噪上，也就是基于全局优化的滤波器的设计。
梯度$L_2$范数约束是基于梯度统计服从高斯分布得到的，大名鼎鼎的最小权重滤波（WLS）便是基于此设计的，但是对梯度的L2往往在抑制噪声的过程中，将许多纹理也平滑掉了。TV约束是基于梯度统计服从拉普拉斯统计得到的，其对于噪声鲁棒性更好，对纹理细节的保留也优于$L_2$范数约束。梯度$L_0$范数约束比起TV约束更强调局部一致性（TV约束相较而言更强调局部平滑性）。除此之外，在图像去模糊中，还常用到超拉普拉斯先验，即认为梯度分布的范数在(0,1]之间，其更加符合对自然图像梯度统计的描述。

先验表示

$$梯度L_2范数prior(x)=\Vert \nabla {\Vert }_2^2$$
$$TV约束prior(x)=\Vert \nabla {\Vert }_1$$
$$梯度L_0约束prior(x)=\Vert \nabla {\Vert }_0$$
$$超拉普拉斯先验prior(x)=\Vert \nabla {\Vert }_{\alpha },0<\alpha \le 1$$

$L_1、L_2$是最常用的先验模型，所以以下对其展开描述：

$L_1、L_2$正则化来源推导

$L_1{L}_2$的推导可以从两个角度：
1.带约束条件的优化求解（拉格朗日乘子法）；
2.贝叶斯学派的：最大后验概率；
实际上都差不多。

1.1 基于约束条件的最优化

对于模型权重系数$w$的求解释通过最小化目标函数实现的，也就是求解：

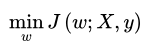
首先，模型的复杂度可以用VC（Vapnik-Chervonenkis Dimension）来衡量。它反映了模型的学习能力，VC维越大，则模型的容量越大。通常情况下，模型VC维与系数w的个数成线性关系：即：w数量越多，VC越大，模型越复杂。

为了限制模型的复杂度，我们要降低VC，自然的思路就是降低w的数量，让w向量中的一些元素为0或者说限制w中非零元素的个数。我们可以在原优化问题上加入一些优化条件：

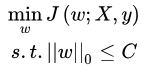
其中约束条件中的$||w|{|}_0$是指$L_0$范数，表示的是向量w中非零元素的个数，让非零元素的个数小于某一个C，就能有效地控制模型中的非零元素的个数，但是这是一个NP问题，不好解，于是我们需要做一定的“松弛”。为了达到我们想要的效果（权重向量w中尽可能少的非零项），我们不再严格要求某些权重w为0，而是要求权重w向量中某些维度的非零参数尽可能接近于0，尽可能的小，这里我们可以使用$L_1{L}_2$范数来代替$L_0$范数，即：

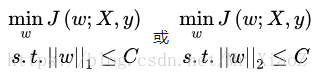
注意：这里使用$L_2$范数的时候，为了后续处理（其实就是为了优化），可以对进行平方，只需要调整C的取值即可。然后我们利用拉式乘子法求解：

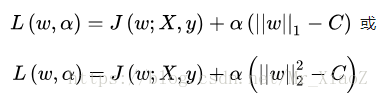
其中这里的是拉格朗日系数，$\alpha >0$，我们假设的最优解为${\alpha }^{\ast }$，对拉格朗日函数求最小化等价于：

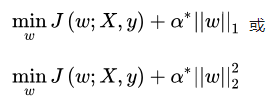
上面和

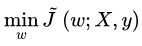
等价。所以我们这里得到对$L_1{L}_2$正则化的第一种理解：
$$L1正则化\rightleftharpoons 在原优化目标函数中增加约束条件{\Vert w\Vert }_1\le C$$

$$L2正则化\rightleftharpoons 在原优化目标函数中增加约束条件\Vert w\Vert {}_2^2\le C$$

1.1 基于最大后验概率估计

在最大似然估计中，是假设权重w是未知的参数，从而求得对数似然函数（取了$log$）：

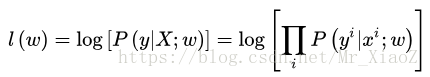
从上式子可以看出：假设$y^i$的不同概率分布，就可以得到不同的模型。

若我们假设：

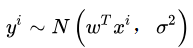
的高斯分布，我们就可以带入高斯分布的概率密度函数：

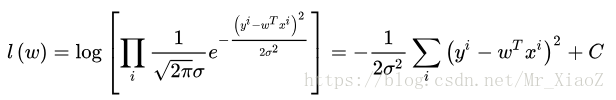
上面的C为常数项，常数项和系数不影响我们求解$max(l(w))$的解，所以我们可以令

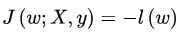
我们就得到了$LinearRegursion$的代价函数。

在最大化后验概率估计中，我们将权重w看做随机变量，也具有某种分布，从而有：

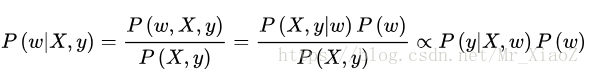
同样取对数：

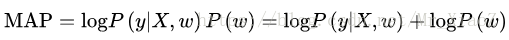
可以看出来后验概率函数为在似然函数的基础上增加了$logP(w)，P（w）$的意义是对权重系数w的概率分布的先验假设，在收集到训练样本$X，y$后，则可根据w在$X，y$下的后验概率对w进行修正，从而做出对w的更好地估计。

若假设的先验分布为0均值的高斯分布，即

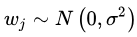
则有：

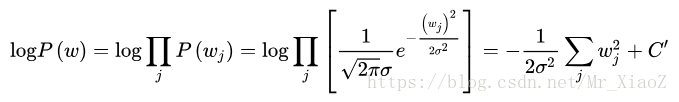
可以看到，在高斯分布下

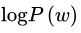
的效果等价于在代价函数中增加L2正则项。若假设服从均值为0，参数为a的拉普拉斯分布，即：

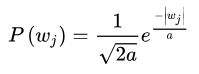
则有：

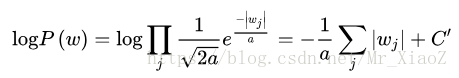
可以看到，在拉普拉斯分布下$logP(w)$的效果等价在代价函数中增加$L_1$正项。

故此，我们得到对于$L_1，L_2$正则化的第二种理解：

$L_1$正则化可通过假设权重w的先验分布为拉普拉斯分布，由最大后验概率估计导出。

$L_2$正则化可通过假设权重w的先验分布为高斯分布，由最大后验概率估计导出。

非局部相似性

在自然图像的不同位置，存在相似的纹理，且许多自然图像自身的纹理存在规律性。这说明自然图像本身信息是冗余的，我们可以利用图像的冗余信息对图像缺失或被污染的部分进行修复。

利用图像非局部相似性首先要找到图像中相似的纹理，最常用的方法是块匹配，即把图像分解成一个一个的小块，每个小块看作是一个单元，在图像中寻找与其相似的一个或多个小块。最经典的块匹配方法当然非Barnes的PatchMatch方法莫属。比起一个小块一个小块去比对，PatchMatch提供了一种近似的方法可以快速找到相似块。
现在主流的去噪方法和图像修复方法都是基于图像的非局部相似性。在去噪方面，非局部均值（non local mean，NLM）是利用非局部相似性去噪的开山之作。在此基础上发展而来的BM3D是应用最广泛，也是效果最好的去噪方法之一。关于这两种方法的介绍可以参见这篇博客。后面在NLM基础上也出现了一系列的改进方法，如将非局部相似性与低秩方法结合借来的WNNM，MCWNNM等去噪方法都取得了不错的效果。
在图像修复方面，块匹配方法在单帧图像缺失部分的修补方面占据了半壁江山。除此之外，还有基于Graph Cut进行图像修复的方法。但无一例外，所有这些方法都是利用了图像的非局部自相似性。关于图像修复可以参见这篇文章对这些方法的概述。另外，这篇文章还提到了一个有意思的观察，即自然图像中相似块之间的偏移量集中在少数几个偏移量上，这也从而说明了自然图像的纹理分布是存在一定周期性规律的。

稀疏性

稀疏性本身是指矩阵或向量中非零元素个数很少。对于自然图像来说，就是其可以用少量的几个独立成分来表示。即图像可以通个某些线性变化变成稀疏信号。图像的稀疏性是图像可以用压缩感知方法进行恢复的先决条件。
压缩感知进行图像恢复的过程如下图所示，图像经过线性基变换$\Psi$可以变成稀疏向量$S$。对原始图像进行随机采样可以得到观测向量$y$。利用观测向量$y$和恢复矩阵$\Theta$（常常是冗余字典）可以恢复出原始图像。

统计特性

统计特性是通过对大量图像进行学习得到的统计规律。这种特性比较抽象，一般对图像进行概率分布建模，将统计特性融合在概率模型的求解的参数里。一个比较常见的例子是EPLL先验（Expected Patch Log LIkelihood），其使用混合高斯模型从大量自然图像块中学习到先验知识。
基于监督模型的深度学习方法也是利用神经网络去自学习自然图像中的统计特性。

Deep image prior【题外话】

这是CVPR2018的文章。其也是通过神经网络获取图像先验，只不过与上面提到的用神经网络学习大量图像中的统计特性不同，deep image prior认为神经网络本身就是一种先验知识，网络自身结构限制了解的范围。网络会从退化图像中提取特征以用于退化图像的复原，且从结果可以看到，网络会先学习到图像中“未被破坏的，符合自然规律的部分”，然后才会学会退化图像中“被破坏的部分”。

Deep Image Prior类似于自然图像的非局部自相似性。关于Deep Image Prior的介绍可以参见这里。

参考：

1. https://www.jianshu.com/p/ed8a5b05c3a4
2. http://www4.comp.polyu.edu.hk/~cslzhang/paper/IR_lecture.pdf
3. http://www4.comp.polyu.edu.hk/~cslzhang/paper/SPM_IR.pdf
4. https://blog.csdn.net/zbwgycm/article/details/81187774
5. https://blog.csdn.net/m0_38045485/article/details/82147817