如何理解与学习数学分析——第二部分——数学分析中的基本概念——第9章——可积性

第2 部分：数学分析中的基本概念

(Concepts in Analysis)

9. 可积性(Integrability)

本章讨论了可积性(integrability)的概念(它不同于积分过程)。研究了反导数(antiderivative，或称原函数)和函数图像下面积之间的关系，然后通过对面积的近似建立了可积性的定义。给出了一个不可积函数的例子，并展示了如何在证明中使用Riemann条件(可积性验证)。最后解释了微积分基本定理。

9.1 何谓可积性(What is integrability)?

本章是关于可积性的(integrability)，而不是关于积分的(integration)。这是因为，正如第 3.3 节所讨论的，分析是关于早期数学的基础理论。对于可积性，这可能并不明显。关于积分，你可能受教的是——积分是反微分(微分的“对立面”)。这没错(尽管最好说微分和积分是互逆的运算)。你还可能被教授积分是关于求取函数图像下的面积。这也没有错。但它留下了很多问题。

首先，为什么微分和积分应该是逆运算？为什么求梯度或斜率与求函数图像下的面积“相反”？(注：如前几章所述，英国人使用“梯度(gradient)”一词，而美国人使用“斜率(slope)”一词来表示相同的意思。) 如果老师这么说，而你相信了，那也无妨。但如果你从未认真考虑过这种关系，那么现在就应该考虑一下。许多人在认真考虑时都认为这很惊人。梯度和面积究竟为什么会相关？它们似乎涉及完全不同的概念。但数学不是任意的——这种关系的存在不是因为某些权威随意规定它应该存在——所以一定有原因。而原因不明显这一事实意味着，一定有一些深奥的数学知识需要学习。

在另一方面，早期对微分和积分的研究通常涉及由单个公式定义的简单函数。但第 7 章和第 8 章介绍了具有更复杂规范的函数，这提出了微分和积分可能并不总是以无问题的方式进行互逆运算的可能性。例如，考虑下面显示的函数(您很快就会明白为什么我使用 t 作为变量而不是 x ) (注：这是明确的，因为由f (t) = 3t 给出的函数与由 f (x) = 3x 或 f (j) = 3j 或此模式的任何其它变量给出的函数是完全一样的。我们经常使用标准字母来表示标准事物，因为它可以帮助每个人更快地掌握新的思想，但如果有充分的理由使用不同的符号，我们不必坚持使用特定的符号。)

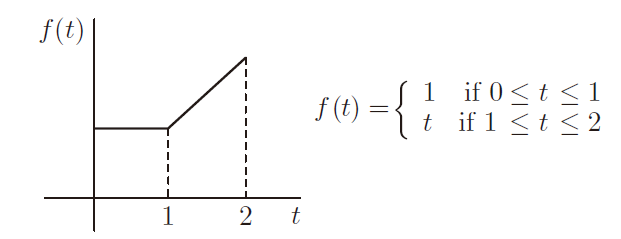
此函数在 t = 1 时不可微。因此，在这种情况下，积分不能直接与微分“相反”。不过，讨论 0 和 2 之间或 0 和一般点 x ∈ [0, 2] 之间的函数图像下面积似乎是合理的。可以使用下图和公式计算该面积(为什么我用 t 而不是 x ？)。想象一下 x 在轴上滑动，并使用简单的几何图形来验证公式是否有效。

 

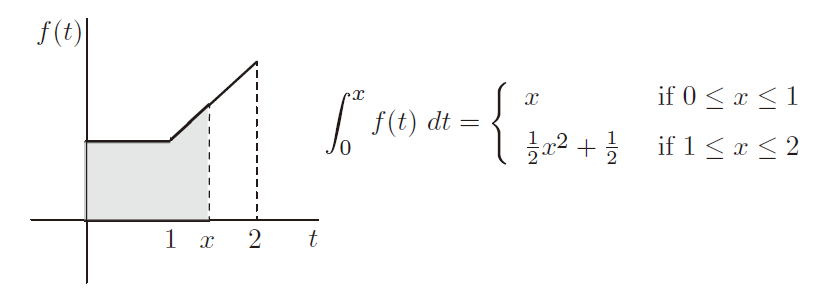
这个结果与函数 f 的直接公式积分有何关系？试试看。许多学生认为分段定义的函数可以通过简单地积分两个部分来实现积分，但事实并非如此。如果你读过第 8.6 节，你就会知道，这样的函数在“连接”处可能不可微；这个函数的分段性质不会破坏可积性，但我们确实需要谨慎对待积分常数。

         然而，有些函数的可积性是一个问题，比如这个：

许多人都认为，考虑这个函数的“函数图像下的面积”是没有意义的。所以我们应该期待一个可积性定义，将这个函数归类为不可积。我们将在第 9.5 节中验证这一点。

9.2 面积和反导数(Areas and antiderivatives)

         在定义可积性之前，我想先解释一下反导数和函数图像下面积之间的关系。我们倾向于谈论一个函数有“一个”反导数，比如 “   的反导数是    ”。但这不是单个函数，而是无限函数族，每个 c 值都有一个函数。这也许是件好事，因为在特定的图像下，不仅仅只有一个面积(译注：可能存在多个面积)——从 a 到 x 的函数图像下的面积通常不会与从另一个数 b 到 x 的函数图像下的面积相同：

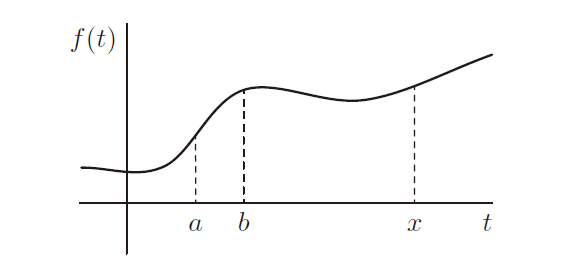
那么，不定积分(译注：或反导数)和面积到底如何结合起来呢？你可能以前想过这个问题，但许多分析专业的新生在计算上花费的时间比在概念理解上花费的时间多，因此他们无法给出好的答案。现在暂停一下，看看你是否可以，然后继续阅读。

         为了理清这种关系，我们首先要求得面积。例如，考虑由 f (x) = 3x  给出的简单函数 f ：ℝ ⟶ ℝ ，其中从 0 到一般点 x 的积分只是三角形的面积：

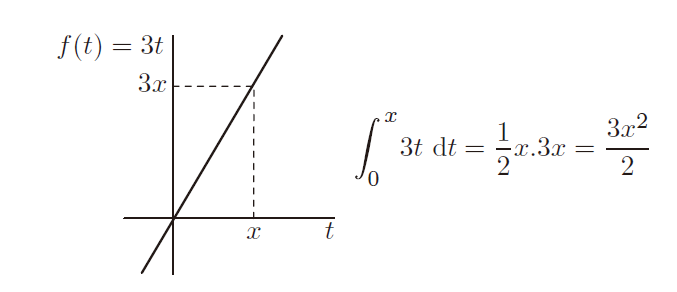
因此，积分与我们使用反导数求得的结果相符。但是求取面积仅会给出一个反导数——常数恰好等于 0 的那个(译注：反导数和求取面积的区别)。如果我们不是从零开始，而是在另一个固定数 a 和可变数 x 之间对f 进行积分，会发生什么？为了简单起见，让一切都保持正数，并且 x > a，得到以下结果：

 

 

从 a 开始而不是从 0 开始会切掉一点面积。但是这部分被切掉的面积是固定的，因此其表现出来的效果就是通过一个常数调整积分(如果 a 为负，会发生什么？)。这解释了为什么反导数应该是一组仅相差一个常数的函数。

         另一种方法是思考 x 动态变化时会发生什么。从定点  移动到定点  就增加了一个确定的面积(译注：指的是不定积分中的常数)——无论我们从哪里开始，我们总是收集这两定点之间相同数量的面积(译注：应指从  之前任意位置扫过这两点，这两定点之间的面积不变)。这意味着在任何特定点，增长面积的变化率都是固定的。行进速率并不在任何地方都相同——在下图中，  和  之间增加的面积大于    和  之间增加的面积。但  处的变化率是一个有意义的量，   处的(更大)变化率也是如此。

 

这意味着我们不仅可以考虑函数图像下的面积，还可以考虑该面积相对于 x 的变化率。当然，变化率是使用导数建模的。因此，面积和导数应该紧密相关，这开始变得合理。在建立适当的定义后，我们将在第 9.8 节中确切说明如何建立这种关系。

        

9.3 近似面积(Approximating areas)

第 9.2 节中的图形下的面积具有简单的形状，我们希望能够处理更复杂的函数，包括具有曲线图的函数。如果您首先想到的是我们应该使用积分，那则请小心。这会导致循环论证，因为它相当于说我们通过计算面积来找到积分，我们通过计算积分来找到面积。因此，从哲学上讲，理清面积测量问题很重要，并认识到尽管我们对讨论函数曲线图下的面积的含义有直观的认识，但获得该面积的数值测量并不是一件容易的事——它不能通过简单的乘法来完成。

数学家通过近似的方法来解决面积计算问题。对于  ，他们考虑如下图所示的估算值，其中矩形的总面积提供了一个低估(左侧)和一个高估。

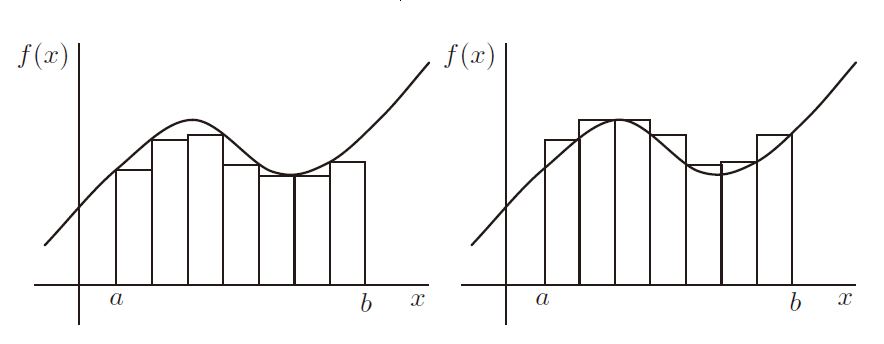
越窄的矩形(通常)能给出越接近的近似：

 

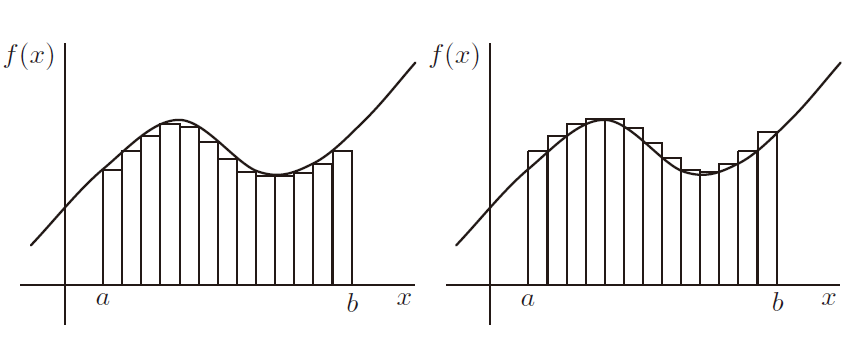
并没有哪个近似值可以给出准确的面积，但其思想是，如果低估和高估都可以尽可能地接近某个特定数 A，那么 A 就是函数图像下的面积。类似的推理在分析中随处可见——我们考虑尽可能地接近极限值。在这里，这让我们摆脱了哲学上存在问题的循环推理：数学家从有意义的区域(矩形的区域)开始，并使用它们来定义具有弯曲边缘的形状的面积的含义(注：您可能知道更复杂的近似积分方法，例如使用梯形法测(trapezium rule)或Simpson法则。但使用矩形的方法在代数上更简单，而且效果很好，所以这可能是您在分析中首先遇到的方法)。

    大多数学生发现，用矩形和近似值进行这种工作在直觉上是合理的。所以我们需要做的就是将其规范化。不幸的是，这样做需要引入大量符号，这意味着许多学生最终认为可积性很难。但这并不难。事实上，早期的可积性工作在逻辑上比早期的连续性工作更简单(例如)。所以我希望说服你，符号只是体现了上面概述的直观思想。

    规范化的第一步是考虑受限域上的可积性。如果你读过第 7 章和第 8 章，你就不会感到惊讶——连续性和可微性都是首先在某个点上定义的。讨论某个点上的可积性是没有意义的，但同样的一般思想也适用，因为存在一些函数在数轴的某些部分可积，但在其他部分不可积。所以数学家通常将函数描述为在区间[a, b]上可积或不可积。建立这一点后，策略是构造：

• 如何分割区间 [a, b]的表达式；

• 单个矩形面积的表达式；

• 单个高估的表达式，正式地称为上和(您认为低估叫什么？)；

• 通过将面积 A 与上和关联来指定面积 A 的表达式；

• 区间可积性的定义。

每个步骤都会引入符号，学生有时会感到困惑，因为他们无法理解某个步骤或混淆了两个步骤。在范范化之后，我将重复列表，以便您可以复习整个构造。

        

9.4 可积性定义(Integrability definition)

分割区间 [a, b] 通常涉及将最左边的点标记为  ，然后以显而易见的方式标记其他点并将最后一个点标记为  。您可能会看到下面的定义；在附图中，n = 5，矩形的总面积给出了与分区  相关的高估。

定义：集合 [a, b] 的一个分割是点  的使得   的一个有限集。(注：你会惊讶地发现，有多少人在考试时因错把“一个有限点的集合”写成了“点的一个有限集合”而丢了分。所有点都是有限的，所以前者实际上什么也没说。一如既往，要注意细节。)

分割的定义是否指定所有子区间都具有相同的宽度？不。您经常会看到数学论证使它们相等，但这只是为了计算方便。

    求矩形的面积很简单。第一个矩形的宽度为   ，并且始终如此。在上图中，它的高度恰好是  ，但不一定总是如此——看看其他一些矩形就知道为什么了。对于一般子区间   ，高度是子区间上 f (x) 的最大值(注：这假设函数在子区间上确实具有最大值，这意味着函数必须有界。有时有界性的要求被纳入与可积性相关的定义中)。 我们经常给这个高度起个名字，比如

令   。

这里的“sup”是 supremum 的缩写，因此可以大声读作“ 让 等于   和     之间 x 的 f (x) 值的上确界”。 上确界的定义可以在第 10.5 节中找到；在这里，您可以继续非正式地将   视为子区间  上 f 的最大值，尽管这相对于定义来说有点不精确(阅读第 10.5 节以了解原因)。无论如何，第一个矩形的面积是  。您会在图表的垂直轴上标记  和  的位置在哪里？其他矩形的面积是多少？为什么  的定义使用“≤”符号而不是“<”符号很重要？

求得矩形面积之后，我们希望把它们加起来以获得对  的高估。高估用 “U(f；P)”表示，可以大声地读作“f关于分割P的上和(upper sum)”,其求取公式为(注：“Σ”是大写的希腊字母“sigma”)：

 。

请记住，当你看到 “Σ” 符号时，通常最好将表达式完整地写出来(译注：仅限于项数比较少的情况)。对于我们的图像，这给出了预期的总和

 。

低估的等价一般表达式为：

 。

“inf”是“infimum”(下确界)的缩写(同样，参见10.5节)。

    这种东西的符号略有不同；例如，你的老师或教科书可能会使用不同的符号来表示 U( f；p )。此外，也可以用不同的方式指定矩形。但原理总是相似的，所以你应该能够弄清楚这些思法(以及本章中的其他思想)是在你的课程中是如何用任何变体体现的。

    无论如何，这些定义都指定了一个上和或一个下和。而一个上和只是一个数；该公式体现了大量计算，但它得出一个总面积。跟踪这一点很重要，因为有许多不同的可能分割，每个分区都有自己的上和。也许一个上和是 17，另一个是 18，另一个是 18.5，等等。这些上和都是函数图像下面积的近似值，但该面积与它们有何关系？首先，积分 A 将小于或等于每个上和。其次，积分是所有可能上和集合的最大下限，也称为上和的最小值(同样参见第 10.5 节)：

A = inf { L( f；P )|P是[a, b]的一个分割}

A 应该与所有下和怎样关联以及我们应该记为什么？

    最后，所有这些推理都假设面积 A 是有意义的。但仅当无论我们使用下和还是上和进行计算都能得到相同的 A 值时，这些推理才有意义。因此可积性的定义是：

定义：对于定义于闭间 [a, b] 上的函数 f ，当且仅当

         inf{ L( f；P )|P是[a, b]的一个分割} = sup{ L( f；P )|P是[a, b]的一个分割}

时，则称其可积。

    总结本节，以下是承诺的构造列表的回顾。你能画出图表并重建所有表达式而无需查看吗？

• 如何分割区间 [a, b]的表达式；

• 单个矩形面积的表达式；

• 单个高估的表达式，正式地称为上和(您认为低估叫什么？)；

• 通过将面积 A 与上和关联来指定面积 A 的表达式；

• 区间可积性的定义。

9.5 一个不可积函数(A non-integrable function)

    在第 9.1 节中，我发现讨论下图中函数的图像下方面积似乎没有意义(该图像无法准确绘制，但如第 7.3 节所述，虚线提供了一些直觉)。

本节解释此断言与正式定义的关系。在继续阅读之前，请尝试通过思考如何定义可积性来预测论证。在哪一步我们会遇到麻烦？

         为了考虑可积性，我们需要一个区间 [a, b](我们假设 a ≠ b)。假设我们用分割  将区间拆分。上下和分别是什么？上和定义为  

  ,

并且每一个子区间都包含比率数(rational number)，因此，每一个  一定等于 1 (译注：根据定义，这个高度就是f (x) 在该点的函数值)。这意味着当我们展开 U( f；P )的时候，很多项就抵消掉了：

 。

因为这个分割并无特别之处，每一个其它分割都会产生上和(b - a),因此上界和的最小界是 (b - a) 。用符号表示，

            inf { L( f；P )|P是[a, b]的一个分割} = b - a  。

f 关于P 的下和定义为

 。

这一次，每一个  一定等于 0 。为什么？为什么这意味着

inf{ L( f；P )|P是[a, b]的一个分割} = 0 ？

最后，从可积性定义的角度来看，这一切意味着什么？上和的下确界是 (b - a)，下和的上确界为零，因此

inf{ L( f；P )|P是[a, b]的一个分割}≠ sup{ U( f；P )|P是[a, b]的一个分割} 。

这意味着，f 在[a, b]上不可积。

您是否认为可以使用类似的论证来证明每个非连续函数都一定不可积？如果函数仅在一个点不连续会怎样？我们将在下一节中讨论这种情况。

9.6  Riemann条件(Riemann’s condition)

如果您的课程对可积性的定义如上所述，则定义可能不仅会说“f 是可积的”，还说“f 是Riemann可积的”(注：“Riemann”是一个德国名字，因此读作“Reeman”)。这反映了这样一个事实：还有其他定义可积性和积分的方法。这些方法往往出现在更高级的课程中，因此我不会在这里讨论它们，但我确实想提请您注意其他以Riemann命名的东西。

定理(Riemann条件)：对于函数 f ，当且仅当对于每一个ε > 0 ,都存在 [a, b]的一个分割P ，使得 U( f；P ) - L( f；P ) < ε ，则其在[a, b]上是(Riemann)可积的。

表达式 “U( f；P ) - L( f；P )” 是上和与对应的下和之差，其在下图中表示为灰色框的总面积。

非正式地说，Riemann条件表明，对于某个函数，当且仅当通过考虑不同的分割，我们都可以将这个差最小化到我们想要的程度时，这个函数才是可积的。我不会在这里证明Riemann条件是有效的——尽管你应该考虑它与定义的关系——但我将说明如何应用它，并强调人们在考虑上和与下和时有时会忽略的一个细节。考虑如下具体的函数  f ：[0，2]⟶ ℝ 。对于分割   ，上下和分别是多少？它们之差是多少？

 

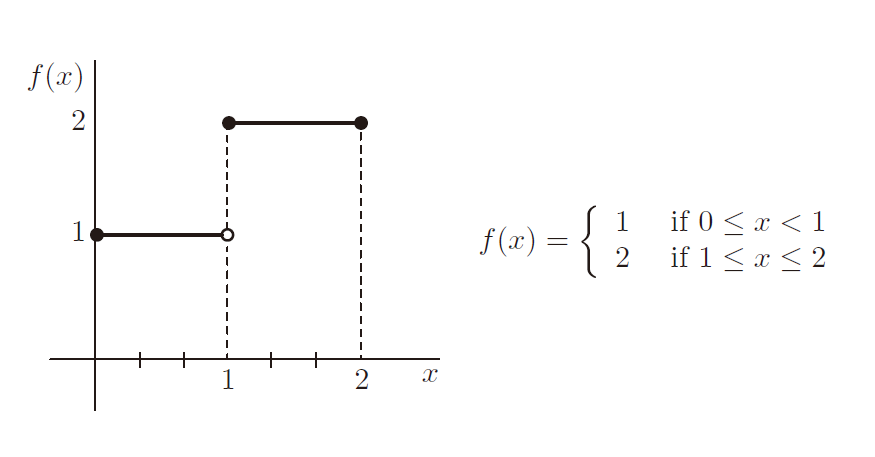
您说差为零吗？那是错的。这显然是错的，所以如果您这么说，那么您的想法就没有什么奇怪的，但您被图表的整体外观误导了。继续之前请再想一想。

         下图是上和的一个可视化表示，如果你说是零，你可以看出为什么是错误的吗？关键是子区间  。点 1 包含于子区间中，且 f (1) = 2 ,因此  且  。

 

我们可以使用不同的分割以使得 U( f；P ) - L( f；P ) 如我们所愿地小吗？答案是肯定的，你可能想思考如何写出一个完整、令人信服的证明(完整并不一定意味着很长)。因此 Riemann 条件得到满足，并且该函数在区间 [0, 2] 上可积。因此函数可以不连续而可积。

         在更高层次上，这里有一些关于数学理论结构需要注意的地方。我将Riemann条件表述为定理，你可能会看到它被证明。然而，该定理具有“当且仅当”结构，这意味着该条件在逻辑上等价于可积性的定义。因此，从技术上讲，我们可以使用Riemann条件作为定义，并将原定义证明为定理。当这种情况发生时，数学家会决定将什么视为基本概念，将什么视为可导出的结果。通常每个人都同意数学家们的这些决定，但你可能会看到某些概念的变体，它们也许出现在不同的教科书中。但这并不意味着不同来源的概念是错误的或过时的——它只是反映了这种逻辑的等价关系。

9.7  涉及可积函数的定理(Theorems involving integrable functions)

         早期关于可积性的许多工作都属于第 3.2 节中讨论的类型。例如，它涉及证明如果 f 和 g 都可以在 [a, b] 上积，那么 f + g 也可以。这类事情的证明往往看起来很长，但它们通常只需要将适当的信息放入下和与上和的定义中，然后将它们相加即可。下面是这样的断言和证明，供阅读练习使用。

断言：若 f 在 [a, b] 上可积，则 3 f在 [a, b] 上可积。

证明：假设 f 在 [a, b] 上可积，并令ε > 0 为任意值。

根据 Riemann 条件，存在 [a, b] 的一个分割P，使得   。

现在， 根据定义，

和

 。

根据上确界(suprema)和下确界(infima)的一般属性，对 ∀j ∈{1，...，n}, 我们有

 

和

 。

因此，U(3 f ；P ) = 3U( f ；P ) 和 L(3 f ；P ) = 3L( f ；P )。

因此，  。

故 3 f  在 [a, b] 上满足 Riemann 条件。

从而 3 f 在[a, b] 上是 Riemann 可积的。

像往常一样，你应该思考这个断言和证明如何推广。如果 3 被 6、-3 或一般常数 c 取代，结果会怎样？为什么关于上确界(suprema)和下确界(infima)的一般性质的结果有效(注：“supremum”是单数，“suprema”是其复数，类似与“maximum”和“maxima”)？我们如何证明，如果 f 和 g 都在 [a, b] 上可积，那么 f + g 也一样(有关启发，请参阅第 5.10 节中收敛序列求和法则的证明)？

         接下来，是一个涉及更多概念的定理。

定理：若 f 在 [a, b] 有界且递增。则f 在 [a, b]上是 Riemann 可积的。

我喜欢这个定理，因为基于Riemann条件的标准证明可以用下图非常优雅地表示出来。论点是，上和与下和之间的差值(灰色框的总面积)与右侧矩形的面积相同。矩形的面积是其宽度的 f (b) – f (a) 倍，因此，只要将宽度缩小到足够小，它就可以小于任何特定的 ε 。因此，Riemann条件得到满足，定理一定正确。

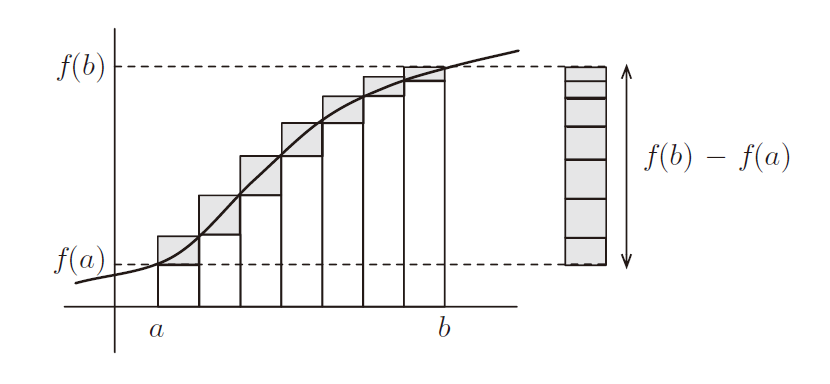
定理：若 f 在 [a, b] 有界且递增。则f 在 [a, b]上是 Riemann 可积的。

证明：令 ε > 0 为任意值。

注意，f (b) – f (a) > 0 ,因为 f 在 [a, b]上是递增的。选择 N ∈ ℕ ，使得  。令  为分割   且对于∀ j∈{ 1 ，...，N } 有  。因为 f 是递增的，因此对于 ∀ j∈{ 1 ，...，N }，我们有

和

 。

因此， 

和 

 。

因此， 

  。

因此，此函数满足 Riemann可积条件，其在 [a, b] 上可积。

         如果 f 在 [a, b] 上递减，这个定理的结论是否仍然成立？如果是这样，证明需要如何改变？这个定理中的函数必须是连续的吗？即使你已经见过很多非连续函数，你的大脑也会默认连续函数，因为它们更熟悉。所以要时不时地提醒自己，要超越显而易见的情况去思考。

9.8  微积分基本定理(The Fundamental Theorem of Calculus)

本章首先非正式地讨论了积分和微分之间的关​​系。这种关系由微积分基本定理(通常缩写为“FTC”)正式描述。如果你学过很多微积分，你可能已经看过 FTC 的证明。然而，微积分课程中的证明往往会做出许多假设。毫不奇怪，分析课程将在定义和早期定理的基础上正确地建立一切。然而，分析课程往往进展得相当快，许多学生在真正理解定理之前就匆匆完成了 FTC 的证明。在这里，我想确保你既理解 FTC 所说的内容，又理解证明它需要什么。

定理(积分基本定理)：假设 f 在 [a, b]上可积，并令   。则

(1) F 在 [a, b]连续；

(2) 若 f 在 [a, b] 上连续，则 F 在 [a, b] 可微且    。

通过检查说明 f 和 F 之间关系的图表，我们可以理解定理前提中的符号：

使用相同的符号，通过思考一般函数 f 和相关 F 的近似值，可以非正式地了解为什么积分和微分是逆运算。从第 8.4 节中，F 在 x 处的导数定义如下。

定义：  (假设这个极限存在)。

然后，考虑这个图和论证。在极限中，当 h ⟶ 0 时就获得了更好的近似，  合理。

 

 

因此，FTC 与积分和微分是逆运算的说法一致。但该定理显然说了比这更精确和更复杂的东西——它关于函数 f 与其积分 F 之间关系的结论取决于 f 的性质，这可能不是你以前考虑过的东西。

    为了准确地理解 FTC 所指，我发现考察具体的例子是有帮助的，例如，考虑由

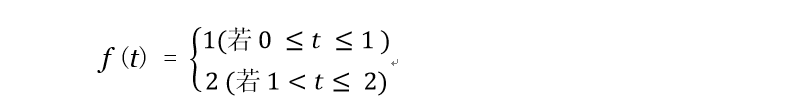
给出的函数 f :[0,2]⟶ ℝ 。

    第 9.6 节确定，尽管此函数在 1 处不连续，但它在 [0, 2] 上可积。因此 FTC 适用。考虑相应积分 F 的图可以阐明 FTC 两个部分的含义。

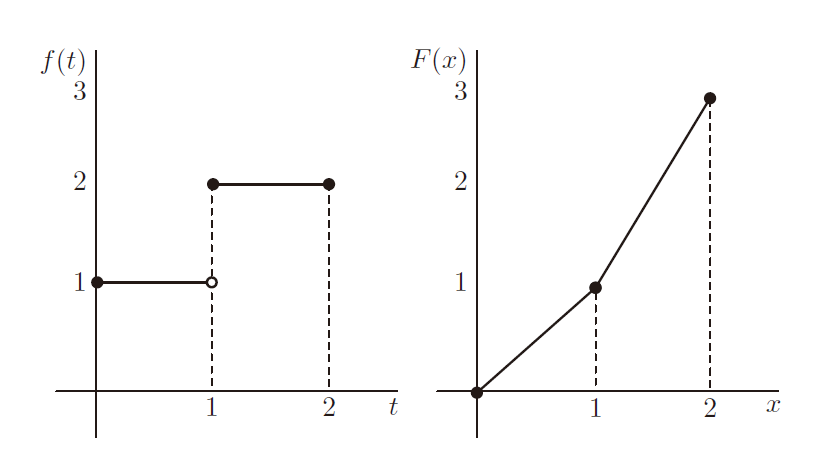
首先，请确保您确信 F 被正确显示。我发现观察以下情况很有帮助：在区间 [0, 1] 上，f 图像下的面积以恒定速率增加，并且积分 F 在 x = 1 时一定达到 1。在区间 [1, 2] 上，f 图形下的面积也以恒定速率增加，但现在该速率加倍，并且积分 F 在 x = 2 时一定达到 3。

    然后考虑 FTC 的第 1 部分，它简单地说，如果 f 是可积的，则 F 是连续的。f 的图在 x = 1 处有一个“跳跃”，但这不会导致 F 中出现相应的跳跃，因为当 x 经过值 1 时，面积不会瞬间跳转到新值。因此，即使 f 不是连续的，F 也是连续的。这应该有助于您理解为什么 FTC 的第 1 部分是合理的。

    FTC 第 2 部分指出，如果 f 是连续的，则 F 是可微的。在我们的例子中，f 在 1 处不连续，F 不可微：F 的图在 x = 1 处有一个“角”。这应该可以解释为什么 FTC 在第 2 部分需要额外的连续性条件：如果 f 不连续，则 F 的梯度/斜率可能会发生急剧变化。总的来说，这是一个微分和积分不是直接逆运算的例子。由于他们早期学习的微分和积分中的大多数函数在任何地方都是连续的，因此这种思想对大多数分析学生来说都是新的。

    证明 FTC 提供了一个机会来整合极限、连续性、可微性和可积性的概念。为了证明第 1 部分，即 F 是连续的，我们需要证明 F 满足连续性的定义(参见第 7.4 和 7.5 节)。这意味着证明对于每一个 c ∈ [a, b]，有以下事实：

    ∀ε > 0 ∃δ > 0使得若 |x – c| < δ 则 |F(x) – F(c)| < ε 。

为了证明第二部分，即 F可微且对于每一个c ∈ [a, b] 都有  ，我们需要证明这些量恰当地符合可微性的定义(见第 8.4 节)。这意味着证明对于每-个 c ∈ (a, b)，有 

 。

进一步利用极限的定义(见第 7.10 节)进行解释，这意味着我们需要证明对于每个 c ∈ (a, b)，有

∀ε > 0 ∃δ > 0使得若 0< |x – c| < δ 则   。

证明最后这个陈述并不像看起来那么难——最后一个表达式可以通过思考 F(x)–F(c) 的含义并使用一些巧妙的代数来简化。还有一些微妙之处需要处理，这些细节可能会在你看到证明之前在你的课程中被考虑。但我们刚刚完成的整理所需内容的工作应该会让你看到的任何证明都更容易理解。

9.9  前瞻(Look ahead)

    与往常一样，分析课程将详细介绍本章的内容，并填补许多空白。如第 9.4 节所述，它可能会使用定义的变体，但使用近似的方法几乎肯定相似。但是，定义的引入可能会有所不同。在这里，我已经抽象地处理了函数和图形，但您的老师可能会鼓励您首先在应用环境中工作，也许根据有关速度随时间变化的方式的信息来近似行进的距离，或者根据有关施加的力在拉伸时变化的方式的信息来近似拉伸弹簧所需的能量。您现在可能想思考这些概念与本章中提出的抽象思想有何关联。

    后面的课程将扩展可积性的概念。有些课程会将其扩展到其他领域。在本章中，所有域都是实数的闭区间子集；多变量微积分课程可能会考虑更多变量函数的积分。例如，函数  以形式为 (x, y) 的点作为输入，并返回实数作为输出，这意味着它的图像可以被认为是三维表面。在这种情况下，积分的域是平面的子集，积分可以被认为是表面下的体积。你认为上和与下和将如何计算？

在另一个方向进行扩展，也可以定义函数 f : ℂ ⟶ ℂ，这为积分开辟了更多的可能性。在复分析课程中，您将学习沿复平面中的曲线进行积分，这自然会引入更多变化，因为有许多不同的曲线连接任何两点。复分析非常优雅，事实证明，对于重要的函数类，无论采用哪种路径，积分都是相同的，这意味着围绕以同一点为起点和终点的曲线的积分一定为零。对于某些函数，只需计算某些点的函数值即可评估积分。这些结果导致了实值函数的应用：一些通常难以计算的实积分可以通过在复平面中围绕半圆进行积分来求得，其直边是实线的一部分，然后取极限使边缘成为实线的整体，并从复积分推断出沿实线的积分。

    最后，如第 9.6 节所述，您可能会了解不同类型的可积性。例如，在测度理论课程中，您可能会了解 Lebesgue 可积性。一些不是Riemann可积的函数是 Lebesgue 可积的，包括第 9.5 节中的这个函数：

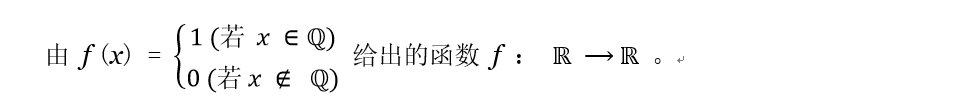
 我们证明了这在任何区间 [a, b] 上都不是Riemann可积的。但它是Lebesgue可积的，并且由于与数轴上有理数的分布有关的原因，其Lebesgue积分为零。这些主题更高级，但我们将在第 10 章对比率数(rational numbers)进行一些初步研究。

内容来源：

<<how to think about analysis>> lara alcock ，Mathematics Education Centre, Loughborough University，Oxford University Press。