羊村懒王

这个屌丝很懒，什么也没留下！

热门标签

对称加密与非对称加密算法

作者：羊村懒王 | 2024-06-10 12:46:11

踩

对称加密

1、密码学概述

密码学是网络安全、信息安全、区块链等产品的基础，常见的对称加密、非对称加密、摘要算法都属于密码学的范畴。

初次接触密码学，可能对一些专有名词不太熟悉，比如密钥、加密算法、密钥交换等。下面通过一个简单的例子介绍下。

H（72）	E（69）	L（76）	L（76）	O（79）
					5（密钥）
M（77）	J（74）	Q（81）	Q（81）	T（84）

上面有一个字符串，HELLO，对应的ASCII码为 72、69、76、76、79。我们对每个字符的ASCII码值加5，得到一串新的ASCII码 77、74、81、81、84。找到对应的字符，就得到了一个新字符串 MJQQT。

通信前，A先把密钥交给B，通信时A用密钥5对HELLO加密(加5)，得到密文MJQQT。然后把密文发送出去，B接受到密文后，使用密钥5对密文MJQQT进行解密(减5)，得到原文HELLO。

这里的HELLO是原文，MJQQT是密文，5是密钥，加和减是加解密算法，A把密钥交给B的过程称为密钥交换或者密钥协商。一般来说，加解密算法都是公开的，但密钥只能通信双方持有，密钥一旦泄露，也就意味着通信不再安全。

这里介绍的是一种最简单的对称加解密，实际使用的加解密算法肯定不会这么简单。下面就主要介绍下目前使用较为广泛的加解密算法。

2、对称加密

对称加密算法又称为传统密码算法，加密密钥和解密密钥是相同的。对称加密算法要求通信双方在开始通信前，要首先商定一个用于加密和解密的密钥。算法的安全性就依赖于这个密钥，如果这个密钥被泄露了，就意味着通信不再安全。

2.1、加密类型

根据加密方式不一样，对称加密算法又分为两种加密类型：流加密和块加密。

2.1.1、流加密

流加密：每次只对明文中的单个位或单个字节进行加密操作。优点是能够实时进行数据传输和解密，缺点是抗攻击能力比较弱。

2.1.2、块加密

块加密(也称为分组加密)：每次对明文中的一组数据进行加密操作。现在使用的分组加密算法典型的分组长度是64位，这个长度大到足以防止破译攻击，而又小到足以方便使用。块加密算法优点是抗攻击能力强，但实时性稍差。

算法模式是块加密法中一系列基本算法步骤的组合。块加密法常用的加密模式：电子编码簿模式(ECB)，加密块链接模式(CBC)，加密反馈模式(CFB)，输出反馈模式(OFB)，计数器模式(CTR)。

电子编码簿模式(ECB)

电子编码簿模式是最简单的操作模式，将输入明文消息分为64位块，然后单独加密每个块，消息中所有块使用相同密钥加密。

加密步骤如下：

从加密步骤我们可以看出，ECB模式中用同一个密钥加密消息的所有块，如果原消息中重复明文块，则加密消息中的相应密文块也会重复。如果输入中一个明文块多次出现，则输出中相应的密文块也会多次出现，从而让攻击者找到漏洞进行破解。

加密块链接模式(CBC)

为了解决ECB模式中相同明文产生相同密文的问题，出现了CBC加密模式。CBC加密模式保证了即使输入中明文块相同，也能得到不同的密文块。CBC加密模式使用了反馈机制。

加密步骤如下：

第一步接收两个输入：明文块1和一个随机文本块IV(Initialization Vector)，称为初始化向量。

初始向量没有什么特别意义，只是使每个消息唯一。初始化向量是随机生成的，可以保证明文块1即使相同也能产生不同密文块1(随机生成的初始化向量相同的概率是很小的)。

加密时第一步使用IV和明文1作异或运算，加密后得到密文1，第二步用密文1和明文2作异或运算，加密后得到密文2，后面依此类推。

初始化向量只在第一个明文块中使用，但所有明文块加密依旧使用相同密钥。

加密反馈模式(CFB)

不是所有应用程序都能处理数据块，面向字符的应用程序也需要安全性。这时要使用流加密法，可以使用加密反馈模式。

加密反馈模式中，数据用更小的单元加密(可以是8位，即一个字符的长度)，这个长度小于定义的块长(通常是64位)。假设我们一次处理j位(j通常取8)。

第一步：

与CBC模式一样，加密反馈模式也使用64位的初始化向量。初始化向量放在移位寄存器中，第一步产生相应的64位初始化向量密文

第二步：

加密初始化向量最左边的j位与明文前j位进行异或运算，产生密文第一部分密文C。

第三步：

初始化向量的位左移j位，使移位寄存器最右边的j位为不可预测的数据，在其中填入C的内容。

第四步：

重复1~3步，直到加密所有明文单元

总体加密过程如下

输出反馈模式(OFB)

输出反馈模式与CFB很相似，唯一差别是，CFB中密文填入加密过程下一阶段，而在OFB中，IV加密过程的输入填入加密过程下一阶段。

计数器模式(CTR)

计数器模式与OFB模式非常类似。它使用序号(称为计数器)作为算法的输入。每个块加密后，要填充到寄存器中，使用下一个寄存器值。通常使用一个常数作为初始计数器的值，并且每次迭代后递增(通常是增加1)。计数器块的大虚哎等于明文块的大小。

加密时，计数器加密后与明文块作XOR运算，得到密文。

2.2、对称加密算法

2.2.1、DES

全称为Data Encryption Standard，即数据加密标准。

DES是一种块加密算法，按64位块长加密数据，即把64位明文作为DES的输入，产生64位密文输出。

DES工作原理

DES使用56位密钥。实际上，最初的密钥为64位，但在DES过程开始之前放弃密钥的每个第八位，从而得到56位密钥，即放弃第8、16、24、32、40、48、56、64位。

2.2.2、3DES

即三重DES，就是三次执行DES，分为两个大类

三个密钥的三重DES

首先用密钥K1加密明文块P，然后用密钥K2加密，最后用密钥K3加密，其中K1，K2，K3各不相同

两个密钥的三重DES

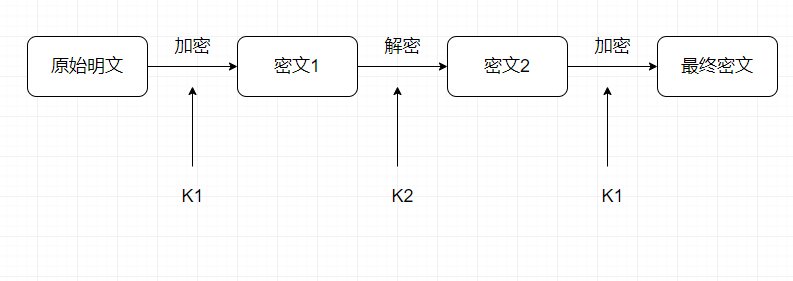
2.2.3、AES

全称为Advanced Encryption Standard，即高级加密标准，这个标准用来替代原先的DES。

1998年6月，Rijndael算法提交给美国国家标准与技术协会(NIST)，作为AES的候选算法之一。最初有15种候选算法。2000年10月，NIST宣布AES最终选择Rijndael。

Rijndael使用的密钥和区块长度可以是32位的整数倍，以128位为下限，256位为上限。AES只选择了区块长度固定为128位，密钥长度为128，192或256位。

2006年，高级加密标准已然成为对称密钥加密中最流行的算法之一。

2.2.4、SM1

SM1 为对称加密。其加密强度与AES相当。该算法不公开，调用该算法时，需要通过加密芯片的接口进行调用。

2.2.5、SM4

SM4由我国国家密码管理局在2012年发布，常用于无线互联网加密等领域。与DES和AES算法类似，SM4算法也是一种分组加密算法。其分组长度为128位，密钥长度也为128位。

2.2.6、RC2

RC2是由RSA安全公司的Ron Rivest在1994年设计的一种块加密算法。输入和输出块大小都是64位。而密钥是可变的，从1字节到128字节。它可作为DES算法的建议替代算法。

RC2属于一种比较老旧的对称式分组算法，已经被时代所抛弃。在当下的绝大多数场景下，都不会推荐使用RC2算法进行加密。

2.2.7、RC4

RC4是由RSA安全公司的Ron Rivest于1987年设计，是一种流加密算法。该算法的速度可以达到DES加密的10倍左右。

RC4加密算法是一种在电子信息领域加密的技术手段，用于无线通信网络。

2.2.8、RC5

RC5是由RSA安全公司的Ron Rivest在1994年设计，是一种块加密算法。块长、轮数、密钥长度都是可变的。块长可取16，32和64位。密钥长度为0~2040位。

RC5算法的特定实例记作R5-w/r/b，其中w为分组长度，r为轮数，b为密钥长度。

RC5-32/16/16 表示RC5的块长为64位(RC5一次加密2字节)，16轮和16字节(128位)密钥。

RC5加密算法在RSA试验室中的表现相当不错，加之其简单、快速的特性，执行所需的内存更少，目前来看算得上是一个比较不错的算法。

3、非对称加密

非对称加密算法是现代密码学取得的最大成就之一，也是密码学近20年来能够快速发展和推广应用的主要原因之一。非对称加密算法中加密密钥和解密密钥不一样，并且解密密钥理论上很难根据加密密钥推算出来。

非对称加密算法的加密密钥是公开的，理论上任何人都可以获得这个公开的加密密钥进行数据加密。但是，使用公开的加密密钥加密的信息只有相应的解密密钥才能解开，而这个解密密钥一般是不公开的。在非对称加密算法中，加密密钥也叫公钥，解密密钥称为私钥。

3.1、非对称加密算法

3.1.1、RSA

RSA是被研究得最广泛的公钥算法，从提出到现在，经历了各种攻击的考验，逐渐为人们接受，普遍认为是目前最优秀的公钥方案之一。

RSA公开密钥密码体制的原理是：根据数论，寻求两个大素数比较简单，而将它们的乘积进行因式分解却极其困难，因此可以将乘积公开作为加密密钥。

RSA算法生成密钥对以及加解密过程：

(1) 选择两个大素数P，Q

设P = 7，Q = 17

(2) 计算N = P x Q

N = 7 x 17 = 119

(3) 选择一个公钥E，使其不是(P - 1)与(Q - 1)的因子

(P - 1) = 6 = 2 x 3

(Q - 1) = 16 = 2 x 2 x 2 x 2

因此我们选的公钥E不能有因子2和3。我们取E = 5

(4) 选择私钥D，满足：(D x E) mod (P - 1) x (Q - 1) = 1

(D x 5) mod 6 x 16 = 1

(D x 5) mod 96 = 1

经计算，取D = 77

(5) 加密时，从明文PT计算密文CT：CT = $PT^{E}$ mod N

假设明文为10

CT = $10^{5}$ mod 119 = 40

(6) 将密文CT发送给接收方

将40发送给接收方

(7) 解密时，从密文CT得到明文PT：PT = $CT^{D}$ mod N

PT = $40^{77}$ mod 119 = 10

从上述例子可以看出，RSA算法本身很简单，关键是选择正确的密钥。

假设B要接收A的加密消息，首先生成公钥E和私钥D，私钥D自己保留，公钥E和数字N发布出去，攻击者拿到公钥E和数字N，似乎可以通过试错法计算出私钥D。这里就到了问题的关键，从上述例子可以看出，攻击者只要从N中分解出P和Q，就可以破解私钥。

有人说因数分解不是很简单嘛，小学生都知道，21可以分解成3乘以7，我口算就能破解密码。但在实际应用中，选取的因数是非常大的，比如2048位的因数，你还能口算分解吗？即使借助性能强大的超级计算机，也需要上百年的时间。

目前1024位的RSA密钥虽然未被破解，但有研究称，在未来十年内，1024位的RSA密钥很可能被破解。因此目前商用RSA密码普遍选用了2048位或者更高的密钥位数。1024位已经被认为不太安全了。

3.1.2、ECC

大多数使用公钥密码学进行加密和数字签名的产品和标准都使用RSA算法。我们知道，为了保证RSA使用的安全性，最近这些年来密钥的位数一直在增加，这对使用RSA的应用是很重的负担，对进行大量安全交易的电子商务更是如此(从上面RSA加解密的例子可以推测，当要使用1024位密钥时，计算量是很大的)。

与RSA相比，ECC可以使用比RSA短得多得密钥得到相同得安全性，因此可以减少处理负荷。另一方面，虽然关于ECC的理论已经很成熟，但ECC的可信度还没有RSA高。

ECC全称为elliptic curve cryptography，即椭圆曲线密码学算法。安全性建立在以下数学困难问题基础之上：

椭圆曲线上的离散对数问题：

已知有限域Fp 椭圆曲线点群Ep (a,b) 及其生成元点P∈Ep (a,b)，P的阶是一个大素数。已知整数

k∈Fp 和点P，求点Q=kP是容易的，但已知点P和Q求整数k则是困难的。

椭圆曲线上的两个点P和Q，k为整数，Q = kP，椭圆曲线加密的数学原理：点P称为基点，k为私钥，Q为公钥。

给定k和P，计算Q很容易。但给定P和Q，求k非常困难。

椭圆曲线方程：y = $x^{3}$ + a $x^{1}$ + b

加解密过程：

(1) 用户选定一条椭圆曲线Ep(a, b)，并取椭圆曲线上一点作为基点P

(2) 用户A选择大数k作为私钥，并生成公钥Q = kP

(3) 用户A将Ep(a, b)，公钥Q和基点P传给B用户

(4) 用户B接受到信息后，将待传输的明文编码到Ep(a,b)上的一点M，并产生一个随机整数r。

(5) 用户B计算点C1 = M + rQ，C2 = rP

(6) 用户B将C1和C2传给A

(7) 用户A接收到信息后，计算C1 - kC2，就可以得到点M(C1 - kC2 = M + rQ - krP = M + r(Q - kP) = M)。

(8) 再对M进行解码就可以得到明文。

假设在加密过程中，有一个第三者H，H只能知道椭圆曲线 Ep(a,b)、公钥Q、基点P、密文点C(C1, C2)，而通过公钥Q、基点P求私钥k或者通过密文点C(C1, C2)、基点P求随机数r都是非常困难的，因此得以保证数据传输的安全。

密码学中，描述一条Fp上的椭圆曲线，常用到六个参量：T=(p，a，b，n，x，y)。（p 、a 、b）用来确定一条椭圆曲线，p为素数域内点的个数，a和b是其内的两个大数；x，y为G基点的坐标，也是两个大数；n为点G基点的阶；以上六个量就可以描述一条椭圆曲线。

比特币使用的加密算法就是ECC，选取的曲线名称是 NID_secp256k1

3.1.3、SM2

SM2算法是我国自主知识产权的商业密码算法，是ECC的一种。

ECC是基于椭圆曲线方程 y = $x^{3}$ + a $x^{1}$ + b，SM通过指定系数a，b确定了唯一的一条曲线。简单理解就是ECC选取的椭圆曲线可以有很多个，而SM2只是选取了唯一的一条椭圆曲线。

SM2椭圆曲线公钥密码算法推荐曲线参数

推荐使用素数域256位椭圆曲线。

椭圆曲线方程：y = $x^{3}$ + a $x^{1}$ + b

曲线参数：

p=FFFFFFFE FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF 00000000 FFFFFFFF FFFFFFFF

a=FFFFFFFE FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF 00000000 FFFFFFFF FFFFFFFC

b=28E9FA9E 9D9F5E34 4D5A9E4B CF6509A7 F39789F5 15AB8F92 DDBCBD41 4D940E93

n=FFFFFFFE FFFFFFFF FFFFFFFF FFFFFFFF 7203DF6B 21C6052B 53BBF409 39D54123

Gx=32C4AE2C 1F198119 5F990446 6A39C994 8FE30BBF F2660BE1 715A4589 334C74C7

Gy=BC3736A2 F4F6779C 59BDCEE3 6B692153 D0A9877C C62A4740 02DF32E5 2139F0A0

国家密码管理局已经发布了《SM2椭圆曲线公钥密码算法》公告，对SM2算法有非常详细的说明，感兴趣的读者可以自行去查阅。
国家密码管理局关于发布《SM2椭圆曲线公钥密码算法》公告（国密局公告第21号）_国家密码管理局 (oscca.gov.cn)https://oscca.gov.cn/sca/xxgk/2010-12/17/content_1002386.shtml

3.1.4、ElGamal

ElGamal加密算法是一种基于离散对数难题的非对称加密算法，由Taher ElGamal在1985年提出。

离散对数问题的难解性主要基于费马小定理的推理。

费马小定理指出，如果p是一个素数，a是与p互质的整数，那么a^(p-1) ≡ 1 (mod p)。根据费马小定理，我们可以得到一个等式：a^x ≡ a^(x mod (p-1)) (mod p)。因此，如果我们能够找到一个整数y，使得b ≡ a^y (mod p)，那么我们可以将离散对数问题转化为求解指数问题。

但是当p是一个很大的素数时，求解整数y就变得异常困难。这就是离散对数问题的难解性所在。

ElGamal算法加解密过程

(1) 在生成密钥时，首先随机选择一个大素数p，要求p-1有大素数因子。再选择一个模p的本原元g，将p和g公开

取 p = 11，g = 2

(2) 随机选择一个整数 pri 作为私钥，要求 2 ≤ pri ≤ p-2

取 pri = 3

(3) 计算公钥pub = g ^ pri mod p

pub = $2^{3}$ % 11 = 8

(4) 随机选取一个整数 k，要求 2 ≤ k ≤ p-2

取 k = 4

(5) 加密求密文c1, c1 = g ^ k mod p

c1 = $2^{4}$ % 11 = 5

(6) 加密求密文c2，c2 = m * pub ^ k mod p，这里m是明文(m必须小于p)，我们取m=7

c2 = (7 * $8^{4}$ ) % 11 = 6

(7) 得到密文(c1, c2), 将密文发送给解密方

(8) 解密方解密得到原文m'， m' = c2 / c1 ^ pri mod p

m' = c2 / c1 ^ pri mod p = c2 * inv(c1) ^ pri mod p = c2 * (c1 ^ (p - 2) mod p) ^ pri mod p

m' = (6 * (5 ^ 9 % 11) ^ 3) % 11 = (6 * 9 ^ 3) % 11 = 7

这一步转换涉及到数论中逆元的概念

(c2 / c1) % p 需要转换为c2 * inv(c1) % p, inv(c1) 称为 c1 对 p 取余意义下的逆元

根据费马小定理求逆元：inv(c1) = c1 ^ (p - 2) mod p

C++代码实现


#include<stdio.h>
#include<stdlib.h>
#include<math.h>
 
void elgamalEncrypt(int m, int pub, int p, int g, int *c1, int *c2){
        int k = 4;
 
        // c1 = g ^ k mod p
        *c1 = (int)pow(g, k) % p;
 
        // c2 = m * pub ^ k mod p
        *c2 = (int)(m * pow(pub, k)) % p;
}
 
int elgamalDecrypt(int c1, int c2, int pri, int p){
        int x = (int)pow(c1, p - 2) % p;
        int m = (c2 * ((int)pow(x, pri) % p)) % p;
        return m;
}
 
 
int main(){
        // 大素数p
        int p = 11;
 
        // p的本原元 g
        int g = 2;
 
        // 私钥 D
        // 2 <= D <= p - 2
        int pri = 3;
 
        // 求公钥
        int pub = (int)pow(g, pri) % p;
        printf("private key : %d\n",pub);
 
        // 明文
        int m = 7;
 
        // 求密文(c1, c2)
        int c1 = 0, c2 = 0;
        elgamalEncrypt(m, pub, p, g, &c1, &c2);
        printf("encrypt msg : c1=%d, c2=%d\n",c1, c2);
 
        // 解密明文 m_
        int m_ = elgamalDecrypt(c1, c2, pri, p);
        printf("decrypt msg : %d\n", m_);
 
        return 0;
}

3.1.5、Diffie-Hellman

Diffie-Hellman 密钥交换协议/算法由 Whitefield Diffie 与 Martin Hellman 在1976年提出。Diffie-Hellman算法本身是非对称加密的一种, 但这个算法只能用于密钥交换，不能用于加解密。

Diffie-Hellman 算法的安全性在于，在有限域中的离散对数计算难度比同一个域中的指数计算难得多

密钥交换过程

(1) Alice与Bob确定两个大素数n和g，可以不保密

取 n = 11， g = 7

(2) Alice选择另一个大随机数x，并计算 A = g ^ x mod n

取 x = 3，A = 7 ^ 3 mod 11 = 2

(3) Alice将A发给Bob

(4) Bob选择另一个大随机数y，并计算 B = g ^ y mod n

取 y = 6, B = 7 ^ 6 mod 11 = 4

(5) Bob将B发给Alice

(6) Alice计算共享密钥K1

K1 = B ^ x mod n = 4 ^ 3 mod 11 = 9

(7) Bob计算共享密钥K2

K2 = A ^ y mod n = 2 ^ 6 mod 11 = 9

通过密钥交换过程可以看出来，最终计算的K1和K2是相等的，后续就可以用这个共享密钥进行加解密了。

x可以看作Alice的私钥，A为公钥。y可以看作Bob的私钥，B为公钥。Alice和Bob的公钥虽然在交换过程中可能被截获，但由于攻击者没有Alice和Bob的私钥，也就无法计算出这个共享密钥，因此该共享密钥就是安全的。

那么攻击者能不能推断出Alice的私钥x的值，从而求出共享密钥呢？首先看一下，n和g是公开，Alice的公钥A也是公开的，能通过A = g ^ x mod n 求出x的值吗？显然是不行的，因为A是通过模运算求出来的，反向是无法推断出x的值的。

Diffie-Hellman算法本身是安全的，但是它存在一个被称为"中间人攻击"的漏洞。攻击者可以截获Alice和Bob之间交换的公钥，然后冒充Alice或Bob与其他人进行密钥交换。

攻击过程

(1) 攻击者截获Alice的公钥A，然后自己生成一个私钥 x', 并计算出公钥 A'

取 x' = 4, A' = 7 ^ 4 mod 11 = 3

(2) 攻击者将 A' 发给Bob

(3) 按照上面步骤，Bob计算B的方法不变

B = g ^ y mod n = 7 ^ 6 mod 11 = 4

(4) Bob将B发给A，被攻击者截获

(5) 攻击者计算 K1' = B ^ x' mod n = 4 ^ 4 mod 11 = 3

(6) Bob计算 K2' = A' ^ y mod n = 3 ^ 6 mod 11 = 3

可以看到攻击者冒充Alice, 和Bob协商了一个共享密钥，后续攻击者可以使用这个共享密钥和Bob通信。

为了防止中间人攻击，可以使用数字签名等其他加密技术来验证通信方的身份。

4、对称加密与非对称加密技术比较

对称加密

优点：加密速度快

缺点：密钥管理分配困难，安全性较低

非对称加密

优点：安全性较高

缺点：加密速度慢

对称加密技术加密和解密使用的都是同一个密钥，因此密钥的管理非常困难，在分发密钥的过程中，如果密钥被截获，那后面的通信就是不安全的。而非对称加密技术就很好的解决了这一问题，非对称加密技术使用公钥加密，私钥加密。通信前把公钥发布出去，私钥只有自己保留，即便你的公钥被攻击者拿到，没有私钥，就无法进行解密。

那有了非对称加密技术，对称加密是不是就被淘汰了？当然不是，从非对称加密算法的原理可以看出，加密过程涉及到大量的计算，因此不适合对于大量数据进行加密。

一般使用对称加密算法加密一些安全性要求较低，数据量较大的数据，比如文件的加密，聊天信息的加密。使用非对称加密算法加密安全性要求较高，数据量较小的数据，比如个人密码、个人信息等。当然也可以将两者结合使用。

5、摘要(哈希)算法

严格意义来说，摘要或者哈希算法并不属于加解密算法，因为哈希算法是单向加密的，也就是说只能加密，不能解密，但都同属于密码学的范畴。常见的哈希算法有MD5、SHA-1、SM3等。

当然，摘要算法的作用也不是为了进行数据的加解密，摘要算法主要用于检验数据完整性或者说校验数据是否被篡改。比如我们对文件做一个摘要，只要有人修改过文件内容，那么摘要值就和原摘要值不一样了，我们可以据此判断文件是否被篡改。

具体可参考我的另一篇文章中对摘要算法的介绍。

消息摘要算法与消息认证码简介_消息摘要和消息认证码-CSDN博客

6、实践

说了这么多理论，接下来可以使用OpenSSL的命令行工具，进行实际的加解密体验下。

OpenSSL安装和命令行工具介绍_openssl工具_大草原的小灰灰的博客-CSDN博客

参考资料

《密码编码学与网络安全》 -[美] William Stallings 著电子工业出版社

《密码学与网络安全》-Atul Kahate著清华大学出版社

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/羊村懒王/article/detail/698855