数字图像处理》第6讲——频域图像增强_为什么要在频率域研究图像增强?

虽然写这个博客主要目的是为了给我自己做一个思路记忆录，但是如果你恰好点了进来，那么先对你说一声欢迎。我并不是什么大触，只是一个菜菜的学生，如果您发现了什么错误或者您对于某些地方有更好的意见，非常欢迎您的斧正！

目录

①频域是什么？

②为什么要在频率域研究图像增强？

③傅里叶变换的频率分量与图像空间特征之间的联系

④频域的滤波步骤

⑤一些基本的滤波器

1、陷波滤波器

2、低通滤波器

3、高通滤波器

⑥空域滤波与频域滤波的关系

⑦频域平滑滤波器

1、理想低通滤波器

2、巴特沃思低通滤波器

3、高斯低通滤波器

4、应用实例

⑧频域锐化滤波器

1、理想高通滤波器

2、巴特沃思高通滤波器

3、高通滤波器

4、应用举例

⑨同态滤波

---

①频域是什么？

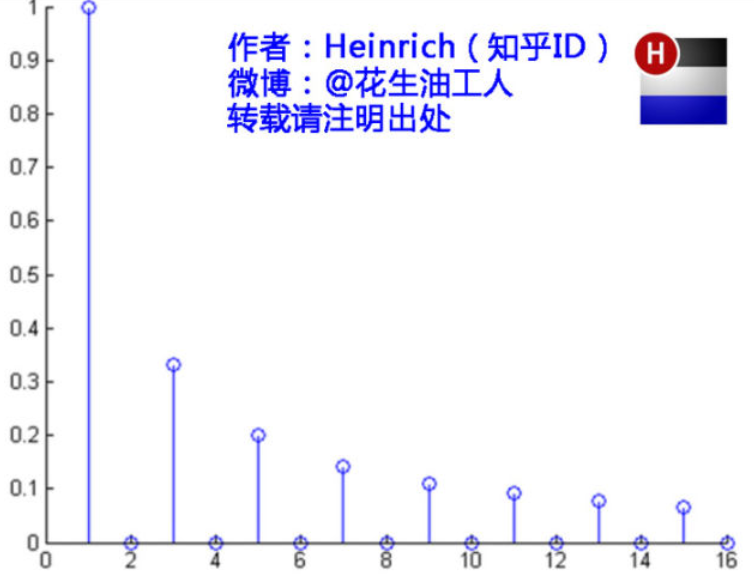
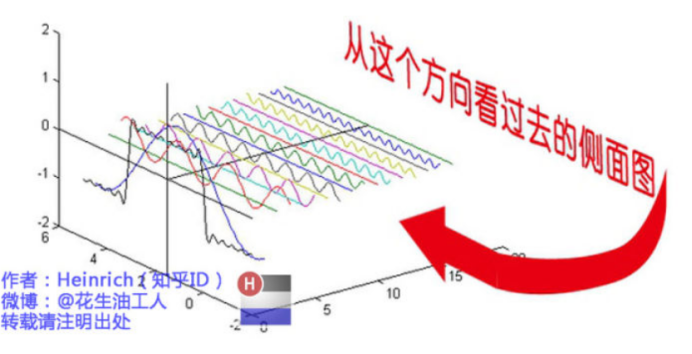
首先回想一下，什么是频域。我在写上一篇文章的时候，曾经搜到了一篇非常好的文章，是讲解“傅里叶级数”的，里面就有关于频域的十分具象的描述，我在这里放一下链接：

傅里叶分析之掐死教程（完整版）

https://zhuanlan.zhihu.com/p/19763358

我接下来回答“频率是什么”这个问题的图就是来源自这篇文章。

如果你看了这三张图还不懂频域是个什么东西，那么你就点那篇文章去好好看一下，那篇文章确实写的很没节操。如果你认真仔细看了那篇文章还是不懂，那么你就去掐死那个作者，毕竟这是他自己立下的flag。、

②为什么要在频率域研究图像增强？

✔可以利用频率成分和图像外表之间的对应关系。一些在空间域表述困难的增强任务，在频率域中变得非常普通。

✔滤波在频率域更为直观，它可以解释空间域滤波的某些性质

✔可以在频率域指定滤波器，做反变换，然后在空间域使用结果滤波器作为空间域滤波器的指导。

✔一旦通过频率域试验选择了空间滤波，通常实施都在空间域进行。

 

③傅里叶变换的频率分量与图像空间特征之间的联系

✔变化最慢的频率成分（u=v=0）对应一幅图像的平均灰度级。

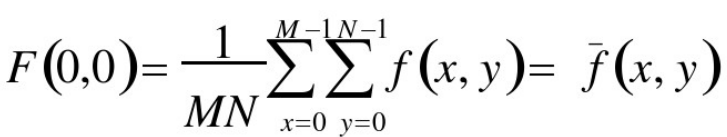
✔当从变换的原点移开时，低频对应着图像的慢变化分量，如图像的平滑部分。

✔进一步离开原点时，较高的频率对应图像中变化越来越快的灰度级，如边缘或噪声等尖锐部分。

 

④频域的滤波步骤

思想：通过滤波器函数以某种方式来修改图像变换，然后通过取结果的反变换来获得处理后的输出图像。（通俗地说，我想用滤波器加工一幅图像，比如瞎扯地说，我的滤波器把图像倒过来比较容易加工，那么我的图像就是输入->倒过来->加工->倒回去->输出这样一个过程）

1、用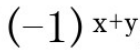乘以输入图像来进行中心位移

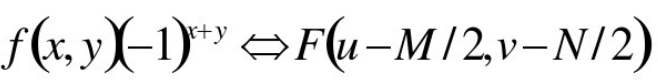
2、计算图像的DFT，即F(u,v)——傅里叶变换

3、用滤波器函数H(u,v)乘以F(u,v)

4、计算F(u,v)H(u,v)的反DFT

5、取(4)步骤结果中的实部

6、用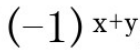乘以(5)中的结果，取消输入图像的乘数。

其中H(u,v)称为滤波器。

 

⑤一些基本的滤波器

1、陷波滤波器

✔设置F(0,0)=0（结果图像的平均值为0，为什么是这个式子，在③的第一条提到过），而保留其它傅里叶变换的频率成分不变。

✔除了原点处有点凹陷外，其它均是常量函数。

✔由于图像平均值为0而产生整体平均灰度级的降低。

✔用于识别由特定的、局部化频域成分引起的空间图像效果。

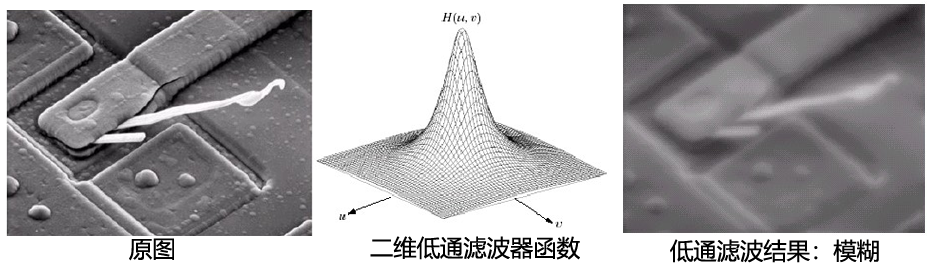
2、低通滤波器

使低频通过而使高频衰减的滤波器（大概就是模糊）

✔被低通滤波的图像比原始图像少尖锐的细节部分而突出平滑过渡部分。

✔对比空间域滤波的平滑锤炼，如均值滤波器。

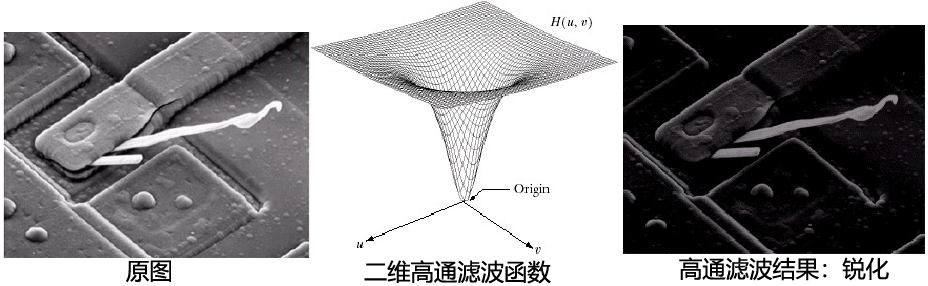
3、高通滤波器

使高频通过而使低频衰减的滤波器（大概就是锐化）

✔被高通滤波的图像比原始图像少灰度级的平滑过渡而突出边缘等细节部分

✔对比空间域的梯度算子、拉普拉斯算子

⑥空域滤波与频域滤波的关系

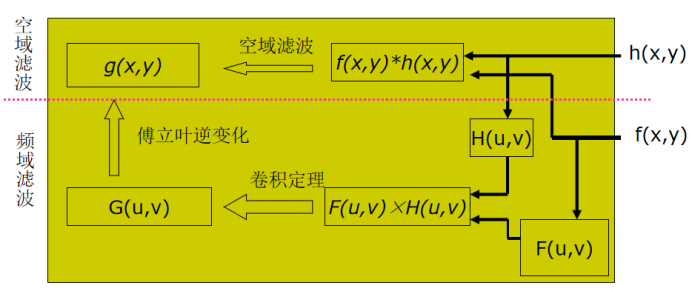
⑦频域平滑滤波器

1、理想低通滤波器

✔截断傅里叶变换中所有高频成分，这些高频成分处于指定距离之外。为截止频率。

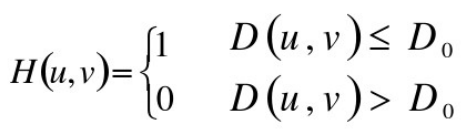
✔频率矩形的中心在(u,v)=(M/2,N/2)，从点(u,v)到中心（原点）的距离如下

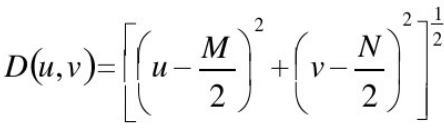
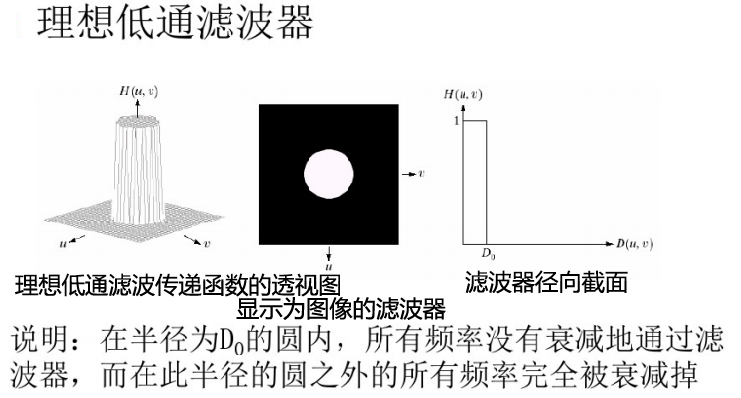
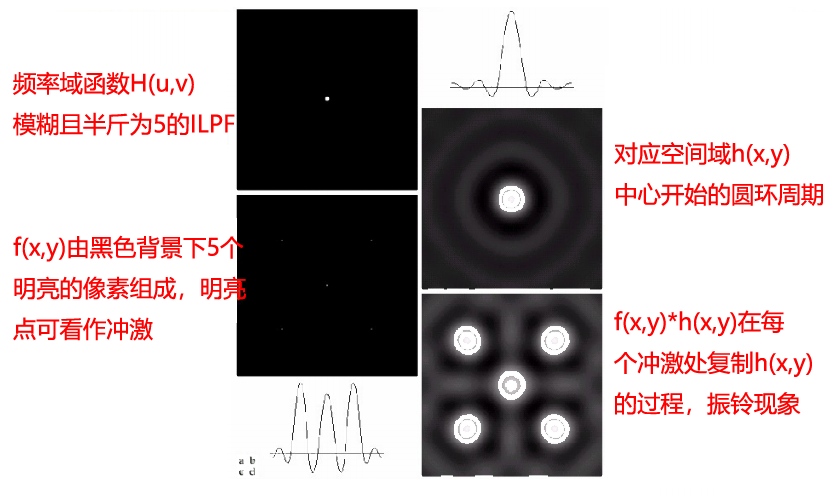
理想低通滤波器（ILPF）的特点：

✔物理上不可实现

✔有振铃效应

✔滤除高频部分使图像变模糊

2、巴特沃思低通滤波器

✔n阶巴特沃思低通滤波器(BLPF)定义如下：

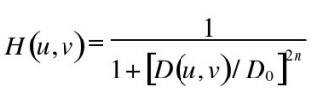
✔为截至频率距原点的距离，D(u,v)是点(u,v)距原点的距离。

✔不同于ILPF，BLPF变换函数在通带与被滤除的频率之间没有明显的截断。

✔当D(u,v)=时，H(u,v)=0.5（最大值是1，当D(u,v)=0）

✔应用：可用于平滑处理，如图像由于量化不足产生虚假轮廓时，常可用低通滤波进行平滑以改进图像质量。通常，BLPF的平滑效果好于ILPF（振铃现象）。

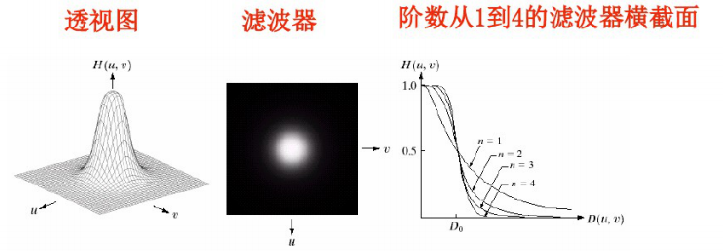
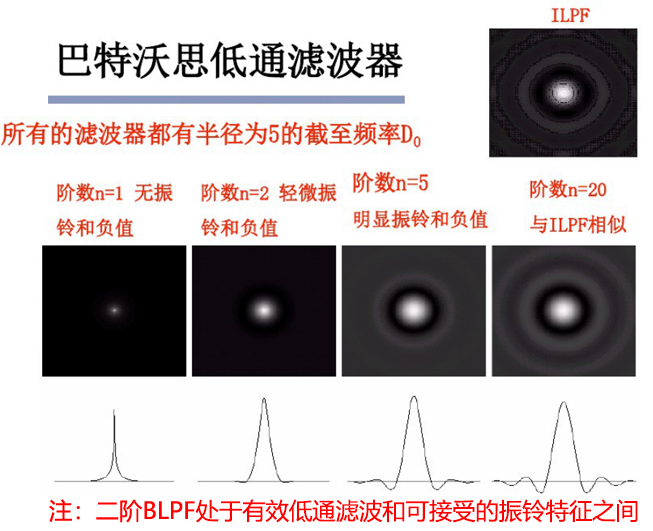
巴特沃思滤波器（BLPF）的特点：

✔一阶巴特沃思滤波器没有振铃效应，二阶振铃效应很小，随着阶数的增加，振铃效应加重

✔阶数n趋于无穷时，巴特沃思滤波器称为理想滤波器

✔二阶巴特沃思滤波器是有效的低通滤波和可接受的振铃效应之间的折中

3、高斯低通滤波器

✔二维高斯低通滤波器（GLPF）定义如下：

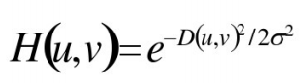
✔D(u,v)是点(u,v)距原点的距离，使σ=

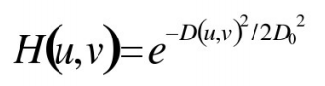
✔当D(u,v)=时，滤波器下降到它最大值的0.607处

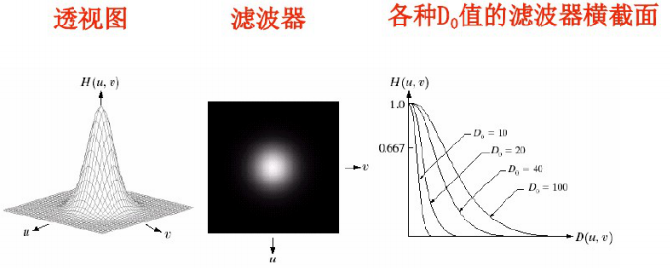
高斯低通滤波器（GLPF）的特点：

✔GLPF不能达到有相同截止频率的二阶BLPF的平滑效果

✔GLPF没有振铃

✔如果需要严格控制低频和高频之间截止频率的过度，选用BLPF，代价是可能产生振铃。

 

4、应用实例

低通滤波器的应用实例：模糊，平滑等。

✔字符识别：通过模糊图像，桥接断裂字符的裂缝。

✔印刷和出版业：从一幅尖锐的原始图像产生平滑、柔和的外观，如人脸，减少皮肤细纹的锐化程度和小斑点。

✔处理卫星和航空图像：尽可能模糊细节，而保留大的可识别特征。低通滤波通过消除不重要的特征来简化感兴趣特征的分析。

 

⑧频域锐化滤波器

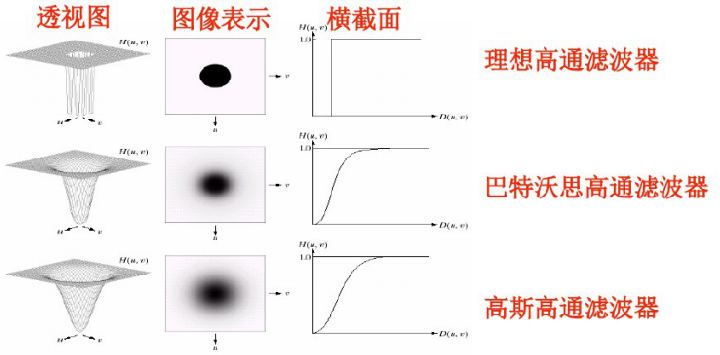
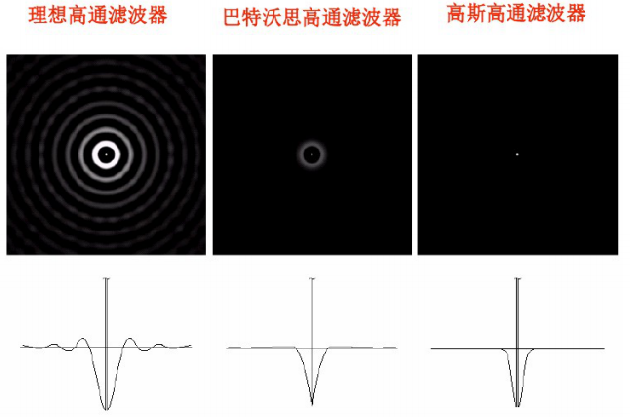
1、理想高通滤波器

✔截断傅里叶变换中所有低频成分，这些低频成分处于指定距离之内。为截止频率。

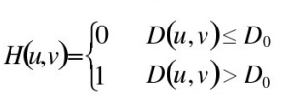
✔频率矩形的中心在(u,v)=(M/2,N/2)，从点(u,v)到中心（原点）的距离如下

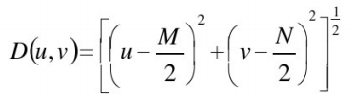
2、巴特沃思高通滤波器

✔n阶且截至频率距原点的距离为的巴特沃思高通滤波器(BHPF)定义如下：

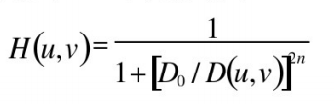
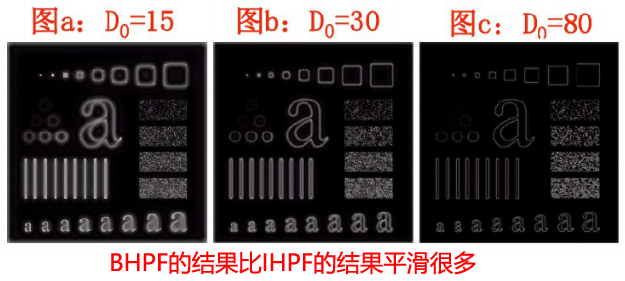
3、高通滤波器

✔截至频率距原点为的高斯高通滤波器(GHPF)定义：

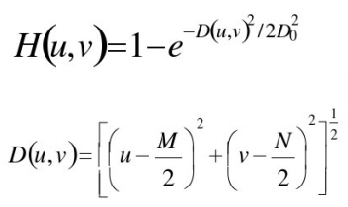
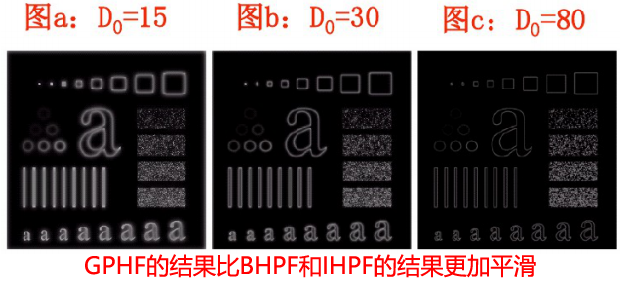
*频域的拉普拉斯算子

*钝化模板、高频提升滤波和高频加强滤波

4、应用举例

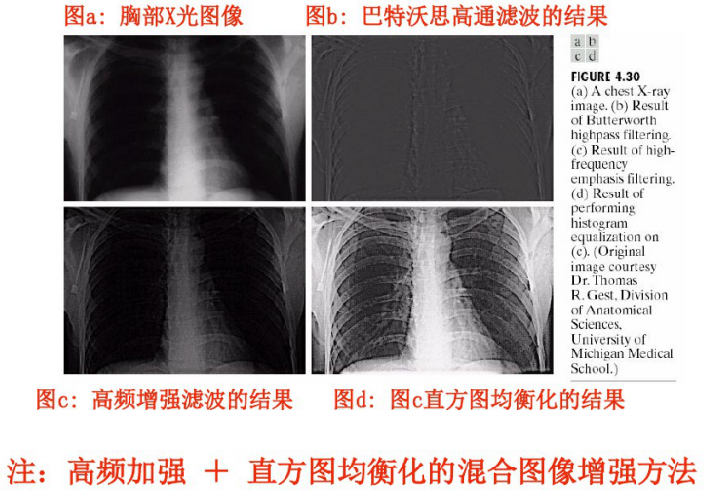
⑨同态滤波

✔把图像的灰度函数f (x, y)看成是由入射光分量和反射光分量两部分组成的

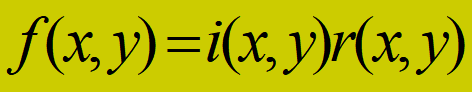
✔  i(x, y)：入射光

     r(x, y)：反射光－－取决于物体的特性

           物体的亮度特征主要取决于反射光

 

✔入射光较均匀，随空间位置变化较小～～占据低频段；反射光由于物体性质和结构特点不同而反射强弱很不相同的光，随空间位置变化较剧烈

✔  入射光～～占据低频段

     反射光～～占据高频段比较宽的范围

总结以上过程，同态滤波可以用下图来表示其计算过程：