迪杰斯特拉(Dijkstra)算法_dijkstra算法

一 算法介绍

迪杰斯特拉算法是由荷兰计算机科学家在1956年发现的算法，此算法使用类似广度优先搜索的方法解决了带权图的单源最短路径问题。它是一个贪心算法。

二 核心思想

1. 选定一个点，这个点满足两个条件：1.未被选过，2.距离最短

2. 对于这个点的所有邻近点去尝试松弛

三 算法步骤 

首先，可以设置两个集合分别是A和B，A用来存放已经求出最短路径的点，B用来存放还未计算出最短路径的点，接下来就可以开始做题啦！！！

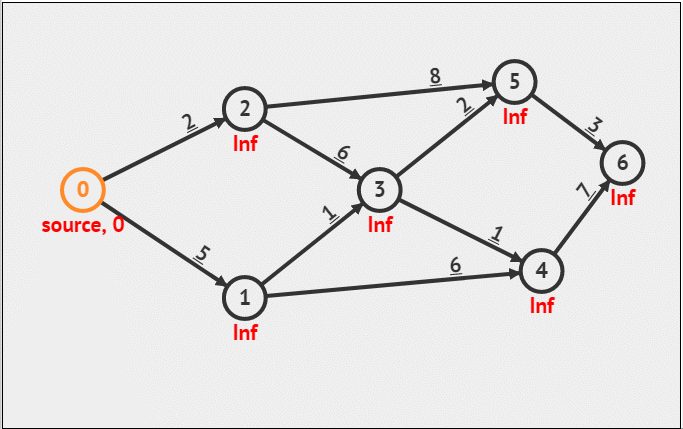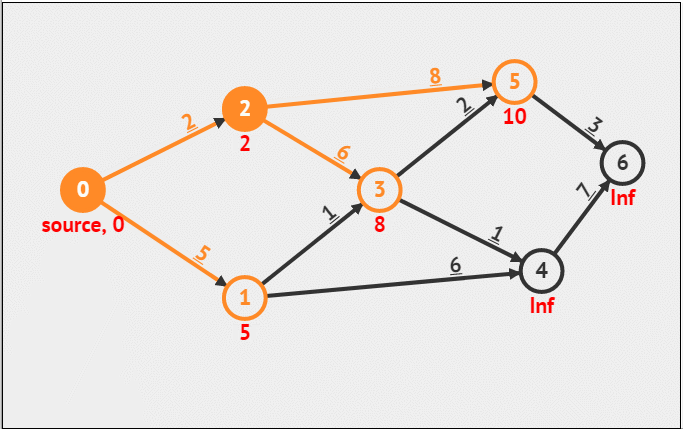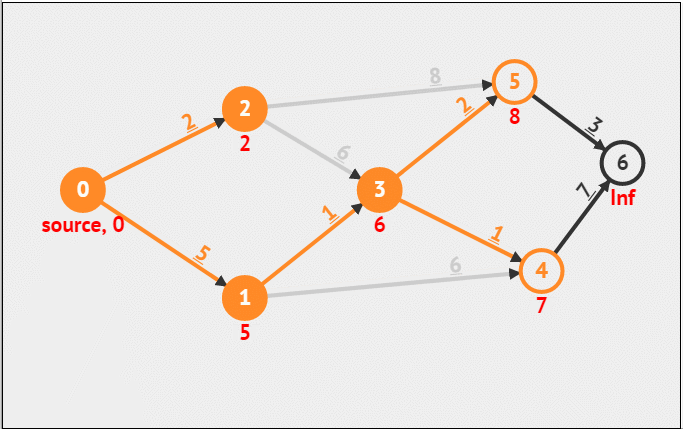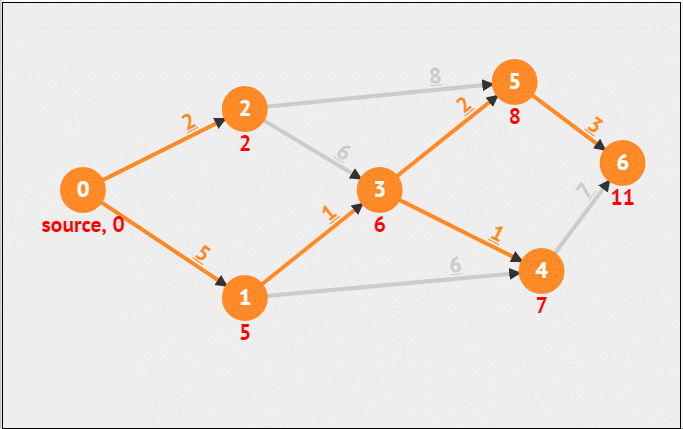
我们从图中任选一点来解题，假设我们将源点source选择在” 0 "这个点。一开始所有点到达源点0的距离我们假设为∞，代表不可达。源点0到自己本身的距离为0，初始化如下：此时A集合为：{0}，B集合为：{1，2，3，4，5，6}

第一步：从0点开始，更新和0邻接的所有点的距离，此时，因为与0邻接的有1和2，并且到这两个点的距离，小于原来的∞距离，所以要将这两个点到0的距离都进行更新如下图，

第二步：从B集合里面选择一个点加入A集合，这个点要满足距离0点的距离最短，因此我们选择2这个点添加到集合A，此时集合A变为：{0,2}，集合B变为：{1，3，4，5，6}，如下图

第三步：选择刚刚加入的这个2点，更新所有与2点邻接的点，因为与2邻接的点有3和5，并且这两个点到0点的距离小于原来它们到0点的距离∞

第四步：从B集合里面选择1这点加入到集合A中，因为1这个点在B集合中距离0最近，如下图，此时A集合变成：{0,1,2}，B集合变成：{3,4,5,6}

第五步：选择刚刚加入的1这个点，更新1所有的邻接点，它的邻接点有3和4，因为此刻从0到3的距离为6，小于原来0到3的距离8，因此这个时候到6的距离更新为6(5+1)，此时0到4的距离被更新为11

第六步：从B集合中选择一个距离0点最小距离的点，加入集合A，此时可以选择3这个点，因为3这个点在B集合里面距离0点最近，此时集合A变为：{0,1,2,3}，集合B变为：{4,5,6}

第七步：从刚刚选择的这个3点出发，更新3所有的邻接点，3的邻接点有4和5，原来4到0的距离为11，3加进来之后，4到0的距离为7，小于原来的11，所以要更新，原来5到0的距离为10，3加进来之后，5到0的距离为8，所以也要更新

第八步：从B集合中选择一个距离0点最小距离的点，因此我们选择4点，因为此时4这个点距离0点最近，为7，于是集合A变成：{0,1,2,3,4}，集合B变成：{5,6}

第九步：从刚刚选择的点4出发，更新它的所有邻接点，4的邻接点有6，原来6到0的距离为∞，此时4加进来之后6到0的距离变为14，它小于∞，因此要更新6到0的距离，更新为11

第十步：从集合B中选择一个距离0点最短距离的点，加入集合，此时我们可以选择5这个点，因为这个时候它在B集合中是距离0点最近的点，于是集合A变为：{0,1,2,3,4,5}，集合B变为{6}

第11步：从刚刚选择的这个点出发，也就是从点5出发，更新它所有的邻接点，此时5的邻接点为6，原来0到6的距离为14，此时点5加进来之后，0到6的距离变为了11，因此需要更新0到6的距离

第12步：因为B集合只剩下一个点，为点6，直接将其加入A集合即可，此时A集合变为:{0,1,2,3,4,5,6}，B集合变为:{ }，至此，从0点到其它所有点的最短路径已经算出来了，为下图

四 注意事项

1.不能处理带有负权边的图(可能得不到最优解，认为是无法处理负权图)，只能处理非负权图。

          为什么? ，以此图为例，按照Dijkstra的思想，首先0点加入集合，然后1点加入集合，然后3点加入集合，然后2加入集合，此时0->2更新为99-300，但是此刻已经无法更新0->3（原来的值为2）了。

              

2.只能解决单源最短路径问题

五  核心代码 

                                                                                   

以此图为例，写一段测试代码。使用邻接矩阵来存储图结构，100代表两点之间没有通路，看成无穷，你也可以使用比图中距离大的任何一个数。如下图

                                                                              

使用的数据结构有：vector，在这里，我们将最核心的代码封装成一个函数，我们最终的目的是求出某一个源点到其它点的最短距离，那么返回值可以是一个vector。并并且我们需要两个参数，分别代表图结构和源点，函数定义如下：

const int inf = 500;  //可以给别的值，只要大于图中任何一边的距离即可
vector<int> dijkstra(vector<vector<int> > G,int source)
{
    int n = G.size(); //n代表图的顶点个数
    vector<int> dis(n,inf); //dis代表源点到其它点的最短距离，inf代表无穷，初始化vector
    vector<int> vis(n,false); //vis代表某个顶点是否被访问过，初始化所有的顶点为false
    //源点到源点的距离为0
    dis[source]=0;
    
    /*
        根据前面咱们的分析可以知道，要不断寻找没有被访问过且距离源点最近的点，有n个顶点，
        就要寻找n-1次，找到点之后，对其邻接点进行松弛，为什么只要寻找n-1个点呢？因为当
        剩下一个点的时候，这个点已经没有需要松弛的邻接点了。此时从源点到这个点的距离就是最短距离了。
    */
    //可以使用一个for循环，循环n-1次，来寻找n-1个点
    for(int i=0; i<n-1; i++)
    {
        int node = -1;  //进入循环之后，假设一开始不知道哪个是没有被访问过且距离源点最短的点
        for(int j=0;j<n;j++)  //使用这个循环开始寻找没有被访问过且距离源点最短距离的点
        {
            if(!vis[j] && (node == -1 || dis[j]<dis[node]))
            {
                node = j;  //把当前距离源点最短距离的点给node
            }
        }
        //对这个距离源点最短距离的点的所有邻接点进行松弛
        for(int j=0; j<n; j++)
        {
            dis[j]=min(dis[j],dis[node]+G[node][j]);
            /*
                这边要特别注意：对于不是node的邻接点并不会影响它原来的距离，以2点为例
                对于邻接的已经访问过的点也不会产生影响，以3点为例
            */
        }
        //标记为已访问过
        vis[true];
    }
    return dis;
}

 

六 心得体会

有时候一开始不会，代码也看不懂，觉得不想照打一遍，觉得那是浪费时间，其实不然，如果不会，先按照别人的思路打一遍，然后自己带数据进去走一遍代码，带着数据多走几遍，很快就能明白。各位小伙伴们，欢迎大家来进行讨论！！！