【滤波专题-第9篇】类EMD分解算法联合小波阈值降噪及MATLAB代码实现（以ICEEMDAN-样本熵-小波阈值降噪方法为例）

今天这篇介绍的算法，由于其高度的灵活性、使用方法的丰富性以及不错的效果，堪称水论文神器。对于需要使用滤波算法的同学们，这篇文章不可错过~

本篇会提及很多前置概念，比如ICEEMDAN等模态分解算法、熵特征提取、小波阈值滤波等等，这些概念在本专栏之前的系列文章中都有着详细的讲解，本篇在讲到这些概念时将不再详细展开，需要相关信息的同学可以点击我在正文中插入的文字超链接，或者在文末的拓展阅读中查找。

一、算法概述

常写和不常写论文的同学们应该都知道，论文撰写中必不可少的就是创新点。创新点又有纵向深挖和横向拓展之分，纵向深挖往往需要对原理的透彻理解和深入思考，能在此方向突破自然是大大的不俗；但是对于时间紧任务重的同学来说，做算法在横向的拓展应用可能是更便捷有效的方式。也正是因此，很多论文使用的方法名字变得越来越长，一口气读下来颇有龙妈头衔的即视感。

安达尔人、洛伊拿人和先民的女王、七国女王/统治者、全境守护者、大草海的卡丽熙、镣铐/锁链破除者、风暴降生、弥林女王、龙石岛公主、不焚者、龙之母

本篇要介绍的方法，就是所谓“横向拓展”的思路，他结合了三种方法：

1.“类EMD”的模态分解算法：作用是将含噪信号分解为若干IMF,每个IMF反映了信号在不同尺度上的特征。

2.以熵值为特征进行分量筛选：模态分解之后的各个imf分量中，并不是每个分量都含噪声，所以需要进行一步筛选。一般来说，噪声为随机不规则信号，具有较高的样本熵；而有效信号通常具有一定的规律性，样本熵相对较低。通过设定阈值，就可以筛选出需要进行滤波处理的分量了。

3.小波阈值滤波：小波阈值负责对需要降噪的IMF分量实施降噪,去除高频噪声成分。

最后，将降噪后的所有imf分量重构，即可得到滤波结果。

之所以说该算法有着很大的灵活性，就是因为上述每个环节都是有很多调整空间的，比如“类EMD”算法在本专栏中就讲到了EMD、EEMD、CEEMD、CEEMDAN、VMD、EWT、DWT等n多种，熵特征在本专栏中也讲到了功率谱熵、奇异谱熵、能量熵、近似熵、样本熵、模糊熵、排列熵以及他们的多尺度熵和复合多尺度熵，至于小波阈值滤波更是有着很多改进的阈值函数可选或者创造。

在上述众多的排列组合中，本篇以ICEEMDAN-样本熵-改进的小波阈值滤波算法为例[1]。

二、算法流程

下面通过案例来演示算法具体流程。

首先生成一段待降噪信号。

rng(123456)
t = (0:0.001:(1-0.001))';
x1 = 0.6*sin(15*pi*t+pi/5);
x2 = cos(60*pi*t+sin(10*pi*t));
x3 = (1+0.3*cos(10*pi*t)).*sin(200*pi*t);
x4 = wgn(1000,1,-10);
 
fs = 1000; %采样频率
ps = x1+x2+x3;  %未加噪声的纯净信号
s = ps+x4;
figure('color','w')
subplot(2,1,1);plot(t,ps,'k');title('无噪声的仿真信号')
subplot(2,1,2);plot(t,s,'k');title('加入噪声的仿真信号')

这段信号加入噪声前后的图像如下，我们的任务就是将下边的含噪信号尽可能回复成上图中的无噪声信号。

1.类EMD分解

该步骤可以是EMD、EEMD、CEEMD、CEEMDAN、ICEEMDAN、VMD等一系列模态方法中的任意一种，毕竟这一步的目的是将复杂信号分解为一定数量的模态分量。

此案例中我们使用ICEEMDAN分解算法。

Nstd = 0.2; %Nstd为附加噪声标准差与Y标准差之比
NE = 100;   %NE为对信号的平均次数
MaxIter = 1000;% MaxIter 最大迭代次数
imf = pICEEMDAN(sig,1,Nstd,NE,MaxIter);

上边代码中使用了pICEEMDAN函数，这是笔者封装的一个易用的ICEEMDAN画图函数，其介绍可以看之前的文章。分解结果如下：

2.熵特征提取和分量筛选

计算每个IMF分量的样本熵值。 如果大于或等于阈值th，那么它被认为是噪音 IMF；否则，它被认为是IMF的有用信号。 论文中提到[1]，当阈值p设置为0.1，可以有效区分噪声IMF和有用信号IMF。（需注意，该阈值是针对样本熵，如果换其他熵特征，阈值也需要相应调整）

样本熵特征提取可以用我们之前封装的函数，使用这个封装函数，想要换成其他的熵类型也是很简单的，以下是提取样本熵的代码：

featureNamesCell = {'SpEn'}; %要进行特征提取的特征名称，可以根据实际需要进行删减，留下的特征注意拼写正确
 
% 设置样本熵参数，Spdim为样本熵的模式维度，Spr为样本熵的阈值，如果不提取样本熵特征可以删除以下两行
option.Spdim  = 2;
option.Spr   = 0.15;
 
fea = genFeatureEn(imf,featureNamesCell,option);  %调用genFeature函数，完成特征提取，算出的特征值会保存在fea变量里，
 %fea变量的长度和featureNamesCell中指定的特征量一致，且顺序一一对应
 %程序运行完成后，在MATLAB的工作区，双击fea变量，可以查看求得的具体数值

然后我们绘制出计算出的各个imf分量对应的样本熵值：

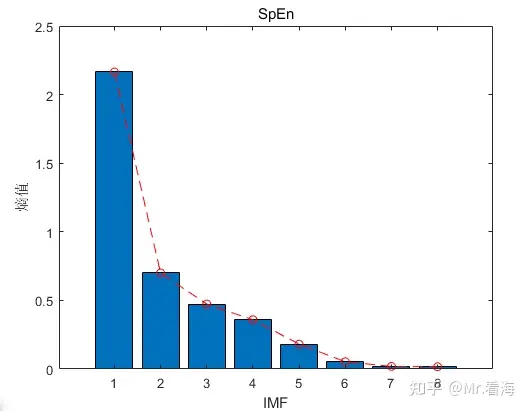
在上述例子中，大于0.1的imf分量为IMF 1~5。

3.使用小波阈值方法对噪声IMF分量进行降噪，并重构

对筛选出的IMF分量使用小波阈值方法进行降噪处理，将去噪后的IMF分量重构,同时将未筛选的IMF分量直接相加,得到最终的去噪结果。

小波阈值降噪的代码实现也很简单，在之前的文章中我们也将小波阈值滤波进行封装，其中还涵盖了5种改进算法：

function s = filterWaveletTh(data,wname,SORH,lev,tptr,options)
% 使用小波阈值法实现滤波，本文件是为了形式统一方便调用的一层封装，具体实现在kwden.m、kwdencmp.m、kwthresh.m、kthselect.m文件中
% 这4个文件均为经本人调整过后的函数文件，原函数分别为wden,wdencmp,wthresh,thselect，所以关于这几个函数更多介绍可以查看对应的官方帮助文档
% 输入：
% data：待滤波数据
% wname：小波名称，可选范围参考这里：https://ww2.mathworks.cn/help/wavelet/ref/wfilters.html?searchHighlight=wname&s_tid=srchtitle_wname_2#d123e130597
% SORH：阈值函数类型
%       sorh ='a1'时，采用改进方法1，改进后的软阈值：
%                     参考论文：孙万麟, 王超. 基于改进的软阈值小波包网络的电力信号消噪[J]. 海军工程大学学报, 2019(4).
%       sorh = 'a2'时，采用改进方法2：
%                     参考论文：刘冲, 马立修, 潘金凤,等. 联合VMD与改进小波阈值的局放信号去噪[J]. 现代电子技术, 2021, 44(21):6.
%       sorh = 'a3'时，采用改进方法4：
%                     参考论文：基于改进小波阈值-CEEMDAN算法的ECG信号去噪研究
%       sorh = 'a4'时，采用改进方法3：
%                     参考论文：基于改进小波阈值函数的语音增强算法研究
%                     采用该方法需要输入两个调节因子，分别是alpha和gamma，取alpha>0，0<gamma<1
%       sorh = 'a5'时，采用改进方法3：
%                     参考论文：基于VMD与改进小波阈值的地震信号去噪方法研究
%                     采用该方法需要输入两个调节因子，分别是alpha和beta% lev：  小波分解水平
% tptr： 阈值选择规则，有可选类型：
%       '' — Adaptive threshold selection using the principle of Stein's Unbiased Risk Estimate (SURE).
%       'sqtwolog' — Fixed-form threshold is sqrt(2*log(length(X))).
%       'heursure' — Heuristic variant of 'rigrsure' and 'sqtwolog'.
%       'minimaxi' — Minimax thresholding.
%       'visushrink' - 通用阈值去噪方法
% options：部分阈值函数需要补充的参数设置，即某些调节因子，需要用结构体方式调用幅值，如options.a4_alpha=2。如果不需要设置，可以赋值为options=[]。具体如下：
%          -a4_alpha：改进方法4的alpha值设置
%          -a4_gamma：改进方法4的gamma值设置
%          -a5_alpha：改进方法5的alpha值设置
%          -a5_beta：改进方法5的beta值设置
% 输出：
% s：经过滤波后得到的数据
% 理论讲解见：https://zhuanlan.zhihu.com/p/579187348/

调用上述函数，对每个含噪声的分量进行降噪。滤波前后对比图如下：

算法主要对IMF1和IMF2起了作用

将上述IMF1-5滤波点后的结果重构；对于IMF6及以后的分量，由于其中不含噪声，所以直接进行重构即可。

最终滤波结果如下：

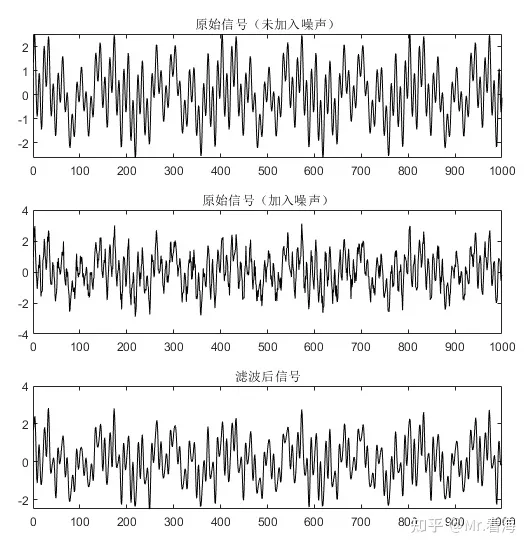
计算得到，滤波后的SNR、MSE和NCC值分别为：12.2486、0.071741、0.97004

效果还是可以的。上述结果我没有花太多时间做调试，如果大家精心调试修改，可以得到更好的滤波结果。

三、MATLAB封装实现

上述流程中调用了EMD分解、熵特征提取、小波阈值这三种算法，总体流程还是比较长的，为了方便大家使用，我将其流程进行了二次封装，对于上述ICEEMDAN-样本熵-小波阈值降噪方法，只需要一行代码就可以实现：

reSig = filEMDsWaveletTh(x); %sig 为待滤波信号；reSig 为滤波后的信号

当然，如果大家想要替换其中的部分算法进行改进，只需要在这个封装函数中进行修改就行，替换起来还是很简单的~

需要上边这个filEMDsWaveletTh函数文件以及测试代码的同学，可以在公众号 khscience（看海的城堡）中回复“EMD小波阈值”获取。文章中绘制图片的代码也在其中哦~

扩展阅读

Mr.看海：【滤波专题-第4篇】滤波器滤波效果的评价指标（信噪比SNR、均方误差MSE、波形相似参数NCC）

Mr.看海：【滤波专题-第6篇】小波阈值去噪方法看这一篇就明白了~（附MATLAB实现）

Mr.看海：【滤波专题-第7篇】“类EMD”算法分解后要怎样使用（3）——EMD降噪方法及MATLAB代码实现

Mr.看海：这篇文章能让你明白经验模态分解（EMD）——EMD在MATLAB中的实现方法

Mr.看海：类EMD的“信号分解方法”及MATLAB实现（第一篇）——EEMD

Mr.看海：类EMD的“信号分解方法”及MATLAB实现（第二篇）——CEEMD

Mr.看海：类EMD的“信号分解方法”及MATLAB实现（第三篇）——CEEMDAN

Mr.看海：类EMD的“信号分解方法”及MATLAB实现（第四篇）——VMD

Mr.看海：类EMD的“信号分解方法”及MATLAB实现（第五篇）——ICEEMDAN

Mr.看海：类EMD的“信号分解方法”及MATLAB实现（第七篇）——EWT

Mr.看海：类EMD的“信号分解方法”及MATLAB实现（第八篇）——离散小波变换DWT（小波分解）

参考

1. ^ab[1]师雪玮,徐大林,刘志成.基于ICEEMDAN和小波阈值的Φ-OTDR信号去噪算法[J/OL].指挥控制与仿真,1-7[2024-03-14].http://106.53.219.187:8085/kcms/detail/32.1759.TJ.20231214.1421.004.html.