深度学习——权重衰减（weight_decay)_权重衰减是lrf吗

深度学习——权重衰减（weight_decay)

---

前言

上一章描述了过拟合的问题，本章我们将介绍一些正则化模型的技术。如权重衰减

参考书：
《动手学深度学习》

---

一、权重衰减

1.1. 范数与权重衰减

在训练参数化机器学习模型时，权重衰减（weight decay）是最广泛使用的正则化的技术之一， 它通常也被称为$L_2$正则化。这项技术通过函数与零的距离来衡量函数的复杂度，

因为在所有函数$f$中，函数$f=0$（所有输入都得到值$0$），在某种意义上是最简单的。

但是我们应该如何精确地测量一个函数和零之间的距离呢？

一种简单的方法是通过线性函数
$f(\mathbf{x})={\mathbf{w}}^{\top }\mathbf{x}$ 中的权重向量的某个范数来度量其复杂性，
例如$\Vert \mathbf{w}{\Vert }^2$。

要保证权重向量比较小，最常用方法是将其范数作为惩罚项加到最小化损失的问题中：
即将原来的训练目标最小化训练标签上的预测损失，调整为最小化预测损失和惩罚项之和。

现在，如果我们的权重向量增长的太大，我们的学习算法可能会更集中于最小化权重范数$\Vert \mathbf{w}{\Vert }^2$。这正是我们想要的。

我们的损失由下式给出：
​
$$L(\mathbf{w},b)=\frac{1}{n}\sum _{i=1}^n\frac{1}{2}{\left({\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}+b-y^{(i)}\right)}^2.$$

为了惩罚权重向量的大小，我们必须以某种方式在损失函数中添加$\Vert \mathbf{w}{\Vert }^2$

但是模型应该如何平衡这个新的额外惩罚的损失？
实际上，我们通过正则化常数$\lambda$来描述这种权衡，这是一个非负超参数，我们使用验证数据拟合：

$$L(\mathbf{w},b)+\frac{\lambda }{2}\Vert \mathbf{w}{\Vert }^2,$$

对于$\lambda >0$，我们限制$\Vert \mathbf{w}\Vert$的大小。

为什么在这里我们使用平方范数而不是标准范数（即欧几里得距离）？

我们这样做是为了便于计算。通过平方$L_2$范数，我们去掉平方根，留下权重向量每个分量的平方和。
这使得惩罚的导数很容易计算：导数的和等于和的导数。

此外，为什么我们首先使用$L_2$范数，而不是$L_1$范数。

$L_2$正则化线性模型构成经典的岭回归（ridge regression）算法，
$L_1$正则化线性回归是统计学中类似的基本模型，通常被称为套索回归（lasso regression）。

使用$L_2$范数的一个原因是它对权重向量的大分量施加了巨大的惩罚。这使得我们的学习算法偏向于在大量特征上均匀分布权重的模型。在实践中，这可能使它们对单个变量中的观测误差更为稳定。

相比之下，$L_1$惩罚会导致模型将权重集中在一小部分特征上，
而将其他权重清除为零。这称为特征选择（feature selection），可能是其他场景下需要的。

$L_2$正则化回归的小批量随机梯度下降更新如下式：

w ← ( 1 − η λ ) w − η ∣ B ∣ ∑ i ∈ B x ( i ) ( w ⊤ x ( i ) + b − y ( i ) ) .

$$\begin{aligned} \mathbf{w} & \leftarrow \left(1- \eta\lambda \right) \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \mathbf{x}^{(i)} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right). \end{aligned}$$ w​←(1−ηλ)w−∣B∣η​i∈B∑​x(i)(w⊤x(i)+b−y(i)).​

我们根据估计值与观测值之间的差异来更新$\mathbf{w}$。然而，我们同时也在试图将$\mathbf{w}$的大小缩小到零。
这就是为什么这种方法有时被称为权重衰减。我们仅考虑惩罚项，优化算法在训练的每一步衰减权重。

与特征选择相比，权重衰减为我们提供了一种连续的机制来调整函数的复杂度。 较小的$\lambda$值对应较少约束的$\mathbf{w}$，而较大的$\lambda$值对$\mathbf{w}$的约束更大。

是否对相应的偏置$b^2$进行惩罚在不同的实践中会有所不同，
在神经网络的不同层中也会有所不同。通常，网络输出层的偏置项不会被正则化。

1.2. 高维线性回归

我们通过一个简单的例子来演示权重衰减。

首先，我们像以前一样生成一些数据，生成公式如下：

$$y=0.05+\sum _{i=1}^{d}0.01x_i+ϵ\text{ where }ϵ\sim \mathcal{N}(0,0.01^2).$$

我们选择标签是关于输入的线性函数。标签同时被均值为0，标准差为0.01高斯噪声破坏。
为了使过拟合的效果更加明显，我们可以将问题的维数增加到$d=200$，
并使用一个只包含20个样本的小训练集。

import torch
from d2l import torch as d2l
from torch import nn

n_train,n_test,num_inputs,batch_size = 20,100,200,5
true_w,true_b = torch.ones((num_inputs,1))*0.01,0.05


"""
使用d2l.synthetic_data函数生成了训练数据和测试数据，并使用d2l.load_array函数将数据加载为迭代器。
"""
train_data = d2l.synthetic_data(true_w,true_b,n_train)
train_iter = d2l.load_array(train_data,batch_size)


test_data = d2l.synthetic_data(true_w,true_b,n_test)
test_iter = d2l.load_array(test_data,batch_size,is_train= False)
#这里设置is_train=False表示测试数据不用于模型训练，只用于评估模型的性能。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

1.3. 从零开始实现

下面我们将从头开始实现权重衰减，只需将$L_2$的平方惩罚添加到原始目标函数中。

1.3.1.初始化模型参数

#初始化模型参数
#我们将定义一个函数来随机初始化模型参数
def init_params():
    w = torch.normal(0,1,size=(num_inputs,1),requires_grad= True)
    b = torch.zeros(1,requires_grad=True)
    return [w,b]
1
2
3
4
5
6

1.3.2. 定义L₂范数惩罚

#定义L2范数惩罚（实现这一惩罚最方便的方法是对所有项求平方后并将它们求和）
def l2_penalty(w):
    return torch.sum(w.pow(2))/2 #将权重w的平方和除以2,除以2是为了方便计算梯度

1
2
3
4
5

1.3.3. 定义训练代码实现

#定义训练代码实现
def train(lambd):
    w,b  = init_params()
    net,loss = lambda x: d2l.linreg(x,w,b),d2l.squared_loss
    num_epochs,lr = 100,0.003
    animator = d2l.Animator(xlabel="epochs",ylabel="loss",yscale="log",xlim= [5,num_epochs],legend=["train","test"])
    for epoch in range(num_epochs):
        for x,y in train_iter:
            #增加了L2范数惩罚项
            #广播机制使l2_penalty(w)成为一个长度为batch_size的向量
            l = loss(net(x),y) + lambd * l2_penalty(w)
            l.sum().backward()
            d2l.sgd([w,b],lr,batch_size)
        if (epoch+1)%5 ==0:
            animator.add(epoch+1,(d2l.evaluate_loss(net,train_iter,loss),
                                d2l.evaluate_loss(net,test_iter,loss)))
    print("w的L2范数是：",torch.norm(w).item())
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

1.3.4. 不管正则化直接训练

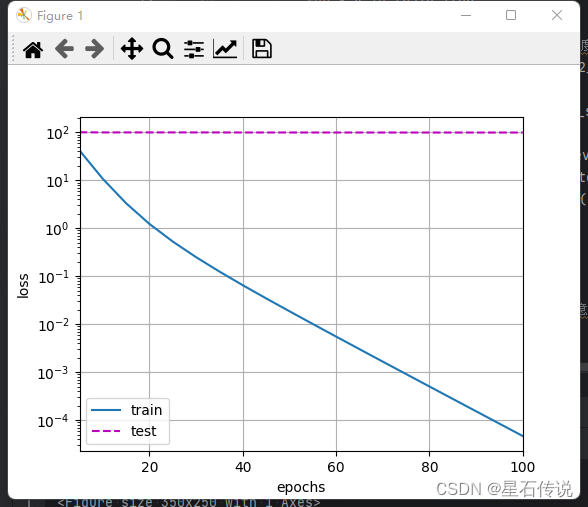
#现在用`lambd = 0`禁用权重衰减后运行这个代码。
#注意，这里训练误差有了减少，但测试误差没有减少，这意味着出现了严重的过拟合。

train(lambd= 0)

#结果：
w的L2范数是： 13.981727600097656

1
2
3
4
5
6
7
8

1.3.5. 使用权重衰减

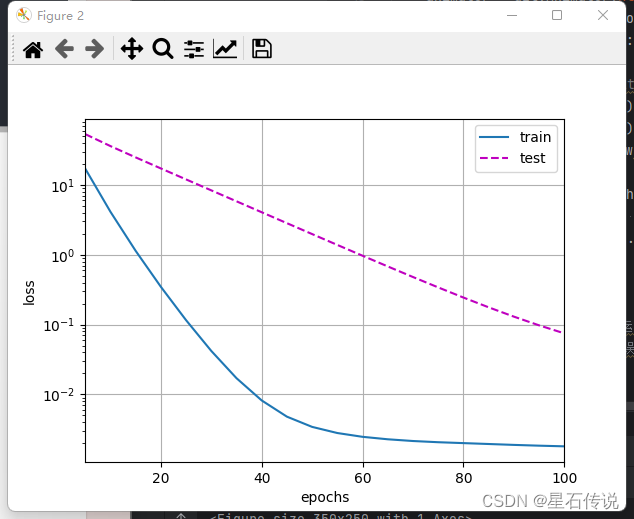
#使用权重衰减来运行代码。
#注意，在这里训练误差增大，但测试误差减小。这正是我们期望从正则化中得到的效果。

train(lambd= 3)

#结果：
w的L2范数是： 0.3319331705570221

d2l.plt.show()

1
2
3
4
5
6
7
8
9
10

1.4. 简洁实现

深度学习框架为了便于我们使用权重衰减，将权重衰减集成到优化算法中，以便与任何损失函数结合使用。

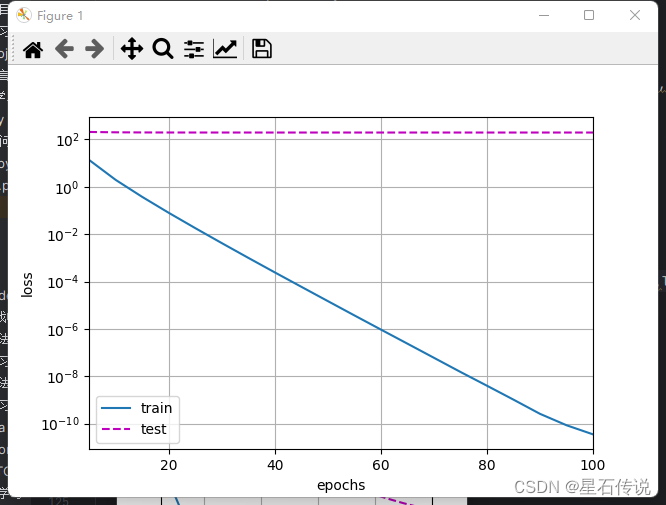
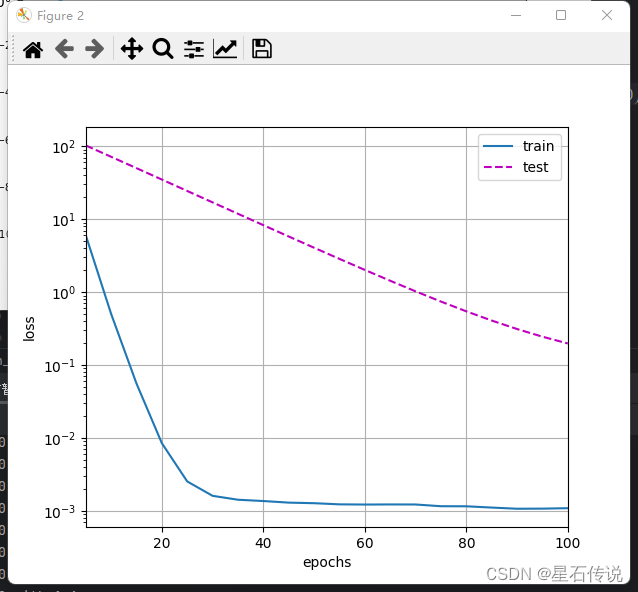
#在下面的代码中，我们在实例化优化器时直接通过`weight_decay`指定weight decay超参数。
#默认情况下，PyTorch同时衰减权重和偏移。
#这里我们只为权重设置了`weight_decay`，所以偏置参数$b$不会衰减。

def train_concise(wd):
    net = nn.Sequential(nn.Linear(num_inputs,1))
    for param in net.parameters():
        param.data.normal_() #使用正态分布随机初始化参数
    loss = nn.MSELoss(reduction="none") #定义损失函数为均方误差损失
    num_epochs,lr = 100,0.003
    #偏置参数没有衰减
    trainer = torch.optim.SGD(
        [{"params":net[0].weight,"weight_decay":wd},
         {"params":net[0].bias}],lr = lr
    )  #net[0].weight表示模型的权重参数，net[0].bias表示模型的偏置参数。weight_decay参数用于设置权重衰减的强度。
    animator = d2l.Animator(xlabel="epochs",ylabel="loss",yscale="log",xlim=[5,num_epochs],
                            legend=["train","test"])
    for epoch in range(num_epochs):
        for x,y in train_iter:
            trainer.zero_grad() #清零梯度，以防止梯度累积
            l = loss(net(x),y)
            l.mean().backward() #计算损失的平均值，并进行反向传播，计算梯度
            trainer.step() #更新模型的参数，执行一步优化器的更新

        if (epoch+1)%5 == 0:
            animator.add(epoch+1,(d2l.evaluate_loss(net,train_iter,loss),d2l.evaluate_loss(net,test_iter,loss)))
    print("w的L2范数：", net[0].weight.norm().item())  #打印模型权重的L2范数，用于评估模型的复杂度。



train_concise(0)
train_concise(3)
d2l.plt.show()

#结果：
w的L2范数： 13.411089897155762
w的L2范数： 0.3319282829761505

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

---

总结

为了有效防止模型的过拟合，降低模型的复杂度，提高泛化能力，本章简单记录了一种常见的正则化技术：权重衰减。简单来说权重衰减是通过在损失函数中添加一个正则化项来实现的。这个正则化项通常是模型参数的L2范数（平方和）或L1范数（绝对值和），通过限制模型参数的大小来防止过拟合。

我独泊兮其未兆，如婴儿之未孩，傫傫（lèi lèi）兮，若无所归。

–2023-10-2 进阶篇