详解快速傅里叶变换FFT_分析一般信号fft的频谱特点

1. 频谱图的特征

频谱是离散的，虽然看起来曲线像是连续的，但实际上是由一条条离散的谱线上的幅值连成看起来像连续的曲线。谱线的总数目由FFT分析点数决定，也就是说，如果一次FFT分析N个数据点，那么，得到的频谱图由N/2条谱线组成的。相邻两条谱线之间的频率间隔称为频率分辨率，因此，谱线只位于频率分辨率的整数倍频率处。由FFT计算得到的频谱结果数值只位于这些谱线处，相邻谱线中间没有任何计算结果，我们把这种效应称为栅栏效应。因此，频率分辨率对频谱有两点明显影响：第一，影响频率精度；第二，影响频谱幅值。   

由于频率成分是按四舍五入的方式归到邻近的谱线上，因此，从频谱图中获得的频率成分与真实值之间的误差在 -～ 之间。可以看出，频率分辨率越精细（数值越小），频率精度越高。但是，我们知道，频率分辨率与时间成反比，当频率分辨率越精细时，一帧时域数据越长，这会影响数据截断次数和平均次数。不管怎样，频谱图中的频率总是与真实值有差异，除了一种极少出现的特殊情况：压谱线采样。另外，频率分辨率的大小也会决定着谱线数，对于有的频谱而言，如随机信号的频谱spectrum与自谱autopower linear等，会出现谱线数越多，幅值越低的现象。

除了频率分辨率会影响频率幅值之外，泄漏对幅值也有影响。由于信号截断导致数据不满足傅里叶周期性变换要求而出现频谱泄漏，泄漏的表现是频谱出现拖尾效应：信号的幅值能量泄漏到邻近的谱线上，或者说，需要更多的谱线才能近似这个信号。这样一来，信号的幅值与真实之间存在差异，为了减少泄漏，需要加窗函数，但加窗只能减少泄漏，不能消除泄漏，因此，加窗后的信号幅值仍与真实值有差异。为了减少二者之间的差异，需要进行幅值修正或能量修正。因此，后续在求频谱图的窄带有效值或Overall level时需要考虑修正形式。

频谱图中每条谱线对应的频率成分都是一个单频信号，因此，具有振动三要素：幅值、频率和相位。频谱图中的频率成分可能是由以下几个方面引起的：共振、转频及其倍频、特征频率（阶次）、工频及其倍频、调制产生的边频、和频与差频、异常频率等等。

下图显示的载波频率为930Hz，输入和输出的转频分别为30Hz和34.4Hz，因此，在以啮合频率为载波频率的两侧包含了以两个转频为调制频率的边频带。同时，又存在以两个转频的差频4.4Hz为调制频率的边频带，此时的载波频率为输入转频对应的边频带频率，这是明显的交叉调制现象。如果载波频率的幅值和两侧边频带幅值相差很大，在图形显示时可以用分贝尺度。

图 调制引起的边频中的差频

频率相近的分量容易形成和频与差频，这是这些频率交叉调制的结果。如主动轮和从动轮的齿数相差不大，导致输入转频与输出转频交叉调制形成和频或差频，如图8所示的4.4Hz，则是输入转频与输出转频的差频。另外，和频与差频不一定是一次谐波频率之和或之差，也可能是其他谐波频率，也可能是其中一个是一次谐波频率，而另一个是高次谐波频率。

异常频率与结构特性、转速没有关系，如齿轮中的鬼线频率。一般这类异常频率有两个方法可用于确定，方法一是基于异常频率对负荷不敏感，因此，不同的负载下，但异常频率变化小。方法二是使用阶次分析，这样可以通过阶次线确定异常频率与转速的倍数关系，如果这个倍数不是任何部件的阶次，那么可以确定这个频率就是异常频率。如果发现一个频率（或一组谐频）找不出来源，那么有理由怀疑它是异常频率。

相位曲线

以最为简单的质量-弹簧表示的单自由度系统（见图2）为例来说明。这个单自由度系统的位移方程为 y=Asin(ωt+90°)，式中A表示幅值，ω是振动频率，ωt+90°表示的是随时间变化的相位，而90°表示的是初始相位，简称初相位。90°表示质量块在运动的初始时刻位于正向最大位移处，也就是离平衡位置正向最远处。从表达式可以看出，相位是时间的函数，因此，随着时间的推进，相位时刻发生变化，而在空间位置上，质量块的位置相应地随着相位时刻发生变化。时间不同，相位不同，质量块所处的空间位置不同，而初相位始终保持不变。因此，相位是在给定时刻振动体测量点相对于固定参考点的位置，单位是度［°］。在这个例子中，固定的参考点是质量块的平衡位置。因此，相位表明了质量块在时间与空间上的位置关系。

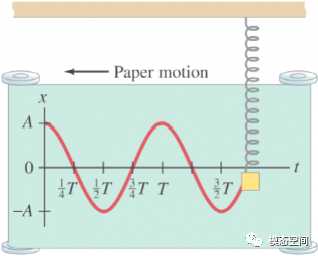
图2 质量-弹簧系统的位移轨迹

从这个例子可以看出，当质量块运动到空间不同位置时，其相位是不同的。或者说，相位是振动在空间位置上相互差异的标志。另一方面，相位也是振动在时间先后关系上的标志。如果对图2所示的运动位移轨迹移动1/4个周期，得到如图3所示的运动轨迹，因此，时间移动表示的是相位的移动，反之亦然。这是针对同一个振动体而言，在不同的振动体或不同部件之间的振动也有这样的关系。两个振动之间的差异体现的是时间差异或空间位置差异。

图3 在图2的基础上时间移动1/4个周期

因此，相位是同一部件不同位置处的振动或不同部件之间的振动在时间先后关系上或空间位置关系上相互差异的标志。

对于旋转部件而言，每旋转一圈，表示转过360°，因此，两个振动之间的相位差就是转过此角度的时间差。通过角度不仅表示空间、而且表示时间，这便是相位的奥妙之处。

绝对相位

对于旋转机械，经常利用旋转部件上已有的键槽、凹孔或人为粘贴反光纸，同时安装键相探头来获取旋转部件的键相信号，探头每经过这些位置，便触发一个脉冲信号（与转速测量类似），如图4所示。脉冲信号是确定旋转部件上各测点各个振动频率（如1频、2倍频、0.5倍频…）相位的基准，脉冲频率与旋转部件的旋转频率完全同步，通过此键相信号来确定旋转部件在时间与空间上的位置。

图4 键相信号

我们把从键相器脉冲信号触发到某个特定频振动信号（如1频、2倍频、0.5倍频…）第一个正峰值之间的角度，称为绝对相位。绝对相位是具体测得的相位，习惯上简称相位。说“某测点、某频率的相位为某某度”指的就是绝对相位，也就是相对于轴上固定标志通过键相探头的那一时刻及位置，此频率的最大振动与该测振探头之间的角度。由键槽和键相探头的位置及转子旋转方向，绝对相位还能给出最大振动具体的空间方位。

相位差（相对相位）

相位差是两个振动的相位之差。而相对相位是两个振动信号波形最近对应点（如波峰与波峰）之间的角度，如图2与图3两个信号的相对相位为90°。在实际应用中，往往并不讲相对相位，而只讲相位差，是因为实际上已经将相对相位所强调的“最近的对应点” 溶进了相位差中。例如，假设A点、B点相位分别为31°、346°，它们之间的相位差既可以讲为315°，也可以讲为45°。

通过相位差，可以很具体地想象到两个振动矢量在时间和空间上的相互关系：

1. 谁先谁后：相位小的在先、称超前，相位大的在后、称滞后，因为相位小的先到达第一个正峰、即最大振动点处。对于图2所示的单自由度系统而言，其振动位移、速度和加速度三者之间的相位关系如图5所示，我们称振动速度超前振动位移90°，振动加速度超前振动速度90°，振动加速度超前振动位移180°。从图中可以看出，在0时刻之后，加速度最先达到正峰，然后是速度，最后才是位移。                                                               图5 振动位移、速度和加速度三者之间的相位关系

2. 相差的时间t：t＝相位差×周期/360°＝相位差/(频率×360°)，实际中很少算，主要是由相位差（角度）的大小想象两者间隔时间的长短。对于图2和图3的信号，我们知道，二者相位相差了90°，对应的时间差为1/4个周期。另外，也可以利用相位差来计算信号的时间延迟。

3. 空间位置：相位差就是空间方向差夹角的角度。特别对于有键相信号的旋转部件测量得到的振动信号，这一点更易于理解。

4. 相位差表面上看是一个角度，实际上是反映了两个振动在时间先后关系上或空间位置关系上，是否存在差异、存在什么差异、存在多大差异。在分析振动原因和判断振动故障类型时，往往更关注相位差，而不是相位。

相位差是两个振动的相位之差。而相对相位是两个振动信号波形最近对应点（如波峰与波峰）之间的角度，如图2与图3两个信号的相对相位为90°。在实际应用中，往往并不讲相对相位，而只讲相位差，是因为实际上已经将相对相位所强调的“最近的对应点” 溶进了相位差中。例如，假设A点、B点相位分别为31°、346°，它们之间的相位差既可以讲为315°，也可以讲为45°。