devbox
花生_TL007
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

十大排序——11.十大排序的比较汇总及Java中自带的排序算法

作者：花生_TL007 | 2024-04-17 07:13:13

赞

踩

十大排序——11.十大排序的比较汇总及Java中自带的排序算法

这篇文章对排序算法进行一个汇总比较！

目录

0.十大排序汇总

0.1概述

0.2比较和非比较的区别

0.3基本术语

0.4排序算法的复杂度及稳定性

1.冒泡排序

算法简介

动图演示

代码演示

应用场景

算法分析

2.快速排序

算法简介

动图演示

代码演示

应用场景

算法分析

3.插入排序

算法简介

动图演示

代码演示

应用场景

算法分析

4.选择排序

算法简介

动图演示

代码演示

应用场景

算法分析

5.归并排序

算法简介

图片演示

代码演示

应用场景

算法分析

6.希尔排序

算法简介

图片演示

代码演示

应用场景

算法分析

7.堆排序

算法简介

图片演示

代码演示

应用场景

算法分析

8.计数排序

算法分析

动图演示

代码演示

应用场景

算法分析

9.基数排序

算法分析

动图演示

代码演示

应用场景

算法分析

10.桶排序

算法分析

动图演示

代码演示

应用场景

算法分析

11.Java自带的排序算法

0.十大排序汇总

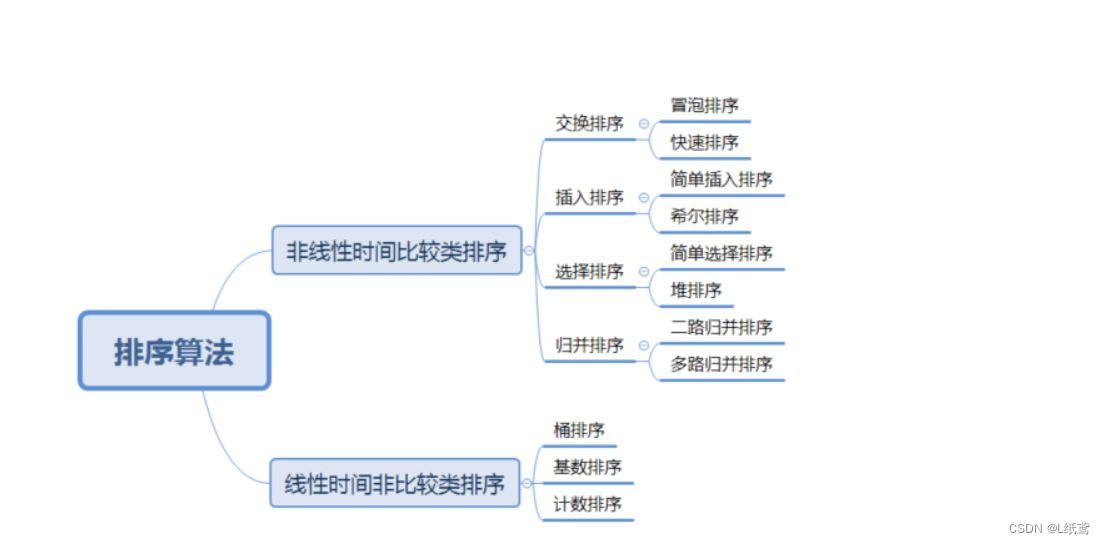
0.1概述

一图以蔽之：

0.2比较和非比较的区别

常见的快速排序、归并排序、堆排序、冒泡排序等属于比较排序。在排序的最终结果里，元素之间的次序依赖于它们之间的比较。每个数都必须和其他数进行比较，才能确定自己的位置。


在冒泡排序之类的排序中，问题规模为 n，又因为需要比较 n 次，所以平均时间复杂度为O(n²)。

在归并排序、快速排序之类的排序中，问题规模通过分治法消减为 logN 次，所以时间复杂度平均O(nlogn)。


比较排序的优势是：适用于各种规模的数据，也不在乎数据的分布，都能进行排序。可以说，比较排序适用于一切需要排序的情况。


计数排序、基数排序、桶排序则属于非比较排序。非比较排序是通过确定每个元素之前，应该有多少个元素来排序。针对数组 arr，计算 arr 之前有多少个元素，则唯一确定了 arr 在排序后数组中的位置。


非比较排序只要确定每个元素之前的已有的元素个数即可，所有一次遍历即可解决。算法时间复杂度O(n)。


非比较排序时间复杂度底，但由于非比较排序需要占用空间来确定唯一位置。所以对数据规模和数据分布有一定的要求。

0.3基本术语

稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面；
不稳定：如果a原本在b的前面，而a=b，排序之后a可能出现在b的后面；
内排序：所有的排序操作都在内存中完成；
外排序：由于数据太大，因此把数据放在磁盘中，而排序通过磁盘和内存的数据传输才能进行；
时间复杂度：一个算法执行所消耗的时间；
空间复杂度：运行完一个程序所需内存的大小。

0.4排序算法的复杂度及稳定性

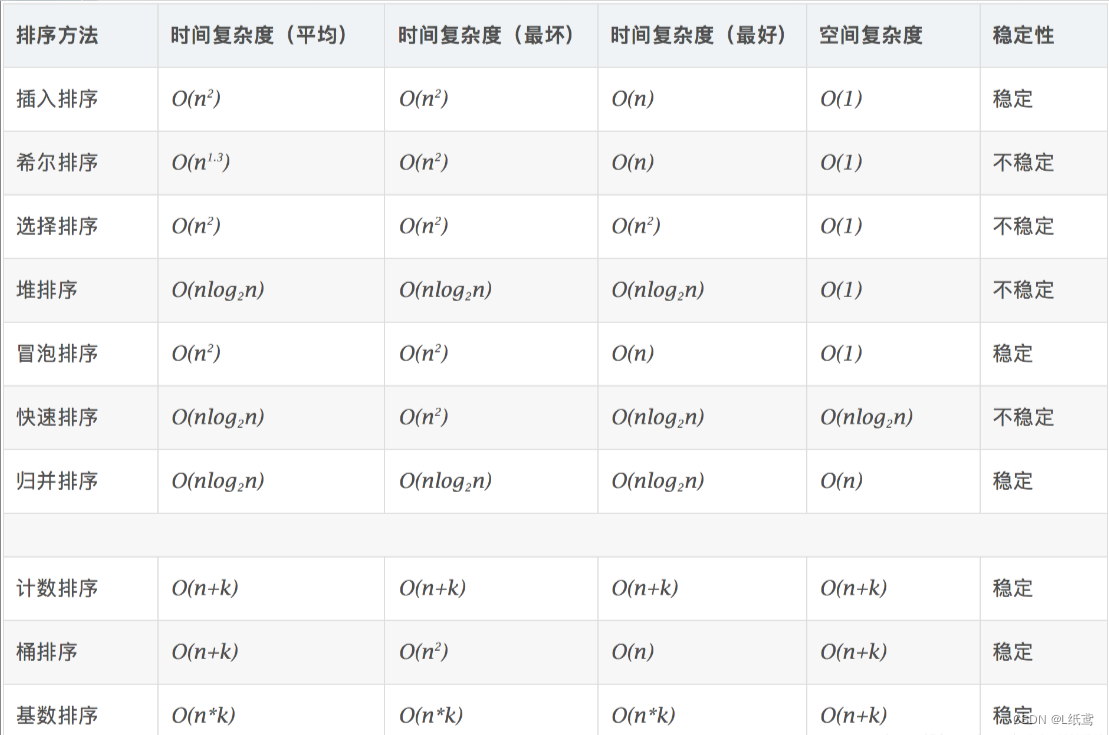
1.冒泡排序

算法简介

1. 从左向右依次对比相邻元素，将较大值交换到右边；
2. 每一轮循环可将最大值交换到最左边
3. 重复1.2两个步骤，直至完成整个数组。

动图演示

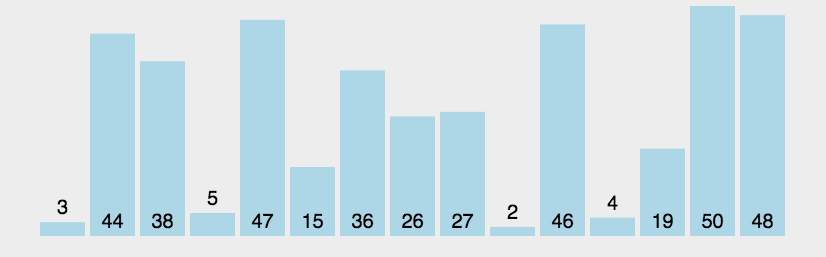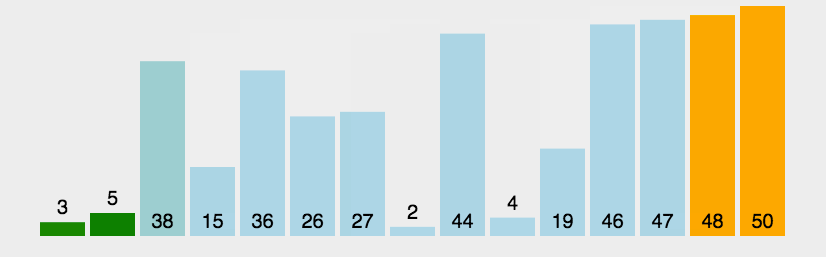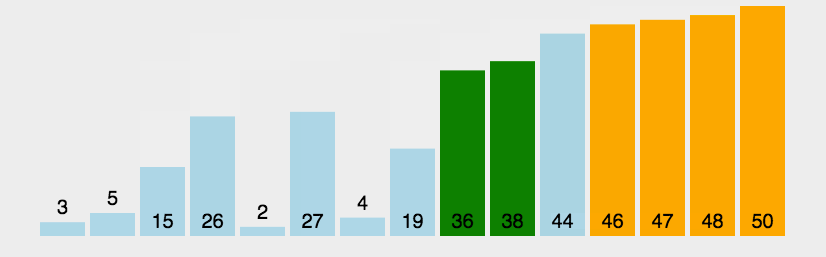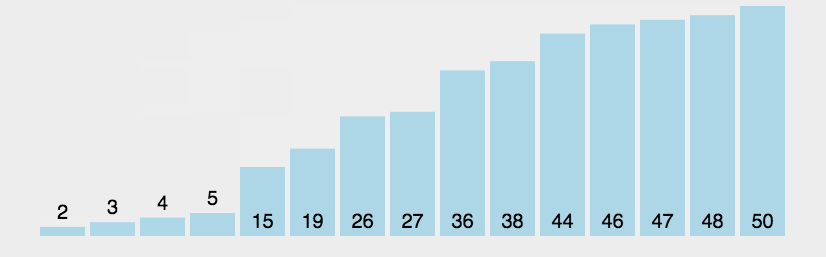
代码演示

  1. package Sorts;
  2.  
  3. import java.util.Arrays;
  4. //冒泡排序
  5. public class MaoPaoSort {
  6.     public static void main(String[] args) {
  7.         int[] arr = new int []{5,9,2,7,3,1,10};
  8.         maoPaoSort(arr);
  9.         System.out.println(Arrays.toString(arr));
  10.     }
  11.  
  12.     public static void maoPaoSort(int[]arr){
  13.         for (int i = 0; i <arr.length ; i++) {
  14.             for (int j = 0; j <arr.length-1 ; j++) {
  15.                 if (arr[j] > arr[j+1]){//这是比较相邻的元素
  16.                     int temp = arr[j];
  17.                     arr[j]=arr[j+1];
  18.                     arr[j+1]=temp;
  19.                 }
  20.             }
  21.         }
  22.     }
  23. }

应用场景

一般在学习的时候作为理解排序原理的时候使用，在实际应用中不会使用

算法分析

最佳情况：T ( n ) = O ( n )

最差情况：T ( n ) = O ( n^2 )

平均情况：T ( n ) = O ( n^2 )

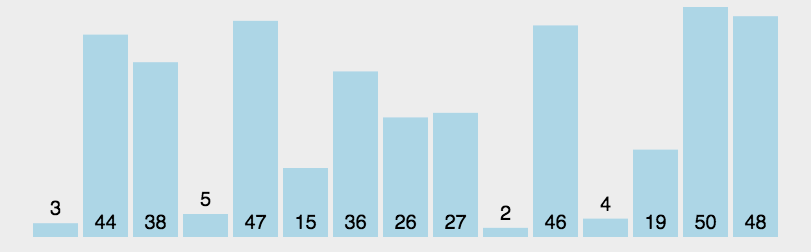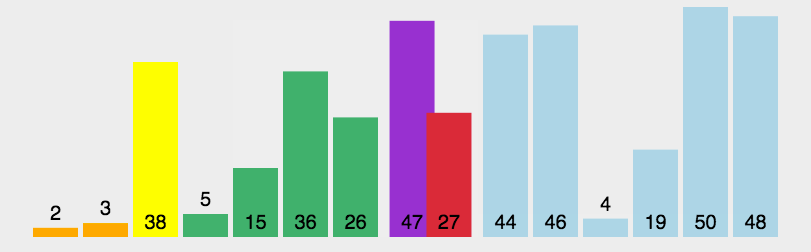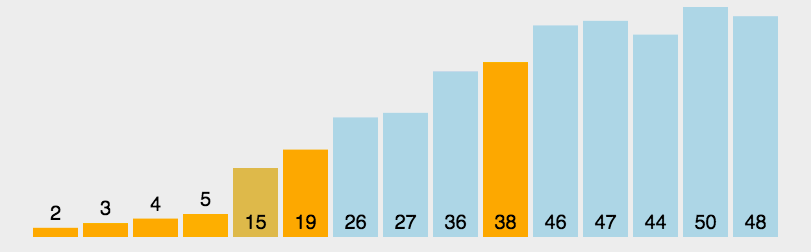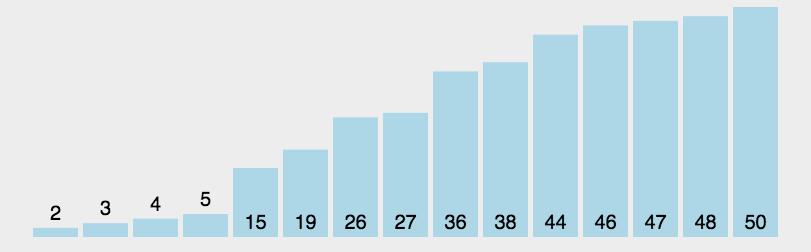
2.快速排序

算法简介

  1. 选择一个元素赋值给中间元素temp，默认选择左边第一个元素，这样左边第一个元素的位置就空出来了；
  2. 先从最右边的元素开始依次跟temp比较大小，大于等于temp元素的原地不动，遇到小于temp元素的则终止循环，把该元素赋值到左侧空出来的位置，同时左侧索引值自增，这是该元素原来的位置就空出；
  3. 然后左侧元素开始依次跟temp比较大小，小于等于temp元素的原地不动，遇到大雨temp元素的则终止循环，把该元素赋值到右侧空出来的位置，同时右侧索引值自减；
  4. 依次循环2,3步，直至左侧索引等于右侧索引，则完成一轮循环，把哨兵赋值到该索引的位置。
  5. 在分别递归地对 temp 左右两侧的子数组进行1234步，直至递归子数组只有一个元素则排序完成

动图演示

代码演示

  1. package Sorts;
  2.  
  3. import java.util.Arrays;
  4. import java.util.concurrent.ThreadLocalRandom;
  5. //快排
  6. public class QuickSort {
  7.     public static void main(String[] args) {
  8.         int[] array = {16,13,7,15,28,11,9,32,22,19};
  9.         int[] array1 = {4,2,1,3,2,4};
  10.         System.out.println("排序前："+ Arrays.toString(array1));
  11.         sort(array1);
  12.         System.out.println("排序后："+ Arrays.toString(array1));
  13.  
  14.     }
  15.     /**
  16.      * 交换操作
  17.      * */
  18.     private static void swap(int[] array,int i,int j){
  19.         int t = array[i];
  20.         array[i] = array[j];
  21.         array[j] = t;
  22.     }
  23.     /**
  24.      * 排序的函数
  25.      * */
  26.     private static void sort(int[] array) {
  27.         quick(array,0,array.length-1);
  28.     }
  29.     /**
  30.      * 递归的函数
  31.      * */
  32.     private static void quick(int[] array, int left, int right) {
  33.         //结束递归的条件，如果我们左边的索引大于或等于右边的索引了（最多只能等于，不可能大于），那说明就只有一个元素的了，那就不用递归了
  34.         if (left>=right){
  35.             return;
  36.         }
  37.         int p = partition4(array,left,right); //p代表基准点元素的索引
  38.         quick(array,left,p-1); // 对基准点左边的区进行递归操作
  39.         quick(array,p+1,right); // 对基准点右边的区进行递归操作
  40.     }
  41.     /**
  42.      * 分区并进行比较然后排序的函数（这部分是核心代码）
  43.      * 单边快排
  44.      * */
  45.     private static int partition1(int[] array, int left, int right) {
  46.         int pv = array[right]; //基准点的值
  47.         int i = left;
  48.         int j = left;
  49.         while (j<right){ //当j小于右边届的时候，j就要+1
  50.             if (array[j]<pv){ //j找到比基准点小的值
  51.                 if (i!=j){
  52.                     swap(array,i,j);
  53.                 }
  54.                 /**
  55.                  * 这里多说一点
  56.                  * i与j都是从left开始的，初始指向是一致的，i找大的，j找小的
  57.                  * 进入这个判断，就是说明j找到小的了
  58.                  * 没进入这个判断，就是说明j没有找到小的，也就是说此时j指向的值大于等于基准值
  59.                  * 因为i与j的指向在初始时是一致的
  60.                  * 所以没进入这个判断时，i指向的值就比基准值大了
  61.                  * 所以i就找到了，不用+1了
  62.                  * 但是j没有找到
  63.                  * 所以j要+1
  64.                  * 这就是i++在里面；j++在外面的原因
  65.                  * 如果进入这个判断，即j找到小的了，此时i在哪？
  66.                  * i在j前面或者和i在同一个位置，看代码就能想清楚
  67.                  * 有没有可能j找到小的了，然后不走了，i没找到继续走，然后在j后面找到大的了？
  68.                  * 这种情况就没必要交换了，并且这种情况进不来这个判断
  69.                  * */
  70.                 i++;
  71.             }
  72.             j++;
  73.         }
  74.         swap(array,i,right); //交换基准点与i的位置，此时i记录的就是基准点的位置
  75.         return i;
  76.     }
  77.     /**
  78.      * 双边快排
  79.      * */
  80.     private static int partition2(int[] array, int left, int right) {
  81.         int pv = array[left]; //基准点的值
  82.         int i = left; //游标i，从最左边开始，找大的
  83.         int j = right; //游标j，从最右边开始，找小的
  84.  
  85.         while (i < j){ //i<j的时候进行循环，一旦i=j或i>j，就要退出循环
  86.             while (i < j && array[j] > pv){//找比基准点小的值，没找到j就--，一旦找到，就退出循环
  87.                 j--;
  88.             }
  89. //            while (i<j && array[i]<pv)
  90.             while (i<j && array[i]<=pv){//找比基准点大的值，没找到i就++，一旦找到，就退出循环
  91.                 i++;
  92.             }
  93.             swap(array,i,j);//交换
  94.         }
  95.         swap(array,left,i);
  96.         return i;
  97.     }
  98.     /**
  99.      * 定义随机的基准点
  100.      * */
  101.     private static int partition3(int[] array, int left, int right) {
  102.         int idx = ThreadLocalRandom.current().nextInt(right-left+1)+left;//生成范围内的随机数
  103.         swap(array,idx,left);//交换随机数与left的值
  104.         int pv = array[left];//基准点的值
  105.         int i = left; //游标i，从最左边开始，找大的
  106.         int j = right; //游标j，从最右边开始，找小的
  107.  
  108.         while (i < j){ //i<j的时候进行循环，一旦i=j或i>j，就要退出循环
  109.             while (i < j && array[j] > pv){//找比基准点小的值，没找到j就--，一旦找到，就退出循环
  110.                 j--;
  111.             }
  112.             while (i<j && array[i]<=pv){//找比基准点大的值，没找到i就++，一旦找到，就退出循环
  113.                 i++;
  114.             }
  115.             swap(array,i,j);//交换
  116.         }
  117.         swap(array,left,i);
  118.         return i;
  119.     }
  120.     /**
  121.      * 改进后的算法
  122.      * 为了处理重复的元素
  123.      * */
  124.     private static int partition4(int[] array, int left, int right) {
  125.         int pv = array[left];//基准点的值
  126.         int i = left+1; //游标i，从left+1开始，找大的
  127.         int j = right; //游标j，从最右边开始，找小的
  128.  
  129.         while (i <= j){ //i<=j的时候进行循环，一旦i>j，就要退出循环,当i=j的时候也要进入循环
  130.             while (i <= j && array[j] > pv){//找比基准点小或等于的值，没找到j就--，一旦找到，就退出循环
  131.                 j--;
  132.             }
  133.             while (i<=j && array[i] < pv){//找比基准点大或相等的值，没找到i就++，一旦找到，就退出循环
  134.                 i++;
  135.             }
  136.             if (i<=j){
  137.                 swap(array,i,j);//交换
  138.                 i++;
  139.                 j--;
  140.             }
  141.         }
  142.         swap(array,left,j);
  143.         return j;
  144.     }
  145. }

应用场景

略

算法分析

最佳情况：T ( n ) = O ( nlogn )

最差情况：T ( n ) = O ( n^2 )

平均情况：T ( n ) = O ( nlogn )

3.插入排序

算法简介

  1. 左边第一个元素可作为有序子数组；
  2. 从第二个元素开始，依次向前比较，大于该元素的则向右移一位，直到比该元素小的元素，插入其后；
  3. 依次向后推进，直至整个数组成为有序数组

动图演示

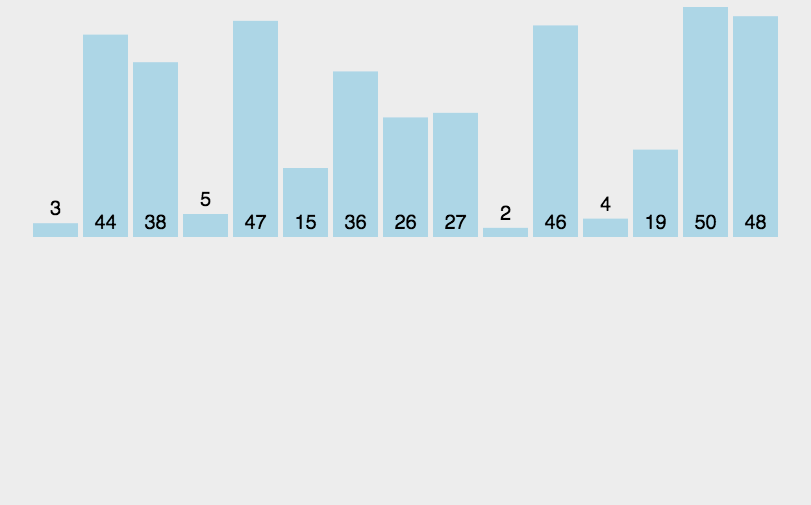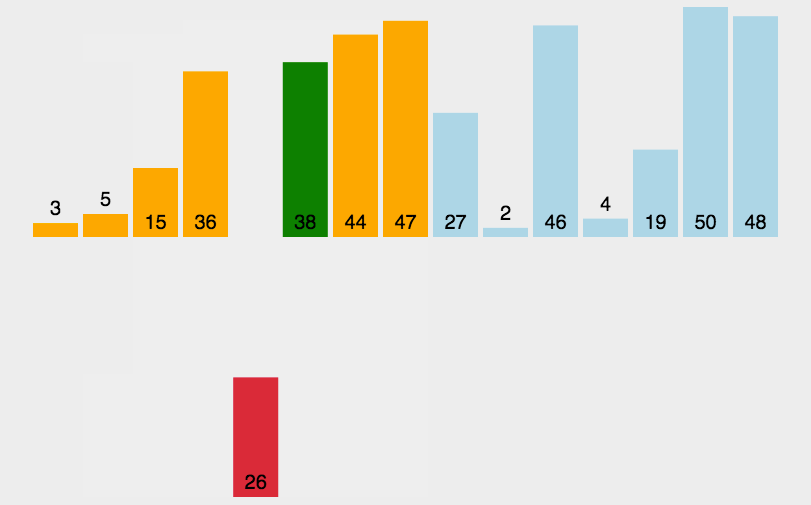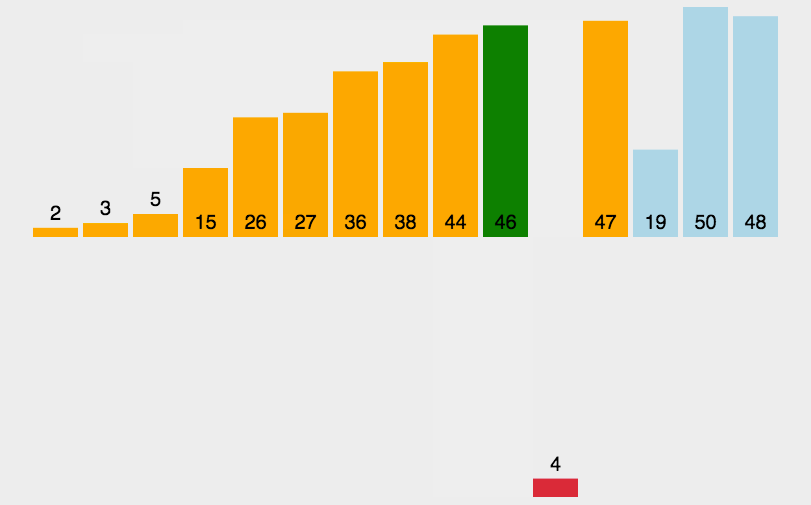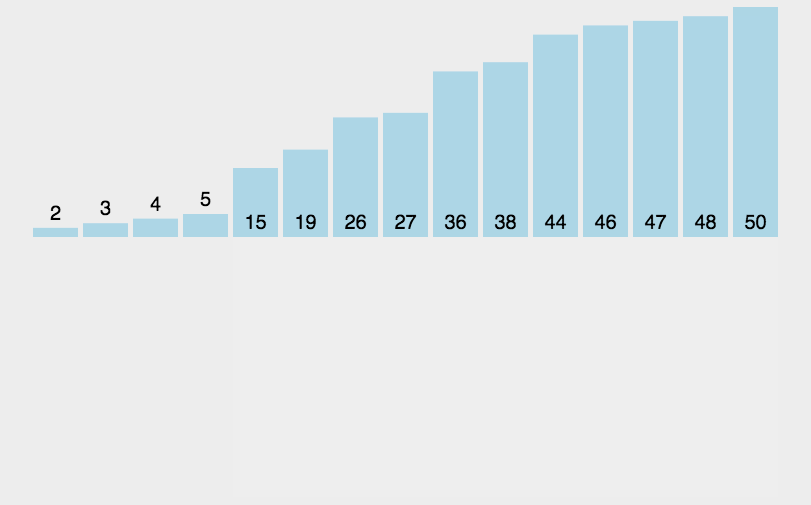
代码演示

  1. package Sorts;
  2.  
  3. import java.util.Arrays;
  4. //插入排序
  5. public class InsertSort {
  6.     public static void main(String[] args) {
  7.         int [] arr = new int[]{5,9,2,7,3,1,10};
  8.         Insert2(arr);
  9.         System.out.println(Arrays.toString(arr));
  10.     }
  11.     //递归版的方法
  12.     public static void Insert1(int[]arr, int low){
  13.         if (low == arr.length)
  14.             return;
  15.         int t = arr[low];
  16.         int i = low-1;
  17.         //从右向左找插入位置，如果比待插入元素大，则不断右移，空出插入位置
  18.         while (i >= 0 && t <arr[i]){
  19.             arr[i+1] = arr[i];
  20.             i--;
  21.         }
  22.         //找到插入位置
  23.         if (i+1 != low){
  24.             arr[i+1] = t;
  25.         }
  26.         Insert1(arr,low+1);
  27.     }
  28.  
  29.     public static void Insert2(int[]arr){
  30.         for (int low = 1; low < arr.length-1 ; low++) {
  31.             int t = arr[low];
  32.             int i = low-1;
  33.             //从右向左找插入位置，如果比待插入元素大，则不断右移，空出插入位置
  34.             while (i >= 0 && t <arr[i]){
  35.                 arr[i+1] = arr[i];
  36.                 i--;
  37.             }
  38.             //找到插入位置
  39.             if (i+1 != low){
  40.                 arr[i+1] = t;
  41.             }
  42.         }
  43.     }
  44. }

应用场景

如果大部分数据距离它正确的位置很近或者近乎有序？例如银行的业务完成的时间
如果是这样的话，插入排序是更好的选择。

算法分析

最佳情况：T ( n ) = O ( n )

最坏情况：T ( n ) = O ( n^2 )

平均情况：T ( n ) = O ( n^2 )

4.选择排序

算法简介

首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

动图演示

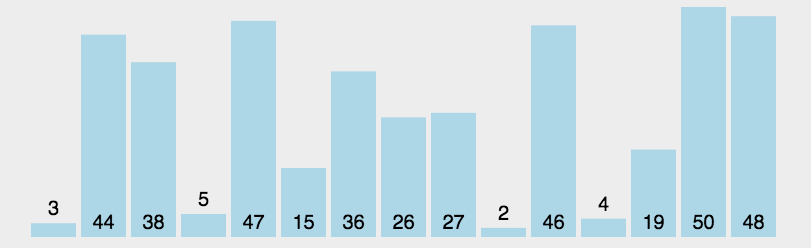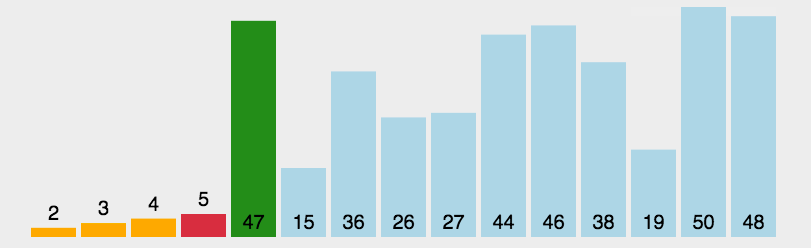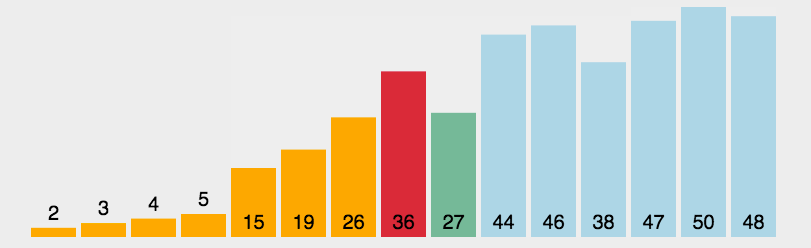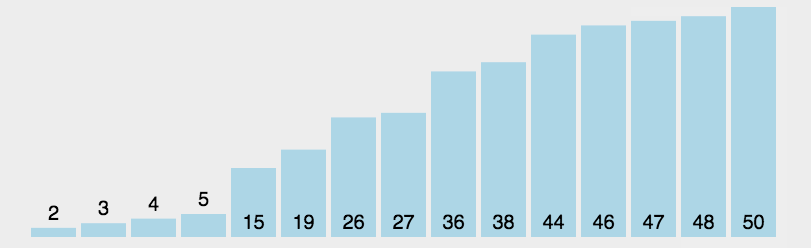
代码演示

  1. package Sorts;
  2.  
  3. import java.util.Arrays;
  4. //选择排序
  5. public class ChooseSort {
  6.     public static void main(String[] args) {
  7.         int [] arr = new int [] {5,9,2,7,3,1,10};
  8.         sort(arr);
  9.         System.out.println(Arrays.toString(arr));
  10.     }
  11.  
  12.     public static void sort(int []arr){
  13.         for (int i = 0; i <arr.length ; i++) {//从第一个索引开始，遍历数组
  14.             for (int j = i; j <arr.length ; j++) {//从当前索引位置开始，遍历后面的数组
  15.                 if (arr[j]<arr[i]){//后面的数组元素比它小，就交换他两的位置（这两元素不相邻）
  16.                     int temp = arr[i];
  17.                     arr[i]=arr[j];
  18.                     arr[j]=temp;
  19.                 }
  20.             }
  21.         }
  22.     }
  23. }

应用场景

当数据量较小的时候适用

算法分析

最佳情况：T ( n ) = O ( n^2 )

最差情况：T ( n ) = O ( n^2 )

平均情况：T ( n ) = O ( n^2 )

5.归并排序

算法简介

分：

  1. 一直分两组，分别对两个数组进行排序（根据上层对下层在一组的数据通过临时数组排序，再将有序数组挪回上层数组中）。
  2.  循环第一步，直到划分出来的“小组”只包含一个元素，只有一个元素的数组默认为已经排好序。

合：（合并时，站在上层合并下层（使组内有序））

  1. 将两个有序的数组合并到一个大的数组中。
  2. 从最小的只包含一个元素的数组开始两两合并。此时，合并好的数组也是有序的。最后把小组合成一个组。

图片演示

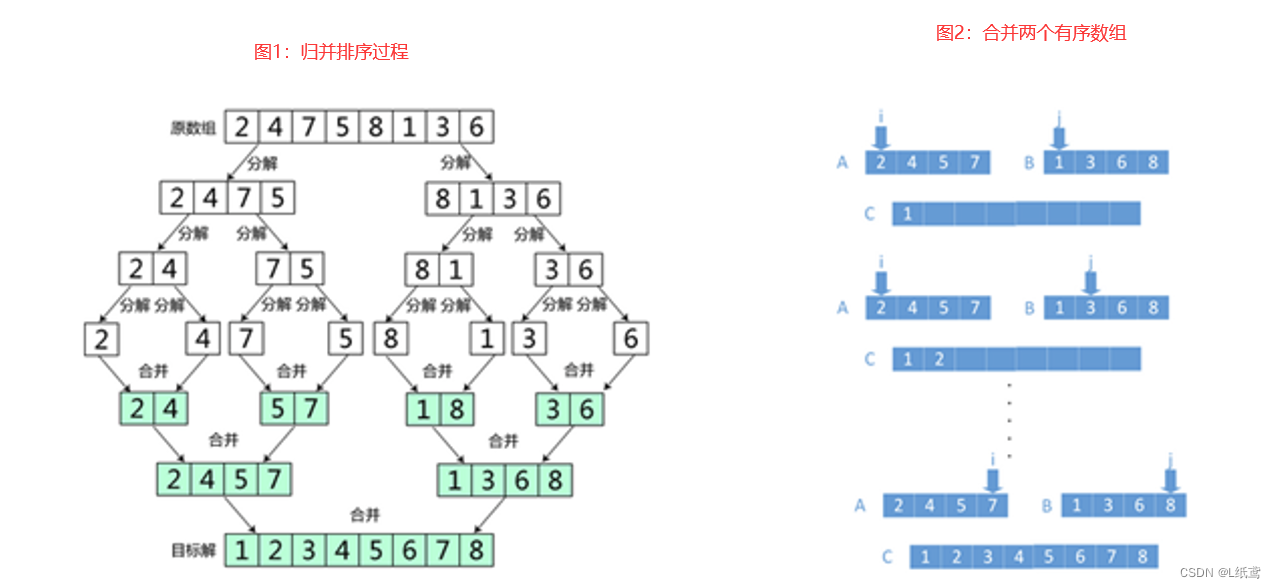
代码演示

  1. package Sorts;
  2.  
  3. import java.util.Arrays;
  4. //归并排序
  5. public class Merge {
  6.     public static void main(String[] args) {
  7.         int[] array = new int[]{13,56,2,8,19,34,29};
  8.         System.out.println("排序前："+ Arrays.toString(array));
  9.         mergeSort(array,0,array.length-1);
  10.         System.out.println("排序后："+Arrays.toString(array));
  11.     }
  12.     public static void mergeSort(int[] array, int low, int height){
  13.         if (low >= height)
  14.             return;
  15.         int mid = (low+height)>>>1;
  16.         mergeSort(array,low,mid);
  17.         mergeSort(array,mid+1,height);
  18.         merge(array,low,mid,height);
  19.     }
  20.     public static void merge(int[] array,int low,int mid,int height){
  21.         int[] ret = new int[height-low+1];
  22.         int i = 0;//新数组的索引
  23.         int s1 = low;//前一个分段的初始位置
  24.         int s2 = mid+1;//后一个分段的初始位置
  25.  
  26.         while (s1<=mid && s2<=height){
  27.             if (array[s1]<=array[s2]){//比较元素的大小
  28.                 ret[i++] = array[s1++];//赋值给新数组，然后索引++
  29.             }else {
  30.                 ret[i] = array[s2];
  31.                 i++;
  32.                 s2++;
  33.             }
  34.         }
  35.         while (s1<=mid){//将前半段剩下的全部赋值到新数组中
  36.             ret[i++] = array[s1++];
  37.         }
  38.         while (s2<=height){//将后半段剩下的全部赋值到新数组中
  39.             ret[i++] = array[s2++];
  40.         }
  41.         for (int j = 0; j < ret.length; j++) {//将新数组中的元素全部挪到原数组中
  42.             array[j+low] = ret[j];
  43.         }
  44.     }
  45. }

应用场景

内存空间不足的时候使用归并排序，能够使用并行计算的时候使用归并排序。

算法分析

最佳情况：T ( n ) = O ( n )

最差情况：T ( n ) = O ( nlogn )

平均情况：T ( n ) = O ( nlogn )

6.希尔排序

算法简介

  1. 首先选择一个步长值gap，以步长值为间隔把数组分为gap个子数组gap=length/2
  2. 对每个子数组进行插入排序；
  3. 逐步减小步长 gap = gap/2,重复对数组进行1，2 步骤；
  4. 当步长值减为1时，相当于对数组进行一次直接插入排序。

图片演示

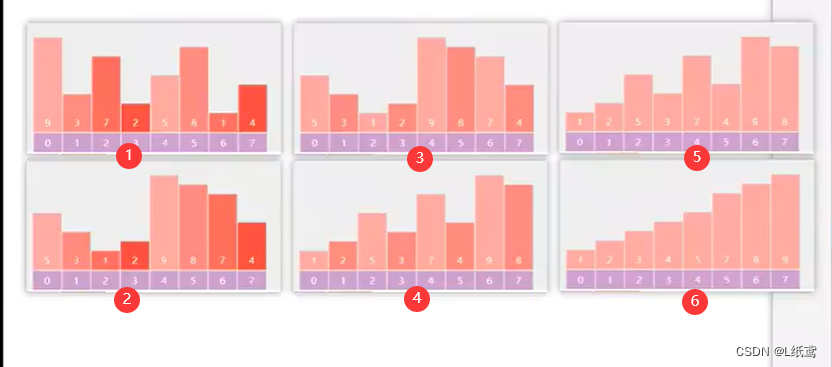
代码演示

  1. package Sorts;
  2.  
  3. import java.util.Arrays;
  4. //希尔排序
  5. public class XiErSort {
  6.     public static void main(String[] args) {
  7.         int [] arr = new int []{5,9,2,7,3,1,10};
  8.         xiEr(arr);
  9.         System.out.println(Arrays.toString(arr));
  10.     }
  11.     public static void xiEr(int arr[]){
  12.         for (int gap = arr.length/2; gap >0 ; gap /=2) {
  13.             for (int low = gap; low <arr.length ; low++) {
  14.                 int t = arr[low];
  15.                 int i = low - gap;
  16.                 //自右向左找插入位置，如果比待插入的元素大，则不断右移，空出插入位置
  17.                 while (i >= 0 && t < arr[i]){
  18.                     arr[i+gap] = arr[i];
  19.                     i-=gap;
  20.                 }
  21.                 //找到插入位置
  22.                 if(i != low-gap){
  23.                     arr[i+gap] = t;
  24.                 }
  25.             }
  26.         }
  27.     }
  28. }

应用场景

相对于直接插入排序，希尔排序要高效很多，因为当gap 值较大时，对子数组进行插入排序时要移动的元素很少，元素移动的距离很大，这样效率很高；在gap逐渐减小过程中，数组中元素已逐渐接近排序的状态，所以需要移动的元素逐渐减少；当gap为1时，相当于进行一次直接插入排序，但是各元素已接近排序状态，需要移动的元素很少且移动的距离都很小。

算法分析

最佳情况：T ( n ) = O ( nlog2 n )

最坏情况：T ( n ) = O ( nlog2 n )

平均情况：T ( n ) = O ( nlog2 n )

7.堆排序

算法简介

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

堆排序可以说是一种利用堆的概念来排序的选择排序。

分为两种方法：

  • 大顶堆：每个节点的值都大于或等于其子节点的值，在堆排序算法中用于升序排列；
  • 小顶堆：每个节点的值都小于或等于其子节点的值，在堆排序算法中用于降序排列；

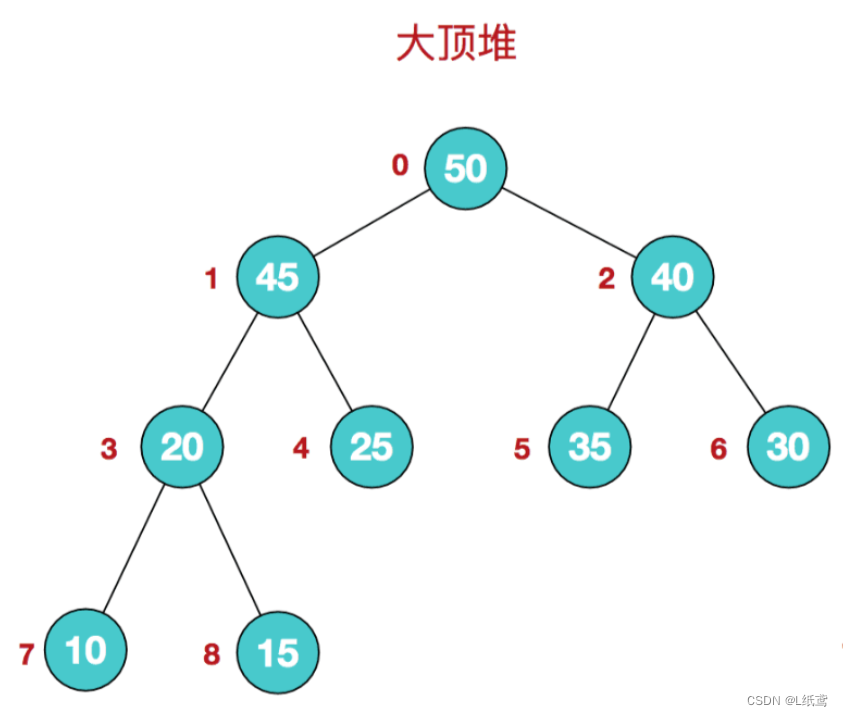
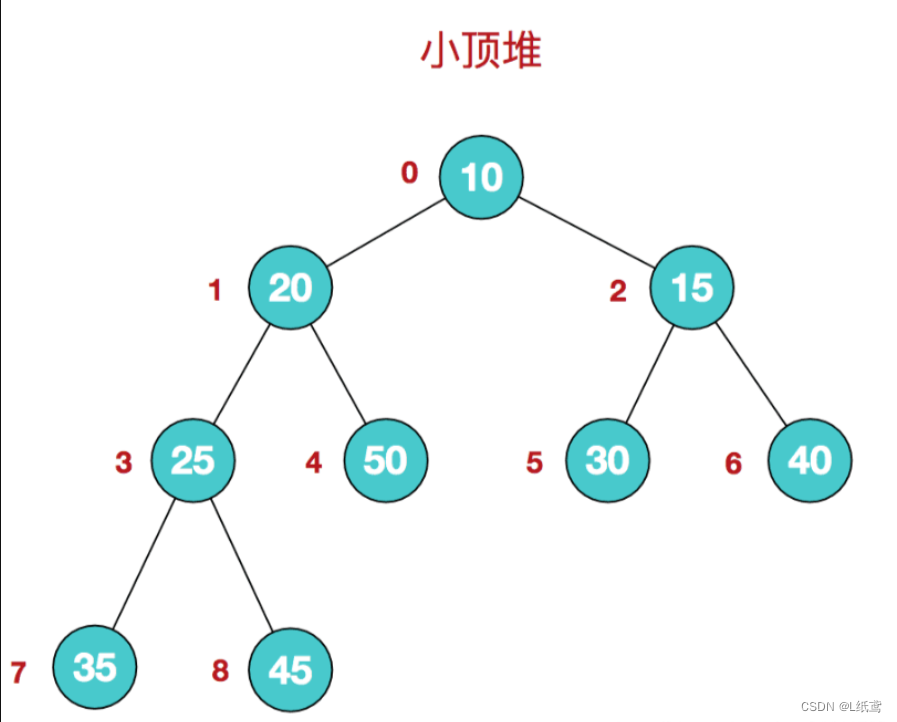
图片演示

步骤一 ：构造初始堆。将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，降序采用小顶堆)。
　　a.假设给定无序序列结构如下

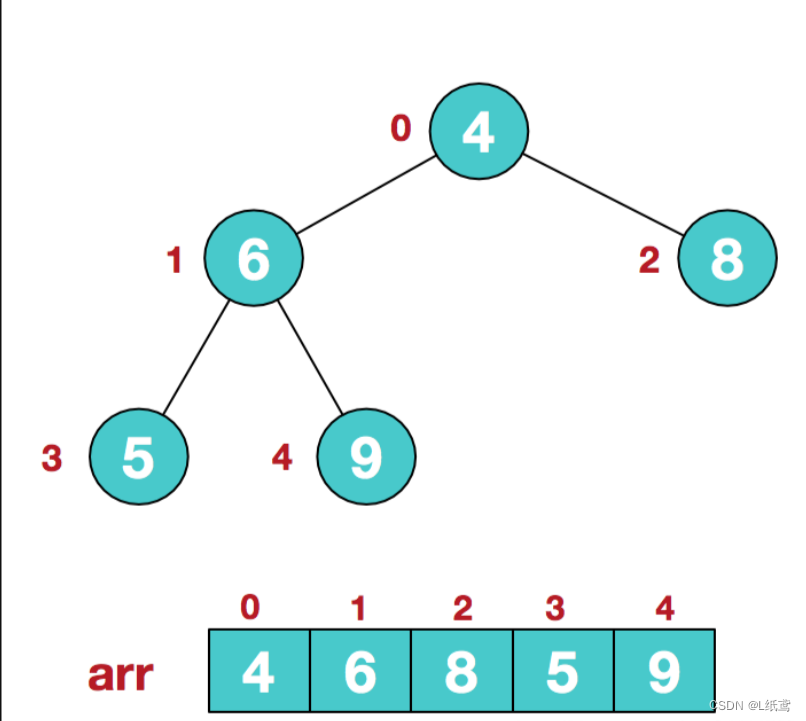
此时我们从最后一个非叶子结点开始（叶结点自然不用调整，第一个非叶子结点 arr.length/2-1=5/2-1=1，也就是下面的6结点），从左至右，从下至上进行调整。

此处必须注意，我们把 6 和 9 比较交换之后，必须考量 9 这个节点对于其子节点会不会产生任何影响？因为其是叶子节点，所以不加考虑；

但是，一定要熟练这种思维，写代码的时候就比较容易理解为什么会出现一次非常重要的交换了。

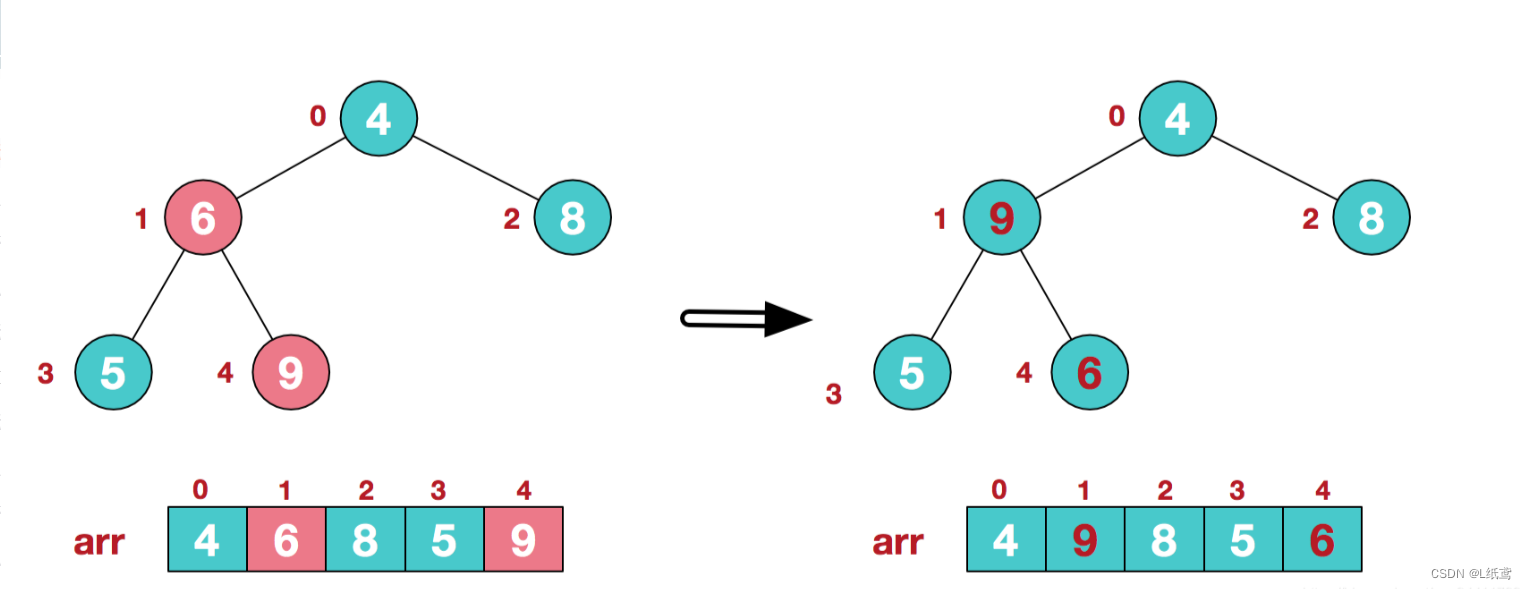
找到第二个非叶节点4，由于[4,9,8]中9元素最大，4和9交换。

在真正代码的实现中，这时候4和9交换过后，必须考虑9所在的这个节点位置，因为其上的值变了，必须判断对其的两个子节点是否造成了影响，这么说不合适，实际上就是判断其作为根节点的那棵子树，是否还满足大根堆的原则，每一次交换，都必须要循环把子树部分判别清楚。

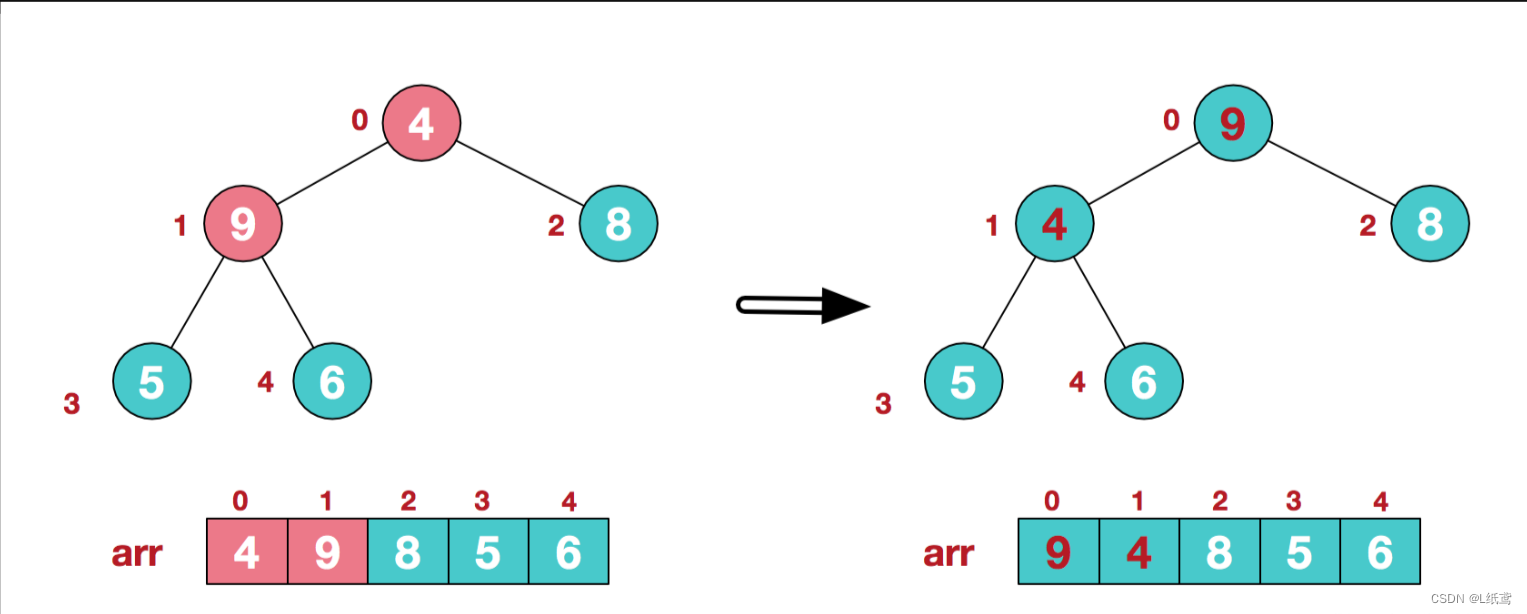
这时，交换导致了子根[4,5,6]结构混乱，继续调整，[4,5,6]中6最大，交换4和6。

牢记上面说的规则，每次交换都要把改变了的那个节点所在的树重新判定一下，这里就用上了，4和9交换了，变动了的那棵子树就必须重新调整，一直调整到符合大根堆的规则为截。

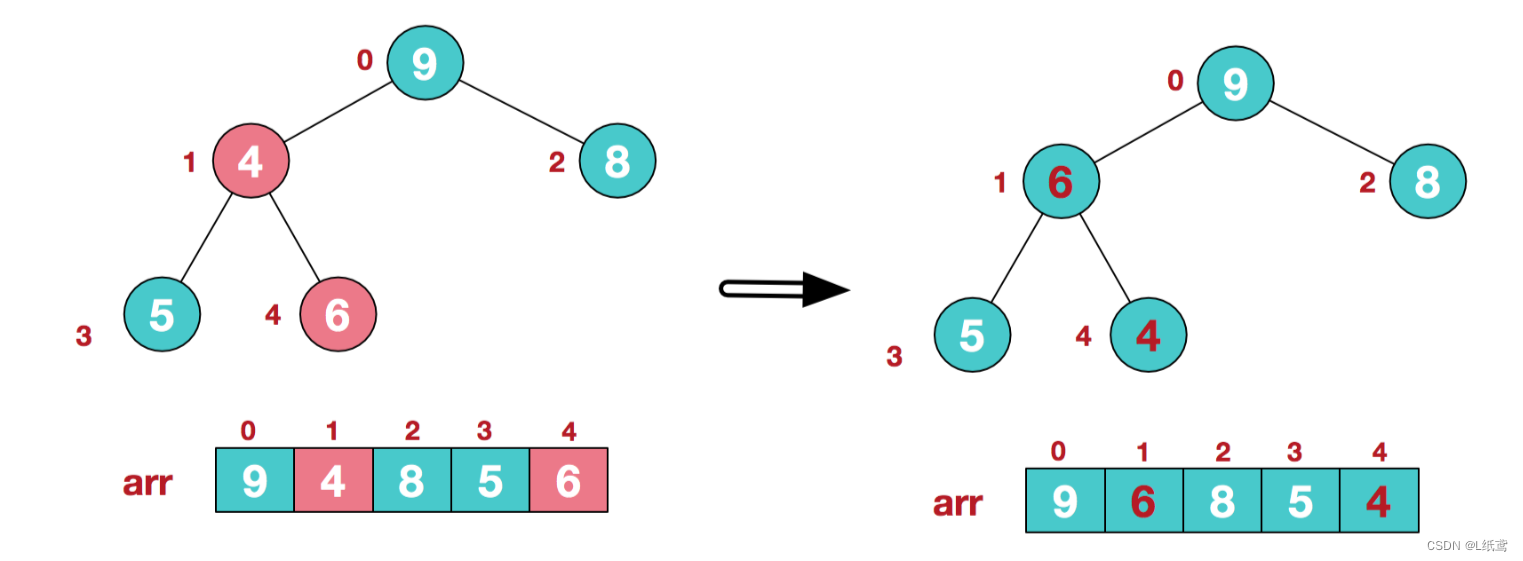
此时，我们就将一个无序序列构造成了一个大顶堆。

步骤二 ：将堆顶元素与末尾元素进行交换，使末尾元素最大。然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换。

将堆顶元素9和末尾元素4进行交换

这里，必须说明一下，所谓的交换，实际上就是把最大值从树里面拿掉了，剩下参与到排序的树，其实只有总结点的个数减去拿掉的节点个数了。所以图中用的是虚线。

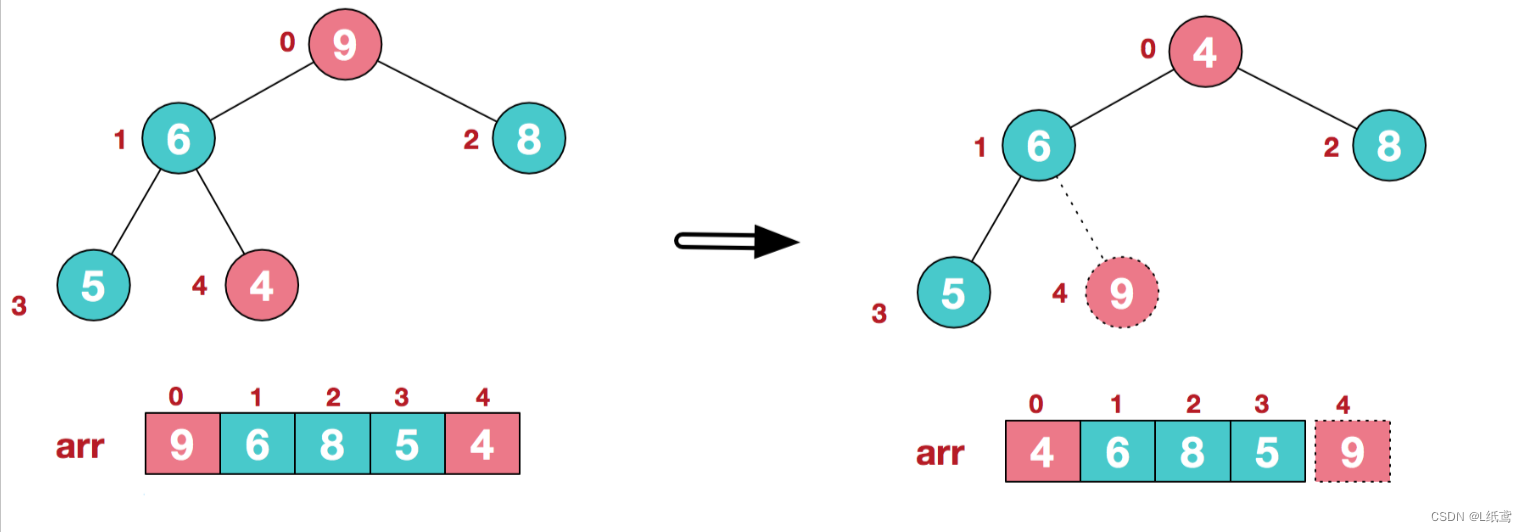
重新调整结构，使其继续满足堆定义

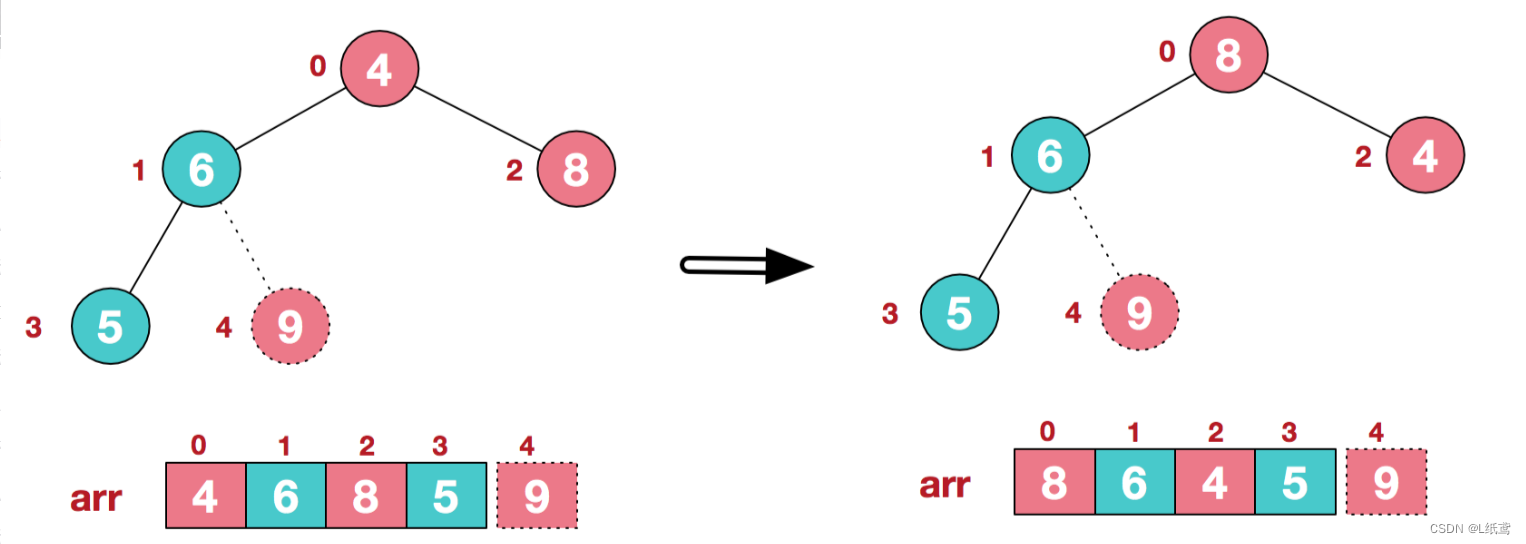
再将堆顶元素8与末尾元素5进行交换，得到第二大元素8.

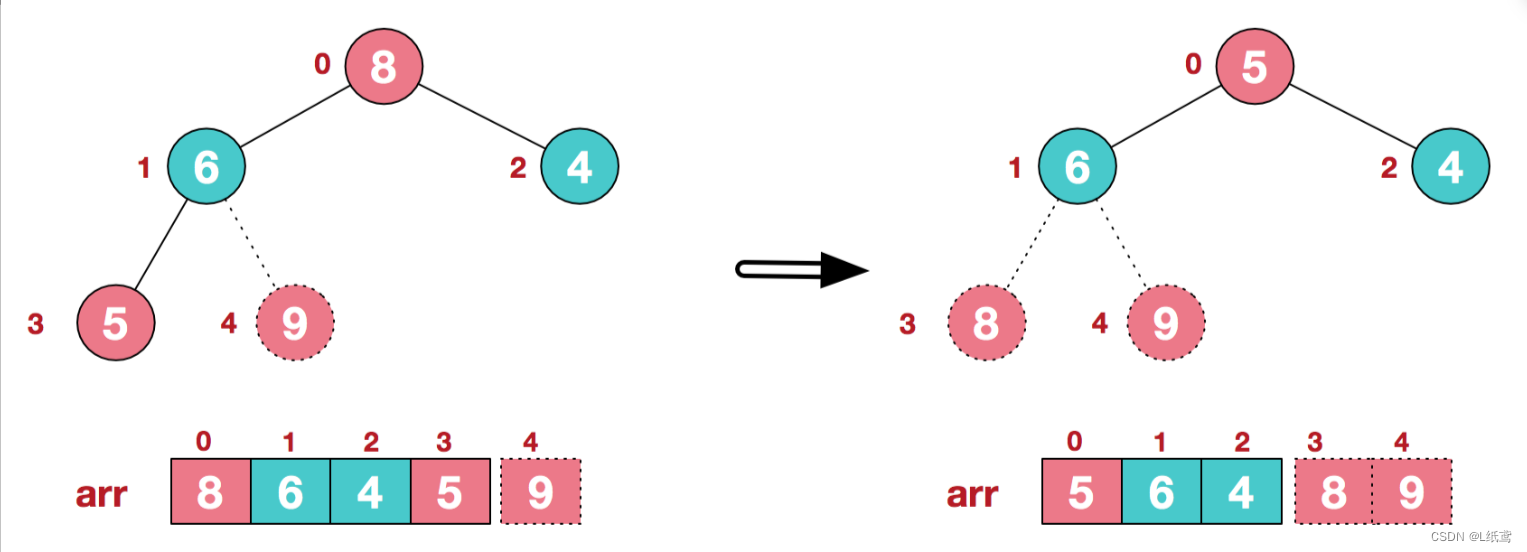
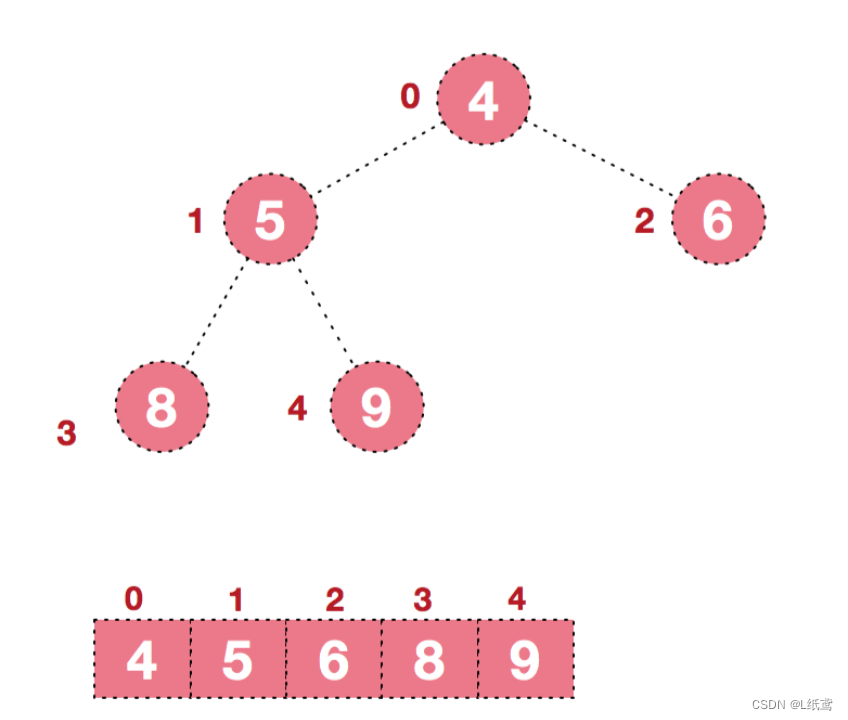
后续过程，继续进行调整，交换，如此反复进行，最终使得整个序列有序

代码演示

  1. package Sorts;
  2. //堆排
  3. public class HeapSort {
  4.     public static void main(String[] args) {
  5.         int[] arr = {16, 7, 3, 20, 17, 8};
  6.         heapSort(arr);
  7.         for (int i : arr) {
  8.             System.out.print(i + " ");
  9.         }
  10.     }
  11.     /**
  12.      * 创建堆
  13.      */
  14.     private static void heapSort(int[] arr) {
  15.         //创建堆
  16.         for (int i = (arr.length - 1) / 2; i >= 0; i--) {
  17.             //从第一个非叶子结点从下至上，从右至左调整结构
  18.             adjustHeap(arr, i, arr.length);
  19.         }
  20.  
  21.         //调整堆结构+交换堆顶元素与末尾元素
  22.         for (int i = arr.length - 1; i > 0; i--) {
  23.             //将堆顶元素与末尾元素进行交换
  24.             int temp = arr[i];
  25.             arr[i] = arr[0];
  26.             arr[0] = temp;
  27.             //重新对堆进行调整
  28.             adjustHeap(arr, 0, i);
  29.         }
  30.     }
  31.     /**
  32.      * 调整堆
  33.      * @param arr 待排序列
  34.      * @param parent 父节点
  35.      * @param length 待排序列尾元素索引
  36.      */
  37.     private static void adjustHeap(int[] arr, int parent, int length) {
  38.         //将temp作为父节点
  39.         int temp = arr[parent];
  40.         //左孩子
  41.         int lChild = 2 * parent + 1;
  42.         while (lChild < length) {
  43.             //右孩子
  44.             int rChild = lChild + 1;
  45.             // 如果有右孩子结点，并且右孩子结点的值大于左孩子结点，则选取右孩子结点
  46.             if (rChild < length && arr[lChild] < arr[rChild]) {
  47.                 lChild++;
  48.             }
  49.             // 如果父结点的值已经大于孩子结点的值，则直接结束
  50.             if (temp >= arr[lChild]) {
  51.                 break;
  52.             }
  53.             // 把孩子结点的值赋给父结点
  54.             arr[parent] = arr[lChild];
  55.             //选取孩子结点的左孩子结点,继续向下筛选
  56.             parent = lChild;
  57.             lChild = 2 * lChild + 1;
  58.         }
  59.         arr[parent] = temp;
  60.     }
  61. }

应用场景

堆排序适合于数据量非常大的场合（百万数据）。
堆排序不需要大量的递归或者多维的暂存数组。这对于数据量非常巨大的序列是合适的。比如超过数百万条记录，因为快速排序，归并排序都使用递归来设计算法，在数据量非常大的时候，可能会发生堆栈溢出错误。
堆排序会将所有的数据建成一个堆，最大的数据在堆顶，然后将堆顶数据和序列的最后一个数据交换。接下来再次重建堆，交换数据，依次下去，就可以排序所有的数据。

算法分析

最佳情况：T ( n ) = O ( nlogn )

最差情况：T ( n ) = O ( nlogn )

平均情况：T ( n ) = O ( nlogn )

8.计数排序

算法分析

找出待排序的数组中最大和最小的元素；
统计数组中每个值为 i 的元素出现的次数，存入数组C的第 i 项；
对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；
反向填充目标数组：将每个元素i放在新数组的第C( i ) 项，每放一个元素就将C( i ) 减去1。

动图演示

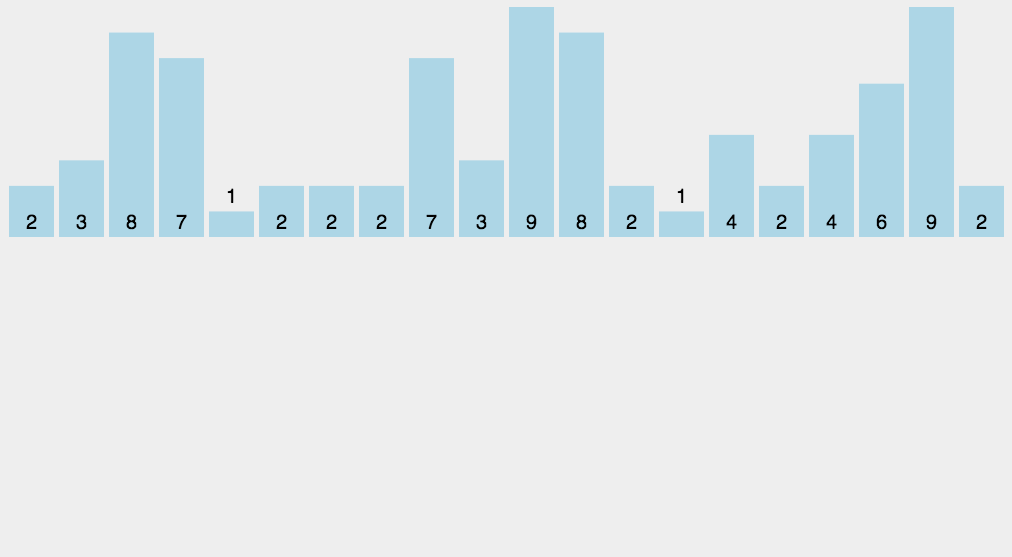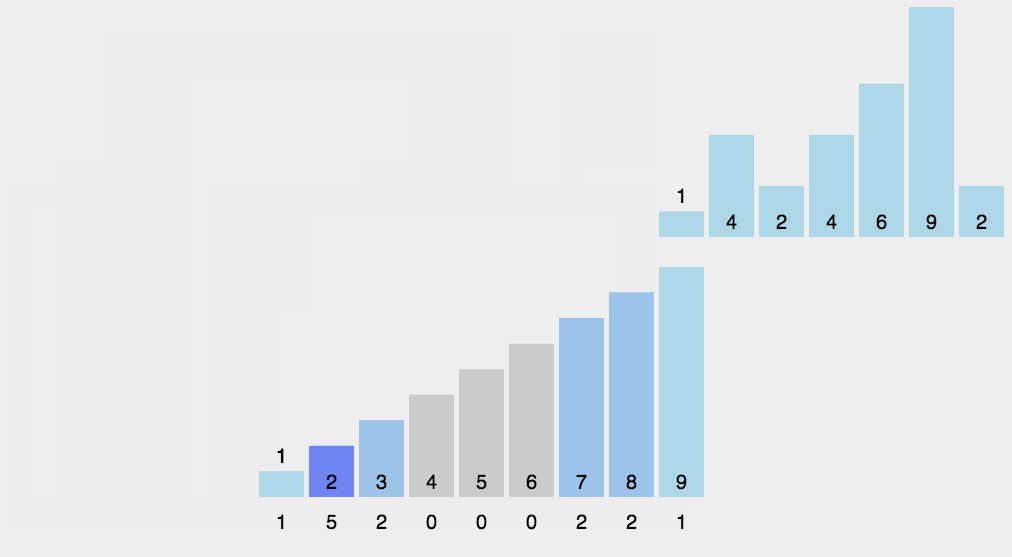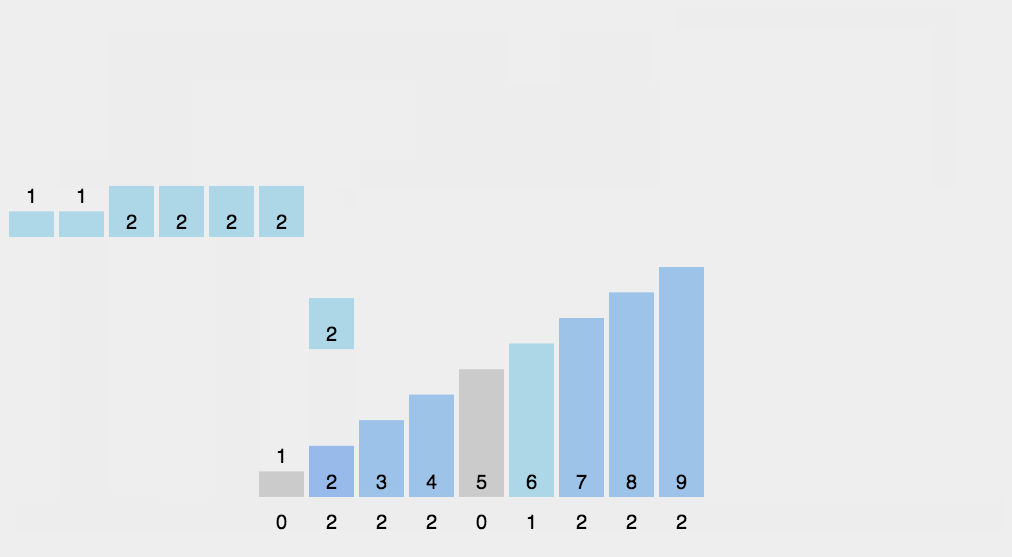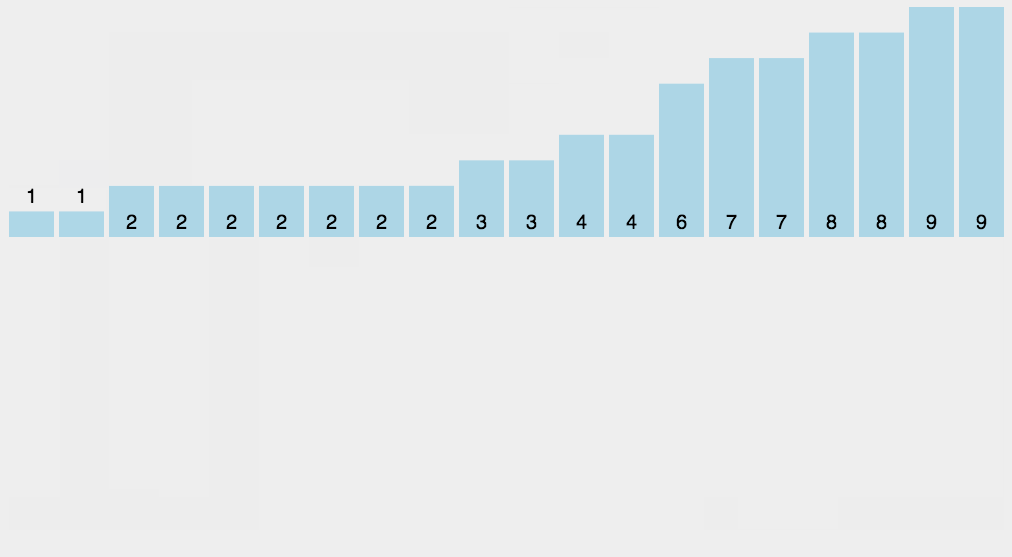
代码演示

  1. package Sorts;
  2.  
  3. import java.util.Arrays;
  4.  
  5. //计数排序
  6. public class CountSort {
  7.     
  8.     public static void main(String[] args) {
  9.         int[] arr = {5,1,1,1,3,0};
  10.         System.out.println(Arrays.toString(arr));
  11.         countSort1(arr);
  12.         System.out.println(Arrays.toString(arr));
  13.     }
  14.  
  15.     //数组中元素>=0
  16.     private static void countSort1(int[] arr) {
  17.         int max = arr[0];
  18.         for (int i = 1; i < arr.length; i++) {
  19.             if (arr[i] > max)
  20.                 max = arr[i];
  21.         }
  22.  
  23.         int[] count = new int[max+1];
  24.  
  25.         for (int v : arr) { //原始数组的元素
  26.             count[v]++;
  27.         }
  28.         int k = 0;
  29.         for (int i = 0; i < count.length; i++) {
  30.             // i 代表原始数组中的元素，count[i]代表出现次数
  31.             while (count[i]>0){
  32.                 arr[k++] = i;
  33.                 count[i]--;
  34.             }
  35.         }
  36.     }
  37.  
  38.     //不限制数组中元素的大小，可以有负数
  39.     private static void countSort2(int[] arr) {
  40.         //让数组中的最小值映射到数组的count[0]位置，最大值映射到count的最右侧
  41.         int min = arr[0];
  42.         int max = arr[0];
  43.         for (int i = 1; i < arr.length; i++) {
  44.             if (arr[i] > max)
  45.                 max = arr[i];
  46.             if (arr[i] < min)
  47.                 min = arr[i];
  48.         }
  49.  
  50.         int[] count = new int[max - min + 1];
  51.  
  52.         //原始数组元素 - 最小值 = count 索引
  53.         for (int v : arr) { //原始数组的元素
  54.             count[v - min]++;
  55.         }
  56.         int k = 0;
  57.         for (int i = 0; i < count.length; i++) {
  58.             // i+min 代表原始数组中的元素，count[i]代表出现次数
  59.             while (count[i]>0){
  60.                 arr[k++] = i + min;
  61.                 count[i]--;
  62.             }
  63.         }
  64.     }
  65. }

应用场景

计数排序需要占用大量空间，它仅适用于数据比较集中的情况。比如 [0，100]，[10000，19999] 这样的数据。

算法分析

最佳情况：T ( n ) = O ( n+k )

最差情况：T ( n ) = O ( n+k )

平均情况：T ( n ) = O ( n+k )

9.基数排序

算法分析

相比其它排序，主要是利用比较和交换，而基数排序则是利用分配和收集两种基本操作。基数排序是一种按记录关键字的各位值逐步进行排序的方法。此种排序一般适用于记录的关键字为整数类型的情况。所有对于字符串和文字排序不适合。

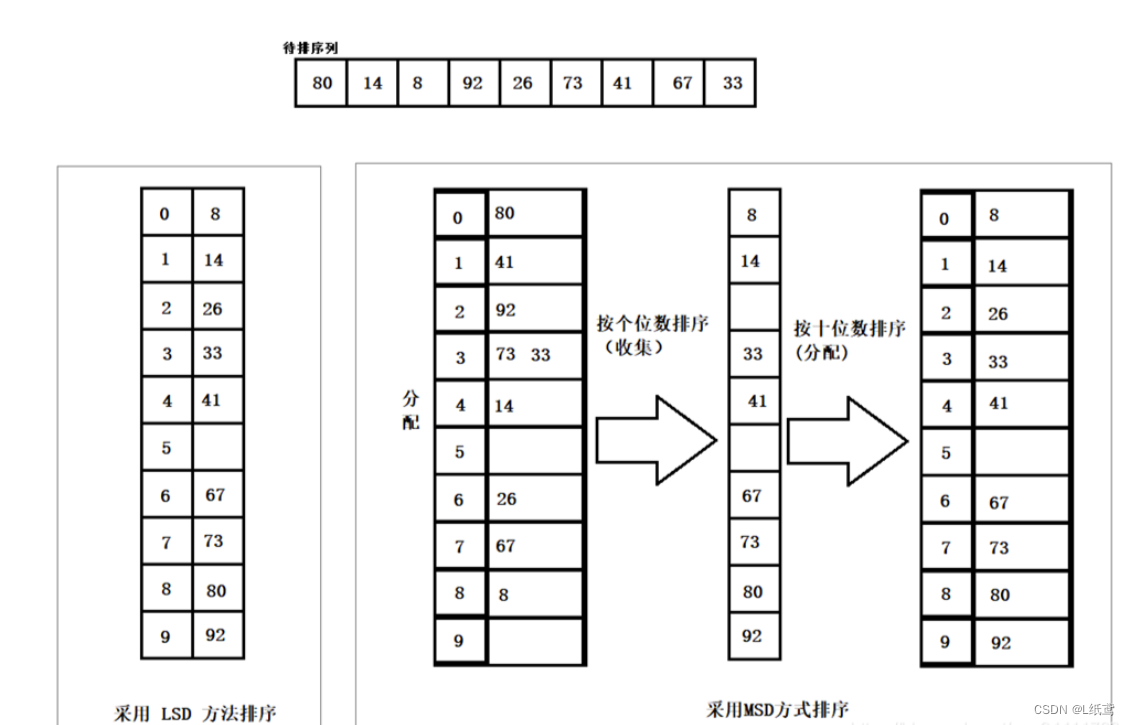
实现：将所有待比较数值（自然数）统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。
基数排序的两种方式：
高位优先，又称为最有效键(MSD),它的比较方向是由右至左；
低位优先，又称为最无效键(LSD),它的比较方向是由左至右；

动图演示

代码演示

  1. package Sorts;
  2.  
  3. import java.util.Arrays;
  4.  
  5. //基数排序
  6. public class RadixSort {
  7.  
  8.     public static void main(String[] args) {
  9.         int [] arr = new int[]{193,255,12,6,78,50,31,564};
  10.         radixSort(arr);;
  11.         System.out.println(Arrays.toString(arr));
  12.  
  13.     }
  14.  
  15.     public static void radixSort(int[] array) {
  16.         if (array == null || array.length <= 1) {
  17.             return;
  18.         }
  19.  
  20.         int length = array.length;
  21.  
  22.         // 每位数字范围0~9，基为10
  23.         int radix = 10;
  24.         int[] aux = new int[length];
  25.         int[] count = new int[radix + 1];
  26.         // 以关键字来排序的轮数，由位数最多的数字决定，其余位数少的数字在比较高位时，自动用0进行比较
  27.         // 将数字转换成字符串，字符串的长度就是数字的位数，字符串最长的那个数字也拥有最多的位数
  28.         int x = Arrays.stream(array).map(s -> String.valueOf(s).length()).max().getAsInt();
  29.  
  30.         // 共需要d轮计数排序, 从d = 0开始，说明是从个位开始比较，符合从右到左的顺序
  31.         for (int d = 0; d < x; d++) {
  32.             // 1. 计算频率，在需要的数组长度上额外加1
  33.             for (int i = 0; i < length; i++) {
  34.                 // 使用加1后的索引，有重复的该位置就自增
  35.                 count[digitAt(array[i], d) + 1]++;
  36.             }
  37.             // 2. 频率 -> 元素的开始索引
  38.             for (int i = 0; i < radix; i++) {
  39.                 count[i + 1] += count[i];
  40.             }
  41.  
  42.             // 3. 元素按照开始索引分类，用到一个和待排数组一样大临时数组存放数据
  43.             for (int i = 0; i < length; i++) {
  44.                 // 填充一个数据后，自增，以便相同的数据可以填到下一个空位
  45.                 aux[count[digitAt(array[i], d)]++] = array[i];
  46.             }
  47.             // 4. 数据回写
  48.             for (int i = 0; i < length; i++) {
  49.                 array[i] = aux[i];
  50.             }
  51.             // 重置count[]，以便下一轮统计使用
  52.             for (int i = 0; i < count.length; i++) {
  53.                 count[i] = 0;
  54.             }
  55.  
  56.         }
  57.     }
  58.  
  59.     //Description: 根据d，获取某个值的个位、十位、百位等，d = 0取出个位，d = 1取出十位，以此类推。对于不存在的高位，用0补
  60.     private static int digitAt(int value, int d) {
  61.         return (value / (int) Math.pow(10, d)) % 10;
  62.     }
  63. }

应用场景

略

算法分析

最佳情况：T ( n ) = O ( n * k )

最差情况：T ( n ) = O ( n * k )

平均情况：T ( n ) = O ( n * k )

10.桶排序

算法分析

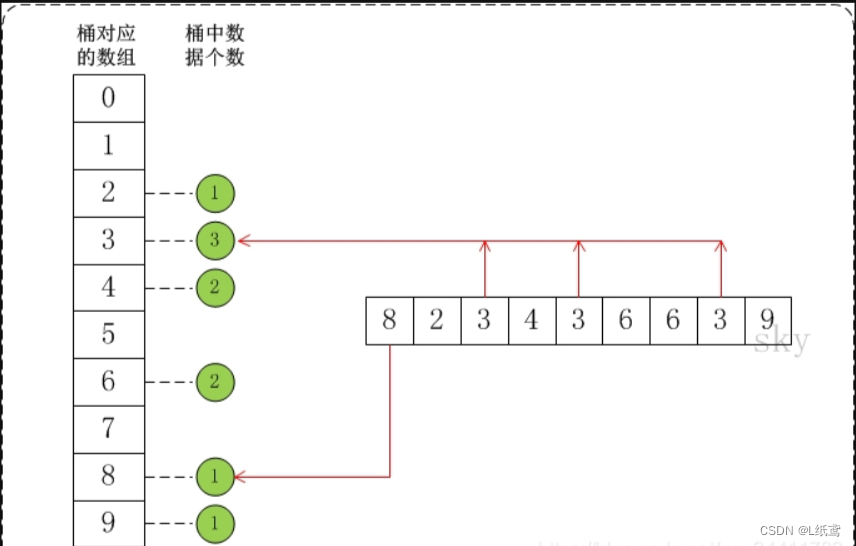
桶排序(Bucket Sort)的原理很简单，它是将数组分到有限数量的桶子里。

假设待排序的数组a中共有N个整数，并且已知数组a中数据的范围[0, MAX)。在桶排序时，创建容量为MAX的桶数组r，并将桶数组元素都初始化为0；将容量为MAX的桶数组中的每一个单元都看作一个"桶"。
在排序时，逐个遍历数组a，将数组a的值，作为"桶数组r"的下标。当a中数据被读取时，就将桶的值加1。例如，读取到数组a[3]=5，则将r[5]的值+1。

动图演示

代码演示

  1. package Sorts;
  2.  
  3. import java.util.*;
  4.  
  5. //桶排
  6. public class BucketSort {
  7.     public static void main(String[] args) {
  8.         int [] arr = new int[]{193,255,12,6,78,50,31,564};
  9.         bucketSort(arr);;
  10.         System.out.println(Arrays.toString(arr));
  11.  
  12.     }
  13.  
  14.     public static void bucketSort(int[] array) {
  15.         if (array == null || array.length <= 1) {
  16.             return;
  17.         }
  18.  
  19.         // 建立桶，个数和待排序数组长度一样
  20.         int length = array.length;
  21.  
  22.         LinkedList<Integer>[] bucket = (LinkedList<Integer>[]) new LinkedList[length];
  23.  
  24.         // 待排序数组中的最大值
  25.         int maxValue = Arrays.stream(array).max().getAsInt();
  26.         // 根据每个元素的值，分配到对应范围的桶中
  27.         for (int i = 0; i < array.length; i++) {
  28.             int index = toBucketIndex(array[i], maxValue, length);
  29.             // 没有桶才建立桶(延时)
  30.             if (bucket[index] == null) {
  31.                 bucket[index] = new LinkedList<>();
  32.             }
  33.             // 有桶直接使用
  34.             bucket[index].add(array[i]);
  35.         }
  36.  
  37.         // 对每个非空的桶排序，排序后顺便存入临时的List，则list中已经有序）
  38.         List<Integer> temp = new ArrayList<>();
  39.         for (int i = 0; i < length; i++) {
  40.             if (bucket[i] != null) {
  41.                 Collections.sort(bucket[i]);
  42.                 temp.addAll(bucket[i]);
  43.             }
  44.         }
  45.  
  46.         // 将temp中的数据写入原数组
  47.         for (int i = 0; i < length; i++) {
  48.             array[i] = temp.get(i);
  49.         }
  50.     }
  51.  
  52.     private static int toBucketIndex(int value, int maxValue, int length) {
  53.         return (value * length) / (maxValue + 1);
  54.     }
  55.  
  56.     /**
  57.      *
  58.     public static void bucketSort(int arr[] ){
  59.         //定义二维数组
  60.         int [][] bucket = new int[10][arr.length];
  61.         //定义记录桶中数据个数的数组
  62.         int [] bucketElement = new int[10];
  64.         for (int i = 0; i <arr.length ; i++) {
  65.             int element = arr[i] % 10;
  66.             bucket[element][bucketElement[element]] = arr[i];
  67.             bucketElement[element]++;
  68.         }
  70.         int index = 0;
  72.         for (int k = 0; k <bucketElement.length ; k++) {
  73.             if (bucketElement[k]!=0){
  74.                 for (int l = 0; l <bucketElement [k] ; l++) {
  75.                     arr[index] = bucket[k][l];
  76.                     index++;
  77.                 }
  78.             }
  79.             bucketElement[k]=0;
  80.         }
  81.     }
  82.      */
  83. }

应用场景

略

算法分析

桶排序最好情况下使用线性时间O(n)，桶排序的时间复杂度，取决与对各个桶之间数据进行排序的时间复杂度，因为其它部分的时间复杂度都为O(n)。很显然，桶划分的越小，各个桶之间的数据越少，排序所用的时间也会越少。但相应的空间消耗就会增大。


最佳情况：T ( n ) = O ( n+k )

最差情况：T ( n ) = O ( n+k )

平均情况：T ( n ) = O ( n^2 )

11.Java自带的排序算法

JDK7-13：

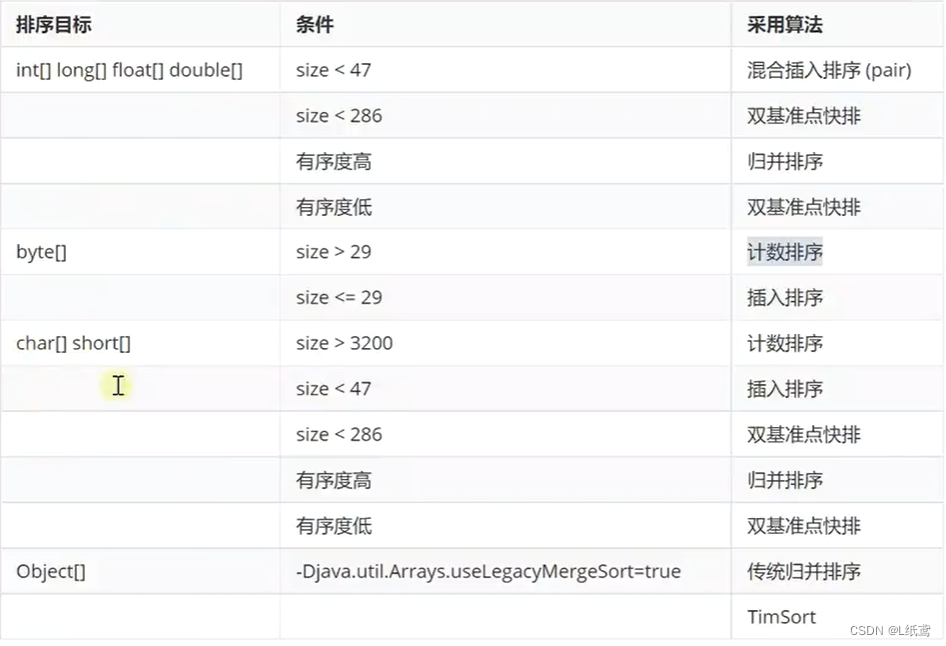
JDK14-20：

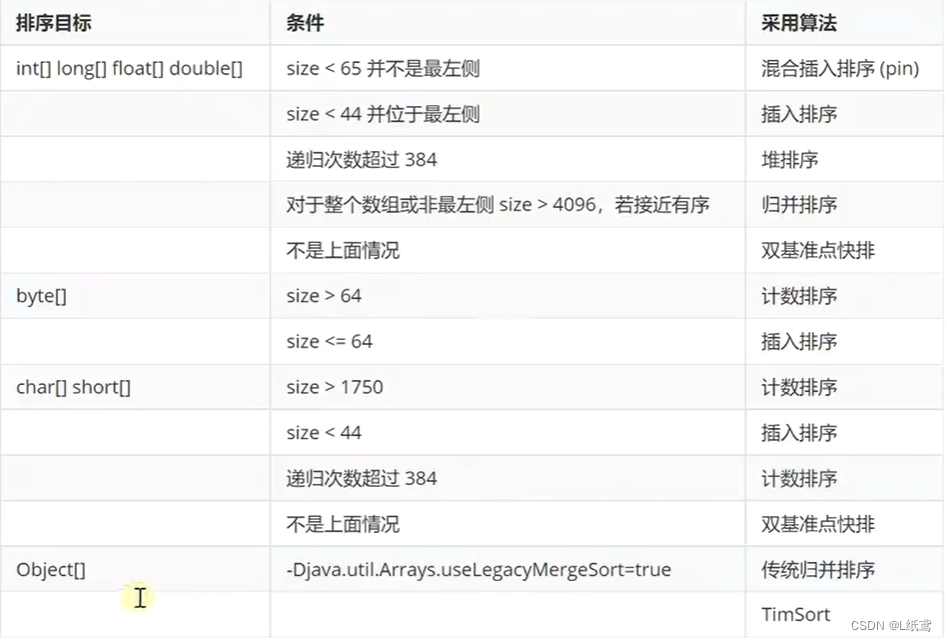
  • 其中TimSort是用归并 + 二分插入排序的混合排序算法
  • 值得注意的是从JDK8开始支持 Arrays.parallelSort 并行排序
  • 根据最新的提交记录来看JDK21可能会引入基数排序等优化

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/花生_TL007/article/detail/438866
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号