对Q-Learning算法的改进：Deep Q-Learning（DQN）_q学习改进

作者：花生_TL007 | 2024-05-16 18:17:22

踩

q学习改进

本篇主要讲述Q-Learning的改进算法,Deep Q-Learning，首先了解一下Q-Learning算法咯

Q-Learning算法

众所周知，Q-Learning是解决强化学习问题的算法。解决强化学习问题用于描述和解决智能体（agent）在与环境的交互过程中通过学习策略以达成回报最大化或实现特定目标的问题。强化学习主要有三个因素：状态，行动和奖励。简单来说主要解决在一个环境下，智能体采取合适的一系列行动来达到最终的目的，每采取一个行动就会得到一定的奖励，有可能是正奖励，也有可能是负奖励（惩罚）。
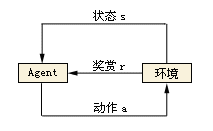
强化学习问题
通过一系列的算法，智能体学习到了策略，可以在现状态下选择合适的行动，最终达到目的。

就说到这里，回到Q-Learning算法：

给定一个状态集S，一个行为集A。s∈S，a∈A。
Q(s,a)是一个值，表示的是s状态下选择行为a的分数，这个Q可以用表格表示。有了这个Q值之后，就可以知道当在状态s的时候，选择那个a了，我们会选择最大Q值的a动作。那么这个Q是怎么来的呢，由奖励得到的。

假如我们给定3个状态s1，s2，s3，s4，假设它们每个只有一个动作分别是a1，a2，a3; s4没有action。在s1状态下进行a1动作(s1,a1)的奖励为r1，执行a1进入到s2，(s2,a2)的奖励为r2，执行a2进入到s3，(s3,a3)的奖励为r3，执行a3进入到s4，无奖励（假设）
强化学习过程图
说明：圆圈代表状态，黑点代表动作。

我们执行s1->a1->s2->a2->s3->a3->s4的过程。这其中Q值该如何计算呢？由奖励R计算。

让我们看下Q(s1,a1)的计算方式：
设 $γ$ 表示衰减因子，0到1之间，根据上面的状态动作过程，我们得到：
$\gamma *r2 + \gamma ^{2}*r3$
可以看出Q(s1,a1)不仅跟现在的状态动作的奖励 $r 1$ 有关，也跟未来的状态动作的奖励 $r 2, r 3$ 有关（不难理解，在现状态下执行的动作，也会影响到未来的状态和动作，所以也跟未来的奖励有关）。

$γ$ 表示现在s1状态选择a1动作跟未来的奖励关系大小的程度。 $γ$ 为0时，说明现在的选择不会影响未来。

同理可以得出：
$\gamma *r3$
$Q (s 3, a 3) = r 3$

我们得到一个规律：
$\gamma *Q(s3,a3)$
$\gamma *(r2 + \gamma *r3)=r1 + \gamma*Q(s2,a2)$
归纳得到公式：
$Q(s_i,a_i)=r_i + \gamma *Q(s_{i+1},a_{i+1})$

好了，现在得到了上诉公式。一个正确的 $Q$ 函数（表格）应该符合上述公式，如果
$r_i + \gamma *Q(s_{i+1},a_{i+1})-Q(s_i,a_i)>0$
说明 $Q$ 小了，加一个正数，那就加 $t$ ， $t$ 就是正数嘛,也就是
$Q(s_i,a_{i}) = Q(s_i,a_{i}) + t$
反之，亦然。
这里的 $t$ 仅仅代表一个方向，加多少，我们在设一个值，步长 $\alpha$ 。
$Q(s_i,a_{i}) = Q(s_i,a_{i}) + \alpha*t$
得到：
$Q(s_i,a_{i}) = Q(s_i,a_{i}) +\alpha ( r_i + \gamma *Q(s_{i+1},a_{i+1})-Q(s_i,a_i))$ 就跟梯度下降没什么两样了。

现在仍然有一个问题，就是一般情况下会出现s会有多个动作选项。
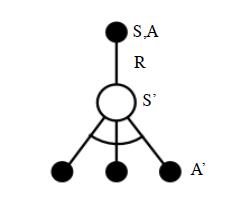
状态对应多个动作

说明：一个状态对应多个动作
其实也不难，我们可以拿出后面状态最大行动的 $Q$ 值就行了。
也就是：

$Q(s_i,a_{i}) = Q(s_i,a_{i}) +\alpha ( r_i + \gamma\max\limits_{a}\ Q(s_{i+1},A)-Q(s_i,a_i))$ $\in A$
好了有了上述公式，基本我们就完成工作了。熟悉机器学习的人都知道还缺样本。
首先我们还得讲解下 $ϵ -$ 贪婪法，它是干什么的，是在现状态选择何种行为a的方法。上面直接选最大值叫贪婪法， $ϵ -$ 贪婪法做了改进，它有一定的机率选择非最大Q值的行为。公式如下：
m表示当前状态可选行为的数量， $ϵ$ 在0-1范围内

$f(a|s)=\left\{$

\begin{aligned} ϵ / m + 1 - ϵ & i f a^{*} = a r g m a x_{a \in A} Q (s, a) \\ ϵ / m & e l s e \end{aligned}

$\begin{aligned} ϵ/m+1−ϵ && if \ \ a^∗=argmax_{a∈A}Q(s,a)\\ ϵ/m && else \end{aligned}$ \right.

f (a ∣ s) = {ϵ / m + 1 - ϵ ϵ / m i f a^{*} = a r g m a x_{a \in A} Q (s, a) e l s e

上述公式表示选择最大

Q

值的a概率为

ϵ / m + 1 - ϵ

，选择其它单个a值为

ϵ / m

。这也符合所以概率相加为1的特性：

(m - 1) * (ϵ / m) + (ϵ / m + 1 - ϵ) = 1

可以看到它不仅仅选最大Q值的a，虽然有最大概率选到a，但是也有一定机率选到其它非最大Q值的a。

现在我们基于状态 $s$ ，用 $ϵ -$ 贪婪法选择到动作 $a$ , 然后执行动作 $a$ ，得到奖励 $r$ ，并进入下一个状态 $s'$ 。这就是训练集了，具体算法如下：

算法输入：迭代轮数 $T$ ，状态集 $S$ , 动作集 $A$ , 步长 $α$ ，衰减因子 $γ$ , 探索率 $ϵ$ ,

输出：所有的状态和动作对应的价值 $Q$

随机初始化所有的状态和动作对应的价值 $Q$ . 对于终止状态其 $Q$ 值初始化为0.
for $i$ from 1 to $T$ ，进行迭代。
a) 初始化 $S$ 为当前状态序列的第一个状态。
b) 用 $ϵ -$ 贪婪法在当前状态 $S$ 选择出动作 $A$
c) 在状态 $S$ 执行当前动作 $A$ ,得到新状态 $S^′$ 和奖励 $R$
d) 更新价值函数 $Q (S, A)$ :
$Q(S,A)=Q(S,A)+α(R+γmax_aQ(S^′,a)−Q(S,A))$ 　
e) $S=S^′$
f) 如果 $S^′$ 是终止状态，当前轮迭代完毕，否则转到步骤b)

算法结束后，得到了 $Q$ 值，每个状态行动时选择最大 $Q$ 值就行了

Deep Q-Learning

Deep Q-Learning算法的基本思路来源于Q-Learning。但是和Q-Learning不同的地方在于，它的Q值的计算不是直接通过状态值s和动作来计算的。上面的Q值是储存在一个表格内，但是如果状态动作数很多时，空间消耗太大。所以我们用网络代替这个Q表，也就是Q网络。

Q网络
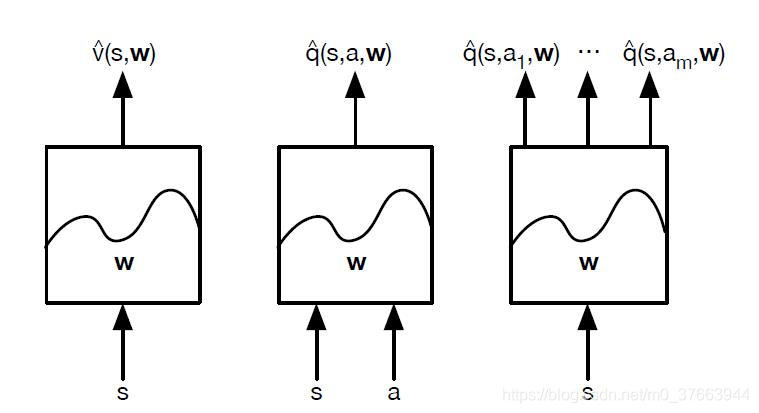
中间和右边那两幅图就是我们这里的Q网络形式。Q网络的形式多种多样，我们这里就简单使用前馈，当然也可以使用cnn。
这里还需要提到一个概念，那就是经验回放集合，也就是数据集合，上面Q-Learning算法我们是一条一条的训练，不需要经验回放集合，这里的神经网络需要batch训练，所以需要它。

那么让我们看下具体的算法：

算法输入：迭代轮数 $T$ ，状态特征维度 $n$ , 动作集 $A$ , 步长 $α$ ，衰减因子 $γ$ , 探索率 $ϵ$ , $Q$ 网络结构, 批量梯度下降的样本数 $m$ 。
输出： $Q$ 网络参数

随机初始化 $Q$ 网络的所有参数 $w$ ，基于 $w$ 初始化所有的状态和动作对应的价值 $Q$ 。清空经验回放的集合 $D$ 。
for $i$ from 1 to $T$ ，进行迭代。
$a)$ 初始化 $S$ 为当前状态序列的第一个状态, 拿到其特征向量 $ϕ (S)$
$b)$ 在 $Q$ 网络中使用 $ϕ (S)$ 作为输入，得到 $Q$ 网络的所有动作对应的 $Q$ 值输出。用 $ϵ -$ 贪婪法在当前 $Q$ 值输出中选择对应的动作 $A$
$c)$ 在状态 $S$ 执行当前动作A,得到新状态 $S^′$ 对应的特征向量 $ϕ(S^′)$ 和奖励 $R$ ,是否终止状态 $is\_end$ ，没有下一个状态
$d)$ 将 ${ϕ(S),A,R,ϕ(S^′),is\_end}$ 这个五元组存入经验回放集合D
$e) S=S^′$
$f)$ 从经验回放集合 $D$ 中采样 $m$ 个样本 ${ϕ(S_j),A_j,R_j,ϕ(S^′_j),is\_end_j},j=1,2.,,,m$ 计算当前目标 $Q$ 值 $y_j$ ：
$\begin{aligned} R_{j} & i s_e n d_{j} i s t r u e \\ R_{j} + γ m a x_{a^{'}} Q (ϕ (S_{j}^{'}), A_{j}^{'}, w) & i s_e n d_{j} i s f a l s e \end{aligned}$
g) 使用均方差损失函数 $\frac{1}{m}∑\limits_{j=1}^m=\frac{1}{m}(y_j−Q(ϕ(S_j),A_j,w))^2$ ，通过神经网络的梯度反向传播来更新 $Q$ 网络的所有参数 $w$
　h) 如果S′是终止状态，当前轮迭代完毕，否则转到步骤b)

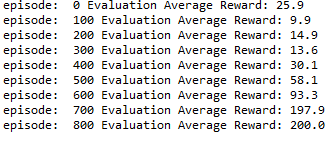
以上就是DQN算法，下面是代码实现，这里使用了OpenAI Gym中的CartPole-v0游戏来作为我们算法应用。CartPole-v0游戏的介绍参见网址。它比较简单，基本要求就是控制下面的cart移动使连接在上面的pole保持垂直不倒。这个任务只有两个离散动作，要么向左用力，要么向右用力。而state状态就是这个cart的位置和速度， pole的角度和角速度，4维的特征。坚持到200分的奖励则为过关。
需要下载gym，以下是pytorch代码实现DQN:

# -*- coding: utf-8 -*-
"""
Created on Mon Dec  2 13:18:25 2019

@author: asus
"""

import gym
import torch
from  collections import deque
import torch.nn.functional as F
import numpy as np
import random
from torch.autograd import Variable


GAMMA = 0.9
INITIAL_EPSILON = 0.5
FINAL_EPSILON = 0.01
REPLAY_SIZE = 10000
BATCH_SIZE = 32
ENV_NAME = 'CartPole-v0'
EPISODE = 3000 # Episode limitation
STEP = 300 # Step limitation in an episode
TEST = 10 # The number of experiment test every 100 episode

class MODEL(torch.nn.Module):
    def __init__(self, env):
        super(MODEL, self).__init__()
        self.state_dim = env.observation_space.shape[0]
        self.action_dim = env.action_space.n
        self.fc1 = torch.nn.Linear(self.state_dim, 20)
        self.fc1.weight.data.normal_(0, 1)
        self.fc2 = torch.nn.Linear(20, self.action_dim)
        self.fc2.weight.data.normal_(0, 0.2)
    
    def create_Q_network(self, x):
        x = F.relu(self.fc1(x))
        Q_value = self.fc2(x)
        return Q_value
    
    def forward(self, x, action_input):
        Q_value = self.create_Q_network(x)
        Q_action = torch.mul(Q_value, action_input).sum(dim=1)
        return Q_action
    
class DQN():
    def __init__(self, env):
        self.Q_net = MODEL(env)
        self.replay_buffer = deque()
        self.time_step = 0
        self.epsilon = INITIAL_EPSILON
        self.optimizer = torch.optim.Adam(params=self.Q_net.parameters(), lr=0.0001)
        self.loss = torch.nn.MSELoss()
        
    def perceive(self,state,action,reward,next_state,done):
        one_hot_action = np.zeros(self.Q_net.action_dim)
        one_hot_action[action] = 1
        self.replay_buffer.append((state,one_hot_action,reward,next_state,done))
        if len(self.replay_buffer) > REPLAY_SIZE:
            self.replay_buffer.popleft()
        if len(self.replay_buffer) > BATCH_SIZE:
            self.train_Q_network()
    
    def train_Q_network(self):
        self.time_step += 1
        # Step 1: obtain random minibatch from replay memory
        minibatch = random.sample(self.replay_buffer,BATCH_SIZE)
        state_batch = [data[0] for data in minibatch]
        action_batch = [data[1] for data in minibatch]
        reward_batch = [data[2] for data in minibatch]
        next_state_batch = torch.FloatTensor([data[3] for data in minibatch])

        # Step 2: calculate y
        y_batch = []
        
        Q_value_batch = self.Q_net.create_Q_network(next_state_batch)
        
        for i in range(0,BATCH_SIZE):
            done = minibatch[i][4]
            if done:
                y_batch.append(reward_batch[i])
            else:
                y_batch.append(reward_batch[i] + GAMMA * torch.max(Q_value_batch[i]))
                
        y = self.Q_net(torch.FloatTensor(state_batch), torch.FloatTensor(action_batch))
        y_batch = torch.FloatTensor(y_batch)
        cost = self.loss(y, y_batch)
        self.optimizer.zero_grad()
        cost.backward()
        self.optimizer.step()
            
    def egreedy_action(self,state):
        Q_value = self.Q_net.create_Q_network(torch.FloatTensor(state))
        if random.random() <= self.epsilon:
            self.epsilon -= (INITIAL_EPSILON - FINAL_EPSILON) / 10000
            return random.randint(0, self.Q_net.action_dim - 1)
        else:
            self.epsilon -= (INITIAL_EPSILON - FINAL_EPSILON) / 10000
            return torch.argmax(Q_value).item()     
                
    def action(self,state):
        return torch.argmax(self.Q_net.create_Q_network(torch.FloatTensor(state))).item()               

def main():
  # initialize OpenAI Gym env and dqn agent
  env = gym.make(ENV_NAME)
  agent = DQN(env)

  for episode in range(EPISODE):
    # initialize task
    state = env.reset()
    # Train
    for step in range(STEP):
      action = agent.egreedy_action(state) # e-greedy action for train
      next_state,reward,done,_ = env.step(action)
      # Define reward for agent
      reward = -1 if done else 0.1
      agent.perceive(state,action,reward,next_state,done)
      state = next_state
      if done:
        break
    # Test every 100 episodes
    if episode % 100== 0:
      total_reward = 0
      for i in range(TEST):
        state = env.reset()
        for j in range(STEP):
          env.render()
          action = agent.action(state) # direct action for test
          state,reward,done,_ = env.step(action)
          total_reward += reward
          if done:
            break
      ave_reward = total_reward/TEST
      print ('episode: ',episode,'Evaluation Average Reward:',ave_reward)

if __name__ == '__main__':
  main()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139

如果需要tensorflow的代码看这里
效果如下：

觉得可以,点个赞,好不啦
参考文献：https://www.cnblogs.com/pinard/p/9714655.html

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/花生_TL007/article/detail/579978