双目相机标定与三维重建_双目标定的意义

1.相机标定的目的：

 （1）通过单目相机标定分别求出左右相机的内参数和外参数。

（2）矫正由于镜头畸变造成的图片的变形，例如，现实中的直线，拍摄成图像后会外凸或内凹，进行相机标定后可以对这种情况进行校正；

（3）利用分别对左右相机标定得到的参数进行双目标定，通过计算得到深度和位置信息，从而进行三维重建和测距等。 

2.四个坐标系

        相机标定的目的之一是为了建立物体从三维世界到成像平面上各坐标点的对应关系，所以首先要了解以下四个坐标系：

世界坐标系：用户定义的三维世界的坐标系，为了描述目标物在真实世界里的位置以及相机所在的位置而被引入。

相机坐标系：在相机上建立的坐标系，为了从相机的角度描述物体位置而定义，作为沟通世界坐标系和图像/像素坐标系的中间一环。

图像坐标系：为了描述成像过程中物体从相机坐标系到图像坐标系的投影透射关系而引入，方便进一步得到像素坐标系下的坐标。

像素坐标系：为了描述物体成像后的像点在数字图像上（相片）的坐标而引入，是我们真正从相机内读取到的信息所在的坐标系，单位为个（像素数目）。

3.坐标之间的转换

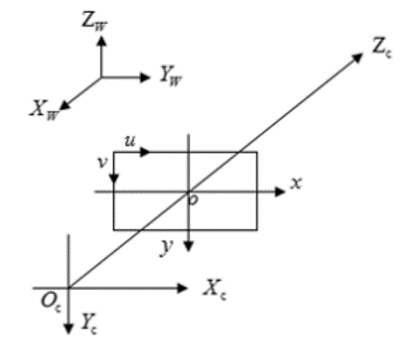
世界坐标系：Xw、Yw、Zw。

相机坐标系： Xc、Yc、Zc。

图像坐标系：x、y。

像素坐标系：u、v。

        其中，相机坐标系的Z轴与光轴重合，且垂直于图像坐标系平面并通过图像坐标系的原点，相机坐标系与图像坐标系之间的距离为焦距f。像素坐标系平面u-v和图像坐标系平面x-y重合，但像素坐标系原点位于图中左上角。

3.1世界坐标系到相机坐标系

假设绕x轴旋转（逆时针）

以此类推，绕其它轴旋转（顺时针）

世界坐标系到相机坐标系要6个自由度，除了旋转还要进行平移

3.2相机坐标系转图像坐标系

3.3图像坐标系转像素坐标系

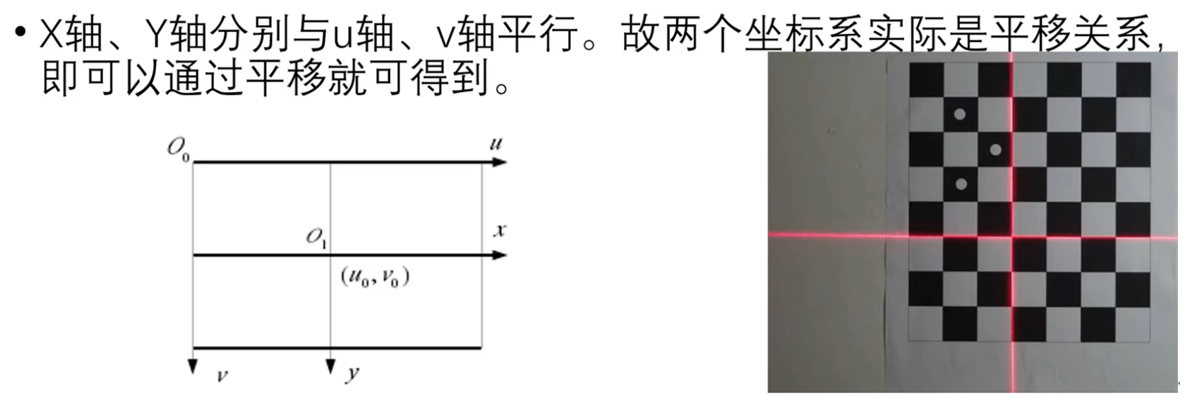
图像坐标系的原点在图像的中央，单位mm。

像素坐标系的原点在图像的左上角，单位是像素Pixel（个）。

dx,dy:是传感器固有的参数，代表每个像素的毫米数。

u0,v0：代表图像坐标系原点相对于像素坐标系的偏移量，单位是像素。

3.4 世界坐标系到像素坐标系转换的全过程

 至此，要想通过拍摄到的二维图像重建三维场景，那么就要求得内参M1和外参M2。

 3.5张正友标定法

 

 

 

单应性（Homography）变换。可以简单的理解为它用来描述物体在世界坐标系和像素坐标系之间的位置映射关系。对应的变换矩阵称为单应性矩阵。

 

 

 

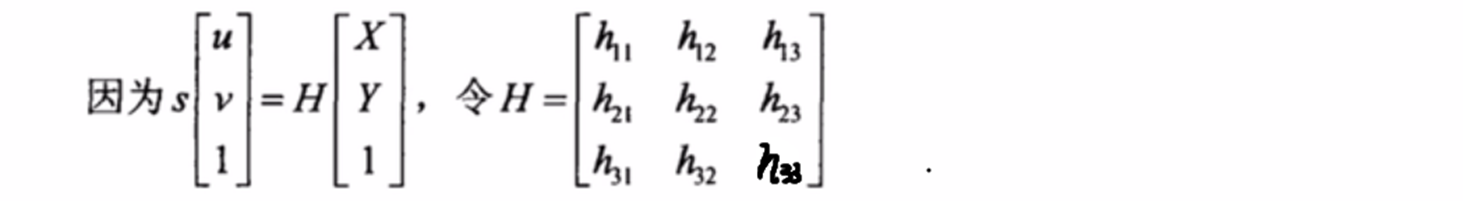
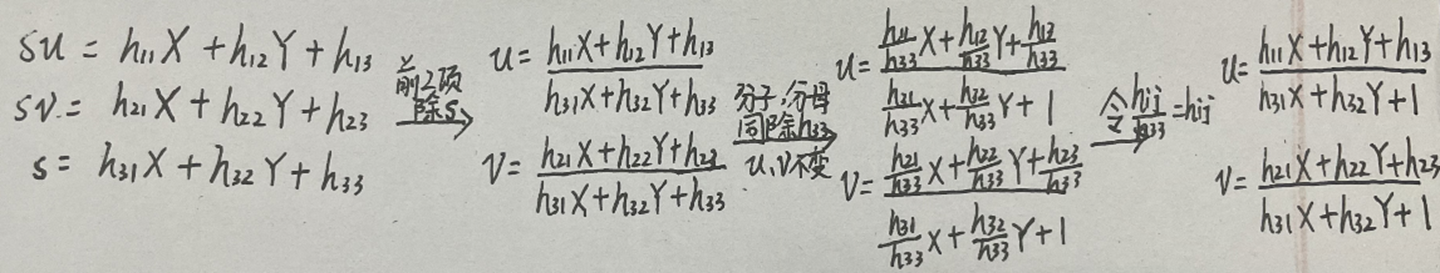
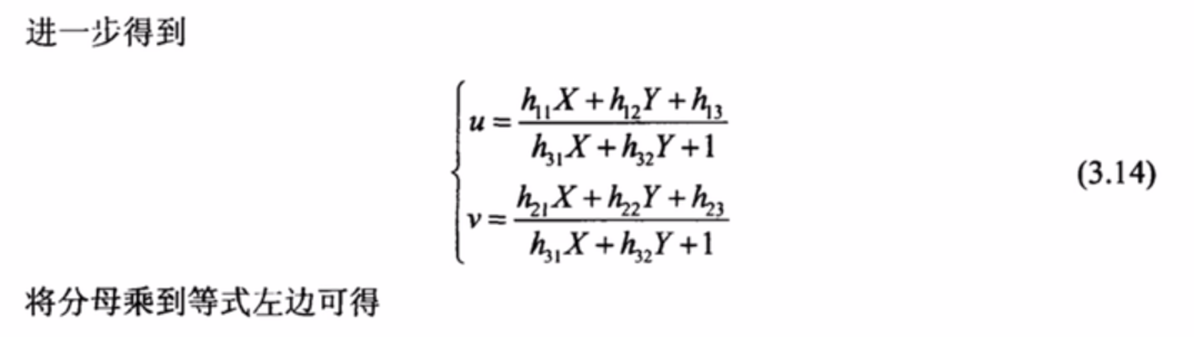
如何根据标定图得到单应矩阵？

经过前面一系列的介绍，我们应该大致明白如何根据打印的棋盘标定图和拍摄的照片来计算单应矩阵H。我们来总结一下大致过程。

1. 打印一张棋盘格标定图纸，将其贴在平面物体的表面。

2. 拍摄一组不同方向棋盘格的图片，可以通过移动相机来实现，也可以移动标定图片来实现。

3. 对于每张拍摄的棋盘图片，检测图片中所有棋盘格的特征点（角点，也就是下图中黑白棋盘交叉点，中间品红色的圆圈内就是一个角点，四个对角（红黄蓝绿）是最特别的角点）。我们定义打印的棋盘图纸位于世界坐标系Zw=0的平面上，世界坐标系的原点位于左图棋盘图纸的固定一角（比如下图中黄色点）。像素坐标系原点位于右图图片左上角。

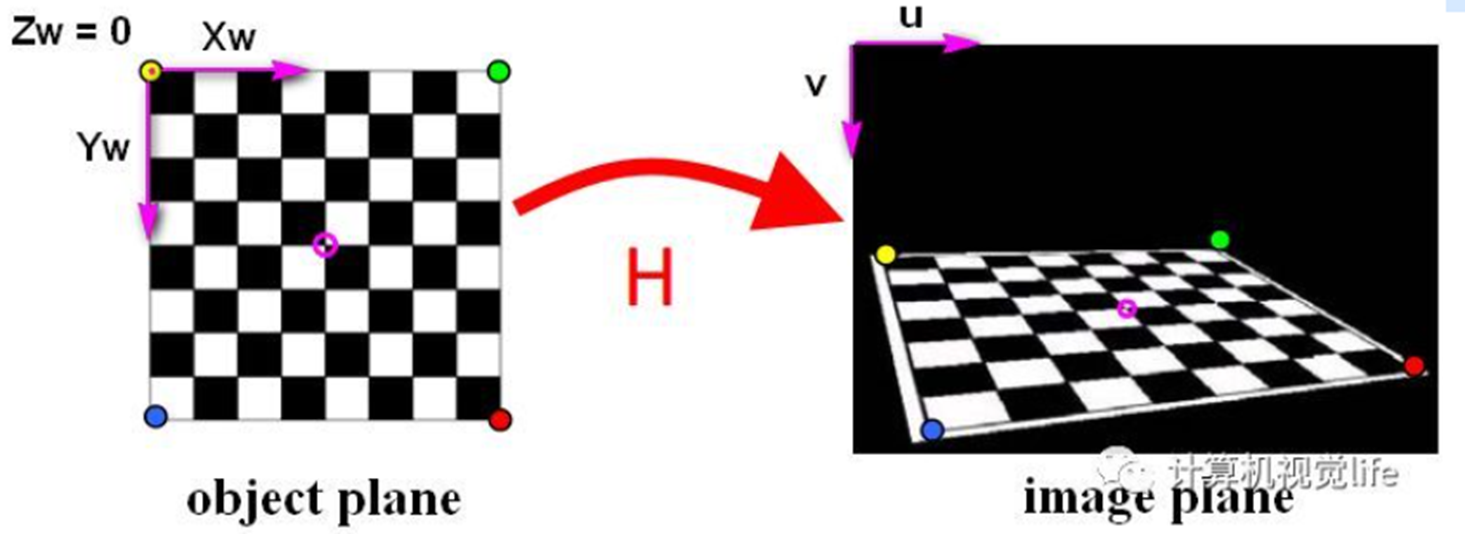
因为棋盘标定图纸中所有角点的空间坐标是已知的，这些角点对应在拍摄的标定图片中的角点的像素坐标也是已知的，如果我们得到这样的N>=4个匹配点对（越多计算结果越鲁棒），就可以根据LM等优化方法得到这个视角下的单应矩阵H。当然计算单应矩阵一般不需要自己写函数实现，OpenCV中就有现成的函数可以调用。

但是，以上只是理论推导，在真实的应用场景中，我们计算的点对中都会包含噪声。比如点的位置偏差几个像素，甚至出现特征点对误匹配的现象，如果只使用4个点对来计算单应矩阵，那会出现很大的误差。因此，为了使得计算更精确，一般都会使用远大于4个点对来计算单应矩阵。另外上述方程组采用直接线性解法通常很难得到最优解，所以实际使用中一般会用其他优化方法，如奇异值分解、Levenberg-Marquarat（LM）算法

通过以上方法求得的单应性矩阵H后，以下是通过H反推相机的内外参

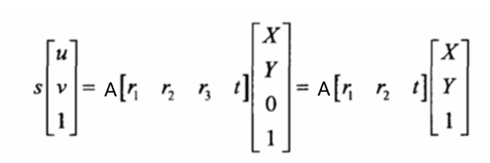
通过上面2.28与2.29得：

 ​​​

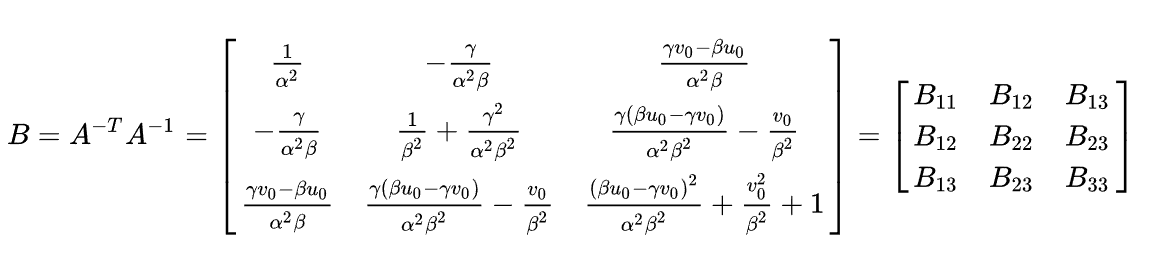
  可以自行计算B为对角矩阵，所以B只有6个未知数，所以向量b设置6个参数即可

 

第二部分 立体标定、立体校正与立体匹配

立体（双目）标定

        分别对双目的每个相机标定获得的外参通过代换推导得到双目相机中两个摄像头之间的相对位置关系。最终分别得到二者相对同一坐标系的旋转矩阵R和平移矩阵T能够使两个相机重合的过程。

立体校正（极线矫正）

        立体校正的目的就是，利用立体标定所获得的参数将实际非共面行对准的两幅图像，校正成共面行对准。当两个图像平面是完全共面行对准时，立体匹配的效率更高且计算立体视差是最简单的。因为当两个图像平面是完全共面行对准时，立体匹配从二维搜索降至一维搜索，并且可以过滤掉无匹配点。但是，在现实的双目立体视觉系统中，是不存在完全的共面行对准的两个摄像机图像平面的，所以我们要进行立体校正（共面行对准是指：两摄像机图像平面在同一平面上，且同一点投影到两个摄像机图像平面时，应该在两个像素坐标系的同一行）

校正：W是物点，M1,M2是投影点。最终实现R1,R2共平面且M1,M2两个像素坐标系在同一行立体

 

                                立体校正前

 

                                立体校正后

立体匹配（特征匹配、视差计算）

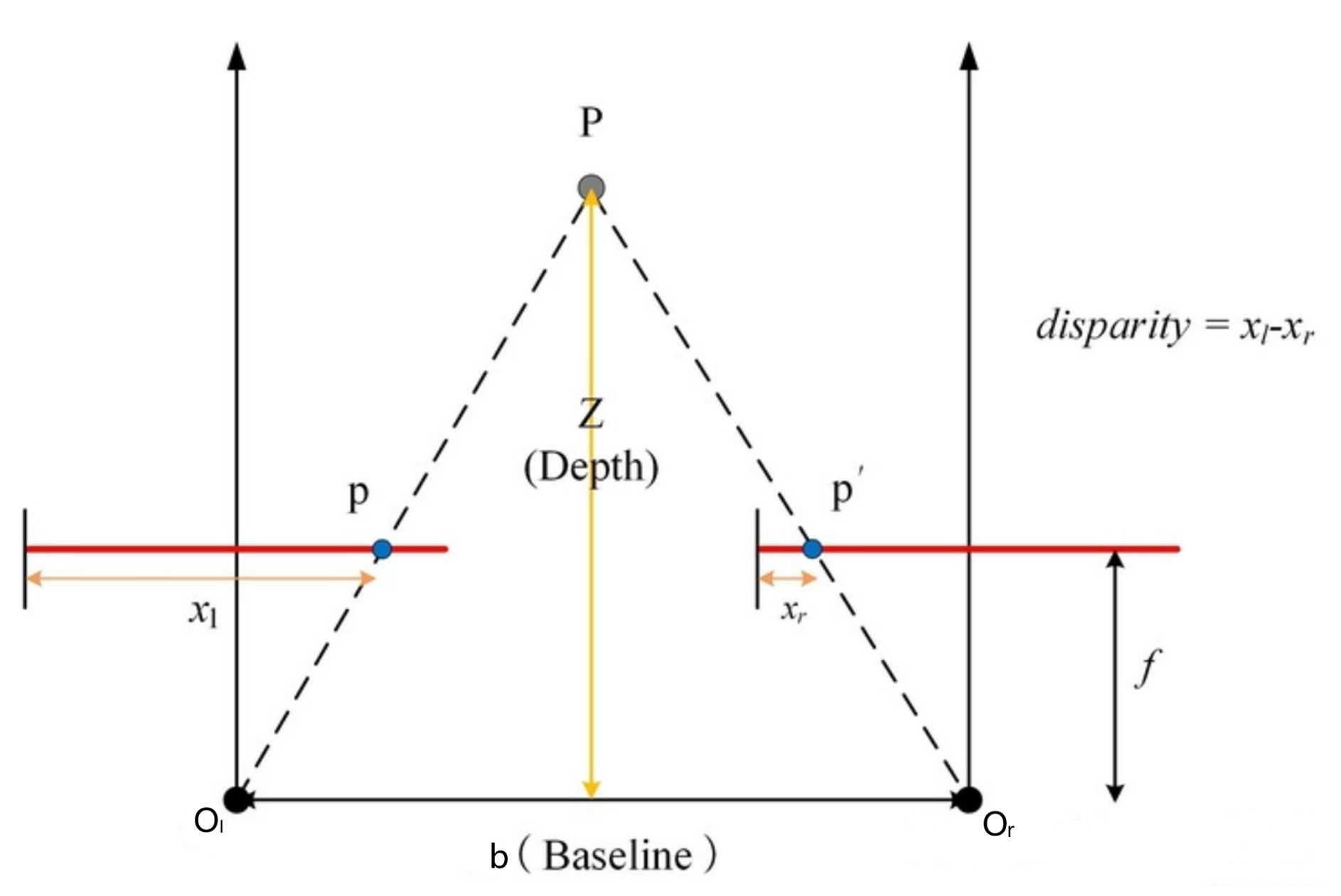
利用相似三角形原理

                  

化简后

                  

令视差d=xl-xr

                  

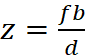
        保证左右相机进行深度感知的目标是同一个对象的像素点，例如的最优匹配点是。左右相机对同一个对象的像素点才能准确的利用视差计算出目标的深度信息。有诸多困难，如可能拍摄到的特征点模糊，可能有单个相机没拍摄到同一对象，所以匹配算法很重要。

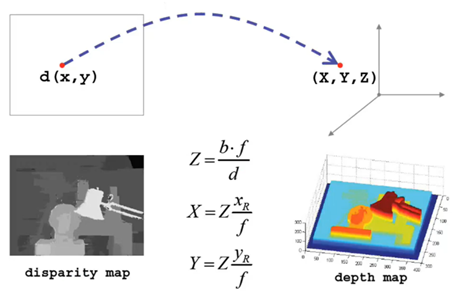
利用SGM做匹配的步骤，匹配方法如上所述，右视图中与左视图待测像素同一水平线上相关性最高的即为最优匹配。完成匹配后，我们需要记录其视差d,由深度计算公式已知，即可算出深度。

给定视差图、基线和焦距，三角测量计算3D空间中对应的位置

 

最后，三维重建效果展示：

（a）普通双目相机

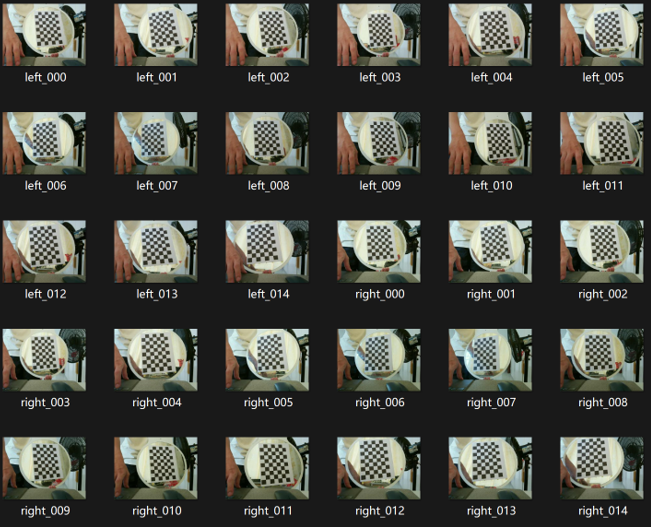
 （b）拍摄棋盘格

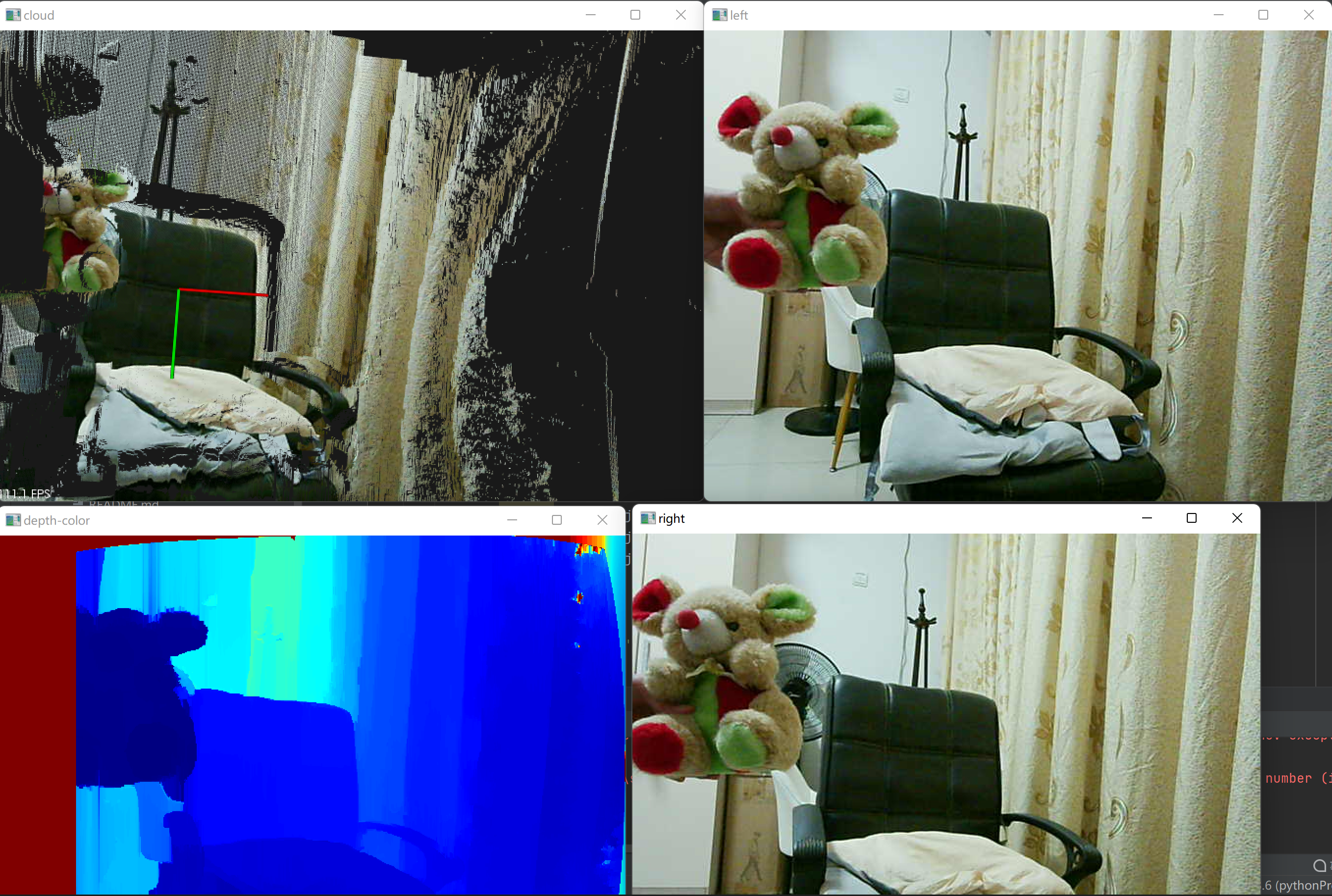
（c）三维重建效果

部分图片来自B站视频截图，欢迎交流学习。

本篇博客的完整内容可下载：单目、双目相机的标定原理以及图解_双目视觉标定原理-行业报告文档类资源-CSDN下载

强烈建议看这个文章：相机标定之张正友标定法数学原理详解（含python源码） - 知乎