强化学习——学习笔记_强化学习 csdn

一、什么是强化学习？

强化学习 (Reinforcement Learning, RL) 是一种通过与环境交互来学习决策策略的机器学习方法。它的核心思想是让智能体 (Agent) 在执行动作 (Action)、观察环境 (Environment) 反馈的状态 (State) 和奖励 (Reward) 的过程中，学习到一个最优策略 (Optimal Policy)，从而实现长期累积奖励最大化。

强化学习的核心框架包括以下几个部分：
智能体 (Agent)：在环境中执行动作，学习最优策略的实体；
环境 (Environment)：提供状态信息和奖励反馈，受到智能体动作影响的外部系统；
状态 (State)：描述环境当前状况的信息；
动作 (Action)：智能体可以在环境中执行的操作；
奖励 (Reward)：环境对智能体执行动作的评价，是一个标量值。
举一个小栗子，小明现在有一个问题，他要决定明天是学习还是去打球。现在就有两种可能性，打球和学习，如果现在的情况是，选择打球，那么小明将会受到批评，如果选择学习，他会受到奖励。显然，小明很大可能性会选择学习。这就是强化学习的内部机制。当对象在做一个决策的时候，算法会对每种可能性做一次函数计算，计算得到的结果叫做奖励值，奖励值会作为本次决策的重要参考标准。

具体的过程可以形象化为下图：

作为y一个高级的智能体，我们的大脑每时每刻都在进行决策，但是我们每个决策的过程就是这三个步骤：观察→行动→观测。我们通过观察周围的环境，然后做出相应的行动，然后在行动结束后，外界环境会给我们一个信号，这个信号是说我们的行动对外界造成了一定的影响，这些影响会得到一个结果（实际上就是上文说的奖励值），环境将影响通过这个信号让我们知道了。我们得到这个奖励值后，会根据新的环境和得到的奖励值，来进行下一个决策。

二、什么是马尔可夫过程？

强化学习问题通常可以建模为一个马尔可夫决策过程，包括以下几个要素：
1、状态集合 (State Set)：S；
2、动作集合 (Action Set)：A ；
3、状态转移函数 (State Transition Function)：$P(s^{\prime }\mid s,a)$，描述在状态s下执行动作a后转移到状态$s^{\prime }$的概率；
4、奖励函数 (Reward Function)：$R(s,a,s^{\prime })$，描述在状态s 下执行动作a并转移到状态s′后获得的奖励。
5、策略 (Policy)：$\pi (a\mid s)$，描述智能体在状态s下选择动作a 的概率。
q强化学习的目标是找到一个最优策略${\pi }^{\ast }$ ，使得长期累积奖励最大化。
说到这里还是没有说明什么是马尔可夫决策。我们可以看下图：

比如红绿灯系统，红灯之后一定是红黄、接着绿灯、黄灯，最后又红灯，每一个状态之间的变化是确定的。抑或是下图：
比如今天是晴天，谁也没法百分百确定明天一定是晴天还是雨天、阴天(即便有天气预报)。
对于以上的过程，我们假设有如下的状态转移矩阵(从一个状态到另外一个状态的概率)：
如果昨天是晴天，那么今天是晴天的概率为0.5，是多云的概率为0.375、是雨天的概率为0.125，且这三种天气状态的概率之和必为1。

以上就是马尔可夫决策过程的细节。
具体来说：
1、当且仅当某时刻的状态只取决于上一时刻的状态时，一个随机过程被称为具有马尔可夫性，比如我们在上面两幅图中的情况。
2、具有马尔可夫性质的随机过程便是马尔可夫过程。
在马尔可夫决策过程的基础上，再加上奖励机制，就可以得到马尔可夫奖励过程。

三、什么是马尔可夫奖励过程？

上面所提到的奖励机制包括奖励函数R和折扣因子γ两部分组成。
1、奖励函数：某个状态s的奖励R(s)，是指转移到该状态s时可以获得奖励的期望，有$R(s)=E[R_{t+1}|S_{t=s}]$。也就是在状态s下奖励的期望。
奖励函数又包括如下两类：
状态价值函数 (Value Function)：$V^{\pi }(s)$，描述在状态s下，依据策略$\pi$执行动作后能获得的未来累积奖励的期望。
动作价值函数 (Q-function)：$Q^{\pi }(s,a)$，描述在状态s下执行动作a 并依据策略$\pi$执行后续动作能获得的未来累积奖励的期望。
在目前多数的强化学习方法中，都是围绕动作价值函数展开研究的。

2、折扣因子 (Discount Factor)γ
γ取值范围为 [0, 1]，表示未来奖励的折扣程度。在这里有一种解释是当一个很久发生的动作所获得奖励会随着时间的推移而慢慢变小的，比如货币贬值的现象。在强化学习中这是一个超参数的存在。
如下式所示：

在上式中，G表示当下即时奖励和所有持久奖励等一切奖励的加权和(考虑到一般越往后某个状态给的回报率越低，也即奖励因子或折扣因子越小，用γ表示)。

四、什么是马尔可夫决策过程？

在上文中已经对马尔可夫奖励过程进行了基本的介绍，如果在马尔可夫奖励过程的基础上增加一个来自外界的刺激比如智能体的动作，就得到了马尔可夫决策过程通俗讲，马尔可夫奖励过程与马尔可夫决策过程的区别就类似随波逐流与水手划船的区别。具体来说，在马尔可夫决策过程中，$S_t$和$R_t$的每个可能的值出现的概率只取决于前一个状态$S_{t-1}$和前一个动作$A_{t-1}$，并且与更早之前的状态和动作完全无关。
当给定当前状态$S_t$(比如$S_t=s$)，以及当前采取的动作$A_t$(比如$A_t=a$)，那么下一个状态$S_{t+1}$出现的概率，可由状态转移概率矩阵表示。故有下式：

上式表达的意思为：在状态$s$下采取动作$a$后，转移到下一个状态$s^{\prime }$的概率。
假定在当前状态和当前动作确定后，其对应的奖励则设为$R_{t+1=r}$，状态转移概率矩阵类似为：

上式表达的意思为：在状态$s$下采取动作$a$后，转移到下一个状态$s^{\prime }$并获得奖励r的概率。
最终可以得到奖励函数即为：

上式表达的意思为：在状态s以及动作a的发生下，对所有接下来可能的奖励r求和，这里的r有不确定性，受环境所限制。
整个过程相当于将不同状态转移概率与对应的奖励r相乘并相加，以得到条件期望。
假设奖励是确定性的，则可以简化公式，去掉对r的求和，即：

因此上式就变为了只需要计算在状态s下采取动作a后，转移到下一个状态s′的概率乘确定的奖励r，然后对所有可能的下一个状态s′求和以得到条件期望。
这时我们还有一个疑问，如果环境反馈给我们一个现在智能体所处的状态，智能体要通过什么方式决定接下来的动作呢？这时就涉及到策略policy，策略函数可以表述为π
函数。
可得$a=\pi (s)$，意味着输入状态s，策略函数π输出动作a。
策略函数还有如下两种表达方式：
1、$a=\pi \theta (s)$
上式所要表达的意思为：当于在输入状态s确定的情况下，输出的动作a只和参数θ
有关，这个θ就是策略函数π的参数。举个例子就是y=wx+b中的w和b。
2、$\pi (a|s)=P(A_{t=a}|S_{t=s})$，
上式所要表达的意思为：相当于输入一个状态s下，智能体采取某个动作a的概率。

以上文中的天气状态为例：不同状态出现的概率不一样（比如今天是晴天，那明天是晴天，还是雨天、阴天不一定），同一状态下执行不同动作的概率也不一样（比如即便在天气预报预测明天大概率是天晴的情况下，你大概率不会带伞，但依然不排除你可能会防止突然下雨而带伞）。

经过上文的基本介绍之后让我们再重新定义一下最初提到的两个价值函数。
状态价值函数：

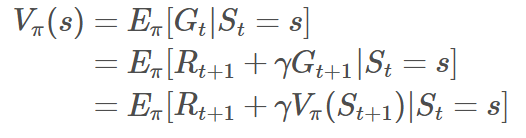
上式所要表达的意思就是从状态​s出发遵循策略π能获得的期望回报。
动作价值函数：

上式所要表达的意思就是当前状态s依据策略​执行动作​a得到的期望回报，记住这个函数，在接下来的算法中会常常涉及到，得到​Q函数后，进入某个状态要采取的最优动作便可以通过​Q函数得到​。
以上两个函数对应的流程如下图：

有了上述推导，我们可以知道Q函数怎么转换到状态价值函数的，如下式：

具体可以解释为下式，状态s的价值等于在该状态下基于策略π采取所有动作的概率与相应的价值相乘再求和的结果。

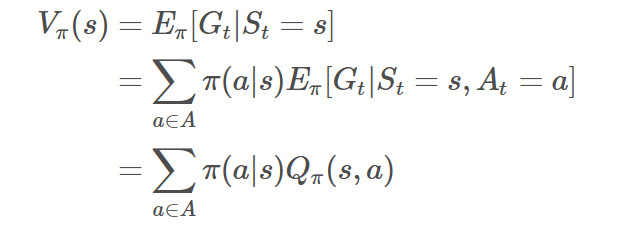
而从状态价值函数转换到Q函数如下式：

推导过程如下：

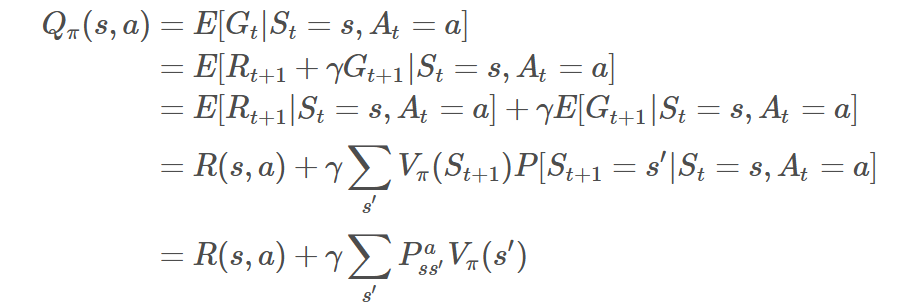
在状态s下采取动作a的价值等于当前奖励R(s,a)，加上经过衰减的所有可能的下一个状态的状态转移概率与相应的价值的乘积。
经过上式互相带入我们就可以得到马尔可夫决策的贝尔曼方程：

下图即为马尔可夫决策过程。

上图展示了在什么样的状态s下，有多少概率会做出动作a，这就是一个决策过程。如上图。当做出动作a，环境会给智能体反馈一个环境以及奖励。

整理自：https://blog.csdn.net/v_JULY_v/article/details/128965854