- 1Session,Application,cookie的区别_application对象、session对象和cookie对象都是保存数据,但三者有什么区别?
- 2百人畅玩,秒级开服:用华为云搭建《幻兽帕鲁》服务器就是不一样
- 3ESXI8.0下Ubuntu 20.04LTS安装VMTools_vmware tools 未由 vsphere 管理
- 4新手3分钟自动化搞定腾讯云《幻兽帕鲁》游戏服务器
- 5八大排序算法之快速排序(上篇)(未经优化的快排)_非优化排序
- 614 rtsp视频服务 基于 RTSPtoWeb 来转换为前端可用的服务
- 7C# Fleck实现websocket_c# fleck websocket 客户端
- 8python_scapy实现ARP扫描_scapy arp reply
- 9AttributeError: module ‘numpy‘ has no attribute ‘typeDict‘_attributeerror: module 'numpy' has no attribute 't
- 10CV 经典主干网络 (Backbone) 系列: CSPNet
特征值和特征向量及其在机器学习中的应用
赞
踩
特征值和特征向量是线性代数中的概念,用于分析和理解线性变换,特别是由方阵表示的线性变换。它们被用于许多不同的数学领域,包括机器学习和人工智能。
在机器学习中,特征值和特征向量用于表示数据、对数据执行操作以及训练机器学习模型。
在人工智能中,特征值和特征向量用于开发图像识别、自然语言处理和机器人等任务的算法。
1. 特征值 (λ):方阵 A 的特征值是一个标量(单个数字)λ,使得存在一个非零向量 v(特征向量),其中以下等式成立:
AV = λv
换句话说,当您将矩阵 A 乘以特征向量 v 时,您会得到一个新向量,它只是 v 的缩放版本(按特征值 λ 缩放)。
2.特征向量:上面提到的向量v称为特征值λ对应的特征向量。特征向量仅在乘以矩阵 A 时改变尺度(大小);他们的方向保持不变。
从数学上讲,要找到特征值和特征向量,您通常可以求解以下方程来得到 λ 和 v:
(A — λI)v = 0
在哪里:
- A 是您要查找特征值和特征向量的方阵。
- λ 是您要查找的特征值。
- I 是单位矩阵(对角线上有 1,其他地方有 0 的对角矩阵)。
- v 是您要查找的特征向量。
求解该方程涉及找到使矩阵 (A — λI) 奇异(即其行列式为零)的 λ 值,然后找到相应的 v 向量。
特征值和特征向量在机器学习和人工智能中的使用:
- 降维 (PCA):在主成分分析 (PCA) 中,您可以计算数据协方差矩阵的特征向量和特征值。具有最大特征值的特征向量(主成分)捕获数据中的最大方差,可用于降低数据集的维数,同时保留重要信息。
- 图像压缩:特征向量和特征值用于图像压缩的奇异值分解 (SVD) 等技术。通过用特征向量和特征值来表示图像,您可以减少存储需求,同时保留基本的图像特征。
- 支持向量机:支持向量机 (SVM) 是一种机器学习算法,可用于分类和回归任务。SVM 的工作原理是找到一个将数据分为两类的超平面。SVM的核矩阵的特征值和特征向量可以用来提高算法的性能。
- 图论:特征向量在分析网络和图方面发挥着作用。它们可用于查找社交网络或其他互连系统中的重要节点或社区。
- 自然语言处理 (NLP):在 NLP 中,特征向量可以帮助识别大型文档术语矩阵中最相关的术语,从而支持用于文档检索和文本摘要的潜在语义分析 (LSA) 等技术。
- 机器学习算法:特征值和特征向量可用于分析机器学习算法的稳定性和收敛性,特别是在深度学习中处理神经网络中的权重矩阵时。
特征值和特征向量的示例
示例 1:主成分分析 (PCA)
PCA是机器学习和数据分析中广泛使用的降维技术。它利用特征向量和特征值来减少特征数量,同时保留尽可能多的信息。
假设您有一个包含两个变量 X 和 Y 的数据集,并且您希望将其减少到一维。您计算数据的协方差矩阵并找到其特征向量和特征值。假设您获得以下内容:
- 特征值 1 (λ₁) = 5
- 特征值 2 (λ2) = 1
- 特征向量 1 (v₁) = [0.8, 0.6]
- 特征向量 2 (v2) = [-0.6, 0.8]
在 PCA 中,您将选择与最大特征值对应的特征向量作为主成分。在这种情况下,它是 v₁。您将数据投影到该特征向量上以将其减少到一维,从而有效地捕获数据中的大部分方差。
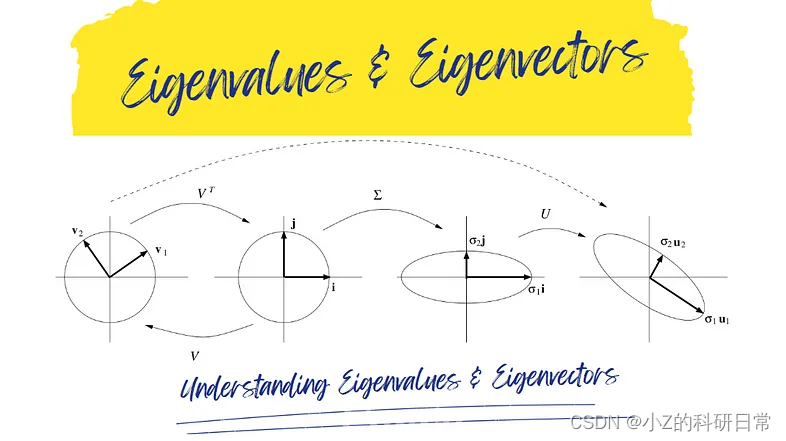
示例 2:使用奇异值分解 (SVD) 进行图像压缩
SVD 是一种矩阵分解技术,利用特征值和特征向量进行图像压缩。
考虑表示为矩阵 A 的灰度图像。对此矩阵执行 SVD 以获得三个矩阵:U(左奇异向量)、Σ(奇异值对角矩阵)和 V^T(右奇异向量)。
- Σ 中的奇异值代表每个分量在重建图像中的重要性。
- U 和 V^T 的列是 A 的协方差矩阵的特征向量。
通过仅保留奇异值的子集(及其相应的特征向量),您可以在压缩图像的同时保留其基本特征。这通常用于图像存储和传输等应用。
示例 3:Google PageRank 算法
特征向量在 Google 的 PageRank 算法中发挥着重要作用,该算法决定了网页在搜索结果中的重要性。在此算法中,网页表示为图中的节点,页面之间的超链接创建一个矩阵。
该矩阵的主特征向量表示网页的 PageRank 分数。相应的特征值有助于确定网页的整体重要性。这使得谷歌可以根据重要性对网页进行排名,帮助用户找到相关内容。


