A Distance Regularized Level-set Evolution Model Based MRI Dataset Segmentation of Brain‘s Caudate N_ddrtree 的 sigma 参数说明

A Distance Regularized Level-set Evolution Model Based MRI Dataset Segmentation of Brain’s Caudate Nucleus

基于距离正则化水平集演化模型的脑尾状核MRI数据集分割

大脑的尾状核与悲观情绪的情感决策高度相关，这是提高对抑郁症的理解和治疗的重要过程。尾状核的分割是该区域分析和研究过程中最基本的步骤。本文采用水平集法（LSM）进行尾状核分割。首先，提出了距离正则化水平集演化（DRLSE），区域可缩放拟合（RSF）和局部图像拟合（LIF）模型，用于脑磁共振成像（MRI）图像的尾状核的分割，以及分割结果通过使用选定的评估指标进行比较。所提出的三种方法的平均骰子相似性系数（DSC）值均超过85％，平均Jaccard相似性（JS）值分别超过77％。结果表明，这三种模型对强度不均匀的医学图像均具有良好的分割效果，满足一般分割要求，而所提出的DRLSE模型在分割方面表现较好。
关键词 距离正则化水平集演化，局部图像拟合，水平集方法，医学图像分割，区域可缩放拟合。

一，引言

随着科学技术的发展，先进的大脑成像技术和新型设备不断涌现。现有的大脑成像技术包括磁共振成像（MRI），正电子发射计算机断层扫描（PET），脑电图（EEG），磁脑成像（MEG），计算机断层扫描（CT），单光子发射计算机断层扫描（SPECT），扩散张量成像（DTI）等。这些脑成像技术已成为进行疾病诊断，手术计划和预后评估的必不可少的手段。并且，在通过这些成像技术获得的医学图像的分析过程中，医学图像处理是帮助研究人员提高医学图像的可读性和诊断效率的第一步。因此，医学图像处理已在全球范围内受到高度重视。图像分割不仅是图像处理的基础，而且是重点和难点，这是制约​​三维（3D）重建技术应用的瓶颈。医学图像分割的价值主要体现在以下两个方面：a）通过医学图像分割可以提取人体组织器官或病变组织，以协助诊断，治疗计划和临床研究。这样可以节省时间并有效减少诊断错误。 b）进行实时3D重建和可视化非常方便。 3D重建在计算上是昂贵且费时的，但是在临床医学中对实时3D重建的要求很高。对原始图像进行分割后进行压缩，降低了计算复杂度，使图像满足3D重建的实时性和精度。

传统医学图像分割是医护人员根据目标位置或实际解剖结构的实际情况通过手动分割完成识别工作的地方。尽管手动分割的结果最可靠，但是图像数据量如此之大，以至于图像分析和分割的工作量很大，并且这种工作量需要可靠的半自动或自动分割方案来完成以节省时间。随着计算机图像处理技术的发展，一些传统的图像处理方法已广泛用于医学图像分割中，并且新的分割方法不断涌现。其中，水平集方法可以自然有效地处理分裂和合并等拓扑变化，并且可以灵活地组合能量项，不仅可以分割普通图像，而且对复杂图像具有良好的分割效果。 因此，这一直是近年来研究的重点。区域可扩展拟合（RSF）模型是Li等人提出的基于区域的活动轮廓模型。 [1]，最初称为本地二进制拟合（LBF）模型[2]。通过调整水平设置函数和有符号距离函数之间的差异，此模型可确保计算准确，并避免重新初始化演化过程。局部图像拟合（LIF）模型[3]是从LBF模型发展而来的，它是一种由局部图像拟合能量驱动的新型主动轮廓模型。该模型使用高斯核代替传统的正则项来调节水平集函数，具有良好的分割效果和较高的计算效率。 Li等。文献[4]提出了距离正则化水平集演化模型（DRLSE），该模型消除了重新初始化的需要并保证了演化的稳定性。他们还将DRLSE应用于基于边缘的主动轮廓模型进行图像分割，并取得了良好的效果。后来，研究人员组合并改进了这些模型，并获得了许多新的实用医学图像分割方法。 Bhadauria和Dewal [5]提出了一种用于脑部CT图像出血检测的主动轮廓模型，该模型结合了空间模糊C均值（FCM）算法和RSF模型。这种组合的目的是将FCM聚类的结果应用于RSF模型的初始轮廓。丁等。 [6]通过另一个主动轮廓模型对强度不均匀的图像进行了分割，该模型将区域可缩放拟合能量与优化的拉普拉斯高斯（LoG）能量相集成。所提出的模型克服了对初始轮廓的敏感性问题，并且相对于其他基于区域的模型，实现了更高的分割精度和效率。 Wang等。 [7]基于LBF和LIF模型，构造了局部混合图像的拟合能量以获得新的主动轮廓模型，在准确性和有效性方面，其效果优于基于区域的模型。 Wang等。 [8]提出了一个新的基于区域的主动轮廓模型，具有混合区域图像拟合（HRIF）能量函数。使用两个不同的局部拟合图像定义了该能量函数。一种是扩展拟合图像（EFI），是局部拟合图像（LFI）[3]的扩展形式，另一种是方形拟合图像（SFI）。 Sethi等[9]定义了一种新的水平集方法，用于分割CT图像中的低对比度癌变区域，包括区域分离，区域增强和具有新的停止功能的DRLSE。结果显示了该方法在2D和3D CT图像上的优越性。 Liu等人[10]将基于边缘的DRLSE模型扩展到两级集合公式，并将其应用于从cine-MRI图像分割左心室和右心室，这有一定效果。 Zhang等[11]提出了一种基于DRLSE的前列腺癌MRI两步分割方法，实现了中央前列腺和前列腺周边的分割。他们使用多线段拟合方法来初始化水平集功能，这促使分割算法具有改进的边界收敛性。但是，它不能满足前列腺MRI不同扫描层中多区域条件的分割要求。 Gautam等[12]提出了一种混合方法，用于对出血性病变CT图像中的脑部病变区域进行分割，该方法结合了使用高切线函数和DRLSE函数的模糊聚类，从而以较高的分割精度获得了分割区域的平滑边界。 Wu等[13]提出了一种鲁棒且稳定的自动心脏运动跟踪方法。通过训练三层深玻尔兹曼机（DBM）建立心脏形状模型，然后将其作为形状先验项嵌入到DRLSE方法中，以约束演化形状以在电影MRI图像序列的每个帧上描绘心脏轮廓。这些出色的方法使更准确，更有效的医学图像分割成为可能，并为临床研究，疾病诊断和分类做出了重要贡献。

先前的研究表明，抑郁症，阿尔茨海默氏病（AD）和精神分裂症是最常见的疾病，同时对社会和经济发展也产生了巨大影响。然而，根据现有的医学图像分割研究，很少涉及尾状核分割。改进的水平集方法分割尾状核是有效的。它可以对原始MR图像执行降维，有助于提高医学图像的可读性，并提高分析效率。我们的研究将为AD和抑郁症等精神障碍的临床研究，疾病诊断和分类做出重要贡献。如何发现[14]，延迟，治疗和预测[15]脑功能障碍已成为医学研究人员的重点。 Al-shaikhli等人[16]提出了一种自动3D尾状核分割和基于结合字典学习和水平集公式的AD检测方法。分割率和分类准确率分别为91.5％和92.5％。此外，他们认为，尾状核萎缩的研究比全脑结构萎缩的研究对AD的检测有帮助。关于抑郁症，Ken-Ichi等人[17]的最新研究表明，刺激动物大脑的尾状核时会产生负面反应，从而证明了尾状核区域是造成悲观情绪决定的主要原因情绪。该研究有望帮助科学家更好地理解和治疗抑郁症。对于该领域的研究工作，最基本和必要的要求是尾状核的分割。通过分割尾状核，研究人员可以更直观，更清晰地观察该区域。对分割后的降维图像[18]的研究可以简化计算并提高分析效率。在本文中，使用半自动交互方法来形成初始轮廓框架。调整了根据现有MR图像数据集的参数设置，有效提高了尾状核的分割率。选择了RSF，LIF和DRLSE模型进行分割，结果表明，与地面真实图像数据集相比，该DRLSE模型具有最佳分割能力。本研究的参数设置和特征计算是新颖的，提出的尾状核MRI模型是可行和有效的。
本文的其余部分安排如下：在第2节中，介绍了水平集方法的原理和三个水平集模型。 然后，在第3节中，我们将对仿真实验设置进行详细说明。 结果和讨论在第4节中进行。最后，结语和将来的工作在第5节中进行讨论。

图1.医学图像分割方法。

二。 医学图像分割方法

A.医学图像分割方法

图像分割是医学图像处理中的一个基本但至关重要的步骤。 它是理解许多医学问题的重要基础和前提。 准确的医学图像分割结果可以为疾病的诊断和治疗以及制定临床治疗处方提供必要的基础数据。 一方面，医学图像具有特殊性，复杂性和部分体积效应的特征。 同时，它容易受到设备性能，对象移动，噪声和偏置场等各种外部因素的影响，这使得实际医学图像大多具有模糊和不均匀的特征。 另一方面，器官结构的复杂性和不规则性导致医学图像上的巨大差异。 由于上述原因，医学图像分割仍然是要解决的主要问题之一。
图像分割是将图像划分为感兴趣区域的过程，然后可以对其进行进一步分析和理解。根据图像的固有特征，例如灰度，颜色，纹理，对比度，局部统计特征和光谱特征，将图像分为具有各自特征的均匀区域。随着医疗保健的飞速发展，医学图像分割技术的研究与发展受到广泛关注，医学图像分割的新方法不断涌现。尽管有许多分割医学图像的方法，但是大多数方法基于不同的分割任务或不同的成像技术。这些方法通常具有很高的针对性，并且没有统一的标准来解决所有分割问题。医学领域中典型的医学图像分割方法可以归纳如下：基于区域的分割方法，基于边缘的分割方法以及基于特定理论的分割方法，其中一些最重要的方法如图1所示。（1 ）基于区域的分割方法根据不同区域中某些特征的相似性度量将图像划分为不同的子区域。它主要包括区域生长法，区域分割合并法和分水岭法。 （2）基于边缘的分割方法通常通过利用不同区域之间的像素度的不连续性来检测区域之间的边缘以实现分割。它包括微分算子和活动轮廓模型。 （3）分割方法基于特定的理论-随着计算机视觉和人工智能的迅速发展，新的研究成果被引入医学图像分割中。常见的方法包括：基于小波分析和变换的多尺度分割技术，基于随机场理论的分割技术[19]，基于模糊理论的分割技术[20]，基于遗传算法的分割技术[21]，[22] ]，基于水平集理论的分割技术，基于人工神经网络的分割技术[23]，[24]。

B.水平集方法

水平集方法主要是从界面传播领域发展而来，是一种用于界面跟踪和形状建模的数值技术。 1988年，Osher和Sethian [25]首次提出了水平集的概念，该概念主要用于根据热力学方程式求解火焰的形状变化过程。 由于火焰形状的高动态性和拓扑结构的不确定性，很难用传统的参数形式描述火焰形状的变化。 因此，他们提出了一种水平集的概念来描述与时间有关的运动界面。

水平集方法的核心操作是隐式将二维曲线表示为三维连续函数曲面的零水平集。通过不断更新水平集函数，更改零水平集以实现曲线的连续演变。可以说，其本质是求解偏微分方程。该方法的重要理论前提是隐函数的概念。将水平集概念引入曲线演化理论的目的是为曲线提供隐式表达式，从而避免了由参数化的显式表达式引起的一系列问题。隐式表达式在描述曲线运动时具有明显的优势。例如，当多条曲线在运动中合并为一条曲线，或一条曲线分裂为多条曲线时，这种拓扑变化无法通过连续参数曲线的运动来表示。但是，上述曲线的拓扑变化可以表示为连续变化的曲面与固定平面（例如z轴为零的平面）的相交线的变化，这使得复杂的曲线运动过程转变为高维函数的演化。如果水平设置功能仍然是有效功能，则该功能中隐含的曲线可以在任何拓扑中进行更改。这是解决参数化方法不能满足拓扑变化问题的很好的解决方案。因此，与传统的图像分割方法相比，水平集方法具有明显的优势：隐式表示的演化曲线（或曲面）可以自然地改变其拓扑结构，从而可以在图像中分割具有复杂形状的对象。它可以避免跟踪闭合曲线（或曲面）的演化过程，并将曲线（或曲面）的演化转化为偏微分方程的数值解。由于其强大的理论背景，它还可以轻松扩展到高维案例。由于这些优点，水平集方法在医学，材料力学，流体力学，计算机视觉等方面具有广泛的用途。
二维平面上的闭合曲线定义为y = f(x)，或写为y − f(x)=0。如果我们假设φ(x,y)= y − f(x)， 则φ（x，y）= 0是曲线y = f（x）的隐式表达式。 水平集的演变规律可以进一步分析。 如果函数φ（C，t）是一个集合，则与时间t处的曲线C（t）对应的零水平集为：

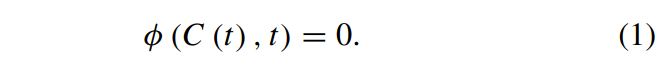
上式的偏导数为：

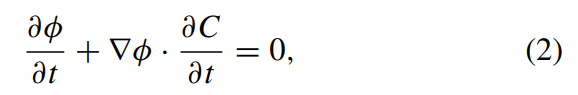
其中，∇φ是φ的梯度。 令C的弧长参数为s。 根据曲线演化理论和水平集的概念，φ沿C切线的变化为∂φ/∂s= 0，即：

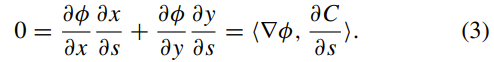
∇φ垂直于切线∂C/∂s，该切线与法线方向一致。 如果将φ指定为零水平集内的负值，并指定零水平集外的正值，则水平集曲线的单位法向矢量为：

其中，F是曲线的速度函数。 最后，通过组合方程（2），（4）和（5），可以得到由水平集函数表示的曲线演化方程，如下所示：

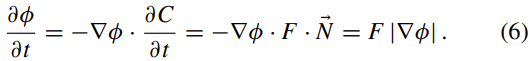
总之，水平集方法是将闭合曲线的演化转换为水平集函数的演化，然后求解相应的偏微分方程的过程。

C.水平集模型的分类

水平集模型主要分为两类：基于边缘的水平集模型和基于区域的水平集模型。
1）基于边缘的水平集模型
这样的模型使用局部边缘信息来使演化曲线近似于目标轮廓。因此，它们更适合于分割具有强边缘的图像。但是，由于这种模型过于依赖目标边缘的梯度信息，因此其逼近效果对于边缘没有明显梯度变化的图像而言并不理想。演化曲线通常会越过边缘，导致分割效果不佳。最著名的基于边缘的水平集模型是Kass等人提出的Snake模型[26]。其主要原理是为目标的初始轮廓设置边缘功能，然后驱动力驱动初始轮廓曲线向最大梯度收缩。当函数获得最小值时，将获得最终的分割结果。该模型的缺点是它对初始轮廓位置敏感，并且可能会陷入局部最优状态。在凹面区域几乎没有收敛。针对不容易发现凹陷区域边缘的问题，提出了梯度矢量流（GVF）模型[27]，该模型可以通过梯度矢量流代替梯度矢量流来检测目标井的凹面边界。传统的外力场。 Li等人[4]提出的DRLSE模型是一种非常实用的基于边缘的水平集模型。
2）基于区域的水平集模型
基于区域的水平集模型通常是通过约束（例如轮廓曲率和目标区域的面积）分割的图像。 最典型的是C-V模型[28]。 但是，假定图像灰度在每个区域中均一分布。 因此，难以分割对比度弱且亮度不均匀的医学图像。 而且，由于不断地初始化函数，该模型很耗时。 Li等人[1]提出的RSF模型和Zhang等人[3]提出的LIF模型都属于基于区域的水平集模型。
D.水平集模型算法
下面简要介绍三种级别集模型，即RSF模型，LIF模型和DRLSE模型。 然后将在此基础上进行仿真实验。
1）区域可调整拟合（RSF）模型
本节介绍RSF）模型[1]。首先，定义了由轮廓和两个拟合函数组成的可区域缩放的拟合能量函数。最佳拟合函数用于提取轮廓两侧的局部灰度平均值作为局部区域信息，以构造能量函数。由于核函数具有比例参数，因此区域可缩放的拟合能量可以使用可控制范围内从小区域到整个区域的区域灰度信息，从而将轮廓驱动到目标边界。因此，该模型可用于分割灰度不均匀的图像。可将区域可缩放拟合能量合并到带有正则化项的变化水平集公式中，从中导出用于能量最小化的曲线演化方程。该模型可以避免重新设置电平设置功能，提高运算速度。该模型定义为：

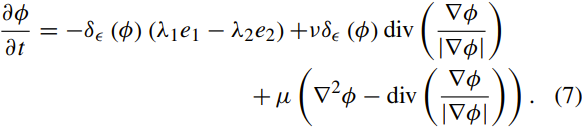
右侧的第一项称为区域可缩放拟合能量项，负责将活动轮廓朝对象边界驱动。 拟合能量的区域可缩放性质可以通过更改参数σ的大小来表示。 第二项对零级轮廓具有缩短或平滑作用，因此它被称为弧长项。 最后一项是正则化项，因为它用于维护级别设置功能的正则性。 ∇是Laplacian运算符，而div（）是散度运算符。 λ1，λ2，ν和μ是可以根据实际图像进行修改的常数。 函数H在此模型中是平滑函数，通常用于近似Heaviside函数：

H的导数为

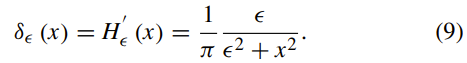
e1和e2定义如下：

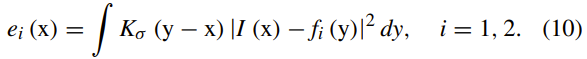
选择核函数K作为高斯内核：

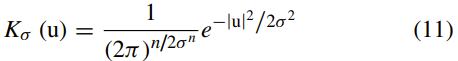
比例参数σ>0。并且：

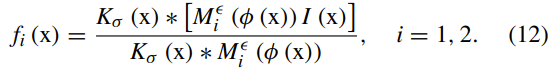
其中M1（φ）= H（φ）> 0且M2（φ）= 1 − H（φ）>0。因此，（12）中的f2也可以写成：

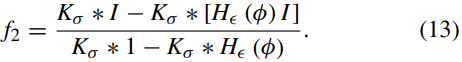
算法1是RSF算法的伪代码。

2）本地图像拟合（LIF）模型
通过考虑RSF模型，Zhang等[3]提出了一种由局部图像拟合能量驱动的新型主动轮廓模型。 他们用局部图像拟合能量替换了RSF算法中的局部强度拟合能量，然后通过最小化拟合图像和原始图像之间的差异来获得局部图像拟合能量函数。 他们使用高斯核而不是传统的正则化项对水平集函数进行正则化，因此该模型也可以命名为高斯正则化水平集模型。 该模型不仅可以获得与LBF能量模型相似的分割结果，而且还可以保持子像素精度和边界正则化属性。 最重要的一点是它的计算效率更高。
张将本地拟合图像（LFI）定义为：

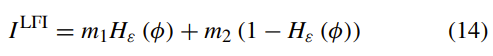
其中m1和m2定义如下：

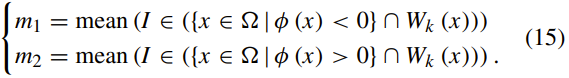
其中，Wk（x）是一个矩形窗口函数，例如截断的高斯窗口函数或常数窗口函数。 则局部图像拟合能量函数为：

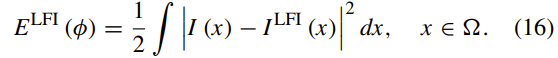
最后，Zhang将φ的ELFI（φ）最小化，以获得相应的梯度下降流：

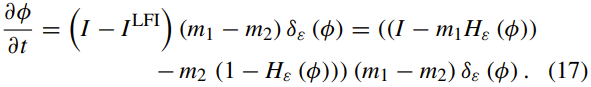
上式中的Hε（x）和δε（x）项可以从（8）和（9）中找到。 m1和m2的计算与（12）相同。
算法2是LIF算法的伪代码。

3）距离调整水平集演变（DRLSE）模型
Li等人[4]基于传统的基于边缘的水平集分割算法提出了一种改进的变分水平集公式。 他们提出了一个新的能量项，称为距离正则项，以限制水平集函数在整个迭代过程中保持稳定。 它有效地克服了传统的水平集算法在迭代过程中需要重新初始化水平集函数的问题，提高了分割速度。 同时，该算法提出的距离正则项可以移植到另一个水平集算法模型中，取得良好的效果。

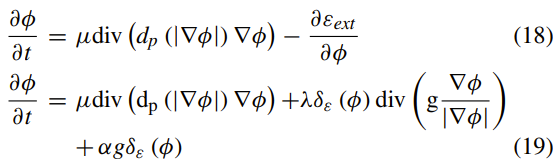
等式（18）是DRLSE的一般形式。 等式（19）是将DRLSE应用于基于边缘的活动轮廓模型时的形式。 第一项在eqn中位于右侧。 （19）被称为距离正则项，它与势函数相关联，而第二和第三项与加权长度项和加权面积项相关联.μ是常数，div（）是发散算子和dp 由以下方式定义：

其中，p是距离正则化的潜在函数。 单阱势p1的简单定义是：

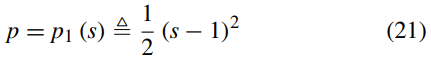
应该注意的是，对于距离正则化，双阱势p2是更好的势函数：

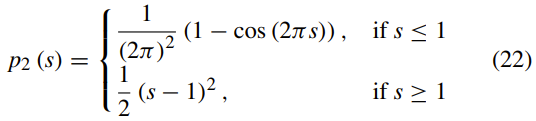
p2的一阶和二阶导数由下式给出：


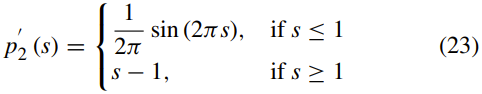
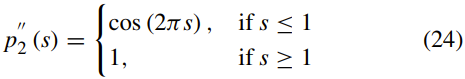
函数dp（s）= p02（s）/ s满足：

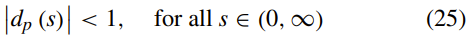
并且：

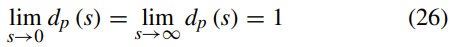
另外，λ＞ 0和α∈R是边缘项和面积项的系数。 g是边缘指示函数为：

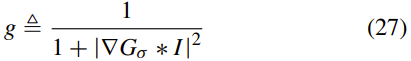
其中Gσ是具有标准偏差σ的高斯核，I是域上的图像。 根据Li et al [4]，δε定义为：

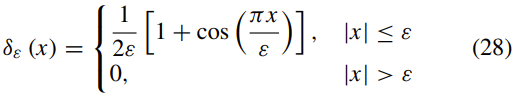
三， 实验设计

A.数据准备
实验中使用的数据集来自Openneuro。1从公共MRI数据集下载的文件格式为“ .nii”，其中包含图像和图像信息。 从数据集中获得的扫描结构图像（T1加权FLASH（快速低角度拍摄），TR（重复时间）= 12毫秒； TE（回波时间）= 5.6毫秒； 1 mm3分辨率）[29]已进行了预处理。 与头骨剥离。 然后，通过MATLAB中的NIFTI工具包读取这些文件，并挑选出18个轴向切片并将其另存为JPG图像，以进行尾状核分割实验。 图2显示了所有原始图像。
B.实验流程图
三种模型的实验步骤基本相同，分为五个步骤。 图3给出了实验流程图。

C.每个模型的参数设置
1）比较实验中RSF和LIF的参数设置
这三个模型的初始轮廓是通过[x，y] = ginput（n）函数生成的，该函数可以从当前图形中选择n个点，并返回这些点的相应坐标矢量x，y。 鼠标可以定位N个点。 我们使用鼠标在目标区域上定位了四个点，以将初始轮廓生成为两个矩形。 在第一个实验中，为两个模型构建了相同的初始水平集轮廓。 比较了两种方法的分割效果和效率。 这两个模型采用的参数是：在RSF模型中，timestep= 0.125，mu = 1，iterNum = 150，lambda1 = 1.0，lambda2 = 1.3，nu = 0.001×255×255，ε= 0.1，sigma = 0.8。 在LIF模型中，timestep= 0.1，epsilon = 0.2，sigma = 0.6，sigma_phi = 1，iterations= 200。
由于MRI图像具有强度不均匀性，因此难以将尾状核与灰质分离。 面对这个问题，选择了一个小的sigma以使分割结果在RSF模型中更加准确。 另外，λ2的值大于λ1。 这是为了避免远离初始轮廓的新轮廓，并确保最终轮廓更接近目标边界。 δε（φ）的轮廓受参数ε的影响。 较大的ε引起较宽的轮廓，从而扩大了捕获范围，但降低了最终轮廓的精度。 我们想要分裂的尾状核相对较小，因此选择了较小的ε。 ν的值设置为0.001×255×255。较大的ν会进一步影响轮廓的长度，但在某种程度上也不利于轮廓的扩展。 因此，可以在需要时稍微调整此参数值。
在LIF模型中，仍然选择了一个小的sigma以使分割结果准确。 根据图像和经验，将sigma的值选择为0.6。 此外，根据实验，正则化高斯核的标准偏差sigma_phi应在0.45和1之间选择。 图像的噪点越高，应将sigma_phi设置得越大。 在这里，sigma_phi =1。为了提高效率，可以将高斯核的大小截断为5×5的掩模。
2）三种模型的参数设置
在这一部分中，使用RSF，LIF和DRLSE模型对尾状核进行分割，然后对分割结果进行比较和评估。 尽可能为每个模型选择最佳实验参数，以获得最佳分割效果。 DRLSE模型的参数设置为：timestep = 5，mu = 0.2/timestep，iter_inner = 5，iter_outer = 40，lambda = 5，alpha = -1.5，ε= 1.5，sigma = 0.8。
在DRLSE模型中，由于算法的改进，可以使用相对较大的时间步长来显着减少迭代次数并提高效率。 在此，时间步长被设定为5。加权长度项λ的系数被设定为5。加权面积项α的系数被设定为-1.5。 应该注意的是，当初始轮廓在目标对象内部并且轮廓需要向外扩展时，alpha应该取负值。 相反，如果初始轮廓在目标对象之外，则alpha取正值，轮廓向内收缩。 对于边界较弱的图像，alpha值应相对较小以避免边界溢出。 Epsilon通常设置为1.5。 对于sigma，如果从内到外执行演化轮廓，则sigma取较小的值。 相反，sigma值较大。

对RSF模型中的参数设置进行了细微调整。 时间步长调整为0.1。 在LIF模型中，参数不会更改。
D. EXPERIMENTAL PLATFORM
All experiments were conducted on a standard PC (Intel Core ™ i7-8750H, 2.20 GHz processor with 8 GB of RAM). The algorithm was implemented in Matlab r2016a.

IV。结果与讨论

A.RSF和LIF模型的分离结果
在这组实验中，我们手动选择了相同的初始水平集函数（矩形初始轮廓）。通过水平集迭代，获得了两个模型的分割结果和迭代时间。在图4中，（a）是原始图像，（b）至（f）是感兴趣区域（ROI）的缩放图像。 （b）是相同的矩形初始轮廓图像，（c）是RSF模型的分割结果，（d）是LIF模型的分割结果，（e）是RSF模型的分割结果的二值图像。 （f）是LIF模型分割结果的二值图像。从图4可以很容易地看出，对于相同的分割区域（尾状核），通过设置相同的初始水平设置函数（矩形轮廓）获得的两个模型的分割结果基本相似。但是，经过仔细观察，发现存在细微差异。 RSF模型的分割轮廓比LIF模型更平滑。 RSF模型通过轮廓两侧局部区域的强度信息引导轮廓运动，并且演化方程中的弧长项对轮廓具有一定的平滑效果。 LIF模型限制了轮廓的运动，该轮廓限制了根据本地图像信息构造的拟合图像和原始图像之间的差异。该模型删除了传统的正则化项，并采用了高斯核对水平集函数进行正则化，并在每次迭代后平滑轮廓。 LIF模型可以实现亚像素分割精度。 LIF模型的分割轮廓比RSF模型更粗糙。

图5展示了两个模型下所有实验图像的水平集迭代的运行时间。 横轴是图像编号，纵轴是运行时间。 根据对分割结果的影响，LIF模型中的迭代次数为200，而RSF模型中的迭代次数为150。 可以看出，尽管LIF模型比RSF模型有更多的迭代，但是它的运行时间仍然比RSF模型短，这证明了Zhang等人在文献中提到的LIF模型比RSF模型更有效[3]。
B.与RSF，LIF和DRLSE模型的比较
在本节中，这三个水平集模型用于分割尾状核。 参考图像用作地面真相（GT）来比较模型的分割结果。 已获得经验丰富的医生的手动注释以供参考。

1）主观评价结果
图6依次显示了地面真实情况，RSF模型，LIF模型，DRLSE模型及其二进制图像的分割结果。 （a）至（h）是感兴趣区域（ROI）的缩放图像。直观地讲，这三种方法可以很好地分割尾状核。从图6可以很容易地看出DRLSE模型的分割结果最接近地面真实情况，其轮廓最平滑。 DRLSE模型使用具有双阱势能p2的能量项（称为距离正则项）来约束水平集函数，使其在整个迭代过程中保持稳定和平滑。水平集演化过程结束后，模型通过进一步的Alfa = 0的水平集演化重新建立零水平轮廓，从而得到更平滑的分割轮廓。由于LIF模型可以实现亚像素级的精确分割，因此与其他两个模型相比，它可以获得略微粗糙的分割轮廓。然而，当将结果与地面真实图像进行详细比较时，仍然观察到分割不足或分割过度的现象。从（f）中可以看出，尾状核的上半部分被过度分割。与地面真像相比，（d）和（f）中的尾状核的下半部分显示了分割不足的问题。原因之一可能是算法对初始轮廓的敏感度使最终轮廓不太接近目标轮廓。这些模型的分割精度在很大程度上取决于初始轮廓的选择。另外，模型的参数可能不够鲁棒。图像之间的差异导致模型参数自适应的差异。需要一套适用于所有实验图像并获得良好分割精度的合适参数。第三个原因可能是图像质量不够高。尾状核小，边界模糊，因此难以准确分割。即使有经验的医生手动分割尾状核，边缘也会有一些小错误。
2）定量评估
使用以下指标[30]，对真实情况和细分结果进行了定量比较：对于每个细分结果，真正（TP），真负（TN），假正（FP）和假负（ FN）计数被计算。 这些指标定义为：

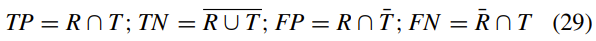
其中T是代表基本事实的真实集，R是代表分割结果的结果集。 三种测试模型之间的比较是根据以下性能指标进行的，包括Dice相似性系数（DSC），雅卡德相似性（JS），灵敏度（正确检测出的阳性分数），和特异性（正确检测出的阴性部分）。
Dice系数：

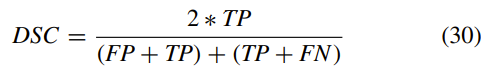
Jaccard similarity:

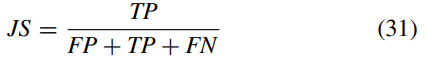
Sensitivity:

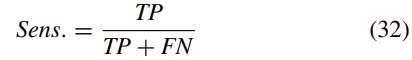
Specificity:

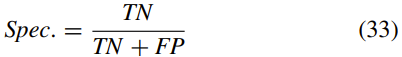
DSC和JS都用来表示分割结果和地面真实值之间的相似性。 在两个细分之间完全匹配的情况下，该度量取值为1，即，值越接近1，则细分结果的相似性就越高。 当分割结果相似时，JS比率比DSC敏感。 此外，当灵敏度高时，丢失的分割率低，而当特异性高时，错误的分割率低。
实验结果的相应指标值列于表1-4。从表1中可以看出，三个模型的DSC值主要在80％以上，表明这些模型都可以获得良好的分割结果。 由于JS对于类似的细分结果比DSC更为敏感，因此其值通常低于DSC值。
最后，我们使用JS作为标准来排除分割效果较差的两个组。 然后，我们将剩下的数据取平均值，以创建表5所示的结果。表5显示了这三个模型之间的性能比较。 结果表明，这三种算法的分割性能都很好，其中DRLSE模型优于其他两种模型。

五，结论

本文的目的是通过考虑与劳动密集型手动分割相比尾状核的半自动分割来帮助精神疾病（例如抑郁症）的诊断和治疗。鉴于水平集方法在分割强度不均匀的医学图像方面的优势，我们将这种方法应用于大脑的MRI图像以分割尾状核。选择了RSF，LIF和DRLSE模型进行细分。将所有分割结果与地面真实图像进行比较，地面真实图像是由经验丰富的医疗从业人员进行的手动分割图像。提出的三种方法分别实现了平均骰子相似性系数（DSC）值为0.8691、0.8722和0.9017，平均Jaccard相似性（JS）值分别为0.7704、0.7747和0.8223。结果表明，在这三个模型中，DRLSE模型具有最好的分割能力，并且每个指标的平均值最高。尽管其他两种方法稍差一些，但它们仍可以可靠地从图像中分割尾状核并满足常规分割要求。当传统的分割算法无法获得令人满意的结果时，就需要探索混合分割技术。另外，需要实施其他不同的指标来进一步评估细分结果。
在当前的研究中，主要重点是算法开发，并将其部署在开放访问数据集上。 所提出的技术已部署在有限大小的公共数据库中，并且正在收集更多相关数据。 作为将来的工作范围，将使用更大的数据池。 除了这种自动初始化，还将考虑证明所提出技术的鲁棒性和有效性，然后进行调查以寻找从所得结果中得出的任何结论或统计分析的可能性。