- 1微信小程序原生开发功能合集十五:个人主页功能实现_小程序个人主页
- 2Kotlin初级【基本语法、数据类型、循环】
- 3Android Log 打印日志工具Logcat_androidstudio 打印日志插件
- 4安卓命名规范_android 包名规范
- 5Android学习札记8:对TextView中的文字中间加上横线_安卓textview 一个数字加一条横线怎么弄
- 6Dbeaver,Hudi,Hive,Spark,Presto应用问题及解决措施梳理
- 7PS工具的概述_ps中的矩形工具英文字母的来源
- 8【网站项目】房屋租赁系统
- 9Vue利用递归实现简单的目录树结构
- 10【Web实战】零基础微信小程序逆向(非常详细)从零基础入门到精通,看完这一篇就够了
割平面法(Cutting Planes )
赞
踩
有效不等式 (Valid Inequalities)、 割平面(Cutting Plane)算法
(1)最可能的结果和理想约束都是由![]() 提供
提供
(2)目标:通过给定的已知条件,找到有效方法来近似获得![]()
(3)通过生成线性不等式(所有整数解均满足)来加强约束,这种不等式称为有效不等式
定义6:对于所有 均满足
均满足 。那么对于
。那么对于 ,不等式
,不等式 是一个有效不等式
是一个有效不等式
其中,![]() 有效,当且仅当X落在半平面
有效,当且仅当X落在半平面![]() 中
中

(1)0-1背包问题
![]()
(a) 如果![]() ,那么
,那么![]() (不成立),因此
(不成立),因此![]()
(b) 如果![]() ,那么
,那么![]() (x3,x5取0,x4取1),因此
(x3,x5取0,x4取1),因此![]() (x1不大于x2,)(1,1;0,1;0,0)
(x1不大于x2,)(1,1;0,1;0,0)
(2)混合整数集
![]() (x 为 连续值, y 为整数)
(x 为 连续值, y 为整数)

其中不等式![]() 是有效的,并提供了X的凸包
是有效的,并提供了X的凸包
(3)近似(Rounding )
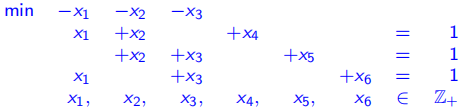
(a) 对三个约束 使用![]() 进行线性组合
进行线性组合
![]()
(b) 对一些系数进行降低(reducing),或者使用![]() 替代(substituting)
替代(substituting)![]()
![]() (将1/2 用“0” 代替,因为都为正整数,所以变为小于号)
(将1/2 用“0” 代替,因为都为正整数,所以变为小于号)
(c) 左端项为整数,因此右端项必然![]()
每个变量均为正整数,可以将3/2 改为“1”
(d) 最终的不等式变为:![]() , 切掉了LP问题的最优解
, 切掉了LP问题的最优解![]()
![]()
生成有效不等式的方法
(1)如果![]() 是可行整数解集,并且
是可行整数解集,并且![]() 是问题约束的线性松弛的可行域,那么除非
是问题约束的线性松弛的可行域,那么除非![]() (P为所有整数解X的凸包),那么存在有效不等式对于
(P为所有整数解X的凸包),那么存在有效不等式对于![]() 有效,但不满足P。(包含凸包的更小可行域)
有效,但不满足P。(包含凸包的更小可行域)
(2)生成有效不等式的方法:
(a)近似(rounding)
(b)模运算(Modular arithmetic )
(c)混合整数近似(Mixed integer rounding)
(d)吸取(Disjunctions)
(e)添加(Superadditivity)
Rounding:
(1)此方法基于下面两个现象:
(a) 如果,![]() ,那么
,那么![]() (x取不大于a的最大整数,向下取整)
(x取不大于a的最大整数,向下取整)
(b) 如果 ![]() 包含X的有效不等式,且
包含X的有效不等式,且![]() ,那么
,那么![]() 对于
对于![]() 依然有效 (等式两边同时乘以一个大于“0”的数,不等式不变号)
依然有效 (等式两边同时乘以一个大于“0”的数,不等式不变号)
(2)令 ![]() 为矩阵
为矩阵![]() 的列,且
的列,且
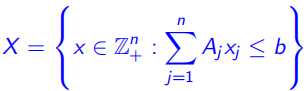
定义7(有理多面体,Rational Polyhedron):如果存在一个带有合理系数的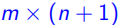 大小的矩阵
大小的矩阵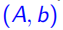 使得
使得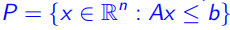 ,那么这个多面体是有理的(rational )
,那么这个多面体是有理的(rational )
Chv´atal-Gomory Procedure
(1)选择![]() ,并计算矩阵
,并计算矩阵![]() 行的一个线性组合:
行的一个线性组合:
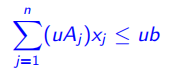
(2) 将系数![]() 向下取整(Round down):
向下取整(Round down):
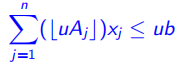
(3) 将右端项![]() 向下取整(Round down):
向下取整(Round down):
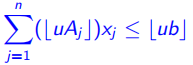
通过改变![]() ,我们得到第一个Chv´atal 封闭多面体
,我们得到第一个Chv´atal 封闭多面体 ![]()
![]() :
:
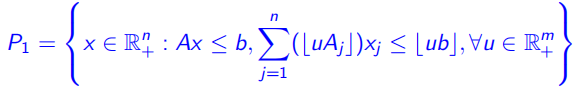
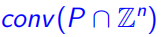 的线性描述
的线性描述
定理1: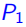 是一个多面体
是一个多面体
给定![]() 是一个有理多面体,可以再次对
是一个有理多面体,可以再次对![]() 使用近似(rounding)操作,从而得到
使用近似(rounding)操作,从而得到![]()
从而可以得到一系列的多面体:
![]()
定理2:对于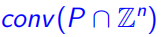 每个有效不等式可以使用Chv´atal-Gomory操作在有限次后得到
每个有效不等式可以使用Chv´atal-Gomory操作在有限次后得到
定理3:令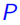 为一个有理多面体,那么我们可以得到
为一个有理多面体,那么我们可以得到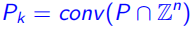 ,对于
,对于
定义8(Chv´atal 的秩):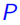 为一个有理多面体,Chv´atal 的秩为最小整数k,使得在第k次得到凸包
为一个有理多面体,Chv´atal 的秩为最小整数k,使得在第k次得到凸包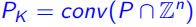
图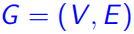 的匹配问题
的匹配问题
(1)对于图![]() ,匹配(matching)
,匹配(matching)![]() 是不相连的边(disjoint edges)的集合,
是不相连的边(disjoint edges)的集合,
比如,每个子图![]() 中的节点,不出现在第二条边上
中的节点,不出现在第二条边上


