图的最小生成树（Prim算法）_用prim算法生成下图的最小生成树

最小生成树

定义：生成树中边的权值（代价）之和最小的树

Prim

Prim算法：普里姆算法，图论中的一种算法，可在加权连通图里搜索最小生成树。

Ps：该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克（Vojtěch Jarník）发现；并在1957年由美国计算机科学家罗伯特·普里姆（Robert C. Prim）独立发现；1959年，艾兹格·迪科斯彻再次发现了该算法。因此，在某些场合，普里姆算法又被称为DJP算法、亚尔尼克算法或普里姆－亚尔尼克算法。

算法的具体思路

①建立一个数组Info[ ]，用以存储图中所有点到最小生成树的距离
②取出一个顶点加入最小生成树，根据二维数组来获取图中所有顶点到该点的距离，并更新数组Info[ ]
③根据所更新的数组Info[ ]，定位到最小生成树最短距离的顶点
④将该顶点加入到最小生成树中，并更新数组Info[ ]：
若未加入顶点到新加入的顶点的距离小于原先顶点到最小生成树的距离，则对Info数组进行更新
⑤重复③④操作，直至数组Info[ ]的所有数值为0，即所有顶点都存在于最小生成树中

图解

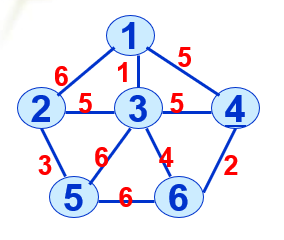
①新建数组为Info[6]：info[a-1]（数组从零开始），表示顶点a到最小生成树的距离

②加入第一个顶点为1，更新数组为{0,6,1,5,max,max}（max表示最大值）

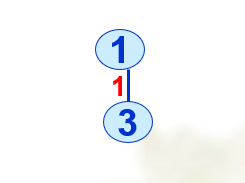
③从中找出最小值为1，对应的顶点为3，加入最小生成树
找出3到其他最顶点的距离{1,5,0,5,6,4}与之前得出的{0,6,1,5,max,max}比较，将小值进行替换，即更短的路径，得到更新数组为{0,5,0,5,6,4}

④从中找出最小值为4，对应的顶点为6，加入最小生成树
重复之前的操作，得到相应

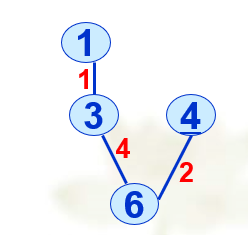
⑤

⑥

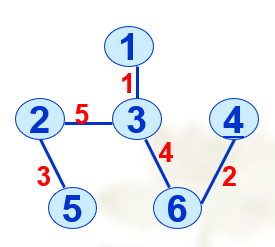
详细代码

/**
  * 构建最小生成树，求得最短路径
  * @param sMap 图
  * @param first 开始构建树时加入的第一个结点
  * @return 最短路径
  */
 public int createMinProTree(SimpleMap sMap,int first) {
  	//构建一个数组，用于存储当前图到其他结点的最小权值
  	int[] minInfo = new int[sMap.num];
  	int lenghth = 0;
  	//初始化数组(从1(数组中索引为0)开始构建)
  	System.out.println("加入顶点："+first);
  	for(int i=0; i<sMap.num; i++) {
   		//第一列存储最小权值
   		minInfo[i] = sMap.map[first-1][i];   
  	}
  	//最小生成树中顶点数
  	int number = 1;
  	while(number < 6) {
   		//遍历当前数组，找到距离最短的路径对应的顶点加入
   		int minValue = CreateAMap.MAX;
   		int index = 0;
   		for(int i=0; i<sMap.num; i++) {
   			 if(minInfo[i] !=0 && minValue > minInfo[i]) {
     				minValue = minInfo[i];
     				index = i;
    			}
   		}
   		//将index对应的顶点加入树中，更新树中数据(保持其他顶点到树的距离最短）
   		System.out.println("加入顶点："+(index+1));
   		lenghth += minValue;
   		minInfo[index] = 0;
   		for(int i=0; i<sMap.num; i++) {
    			if(minInfo[i] > sMap.map[index][i]) {
     				minInfo[i] = sMap.map[index][i];
    			}
   		} 
   		number++;
  	}  
  	return lenghth;
 }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

结果图