深度学习中常用计算距离的几种算法对比与python实现

前言

距离度量在许多机器学习算法中扮演着至关重要的角色，无论是监督学习还是无监督学习。选择适当的距离度量可以显著影响模型的性能。

在高维数据集中，欧几里得距离可能会受到所谓的“维度诅咒”的影响，因为随着维度的增加，数据点之间的距离会变得稀疏，导致欧几里得距离失效。在这种情况下，可以考虑使用更适合高维数据的距离度量，比如余弦相似度或者基于稀疏矩阵的距离度量。

另一方面，如果数据包含地理空间信息，如经纬度坐标，哈弗斯坦（Haversine）距离可能会更合适，因为它考虑了地球曲面的形状，能够更准确地衡量地理空间位置之间的距离。

了解何时使用哪种距离度量是非常重要的，这需要对数据的特点以及所使用的算法有深入的理解。在选择距离度量时，需要考虑数据的特征、数据的分布、数据的维度以及算法的特性，以便得到更好的模型性能。

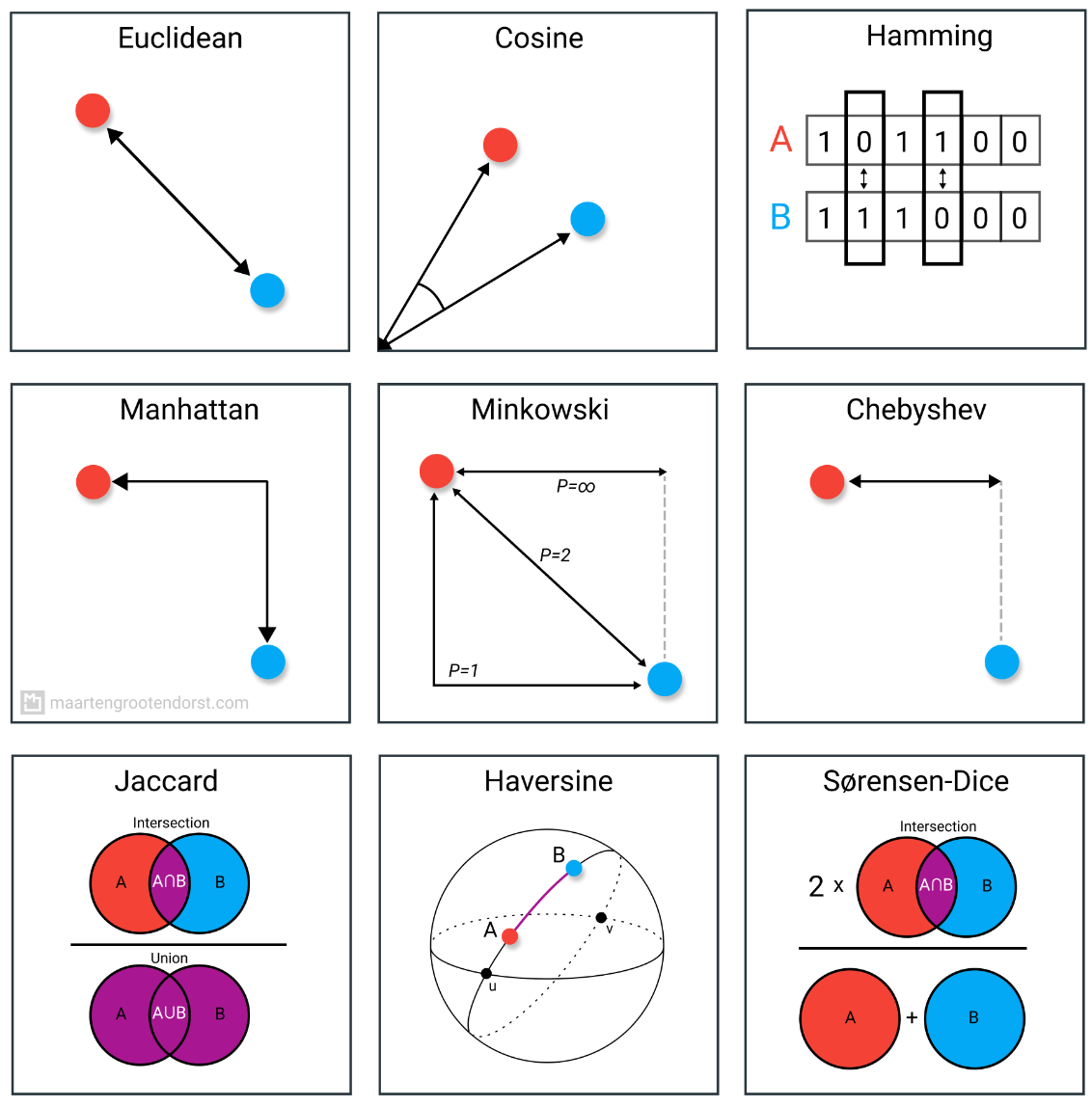
1. 欧氏距离

欧氏距离是最好的解释是连接两点之间的线段的长度。公式相当直接，因为距离是通过使用勾股定理计算点的笛卡尔坐标得到的。
$$D(x,y)=\sqrt{\sum _{i=1}^n(x_i-y_i{)}^2)}$$

劣势

尽管它是一种常见的距离度量，殴氏距离不是尺度不变的，这意味着计算出的距离可能会因特征的单位而产生偏差。通常，在使用这种距离度量之前需要对数据进行归一化。

此外，随着数据维度的增加，欧几里得距离变得越不有用。这与维度的诅咒有关，它涉及到高维空间并不像在2维或3维空间中直观预期的那样行动的概念。

用例

当拥有低维数据且向量的大小对测量很重要时，欧氏距离效果很好。如果在使用低维数据的kNN和HDBSCAN上使用欧几里得距离，方法会立即显示出很好的结果。

尽管已经开发了许多其他度量来弥补欧几里得距离的劣势，但由于使用它有很好的理由，它仍然是最常用的距离度量之一。它非常直观易用，简单易实现，并且在许多用例中显示出很好的结果。

Python示例

import numpy as np

def euclidean_distance(point1, point2):
    """
    计算两点之间的欧氏距离
    
    参数：
    point1: 第一个点的坐标，例如 [x1, y1, z1, ...]
    point2: 第二个点的坐标，例如 [x2, y2, z2, ...]
    
    返回值：
    两点之间的欧氏距离
    """
    point1 = np.array(point1)
    point2 = np.array(point2)
    distance = np.linalg.norm(point1 - point2)
    return distance

# 示例
point1 = [1, 2, 3]
point2 = [4, 5, 6]
distance = euclidean_distance(point1, point2)
print("两点之间的欧氏距离为:", distance)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

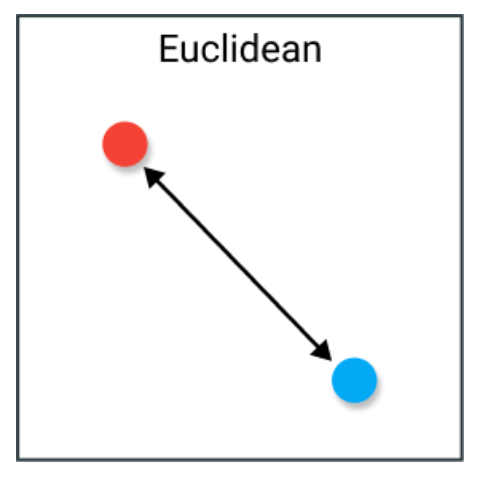
2. 余弦相似度

余弦相似度经常被用来解决欧几里得距离在高维性问题上的问题。余弦相似度简单地说是两个向量之间夹角的余弦。它也有向量归一化后相同内积的向量。

两个方向完全相同的向量具有余弦相似度为1，而两个完全相反的向量具有相似度为-1。请注意，它们的幅度不重要，因为这是方向的度量。
$$D(x,y)=cos(\theta )=\frac{x\cdot y}{\left||x|\right|\left||y|\right|}$$

劣势

余弦相似度的一个主要劣势是不考虑向量的幅度，只考虑它们的方向。在实践中，这意味着差异值没有被完全考虑在内。如果以推荐系统为例，那么余弦相似度不考虑不同用户之间评分尺度的差异。

用例

当拥有高维数据且向量的幅度不重要时，经常使用余弦相似度。在文本分析中，当数据由词频表示时，这种度量经常被使用。例如，当一个词在一个文档中出现的频率比另一个文档高时，这并不一定意味着一个文档与那个词更相关。可能是文档长度不均匀，计数的幅度不那么重要。然后，最好使用余弦相似度，它不考虑幅度。

Python示例

import numpy as np

def cosine_similarity(vector1, vector2):
    """
    计算两个向量之间的余弦相似度
    
    参数：
    vector1: 第一个向量，例如 [x1, y1, z1, ...]
    vector2: 第二个向量，例如 [x2, y2, z2, ...]
    
    返回值：
    两个向量之间的余弦相似度
    """
    dot_product = np.dot(vector1, vector2)
    norm_vector1 = np.linalg.norm(vector1)
    norm_vector2 = np.linalg.norm(vector2)
    similarity = dot_product / (norm_vector1 * norm_vector2)
    return similarity

# 示例
vector1 = [1, 2, 3]
vector2 = [4, 5, 6]
similarity = cosine_similarity(vector1, vector2)
print("两个向量之间的余弦相似度为:", similarity)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

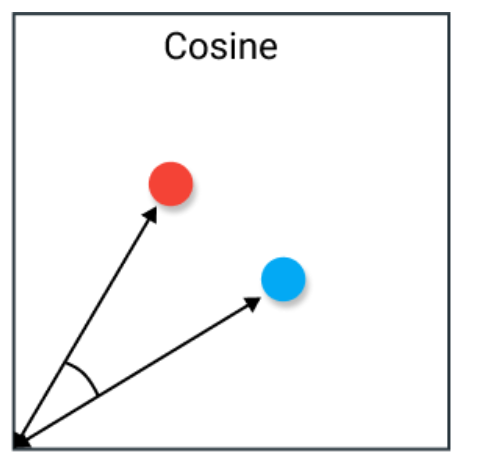
3. 汉明距离

汉明距离是两个向量之间不同值的数量。它通常用于比较两个等长的二进制字符串。它也可以用来比较字符串，通过计算彼此不同的字符数量来衡量它们之间的相似性。

劣势

当出现两个向量长度不相等时，汉明距离很难使用。理想的状态希望比较两个行长的向量，以便了解哪些位置不匹配。因此，当幅度是一个重要的度量时，不建议使用汉明距离度量。

用例

典型的用例包括在计算机网络传输数据时的错误校正/检测。它可以用来确定二进制词中扭曲的位数，作为估计错误的一个方法。此外，还可以使用汉明距离来衡量分类变量之间的距离。

Python示例

def hamming_distance(string1, string2):
    """
    计算两个等长字符串之间的汉明距离
    
    参数：
    string1: 第一个字符串
    string2: 第二个字符串
    
    返回值：
    两个字符串之间的汉明距离
    """
    if len(string1) != len(string2):
        raise ValueError("字符串长度不相等")
    
    distance = 0
    for char1, char2 in zip(string1, string2):
        if char1 != char2:
            distance += 1
    
    return distance

# 示例
string1 = "101010"
string2 = "111000"
distance = hamming_distance(string1, string2)
print("两个字符串之间的汉明距离为:", distance)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

4. 曼哈顿距离

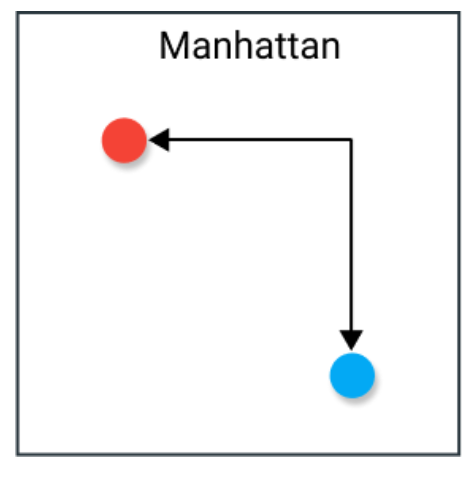
曼哈顿距离是计算实值向量之间的距离。想象一下描述棋盘上物体的向量。那么曼哈顿距离指的是两个向量之间的距离，如果它们只能直角移动。在计算距离时不涉及对角线移动。
$$D(x,y)=\sum _{i=1}^k|x_i-y_i|$$

劣势

尽管曼哈顿距离似乎对高维数据工作得很好，但它是一种比欧氏距离不太直观的度量，特别是在高维数据中使用时。此外，它比氏更有可能给出更高的距离值，因为它不采取最短路径。这不一定会引起问题，但这是应该考虑的事情。

用例

当数据集具有离散和/或二元属性时，曼哈顿似乎效果很好，因为它考虑了在这些属性的值内实际可能采取的路径。以欧氏距离为例，当两个向量之间画一条直线时，在现实中这可能并不可能。

Python示例

def manhattan_distance(point1, point2):
    """
    计算两点之间的曼哈顿距离
    
    参数：
    point1: 第一个点的坐标，例如 [x1, y1]
    point2: 第二个点的坐标，例如 [x2, y2]
    
    返回值：
    两点之间的曼哈顿距离
    """
    if len(point1) != len(point2):
        raise ValueError("点的维度不相等")
    
    distance = sum(abs(x1 - x2) for x1, x2 in zip(point1, point2))
    return distance

# 示例
point1 = [1, 2]
point2 = [4, 6]
distance = manhattan_distance(point1, point2)
print("两点之间的曼哈顿距离为:", distance)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

5. 切比雪夫距离

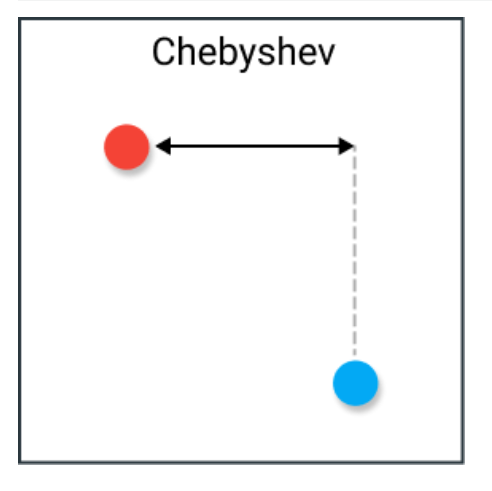
切比雪夫距离被定义为两个向量在任何坐标维度上的差异的最大值。换句话说，它只是沿一个轴的最大距离。由于其性质，它通常被称为棋盘距离，因为国王从一个方格移动到另一个方格所需的最小步数等于切比雪夫距离。

劣势

切比雪夫通常用于非常特定的用例，这使得它难以像欧氏距离或余弦相似度那样用作通用距离度量。因此，只有在绝对确定它适合你的例时，才建议使用它。

用例

如前所述，切比雪夫距离可以用来提取国王从一个方格移动到另一个方格所需的最小步数。此外，它在允许无限制8向移动的游戏中可能是一个有用的度量。实际上，切比雪夫距离通常用于仓库物流，因为它与吊车移动物体所需的时间非常相似。

Python示例

def chebyshev_distance(point1, point2):
    """
    计算两点之间的切比雪夫距离
    
    参数：
    point1: 第一个点的坐标，例如 [x1, y1]
    point2: 第二个点的坐标，例如 [x2, y2]
    
    返回值：
    两点之间的切比雪夫距离
    """
    if len(point1) != len(point2):
        raise ValueError("点的维度不相等")
    
    distance = max(abs(x1 - x2) for x1, x2 in zip(point1, point2))
    return distance

# 示例
point1 = [1, 2]
point2 = [4, 6]
distance = chebyshev_distance(point1, point2)
print("两点之间的切比雪夫距离为:", distance)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

6. 闵可夫斯基距离

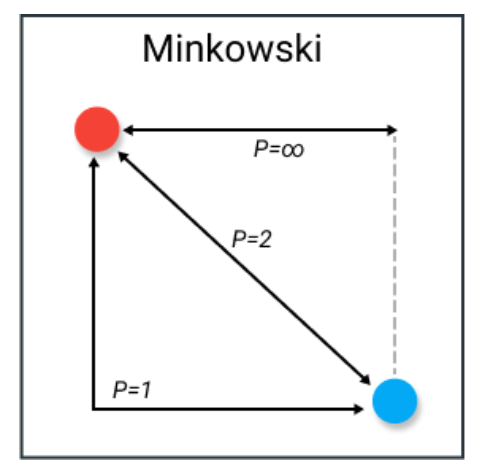
闵可夫斯基距离比大多数度量更为复杂。它是一个在范数向量空间（n维实数空间）中使用的度量，这意味着它可以在一个可以表示为具有长度的向量的空间中使用。

这个度量有三个要求：

• 零向量 —— 零向量的长度为零，而其他每个向量的长度都为正。例如，如果从一个地方到另一个地方，那么这个距离总是正的。然而，如果从一个地方到它自己，那么这个距离是零。

• 标量因子 —— 当你将向量乘以一个正数时，它的长度会改变，同时保持其方向。例如，如果我们在一个方向上走一定的距离，然后加上相同的距离，方向不会改变。

• 三角不等式 —— 两点之间最短的距离是一条直线。

闵可夫斯基距离的公式如下：
$$D(x,y)={\left(\sum _{i=1}^n{\left|x_i-y_i\right|}^p\right)}^{\frac{1}{p}}$$

最有趣的是这个度量中参数p的使用。我们可以使用这个参数来调整距离度量，使其密切类似于其他度量。

p的常见值是：

• p=1 — 曼哈顿距离

• p=2 — 欧几里得距离

• p=∞ — 切比雪夫距离

劣势

闵可夫斯基具有它们所代表的距离度量的相同劣势，因此非常好地理解像曼哈顿、欧氏和切比雪夫这样的度量是非常重要的。此外，参数p实际上可能很难处理，因为根据用例找到正确的值可能在计算上效率低下。

用例

p的优点是可以迭代它并找到最适合用例的距离度量。如果对p和许多距离度量非常熟悉，它允许你在距离度量上拥有巨大的灵活性，这可能是一个巨大的好处。

Python示例

import numpy as np

def minkowski_distance(point1, point2, p):
    """
    计算两点之间的闵可夫斯基距离
    
    参数：
    point1: 第一个点的坐标，例如 [x1, y1]
    point2: 第二个点的坐标，例如 [x2, y2]
    p: 距离的参数
    
    返回值：
    两点之间的闵可夫斯基距离
    """
    if len(point1) != len(point2):
        raise ValueError("点的维度不相等")
    
    distance = np.power(np.sum(np.power(np.abs(np.array(point1) - np.array(point2)), p)), 1/p)
    return distance

# 示例
point1 = [1, 2]
point2 = [4, 6]
p = 2
distance = minkowski_distance(point1, point2, p)
print("两点之间的闵可夫斯基距离为:", distance)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

7. 杰卡德系数

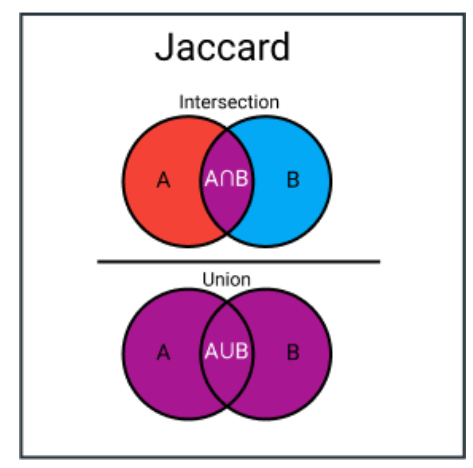
杰卡德指数（或并集上的交集）是用于计算样本集的相似性和多样性的度量。它是交集的大小除以并集的大小。在实践中，它是集合之间相似实体的总数除以实体的总数。例如，如果两个集合有1个共同实体和总共5个不同的实体，那么杰卡德指数将是1/5 = 0.2。

要计算杰卡德距离，我们只需从1中减去杰卡德指数：
$$D(x,y)=1-\frac{\left|x\cap y\right|}{\left|y\cup x\right|}$$

劣势

杰卡德指数的一个主要劣势是它受数据大小的影响很大。大型数据集可能会对指数产生很大影响，因为它可能会显著增加并集，同时保持交集相似。

用例

杰卡德指数通常用于二元或二值化数据的应用程序。例如，当有一个深度学习模型预测图像的某个部分，例如l图像中的汽车时，杰卡德指数可以用来计算给定真实标签的预测部分的准确性。同样，它可以用于文本相似性分析，以衡量文档之间有多少单词选择重叠。因此，它可以用于比较模式集。

Python示例

def jaccard_coefficient(set1, set2):
    """
    计算两个集合之间的杰卡德系数
    
    参数：
    set1: 第一个集合，例如 {element1, element2, ...}
    set2: 第二个集合，例如 {element3, element4, ...}
    
    返回值：
    两个集合之间的杰卡德系数
    """
    intersection = len(set1.intersection(set2))
    union = len(set1.union(set2))
    coefficient = intersection / union
    return coefficient

# 示例
set1 = {1, 2, 3}
set2 = {2, 3, 4}
jaccard_coeff = jaccard_coefficient(set1, set2)
print("两个集合之间的杰卡德系数为:", jaccard_coeff)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

8.哈弗辛距离

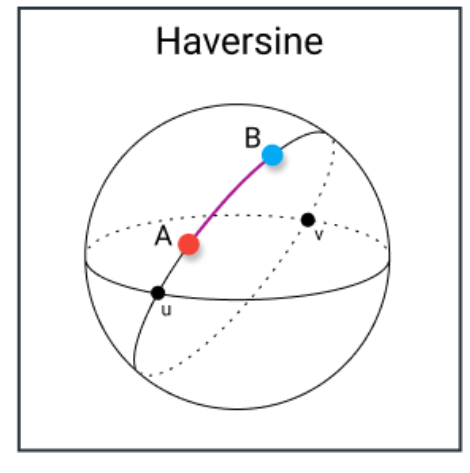
哈弗辛距离是基于两点的经度和纬度计算球体表面上的距离。它与欧几里得距离非常相似，因为它计算的是两点之间的最短直线。主要的区别在于，这里假设的两点位于球体上，因此不存在直线路径。
$$d=2rarcsin\left(\sqrt{si{n}^2\left(\frac{{\phi }_2-{\phi }_1}{2}\right)+cos({\phi }_1)cos({\phi }_2)si{n}^2\left(\frac{{\lambda }_2-{\lambda }_1}{2}\right)}\right)$$

劣势

这种距离度量的一个缺点是它假设点位于球体上。实际上，这种情况很少见，例如，地球并不是完美的圆形，这可能使得在某些情况下的计算变得困难。相反，值得关注的是文森特距离（Vincenty distance），它假设的是椭球体而非球体。

用例

哈弗辛距离经常用于导航。例如，可以使用它来计算两个国家之间的飞行距离。需要注意的是，如果本身距离不是很远，它就不那么适用。在这种情况下，曲率的影响不会那么大。

Python示例

import math

def haversine(lat1, lon1, lat2, lon2):
    """
    计算地球上两点之间的哈弗辛距离
    
    参数：
    lat1: 第一个点的纬度
    lon1: 第一个点的经度
    lat2: 第二个点的纬度
    lon2: 第二个点的经度
    
    返回值：
    两点之间的哈弗辛距离（单位为千米）
    """
    # 将经度和纬度转换为弧度
    lat1_rad = math.radians(lat1)
    lon1_rad = math.radians(lon1)
    lat2_rad = math.radians(lat2)
    lon2_rad = math.radians(lon2)
    
    # 使用哈弗辛公式计算距离
    dlon = lon2_rad - lon1_rad
    dlat = lat2_rad - lat1_rad
    a = math.sin(dlat / 2) ** 2 + math.cos(lat1_rad) * math.cos(lat2_rad) * math.sin(dlon / 2) ** 2
    c = 2 * math.atan2(math.sqrt(a), math.sqrt(1 - a))
    radius_of_earth = 6371  # 地球的半径，单位为千米
    distance = radius_of_earth * c
    
    return distance

# 示例
latitude1 = 52.2296756
longitude1 = 21.0122287
latitude2 = 52.406374
longitude2 = 16.9251681
distance = haversine(latitude1, longitude1, latitude2, longitude2)
print("两点之间的哈弗辛距离为:", distance, "千米")

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

9. 索伦森-戴斯指数

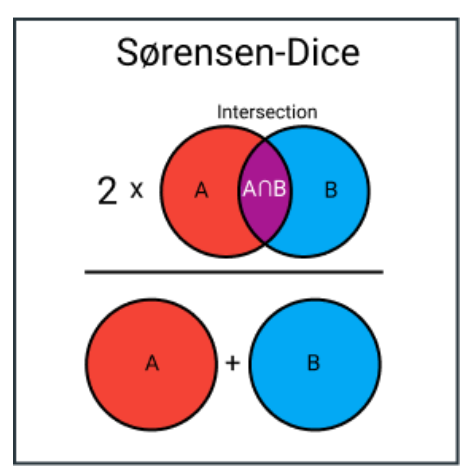
索伦森-戴斯指数与杰卡德指数非常相似，它用于衡量样本集的相似性和多样性。尽管它们的计算方式相似，但索伦森-戴斯指数更为直观，因为它可以被视为两集合之间重叠的百分比，这是一个介于0和1之间的值。

劣势

与杰卡德指数一样，这两种指数都过分强调了那些几乎没有或根本没有真实正集的集合的重要性。结果，它可能会主导在多个集合上取平均分的情况。它将每个项目的重要性与相关集合的大小成反比，而不是平等对待。

用例

索伦森-戴斯指数的用例与杰卡德指数相似，如果不是完全相同的话。你通常会在图像分割任务或文本相似性分析中发现它被使用。

Python示例

def sorensen_dice_coefficient(set1, set2):
    """
    计算两个集合之间的索伦森-戴斯指数
    
    参数：
    set1: 第一个集合，例如 {element1, element2, ...}
    set2: 第二个集合，例如 {element3, element4, ...}
    
    返回值：
    两个集合之间的索伦森-戴斯指数
    """
    intersection = len(set1.intersection(set2))
    total_elements = len(set1) + len(set2)
    coefficient = 2 * intersection / total_elements
    return coefficient

# 示例
set1 = {1, 2, 3}
set2 = {2, 3, 4}
sorensen_dice = sorensen_dice_coefficient(set1, set2)
print("两个集合之间的索伦森-戴斯指数为:", sorensen_dice)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22