离散卡尔曼滤波器算法详解及重要参数(Q、R、P)的讨论_卡尔曼滤波 pqgr

1. 公开数据集中文版详细描述参考前文：https://editor.csdn.net/md/?not_checkout=1&spm=1011.2124.3001.6192
2. 神经元Spike信号分析参考前文：https://blog.csdn.net/qq_43811536/article/details/134359566?spm=1001.2014.3001.5501
3. 神经元运动调制分析参考前文：https://blog.csdn.net/qq_43811536/article/details/134401004?spm=1001.2014.3001.5501

---

---

摘要

1960年，卡尔曼发表了他著名的用递归方法解决离散数据线性滤波问题的论文。从那以后，得益于数字计算技术的进步，卡尔曼滤波器已成为推广研究和应用的主题，尤其是在自主或协助导航领域。

卡尔曼滤波器由一系列递归数学公式描述。它们提供了一种高效可计算的方法来估计过程的状态，并使估计均方误差最小。卡尔曼滤波器应用广泛且功能强大：它可以估计信号的过去和当前状态，甚至能估计将来的状态，即使并不知道模型的确切性质。

本文简单介绍了离散卡尔曼滤波器（以下简称“KF”）的计算理论，同时基于猕猴感觉运动皮层神经元的运动解码分析讨论KF的三个重要参数Q、R、P对算法的影响。

---

1. 离散卡尔曼滤波器算法

1.1 理论概述

卡尔曼滤波器用反馈控制的方法估计过程状态：滤波器估计过程某一时刻的状态，然后以（含噪声的）测量变量的方式获得反馈。因此卡尔曼滤波器可分为两个部分：时间更新方程和测量更新方程。时间更新方程负责及时向前推算当前状态变量和误差协方差估计的值，以便为下一个时间状态构造先验估计。测量更新方程负责反馈——也就是说，它将先验估计和新的测量变量结合以构造改进的后验估计。

1.2 算法细节

• 时间更新方程也可视为预估方程，测量更新方程可视为校正方程，分别对应 Figure 1中的“时间更新（预测）”和“测量更新（校正）”。最后的估计算法成为一种具有数值解的预估－校正算法。

• 实际系统中，过程激励噪声协方差矩阵 Q 和观测噪声协方差矩阵 R 可能会随每次迭代计算而变化。但在这儿我们假设它们是常数。

• 测量更新方程首先做的是计算卡尔曼增益 $K_k$，其次便测量输出以获得 $z_k$ ，然后按（2）式产生状态的后验估计。最后按（3）式估计状态的后验协方差。

• 计算完时间更新方程和测量更新方程，整个过程再次重复。上一次计算得到的后验估计被作为下一次计算的先验估计。这种递归推算是卡尔曼滤波器最吸引人的特性之一——它比其它滤波器更容易实现：例如维纳滤波器¹ ，每次估计必须直接计算全部数据，而卡尔曼滤波器每次只根据以前的测量变量递归计算当前的状态估计。
  

Figure 1. 卡尔曼滤波器工作原理图

---

2. 神经元的运动解码分析

2.1 公开数据集

• 网址：Nonhuman Primate Reaching with Multichannel Sensorimotor Cortex Electrophysiology ²
• Session：
  • " indy_20170124_01 "

2.2 Q、R、P 的定义及初值设置

• Q：Q矩阵表示系统模型中过程噪声的协方差矩阵。它描述了系统状态在时间上的变化和不确定性。通常情况下，Q矩阵的初始值可以根据系统的动态范围和预期的噪声水平进行估计。本实验中Q的初始值为卡尔曼滤波器训练过程中转移矩阵的协方差。
• R：R矩阵表示测量模型中观测噪声的协方差矩阵。它描述了观测值和系统真实状态之间的不一致性或不确定性。R矩阵的初始值可以通过对测量数据进行统计分析来估计。本实验中R的初始值为卡尔曼滤波器训练过程中观测数据（测量矩阵）的协方差。
• P：P矩阵表示状态估计的协方差矩阵，它描述了状态估计和真实状态之间的不确定性。P矩阵的初始值可以根据系统的初始状态估计精度进行设置。本实验中P的初始值为零矩阵，表示对初始状态估计的高置信度。

2.3 KF 的解码结果

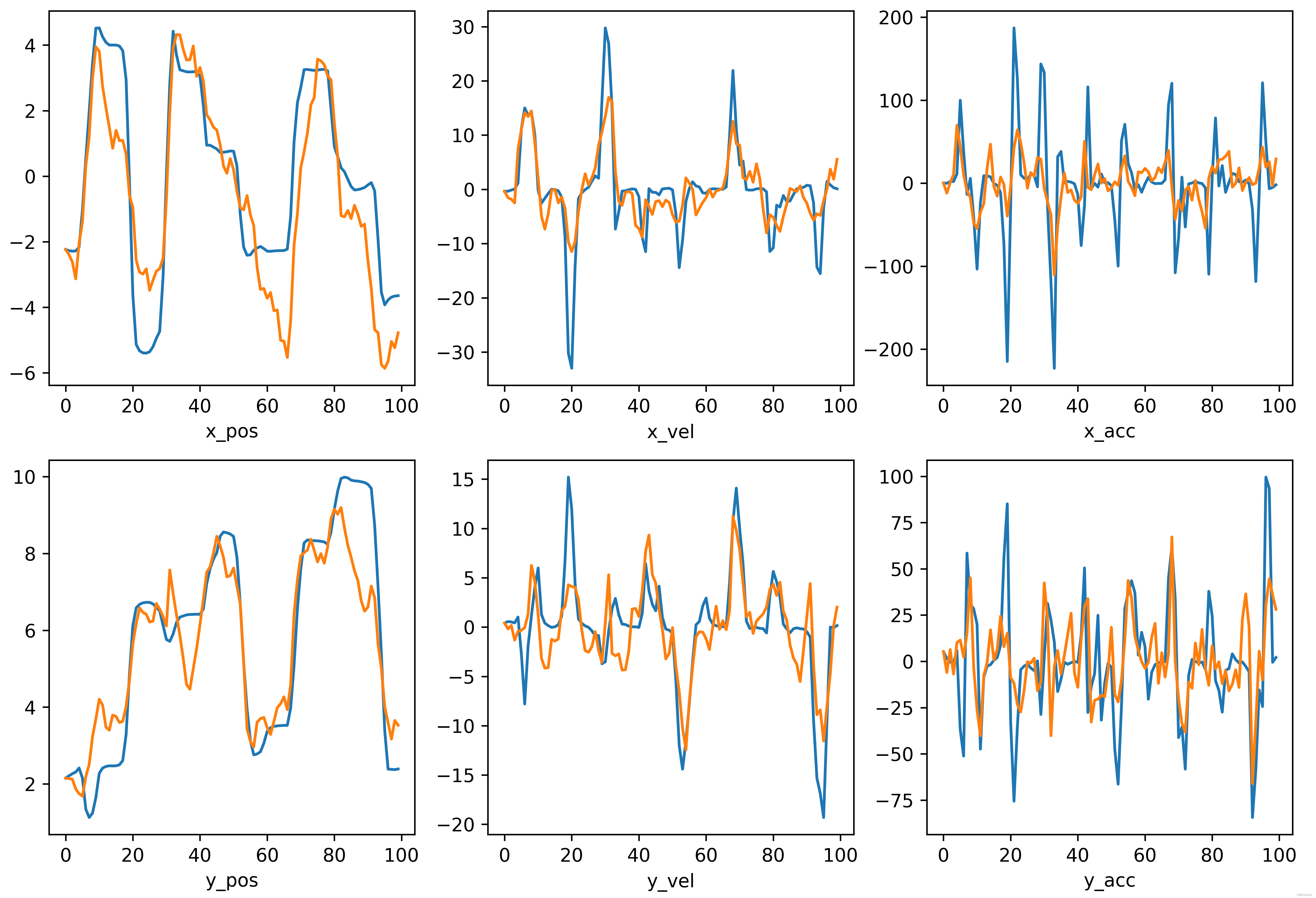
使用2.2节中 Q、R、P 的初始值设置卡尔曼滤波器对公开数据集" indy_20170124_01 "进行解码，并采用十折交叉验证进行评估，Figure 2 为第4折上前100个样本的真实（蓝色）和预测（黄色）曲线，上下分别代表x和y方向上的位置、速度和加速度。

Figure 2. 卡尔曼滤波器的部分解码结果

2.4 不同Q、R、P 初始值对计算结果的影响

Figure 3 展示了Q、R、P分别为上一节默认取值（Figure 3a）和高斯噪声（Figure 3b-d）时的部分解码结果，每一个子图从左到右由十折交叉验证中的第1、5、10折组成。可以看到R的取值对结果影响最大，只要不合理就会导致预测结果无意义；而P的取值影响最小，预测结果仅在前几个sample上会出现较大幅度的波动。

Figure 3. 不同Q、R、P 初始值的部分计算结果. a. 采用上一节的默认初始值. b. 将Q设置为均值为0，方差为100的高斯噪声. c. 将R设置为均值为0，方差为100的高斯噪声. d. 将P设置为均值为0，方差为100的高斯噪声.

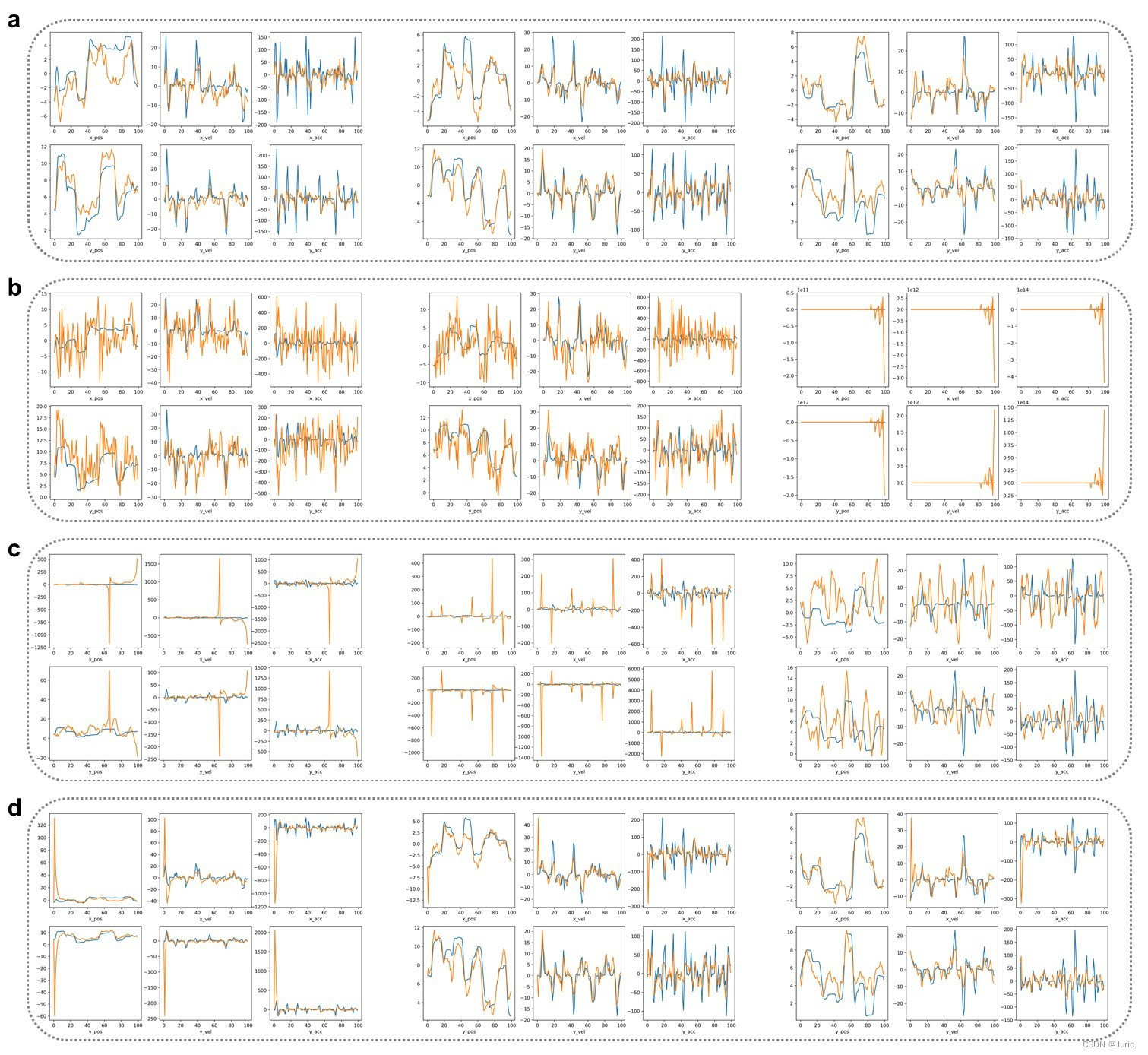
Table 1 记录了设置不同Q、R、P 初始值时卡尔曼滤波器的解码性能，其中$diag(n)$代表对角元素为n的对角矩阵。这些结果进一步证明上一段的结论，同时P设置为对角矩阵时可以最大程度地保持解码器的性能。

Table 1. 不同Q、R、P 初始值的解码性能

---

创作不易，麻烦点点赞和关注咯！

---

1. Brown, R. G. and P. Y. C. Hwang. 1992. Introduction to Random Signals and Applied Kalman Filtering, Second Edition, John Wiley & Sons, Inc. ↩︎

2. Makin, J. G., O’Doherty, J. E., Cardoso, M. M. B. & Sabes, P. N. (2018). Superior arm-movement decoding from cortex with a new, unsupervised-learning algorithm. J Neural Eng. 15(2): 026010. doi:10.1088/1741-2552/aa9e95 ↩︎