z=xy为什么是马鞍面？

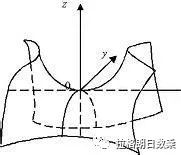
（马鞍面）

在高数2（同济大学版本）空间曲面中，我们在课后习题中会发现一个奇怪的方程：z=xy. 这个方程的形式似乎和我们学习到的各种空间曲面方程的形式都不沾边，但事实上，它是一个双曲抛物面（马鞍面）的形状，也就是说，它只是一个双曲抛物面的特殊情况。那么z=xy的方程是怎样得到的呢？

下面是它的简要推导过程（选自百度百科）：

看这个推导过程，可能还是有点懵逼，尤其是已经好久没碰高数的同学。接下来是较为具体的诠释。

既然是双曲抛物面，那么我们来回忆一下双曲抛物面是怎么来的。双曲抛物面，光看前俩字，是不是觉得它和双曲线有关系？事实上，它和双曲线无关，由二维双曲线推导出来的是旋转单叶双曲面与旋转双叶双曲面（简称旋转法） 而双曲抛物面是由截痕法得到的，而且是与二维抛物线有关。这一点，要看后面三个字。

（同济大学高等数学）

也就是说，你可以这样理解，先写了一个方程：z=x^2/a^2+y^2/b^2  然后用x=t去截 就会得到一个个开口向下的抛物线，随着x=t不断变化，顶点坐标变化，两端看着越来越大，形成一个马鞍的形状。

第二步顺着+z方向旋转45度就需要坐标变换了，这里 x=a*cos45-b*sin45 y=a*sin45+b*cos45 代表 空间坐标系 Z轴不变 X,Y轴同时旋转 45度 

为了消去xy前面的系数，令a=√2，就得到了这样的形式：z=xy. ①若将√2带入最初双曲抛物面方程，就得到了

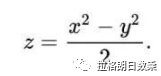
②

①与②是全等的。有些同学会说，令x=2,y=2,两个方程得到的z的值都不同，怎么可能全等？因为这里指的是形状大小

​利用坐标旋转便知它是马鞍面：令x=(u+v)/√2,y=(u-v)/√2,z=z,方程变作:z=½(u²-v²),这就是马鞍面

​

（懂的都懂吧）

拉格朗日数乘

欢迎来到理工科的世界

公众号

​​