机器学习之朴素贝叶斯法及其python实现_朴素贝叶斯python

写在前面

本文主要是学习记录贴，参考《统计学习方法》和部分博客完成。如有错误，欢迎积极评论指出。

背景介绍

首先，简单讲一下机器学习中的两大学派——频率学派和贝叶斯派。

频率派

频率派认为世界是确定的，即θ（表示需要求的事件）存在唯一的真值，并且这个真值是不变的，我们的目标就是找到这个真值或者说这个真值存在的范围。用个例子来说明，我们在学概统时，常说投硬币，如果我们现在投硬币100次，出现正面朝上的概率是40，那么我们用θ表示硬币正面朝上，则p(θ) = 40 / 100 = 0.4。当数据量趋于无穷大的时候，这种方法能给出准确的估计。但是在缺乏数据的时候，就可能存在很大的误差。比如现在我们投10次硬币，全部都是正面朝上的，这是我们认为正面朝上的概率就是1，这在我们的认知中，是肯定错误的。

贝叶斯派

贝叶斯派认为世界是不确定的，人们应该提前有个先验，然后通过观测数据，对这个先验进行调整，然后找到最优的用于描述这个世界的概率分布。在贝叶斯派中，有两大输入和一大输出。两大输入是先验和似然，输出的是后验。先验，p(θ)指的是在没有观察到数据时对θ的预先判断，可以通过给定的训练样本进行统计得到的。似然，p(x|θ)是假设θ已知后我们观察到的数据应该是什么样，也是可以根据训练样本进行统计得到的。后验，p(θ|x)也就是我们最后需要求的值。

朴素贝叶斯法

朴素贝叶斯法的核心是贝叶斯公式，其工作原理是根据通过某种方法求该事件所有可能性的发生概率，然后哪个高就是哪个。那么，这种方法是什么？

基本概念

首先是贝叶斯公式，如下：
$$P(\theta |X)=\frac{P(X|\theta )\times P(\theta )}{P(X)}$$
公式中，$P(\theta )$表示先验概率，$P(X|\theta )$表示似然。
接下来，我们针对实际应用中，定义几个变量。首先Ck 表示不同的类，X表示给定的样本，Y表示Ck的概率。公式变换如下：

对于上面公式变换，可能会存在一个疑问，那就是为什么可以将里面的拆开成连乘？我们在概率论中，这个公式的使用是有前提条件的，也就是相互独立。那么这里面，是条件独立吗？事实上，特征向量之间大概率不是独立的，但是我们默认特征之间是独立的，最主要的原因就是简便计算。如果我们考虑其特征向量之间的联系，会使模型变得非常复杂，容易造成过拟合。所以我们就假设所有的特征向量都是相互独立的。

最后我们得到了如下公式：

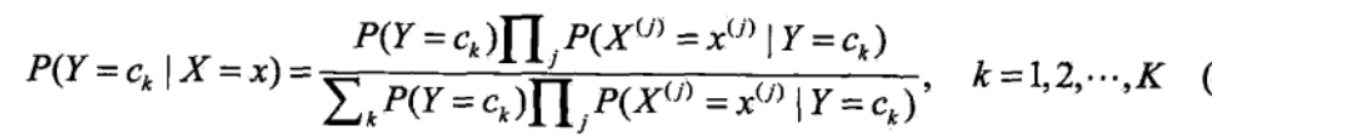
针对上面上面的公式，我们会发现，对同一组训练数据，其分母部分是相同的。我们最后的目的，是要找出最大的那个类，因此，这一部分不影响大小比较，接着简化公式。

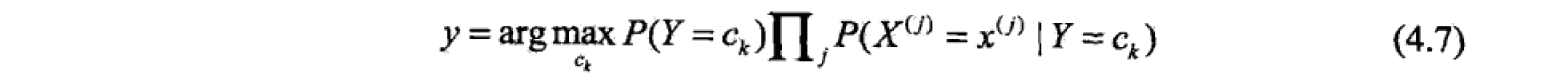
参数估计

在朴素贝叶斯法中，学习意味着对于参数P(Y=Ck) 和 P(X=x|Y=Ck)进行估计。常用的方法是利用极大似然估计，估计如下：

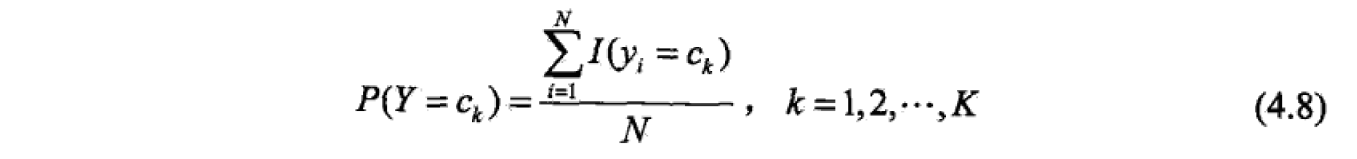
学习与分类算法

构建学习与分类算法如下：

贝叶斯估计

对于上面的算法，因为其中出现了连乘，那么就需要考虑，零的问题了。

在利用极大似然进行估计的时候，可能会出现某个值为0，那么在进行后续连乘计算的时候，就会出现问题，导致分类产生偏差。解决这个问题的一个方法就是采用贝叶斯估计。条件概率的贝叶斯估计如下：

其中，λ=0时，就是极大似然估计。常取λ=1，称为拉普拉斯平滑，其中S表示该项特征的可能取值。

python实现

import numpy as np

# 读取数据，将图片读取为785维的向量，其中前784维是28*28，最后是标签
def LoadData(filename):
    data = []
    i = 0
    file = open(filename)
    for line in file.readlines():
        curline = line.strip().split(',')
        data.append([int(int(dt) > 128) for dt in curline[1:]])   #二值化
        data[i].append(int(curline[0]))
        i += 1
    return data

# 计算似然和先验
def calProbability(trainData):
    featurenum = len(trainData[0]) - 1
    P_y = [0] * 10      # 计算先验P(θ)，并存储
    for i in trainData:
        P_y[i[-1]] += 1
    for j in range(len(P_y)):
        P_y[j] = (P_y[j] + 1) / (len(trainData) + len(P_y))
    P_x_y = np.zeros((10, featurenum, 2))       # 计算似然P(x|θ)
    for i in trainData:
        for j in range(featurenum):
            P_x_y[i[-1]][j][i[j]] += 1
    for m in range(10):
        for n in range(featurenum):
            value0 = P_x_y[m][n][0]
            value1 = P_x_y[m][n][1]
            P_x_y[m][n][0] = (value0 + 1) / (value0 + value1 + 2)
            P_x_y[m][n][1] = (value1 + 1) / (value0 + value1 + 2)
    return P_y, P_x_y

# 通过朴素贝叶斯进行概率估计
# Data:测试数据
# P_y:先验
# P_x_y:似然
def Bayes(Data, P_y, P_x_y):
    predict = [0] * 10
    for i in range(10):
        p = P_y[i]
        for j in range(len(Data)):
            p = p * P_x_y[i][j][Data[j]]
        predict[i] = p
    return predict.index(max(predict))

# 测试函数
def test(testData, P_y, P_x_y):
    err = 0
    m = 0
    for i in testData:
        print('测试编号：', m)
        m += 1
        predict = Bayes(i[:-1], P_y, P_x_y)
        if predict != i[-1]:
            err += 1
    return 1 - (err / (len(testData)))


if __name__ == "__main__":   
    print('read train data')
    trainData = LoadData('Mnist/mnist_train/mnist_train.csv')

    print('read test data')
    testData = LoadData('Mnist/mnist_test/mnist_test.csv')

    print('start train model')
    P_y, P_x_y = calProbability(trainData)

    print('start test model')
    acc = test(testData, P_y, P_x_y)

    print('the acc is: ', acc)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74