数据结构——线性表（详细配代码讲解）_数据结构线性表代码怎么看

引言：

        线性表是一种非常基础和重要的数据结构，它由一系列有序的元素组成，每个元素最多只有一个前驱和一个后继（线性关系）。线性表在计算机科学和实际应用中都有着广泛的应用，比如在操作系统中实现进程调度、在数据库系统中管理数据等。因此，理解和掌握线性表的基本概念和操作非常重要。

在数据结构中，线性表是一种非常直观和容易理解的数据结构，它的操作也比较简单和直观。然而，在实际应用中，我们需要根据具体的问题和应用场景来选择合适的线性表实现方式，比如顺序存储结构或者链式存储结构等。同时，我们还需要针对具体的应用场景来设计和实现高效的算法和程序，以达到最优的处理效果和性能。

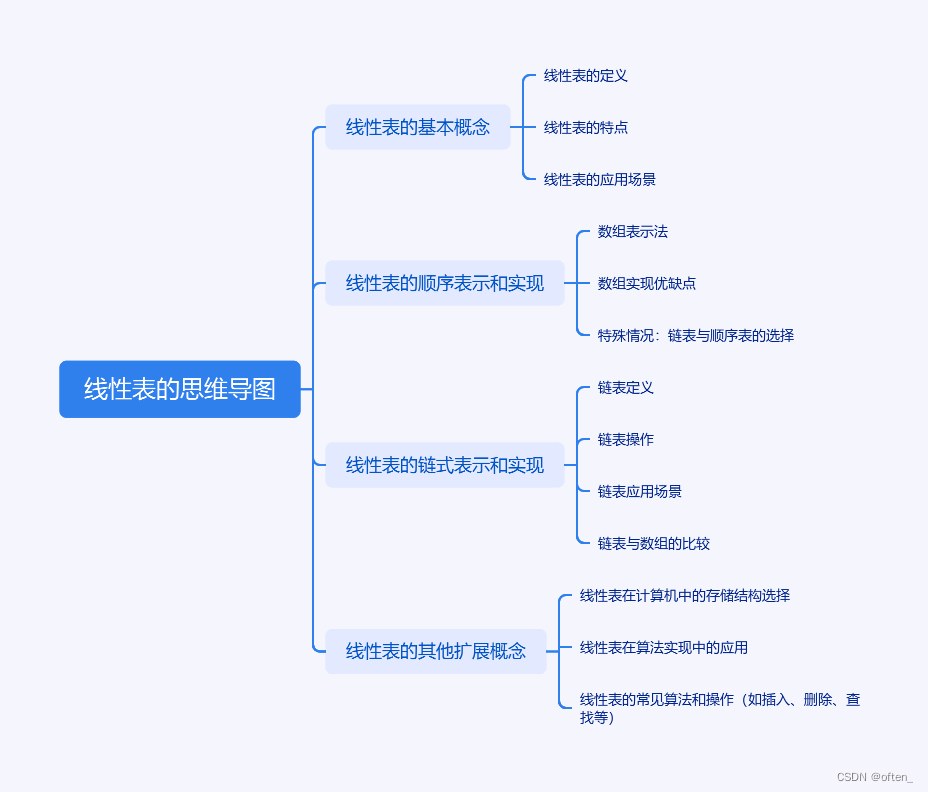
在这篇博客中，我们将从以下几个方面来探讨线性表：

1. 线性表的基本概念：介绍线性表的定义、特点和应用场景。
2. 线性表的顺序存储结构：讨论顺序存储结构的实现方法、优缺点以及适用场景。
3. 线性表的链式存储结构：讨论链式存储结构的实现方法、优缺点以及适用场景。
4. 线性表的主要操作：分别讨论顺序存储结构和链式存储结构下实现插入、删除、查找和修改操作的算法和时间复杂度。

线性表的定义：

线性表是一种具有相同特性的有限个元素的序列，每个元素都有一个前驱和一个后继，除了第一个元素之外，每个元素都有一个唯一的直接前驱，除了最后一个元素之外，每个元素都有一个唯一的直接后继。

线性表的特点：

        1.同一性：线性表由同类数据元素组成，每一个数据元素必须属于用一个数据对象。

        2.有穷性：线性表由有限个数据元素组成，表长度就是表中数据元素的个数。

        3.有序性：线性表中相邻的数据元素之间存在着序偶关系。（每个元素都有一个前驱和一个后继，除了第一个元素之外，每个元素都有一个唯一的直接前驱，除了最后一个元素之外，每个元素都有一个唯一的直接后继）

线性表的应用场景：

线性表在计算机科学和实际应用中都有着广泛的应用，比如在操作系统中实现进程调度、在数据库系统中管理数据等。此外，线性表还可以用于实现各种算法和数据结构，比如二叉树、堆等。

线性表的顺序存储结构

顺序存储结构实现方式：

        在程序中，可以定义一个数组来存储线性表的元素，数组的每个元素对应线性表中的一个元素。数组的长度即为线性表的长度。在访问线性表中的元素时，可以通过下标直接访问数组中的对应元素。
        

代码实现：

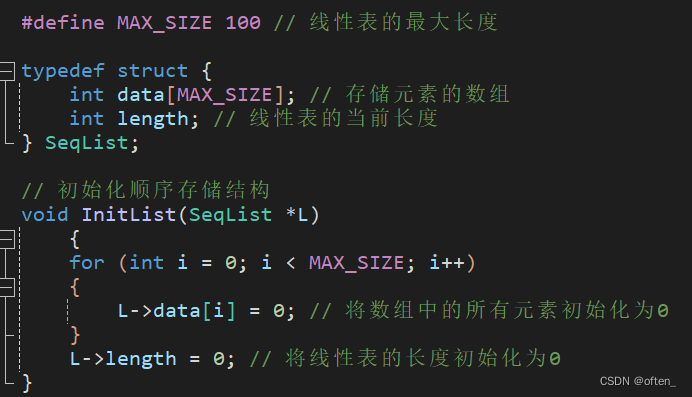
顺序存储结构优缺点：
优点：

        1.支持随机访问：顺序表中的元素可以通过下表进行快速访问，时间复杂度为O(1)。

        2.空间利用率高：顺序存储结构可以利用数组中未使用的空间来存储其他元素，因此可以高效地利用存储空间。

        3.访问速度快：由于元素是按照逻辑顺序排列的，可以直接通过下标访问任意一个元素，因此访问速度非常快。

缺点：

1. 插入和删除操作需要移动元素：当需要在顺序存储结构中插入或删除元素时，需要将该元素之后的所有元素向后或向前移动一定的位置，这会使得时间复杂度较高。

2. 长度不易动态调整：顺序存储结构在初始化时需要指定存储空间的大小，因此在需要动态调整线性表长度时需要重新分配存储空间，这会带来一定的开销和复杂性。

顺序存储结构使用场景：

1. 不需要频繁插入和删除操作的场景：如果线性表中的元素数量固定不变，或者不需要频繁进行插入和删除操作，那么顺序存储结构是一种很好的选择。例如，在某些特定的算法中，需要使用固定长度的缓冲区来处理数据，此时可以采用顺序存储结构来实现。

2. 对内存空间要求较高的场景：在一些对内存空间要求较高的场景中，顺序存储结构可以充分利用存储空间，减少内存空间的浪费。例如，在嵌入式系统和移动设备中，由于内存资源有限，通常会采用顺序存储结构来实现线性表。

线性表的链式存储结构

链式存储的实现方法：

        线性表的链式存储结构通常采用链表来实现。链表中的每个元素称为结点，每个结点包含两个部分：数据域和指针域。数据域用于存储元素的值，指针域用于存储指向下一个结点的指针。通过指针将各个结点链接起来，形成了一个链表。

        在链表中，每个结点除了自身数据域外，还有一个指向下一个结点的指针，因此链表的长度可以在运行时动态调整。当插入一个新元素时，只需要创建一个新的结点，并将其插入到链表的适当位置；当删除一个元素时，只需要将该结点从链表中移除即可。

代码实现：

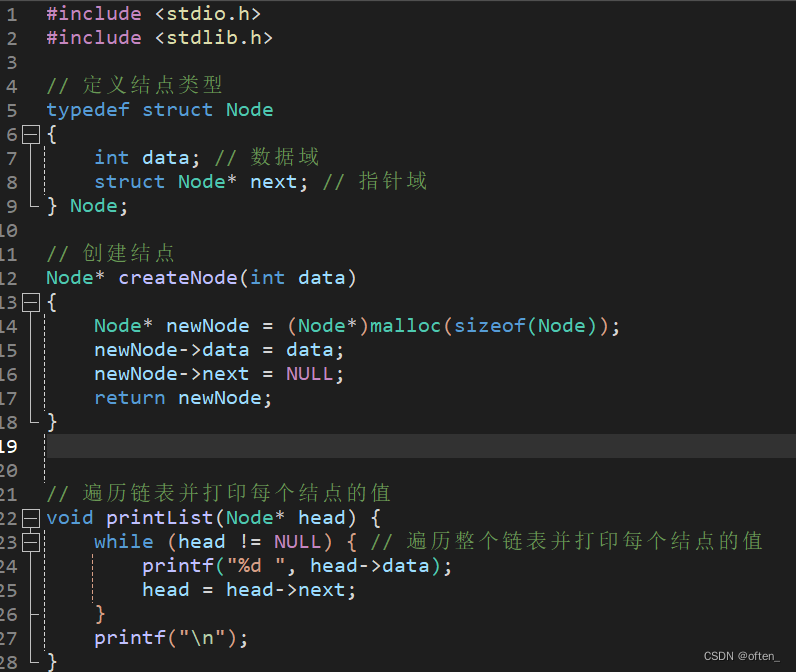
链式存储的优缺点：
优点：

1. 不需要连续的存储空间：链式存储结构中的元素可以分散存储，不需要像顺序存储结构那样需要一块连续的存储空间。

2. 插入和删除操作方便：链式存储结构中，插入和删除元素只需要修改指针即可，不需要移动其他元素。

3. 可以动态扩展：链式存储结构可以根据需要动态地增加或减少元素，方便灵活。

缺点：

1. 存储空间利用率低：链式存储结构中，每个结点除了存储数据外，还需要存储指向下一个结点的指针，因此存储空间利用率较低。

2. 访问元素速度慢：由于链式存储结构中的元素是分散存储的，因此不能像顺序存储结构那样直接通过下标访问元素，需要通过指针从头到尾遍历链表才能找到所需元素。

3. 需要额外的空间存储指针：链式存储结构需要额外的空间来存储指向下一个结点的指针。

链式存储的适用场景：

1. 需要频繁插入和删除操作的场景：对于需要频繁插入和删除操作的场景，采用链式存储结构可以避免顺序存储结构中移动元素的开销和时间复杂度。例如，在实现数据结构中的队列、栈等操作时，链式存储结构是一种常用的实现方式。

2. 对内存空间要求不高的场景：在一些对内存空间要求不高的场景中，采用链式存储结构可以充分利用其动态扩展的优点。例如，在实现文件系统时，可以使用链式存储结构来管理文件的数据块。

3. 需要实现动态数据结构的场景：对于需要实现动态数据结构的场景，如动态数组、动态树等，链式存储结构是一种常用的实现方式。通过动态地增加或减少元素，可以方便地实现数据结构的扩展和收缩。

线性表的主要操作

顺序表：

实现插入某个元素:

实现删除某个元素：

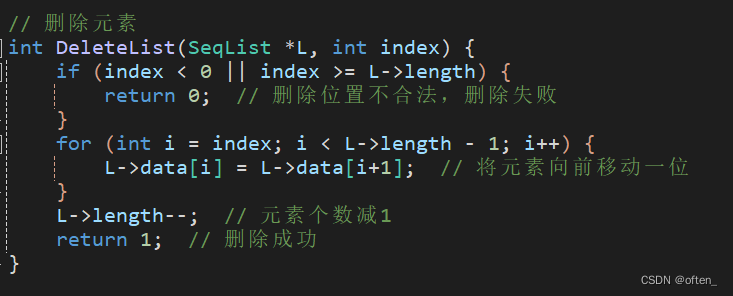
实现查找某个元素：

实现修改某个元素：

链式表：

实现插入某个元素：

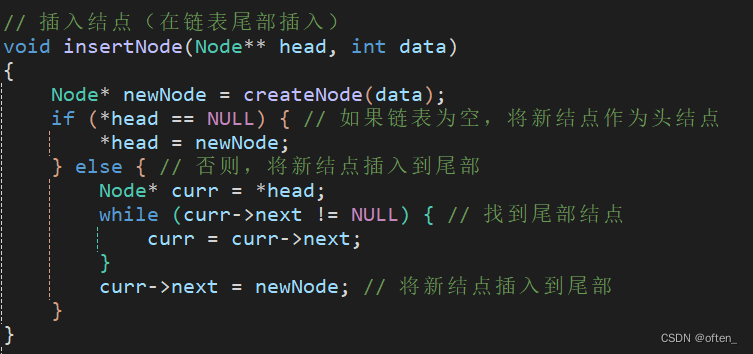
实现删除某个元素：

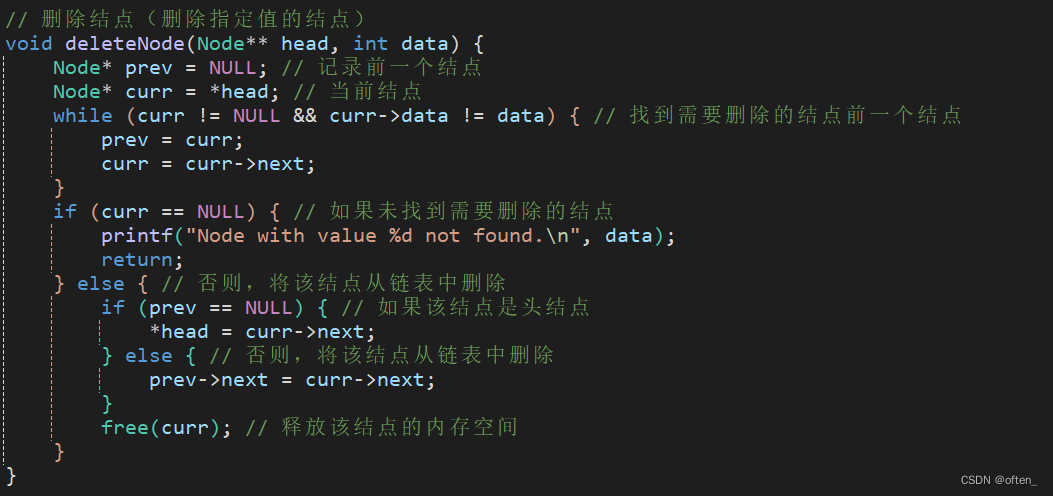
实现修改某个元素：

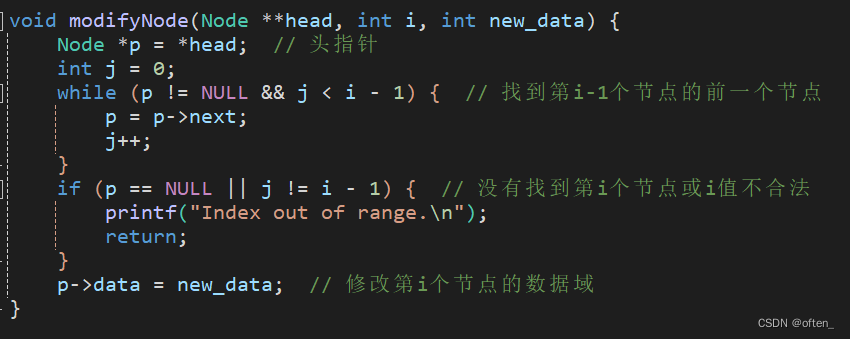
顺序存储的时间复杂度：

• 访问：顺序存储是连续的内存空间，可以通过计算直接访问任意位置的数据，时间复杂度为O(1)。

• 插入：顺序存储的插入操作通常需要移动元素来腾出空间，时间复杂度为O(n)，其中n是数据量。

• 删除：删除操作需要移动元素来填补空位，时间复杂度也为O(n)。

链式存储的时间复杂度：

• 访问：链式存储通过指针链接各个节点，访问任意位置的节点的时间复杂度为O(1)，因为只需通过指针直接访问。

• 插入：对于链表的插入操作，我们只需修改指针即可，不需要移动元素，时间复杂度为O(1)。

• 删除：删除操作只需修改指针，时间复杂度同样为O(1)。

以上便是线性表的基本概念、特点、应用场景、存储结构和代码实现的内容了。如果感兴趣的小伙伴可以使用线性表简单做一个学生信息管理系统或是图书管理系统试试喲！

如有错误或者不足之处可以在评论区留言！感谢你的观看！