Tracing Knowledge State with Individual Cognition and Acquisition Estimation 阅读笔记

Reference
Ting Long, Yunfei Liu, Jian Shen, Weinan Zhang, Yong Yu. 2021. Tracing
Knowledge State with Individual Cognition and Acquisition Estimation. In
Proceedings of the 44th International ACM SIGIR Conference on Research and
Development in Information Retrieval (SIGIR ’21), July 11–15, 2021, Virtual
Event, Canada. ACM, New York, NY, USA, 10 pages. https://doi.org/10.1145/
3404835.3462827
1
2
3
4
5
6
7

原文链接：https://dl.acm.org/doi/10.1145/3404835.3462827

在线学习网站面临的一个关键问题：动态评估学生的学习状态，找出学生难以回答的问题，并将其推入学生的待回答列表。Knowledge Tracing有利于在线教育中的相关任务，如安排个人学习路径，推荐学习材料。
深度学习拥有强大的学习能力，因此很多人致力于设计知识追踪的深度模型，比如基于拥有auto-regressive结构的深度学习模型RNN的KT模型。该模型中学生的知识状态(概念的掌握水平)由循环单元的隐藏状态表示，框架由read和write两个阶段组成，框架结构如下图所示：

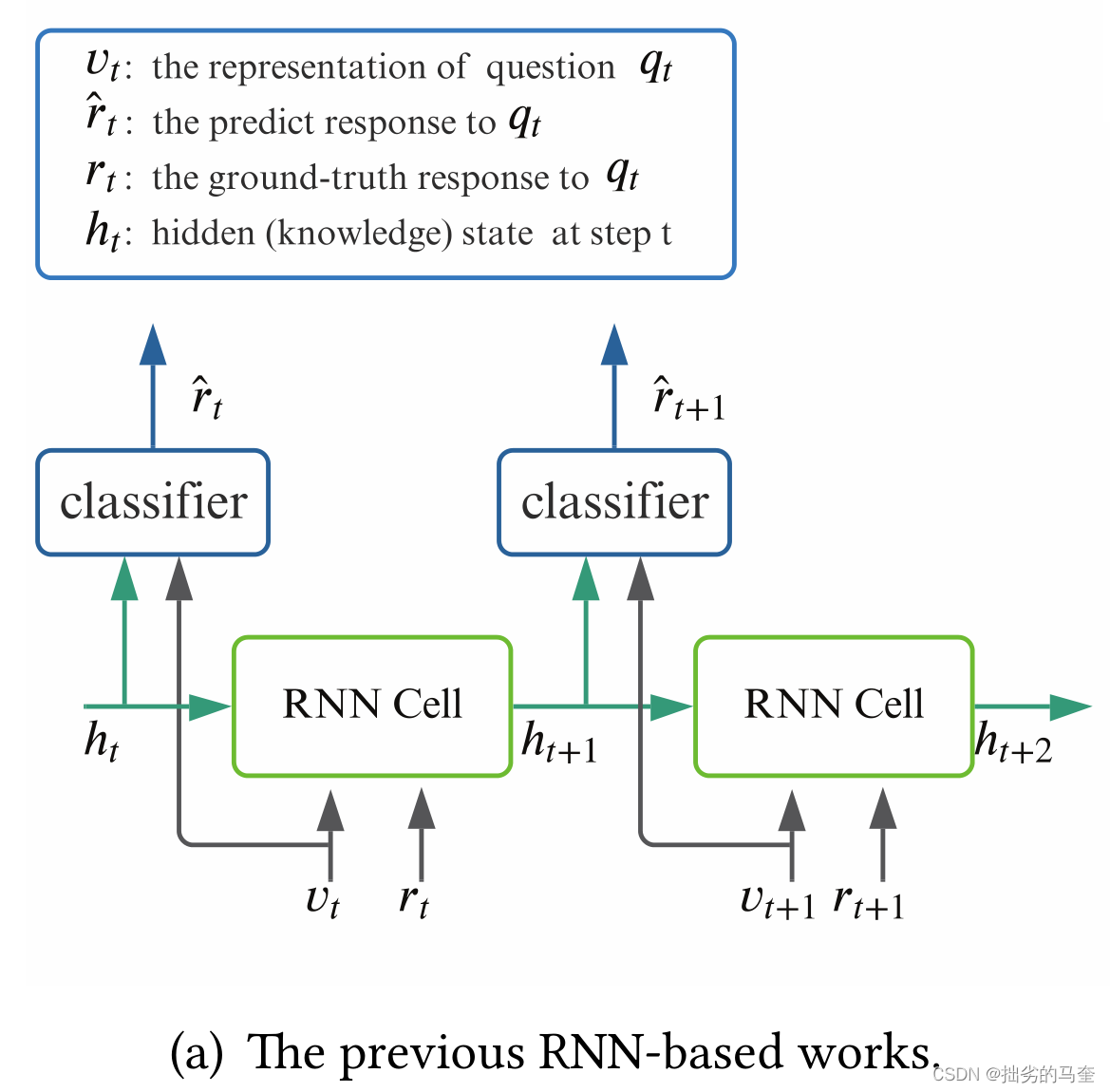
在read阶段，将recurrent cell的隐含状态和问题表征加载到多层感知器中，预测学生正确回答问题的概率。write阶段通过在收到一个问题的反馈后更新相应的recurrent cell来模拟学生知识状态的动态变化。

1. motivation

上述KT模型存在缺陷：
（1）认为学生认知水平一致（cognition level一致）
（2）认为学生在相同的学习条件下可以获得相同的知识增量（acquisition sensitivity一致）
缺乏对cognition level和acquisition sensitivity的显式建模限制了模型的表现。

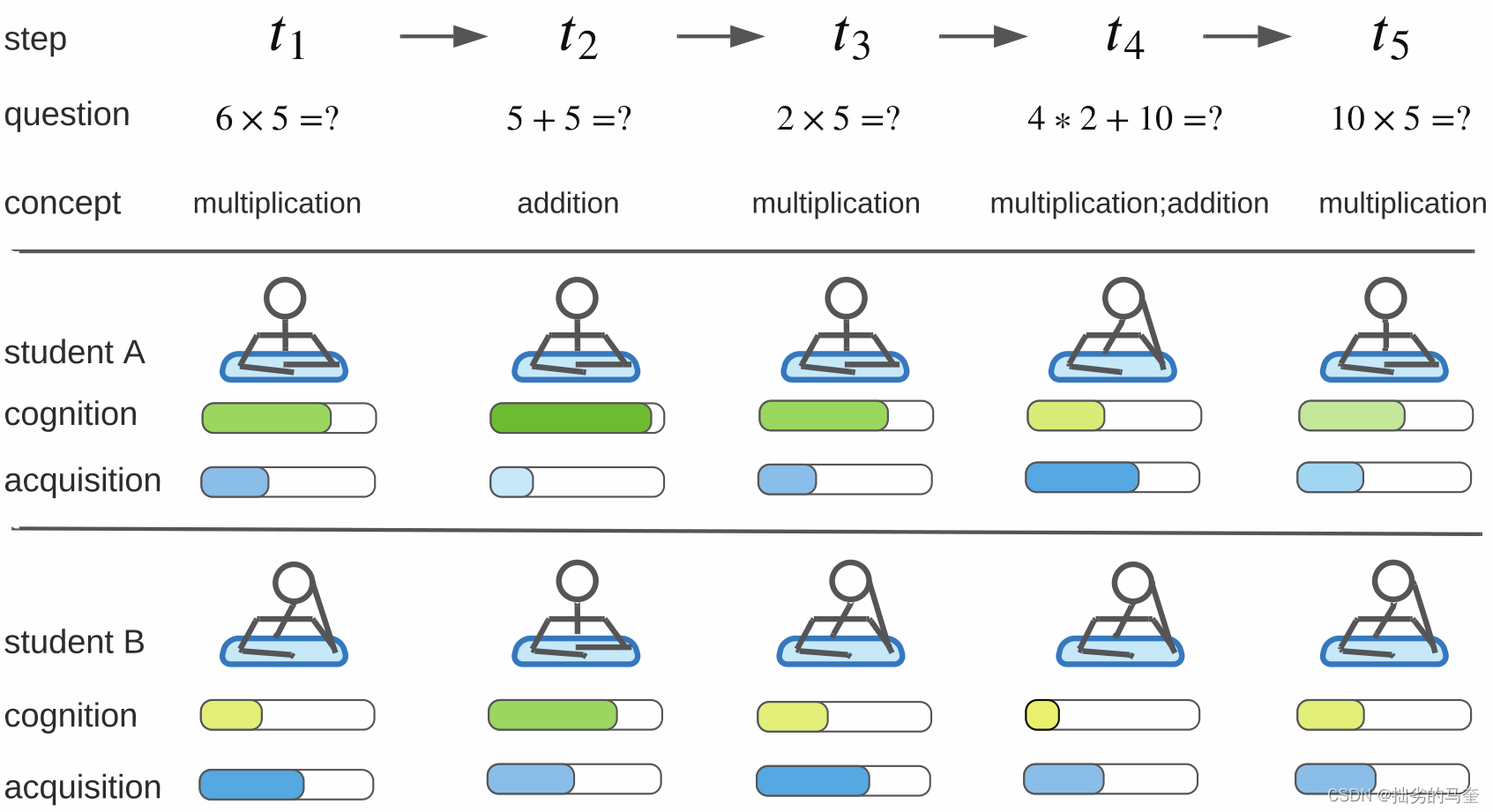
（注：一个question可能包含多个concepts）

为解决这两个缺陷，文章提出Individual Estimation Knowledge Tracing(IEKT) 模型

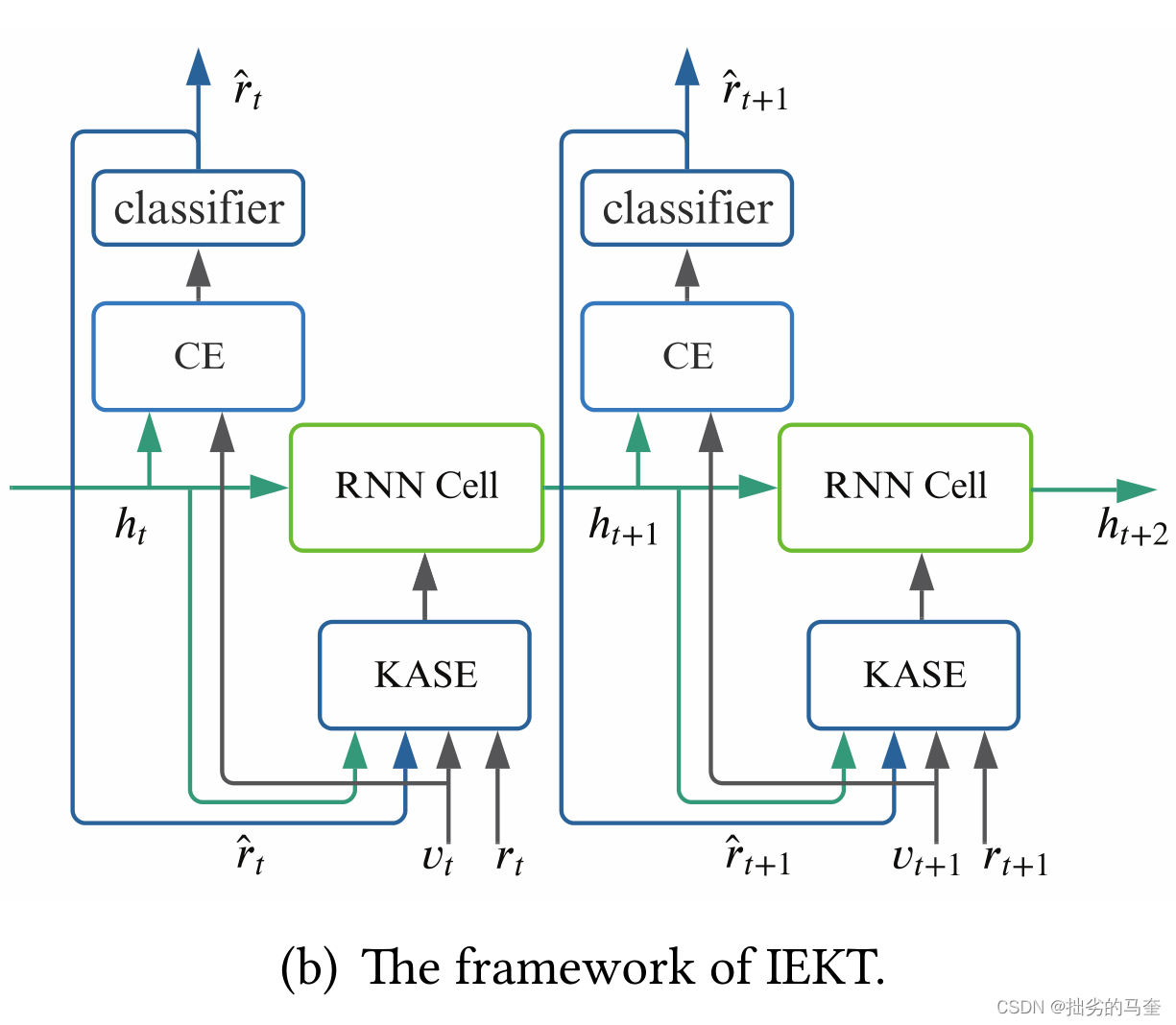
IEKT在
（1）read阶段加入cognition estimation（CE）模块，根据学生的知识状态、问题的表征来估计学生的cognition level。
（2）write阶段加入knowledge acquisition sensitivity estimation（KASE）模块，根据学生的知识状态，问题的表征，预测回答和真实回答，估计学生的acquisition sensitivity。
使用强化学习方法训练IEKT，实验结果表明IEKT达到了SOTA水平。

2. contributions

• 引入CE和KASE模块
• 在四个公开数据集上验证IEKT，其性能优于比较的基线
• 实验表明其他KT模型中引入CE和KASE模块也课提高性能

（KT模型相关工作见survey）

3. problem definition

KT问题涉及的符号含义如下表所示：

X t − 1 = { ( q 1 , r 1 ) , ( q 2 , r 2 ) , … , ( q t − 1 , r t − 1 ) } \mathcal{X}_{t-1}=\left\{\left(q_{1}, r_{1}\right),\left(q_{2}, r_{2}\right), \ldots,\left(q_{t-1}, r_{t-1}\right)\right\} Xt−1​={(q1​,r1​),(q2​,r2​),…,(qt−1​,rt−1​)}其中$q_t$是step t时的问题，$r_t$是学生回答的标签：
r t = { 1 ,  if the student’s answer is right;  0 ,  otherwise  r_{t}=\left\{

$$\begin{array}{l} 1, \text { if the student's answer is right; } \\ 0, \text { otherwise } \end{array}$$ \right. rt​={1, if the student’s answer is right; 0, otherwise ​
$e_i^q$是问题$q_i$的embedding，$e_j^c$是概念$c_j$的embedding。
KT任务目标是在历史记录基础上，预测step t时回答对新问题$q_t$的概率：$P\left(r_t=1\mid q_t,X_{t-1}\right)$。通过学习由参数集$\Theta$参数化的函数$f_{\Theta }$来预测概率：
$${\hat{r}}_t=f_{\Theta }(\cdot )$$
${\hat{r}}_t=P\left(r_t=1\mid q_t,X_{t-1}\right),(\cdot )$表示用于预测学生回答的特征。
知识状态${\mathbf{h}}_t$反映某学生掌握所有concepts的水平。
cognition level 是学生对于一个问题$q_t$的理解水平，用向量${\mathbf{m}}_t$表示。k种不同的cognition levels组成了cognition矩阵$\mathbf{M}\in {\mathbf{R}}^{k\times d_m}$ 。
knowledge acquisition sensitivity 反映学生回答问题$q_t$并收到反馈后的知识增量，用向量${\mathbf{s}}_{\mathbf{t}}$表示。b种不同的acquisition sensitivities组成acquisition矩阵$\mathbf{S}\in {\mathbf{R}}^{b\times d_S}$。

4. method

4.1 the read stage

(1) 一个问题可以表征为：${\mathbf{v}}_t={\mathbf{e}}_t^q\oplus {\overline{\mathbf{e}}}_t^c$，${\overline{\mathbf{e}}}_t^c$是问题$q_t$涉及concept embeddings的均值，$\oplus$是concatenate操作，则${\mathbf{v}}_t\in {\mathbf{R}}^{d_q+d_c}$。
(2) 将问题表征${\mathbf{v}}_t$与知识状态${\mathbf{h}}_t$进行concatenate操作：${\mathbf{h}}_v={\mathbf{h}}_t\oplus {\mathbf{v}}_t$，则${\mathbf{h}}_t\in {\mathbf{R}}^{d_h+d_q+d_c}$
(3) 通过映射函数$f_p$获得cognition vectors的索引概率分布，从中采样得到一个索引$i_{m,t}\sim f_p\left({\mathbf{h}}_v\right)$
(4) 根据索引在cognition矩阵中获得cognition向量${\mathbf{m}}_t=\mathbf{M}\left[i_{m,t}\right]$
(5) 学生正确回答问题$q_t$的概率可估计为：
y t = ReLU ⁡ ( W 1 ⋅ [ m t ⊕ h v ] + b 1 ) , r ^ t = δ ( W 2 ⋅ y t + b 2 ) ,

$$\begin{array}{l} \mathbf{y}_{t}=\operatorname{ReLU}\left(\mathbf{W}_{1} \cdot\left[\mathbf{m}_{t} \oplus \mathbf{h}_{v}\right]+\mathbf{b}_{1}\right), \\ \hat{r}_{t}=\delta\left(\mathbf{W}_{2} \cdot \mathbf{y}_{t}+\mathbf{b}_{2}\right), \end{array}$$ yt​=ReLU(W1​⋅[mt​⊕hv​]+b1​),r^t​=δ(W2​⋅yt​+b2​),​
${\mathbf{W}}_1,{\mathbf{W}}_2,{\mathbf{b}}_1,{\mathbf{b}}_2$是可训练参数
${\mathbf{W}}_1\in {\mathbf{R}}^{d_r\times d_r}，d_r=d_v+d_m,{\mathbf{W}}_2\in {\mathbf{R}}^{d_r\times 1},{\mathbf{b}}_1\in {\mathbf{R}}^{d_r},{\mathbf{b}}_2\in \mathbf{R}.$
$\delta$ 是sigmoid 函数:$\delta (\mathbf{x})=\frac{1}{1+e^{-\mathbf{x}}}$

4.2 the write stage

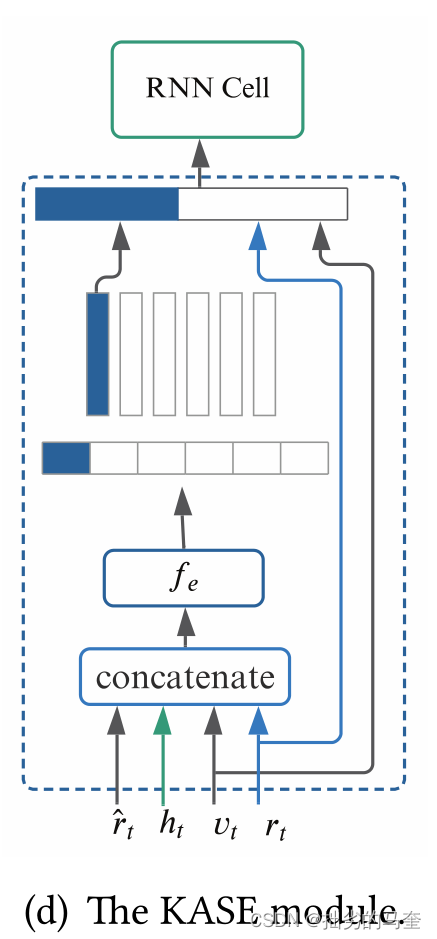
(1) 将${\mathbf{h}}_v$与预测结果进行concatenate操作：
v p = { h v ⊕ 0 , r ^ t ≥ 0.5 0 ⊕ h v , r ^ t < 0.5 \mathbf{v}_{p}=\left\{

$$\begin{array}{ll} \mathbf{h}_{v} \oplus \mathbf{0}, & \hat{r}_{t} \geq 0.5 \\ \mathbf{0} \oplus \mathbf{h}_{v}, & \hat{r}_{t}<0.5 \end{array}$$ \right. vp​={hv​⊕0,0⊕hv​,​r^t​≥0.5r^t​<0.5​
$0\in {\mathbf{R}}^{d_v}$
(2) 将${\mathbf{h}}_v$与ground-truth进行concatenate操作：
$${\mathbf{v}}_g=\{\begin{array}{l}{\mathbf{h}}_v\oplus 0,r_t=1\\ 0\oplus {\mathbf{h}}_v,r_t=0\end{array}$$
$0\in {\mathbf{R}}^{d_v}$
(3) 将以上两个concatenations进行concatenate操作：
$${\mathbf{v}}_m={\mathbf{v}}_p\oplus {\mathbf{v}}_g$$
作者希望借助（3）可以达到在交互过程中学生蒙对或漏题引起的噪声影响。
(4) 通过映射函数$f_e$从acquisition矩阵$\mathbf{S}$获得一个acquisition向量：
$$\begin{array}{rl}{\mathbf{i}}_{s,t}& \sim f_e\left({\mathbf{v}}_m\right),\\ {\mathbf{s}}_t& =\mathbf{S}\left[i_{s,t}\right].\end{array}$$
(5) 将问题表征${\mathbf{v}}_i$与acquisition向量${\mathbf{s}}_t$进行concatenate操作：
$${\mathbf{v}}_i=\{\begin{array}{l}{\mathbf{v}}_t\oplus {\mathbf{s}}_t,r_t=1,\\ {\mathbf{s}}_t\oplus {\mathbf{v}}_t,r_t=0\end{array}$$
(6) 将${\mathbf{v}}_i$和当前知识状态${\mathbf{h}}_t$喂入RNN cell来更新知识状态，文章采用GRU结构：
$$\begin{array}{rl}{\mathbf{u}}_r& =\delta \left({\mathbf{W}}_r\cdot \left({\mathbf{v}}_i\oplus {\mathbf{h}}_t\right)+{\mathbf{b}}_r\right)\\ {\mathbf{u}}_z& =\delta \left({\mathbf{W}}_z\cdot \left({\mathbf{v}}_i\oplus {\mathbf{h}}_t\right)+{\mathbf{b}}_z\right)\\ {\mathbf{u}}_h& =\tanh \left({\mathbf{W}}_h\cdot \left({\mathbf{v}}_i\oplus \left({\mathbf{u}}_r\ast {\mathbf{h}}_t\right)\right)+{\mathbf{b}}_h\right)\\ {\mathbf{h}}_{t+1}& =\left(1-{\mathbf{u}}_z\right)\ast {\mathbf{u}}_h+u_z\ast {\mathbf{h}}_t.\end{array}$$
${\mathbf{W}}_r,{\mathbf{b}}_r,{\mathbf{W}}_z,{\mathbf{b}}_z,{\mathbf{W}}_h,{\mathbf{b}}_h$ 是可训练参数
${\mathbf{W}}_r,{\mathbf{W}}_z,{\mathbf{W}}_h\in {\mathbf{R}}^{d_h\times \left(d_i+d_h\right)}$，${\mathbf{b}}_r,{\mathbf{b}}_z,{\mathbf{b}}_h\in {\mathbf{R}}^{d_h}$

4.3 model learning

4.1（3）和4.2（4）中直接采样获取向量，无法计算梯度，故采用强化学习算法中的Policy Gradient去优化cognition向量和acquisition向量的选取。

• 对于4.1（3）中采样获取cognition向量，将${\mathbf{h}}_v$作为强化学习的state。action set A m = { 0 , 1 , 2 , . . . , k } A_m=\{0,1,2,...,k\} Am​={0,1,2,...,k}，其中元素代表着cognition vector的索引（$\mathbf{M}\in {\mathbf{R}}^{k\times d_c}$），4.1（3）中的映射函数$f_p$可以反映”随机stochastic“。reward定义为：
  u ^ t = { 1 T ,  if the prediction is correct,  0 ,  otherwise  \hat{u}_{t}=\left\{

  $$\begin{array}{l} \frac{1}{T}, \text { if the prediction is correct, } \\ 0, \text { otherwise } \end{array}$$ \right. u^t​={T1​, if the prediction is correct, 0, otherwise ​
  T表示问答序列的长度。
  cognition向量选择的损失函数定义为：
  ${\mathcal{L}}_m=-{\sum }_t^T\log f_p\left(i_{m,t}\mid {\mathbf{h}}_v\right)u_t$
  $u_t$表示在step t时的累积reward，可由${\hat{u}}_t$计算得到：
  $$u_t={\hat{u}}_t+\gamma u_{t+1}$$
  $\gamma$是discount factor。

• 对于4.2（4）中采样获取acquisition向量，action set A m = { 0 , 1 , 2 , . . . , b } A_m=\{0,1,2,...,b\} Am​={0,1,2,...,b}，其中元素代表acquisition vector的索引（$\mathbf{S}\in {\mathbf{R}}^{b\times d_s}$），同理，acquisition向量选择的损失函数可定义为：
  $${\mathcal{L}}_s=-\sum _t^T\log f_e\left(i_{s,t}\mid {\mathbf{v}}_m\right)u_t$$

则我们的目标是最小化损失函数：${\mathcal{L}}_{ms}={\mathcal{L}}_m+{\mathcal{L}}_s$
KT任务的目标函数是预测概率${\hat{r}}_t$和真实标签$r_t$的负对数似然，即：
$${\mathcal{L}}_c=-\sum _{i=1}^T\left(r_i\log {\hat{r}}_i+\left(1-r_i\right)\log \left(1-{\hat{r}}_i\right)\right)$$
最终的损失函数为：
$$\mathcal{L}={\mathcal{L}}_c+\lambda {\mathcal{L}}_{ms}$$
训练IEKT的算法代码如下图所示：

5. experiment results

在四个数据集和十一个baselines上进行实验，IEKT相比baselines在多个指标上均有提升。
IEKT方法基本框架与DHKT相似，但明显好于DHKT，这意味着将CE和KASE模块引入知识跟踪有利于提高性能。
基于深度学习的方法在大多数情况下都优于传统方法。然而，在某些情况下，传统方法具有类似甚至更好的性能。

消融实验

作者为研究CE模块和KASE模块的贡献，进行了消融实验。
结果表明，无论移除模型的哪个模块，IEKT的性能都会下降，并且发现去除KASE对性能的影响比去除CE更显著。作者分析认为原因在于KASE影响未来的所有预测，而CE只影响当前的响应预测。
将CE和KASE应用于其他的框架，实验结果表明大多数情况下引入CE和KASE可以提高性能。

作者还设计了实验证明了去除强化学习的最优化方法也会影响IEKT的性能。

sensitivity analysis

采用不同的超参数测试IEKT的性能，发现ACC和AUC没有明显波动，说明IEKT具有很好的稳定性，模型的最优超参数可以很容易找到

vector distributions

cognition向量之间的相似性和acquisition向量之间的相似性如图所示：

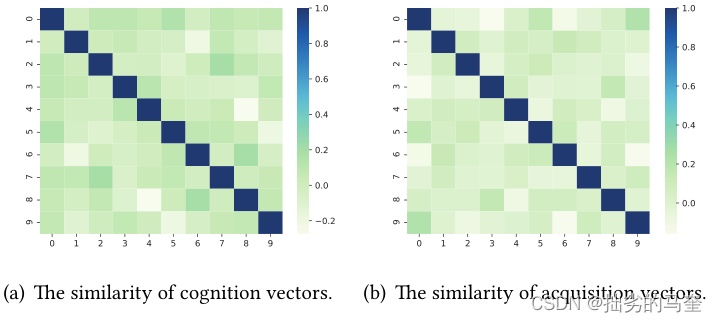
不同向量之间区分度大。

由于学生的认知水平和知识获取敏感度代表了学生的学习能力，我们将所选向量指标的分布与答题准确率进行对比，如图7所示。与离线教育场景中的许多答题和考试结果一样，学生在该数据集中的准确性也接近z分数分布，如图7©所示。

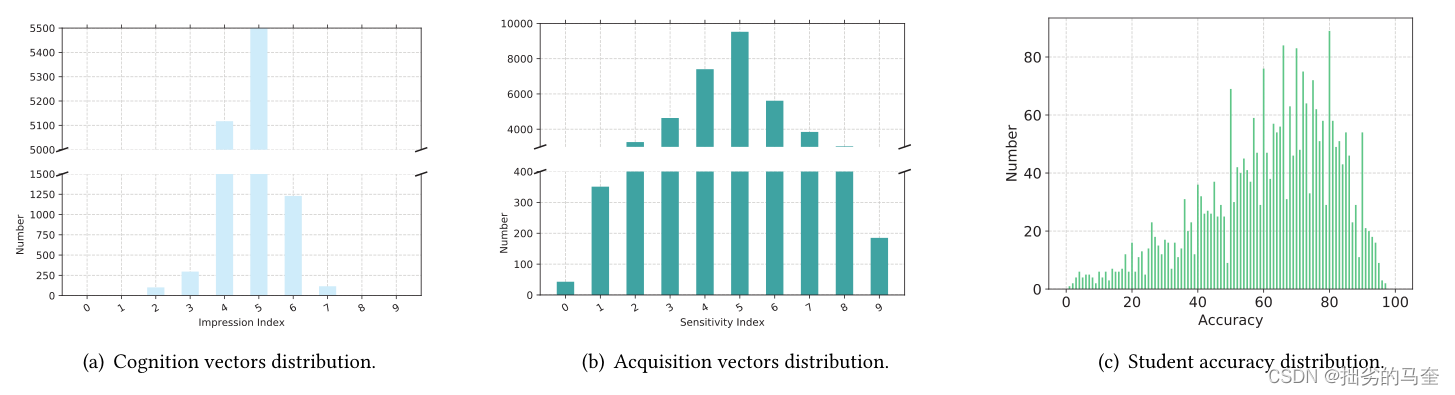
可以观察到cognition向量和acquisition向量的选择，如图7(a)和(b)所示。有些cognition向量和acquisition向量被多次选取，有些则被有限次选取，表明模型学习到一些cognition向量和acquisition向量是许多学生共有的，但有些只适用于少数学生。这意味着大多数学生对同一个问题有相似的理解，少数学生对这个问题有不同的理解。

此外，大多数学生的knowledge acquisition sensitivity一般。但也有少部分学生对问题有较强的敏感度。他们可以在与相关问题的几次互动中掌握一个知识概念，但有些学生需要在学习上付出更多的努力。这与图7©中回答问题的准确性所反映的能力是一致的，有很多学生的正确率在50% - 85%之间。但是，正确率低于50%或高于85%的学生数量很少。。

6. 展望

作者发现模型选择的acquisition向量集中在acquisition矩阵的一小部分上，这意味着模型的学习结果与真实学生能力的分布之间存在差距，期待未来弥补这一不足。

（待精读解决：有没有考虑遗忘？能不能引入注意力机制&效果会更好吗？可不可以将采样分布与真实分布之间的差距作为损失函数的一项来改进？）
1