互相关延时估计 Matlab仿真_广义互相关时延估计算法代码

互相关延时估计

互相关延时估计是一种信号处理技术，用于计算两个信号之间的时间延迟。在本篇博客中，我们将使用MATLAB来实现互相关延时估计，并提供多个例子和代码，以帮助更好地理解该技术。

什么是互相关延时估计？

互相关延时估计是通过比较两个信号的相似性来计算它们之间的时间延迟。在信号处理中，时间延迟是指一个信号相对于另一个信号的延迟时间。互相关延时估计在许多领域中都有广泛应用，包括语音识别、音频处理、图像处理等。

原理

当计算互相关函数时，可以将其中一个信号向右移动$k$个样本，然后将该信号与另一个信号的每个样本相乘并求和。最后，将计算的结果作为互相关函数的值。

举一个简单的例子来说明如何计算互相关函数。假设我们有两个信号 x = { 1 , 2 , 3 } x = \{1, 2, 3\} x={1,2,3} 和 y = { 2 , 1 , 1 } y = \{2, 1, 1\} y={2,1,1}。我们想要计算这两个信号之间的互相关函数。根据互相关函数的定义，我们可以得到：

$$R_{xy}(k)=\sum _{n=-\infty }^{\infty }x(n)y(n-k)$$

我们可以通过手动计算互相关函数来理解它的计算过程。具体来说，我们可以将信号 $x$ 向右移动 $k$ 个样本，然后将其与信号 $y$ 的每个样本相乘并求和。在这个例子中，我们手动计算得到这两个信号之间的互相关函数为 R x y = { 7 , 3 , 1 , 0 , 0 } R_{xy} = \{7, 3, 1, 0, 0\} Rxy​={7,3,1,0,0}。其中，$R_{xy}(0)$ 是互相关函数的最大值，对应于两个信号之间的最佳延迟。

在信号处理中，我们经常需要将两个信号进行比较。但是，由于信号可能会出现时间偏移，因此需要将信号进行时间同步，以便进行比较。这个时间偏移就是我们这里所说的延迟。延迟是指一个信号相对于另一个信号的时间偏移量。

在Matlab中，可以使用内置的xcorr函数来计算互相关函数。对于这个例子，我们可以使用以下代码计算互相关函数：

x = [1, 2, 3];
y = [2, 1, 1];
[corr, lag] = xcorr(x, y);
1
2
3

最后，corr向量中的最大值对应于延迟0，即两个信号之间没有延迟。而在这个例子中，我们手动计算得到的最大值是在延迟0的位置，与Matlab计算的结果相符。

因此，使用互相关函数进行延时估计可以帮助我们在信号处理中对信号进行时间同步，以便进一步处理。

代码实现

以下是一个简单的Matlab代码，用于计算两个信号之间的延迟：

% 生成两个信号
fs = 1000;  % 采样频率
t = 0:1/fs:1;  % 时间向量
x = sin(2*pi*50*t);  % 50 Hz正弦波
y = sin(2*pi*50*t + pi/2);  % 相位差为90度的50 Hz正弦波

% 计算互相关函数
[corr, lag] = xcorr(x, y);

% 找到延迟
[~,I] = max(abs(corr));
delay = lag(I);
delay_time = delay/fs; % 延迟时间

% 显示结果
fprintf('Delay between x and y is %f seconds.', delay_time);

% 绘制互相关函数图像
figure;
subplot(2,1,1);
plot(t, x, 'b', t, y, 'r');
xlabel('Time (s)');
ylabel('Amplitude');
title('Original Signals');
legend('Signal x', 'Signal y');

subplot(2,1,2);
plot(lag, corr);
xlabel('Lag');
ylabel('Correlation');
title('Cross-Correlation of x and y');


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

运行结果：
      Delay between x and y is 0.005000 seconds.
1
2

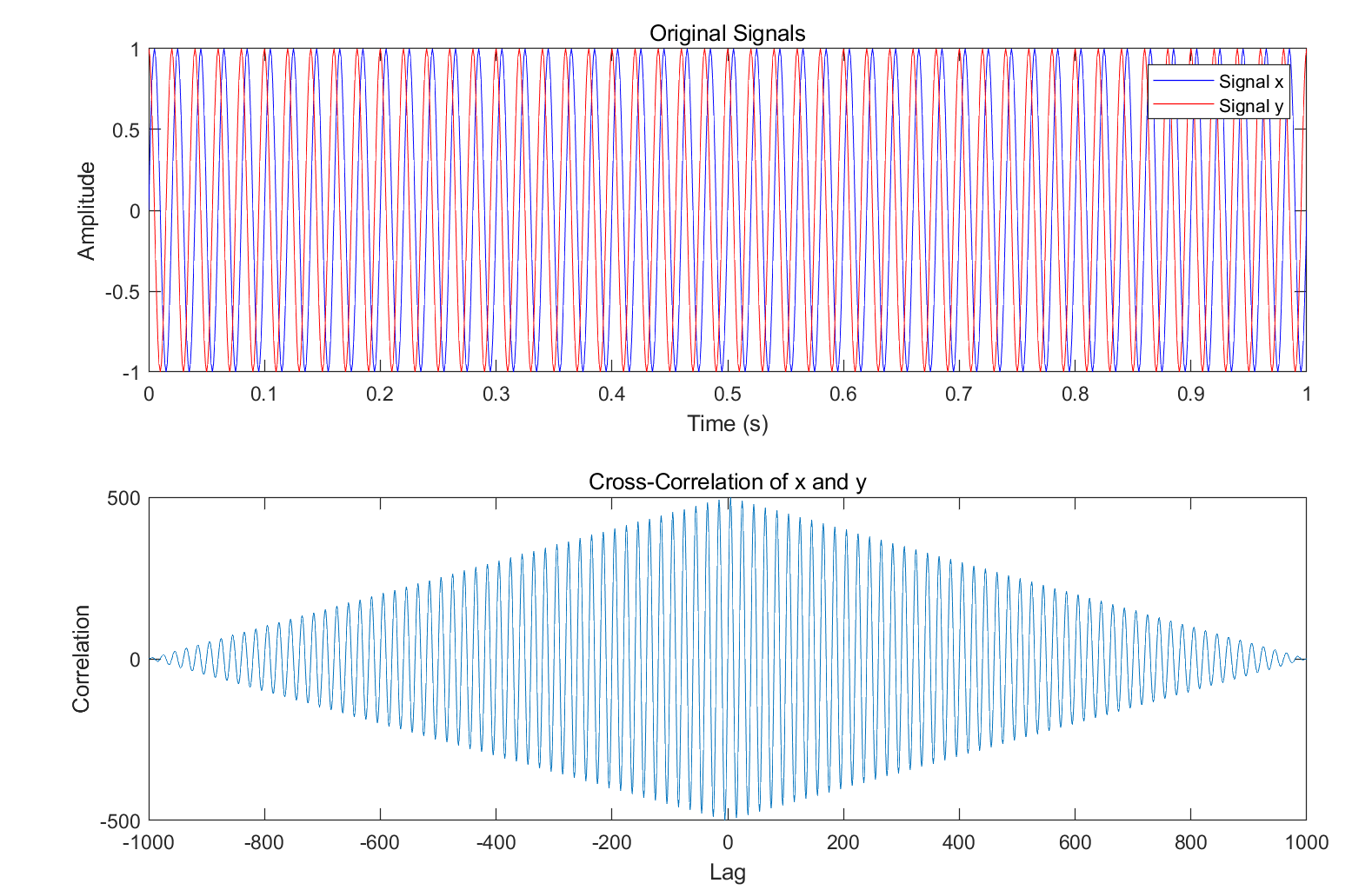
在上面的代码中，我们生成了两个相位差为90度的50Hz正弦波。然后我们使用xcorr函数计算它们之间的互相关函数。xcorr函数返回两个参数：corr和lag。corr是互相关函数的值，lag是所有延迟值的向量。我们使用max函数找到互相关函数的峰值，并使用lag找到对应的延迟。为了得到实际延迟时间，我们将延迟样本数除以采样频率。

互相关函数的计算原理是：将一个信号延迟$k$个样本，然后将其与另一个信号的每个样本相乘并求和。这个过程在式子$R_{xy}(k)={\sum }_{n=-\infty }^{\infty }x(n)y(n-k)$中表示。互相关函数的最大值对应于两个信号之间的最佳延迟。因此，我们可以使用互相关函数来估计两个信号之间的时间延迟。

除了上面的代码，我们还可以使用以下代码生成两个矩形波，并计算它们之间的延迟：

% 生成两个信号
fs = 1000;  % 采样频率
t = 0:1/fs:1;  % 时间向量
x = square(2*pi*50*t);  % 50 Hz矩形波
y = square(2*pi*50*t + pi/2);  % 相位差为90度的50 Hz矩形波

% 计算互相关函数
[corr, lag] = xcorr(x, y);

% 找到延迟
[~,I] = max(abs(corr));
delay = lag(I);
delay_time = delay/fs; % 延迟时间

% 显示结果
fprintf('Delay between x and y is %f seconds.', delay_time);

% 绘制互相关函数图像
figure;
plot(lag, corr);
xlabel('Lag');
ylabel('Correlation');
title('Cross-Correlation of x and y');
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

运行结果：
      Delay between x and y is 0.005000 seconds.
1
2

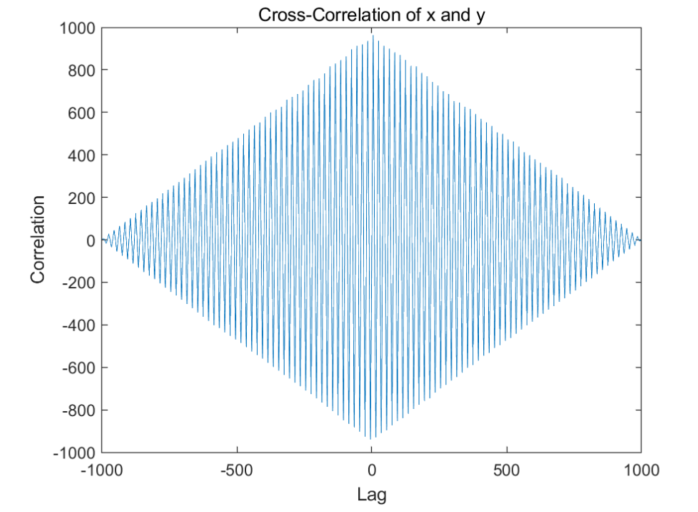
在上面的代码中，我们生成了两个相位差为90度的50Hz矩形波。然后我们使用xcorr函数计算它们之间的互相关函数。最后，我们找到互相关函数的峰值，并计算其对应的延迟。将延迟样本数除以采样频率，可以得到延迟时间。

此外，我们还可以使用以下代码生成两个噪声信号，并计算它们之间的延迟：

% 生成两个信号
fs = 1000;  % 采样频率
t = 0:1/fs:1;  % 时间向量
x = randn(size(t));  % 高斯白噪声
y = circshift(x, 100);  % 将x向右移动100个样本

% 计算互相关函数
[corr, lag] = xcorr(x, y);

% 找到延迟
[~,I] = max(abs(corr));
delay = lag(I);
delay_time = delay/fs; % 延迟时间

% 显示结果
fprintf('Delay between x and y is %f seconds.', delay_time);

% 绘制互相关函数图像
figure;
plot(lag, corr);
xlabel('Lag');
ylabel('Correlation');
title('Cross-Correlation of x and y');
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

输出结果
	Delay between x and y is -0.100000 seconds.
1
2

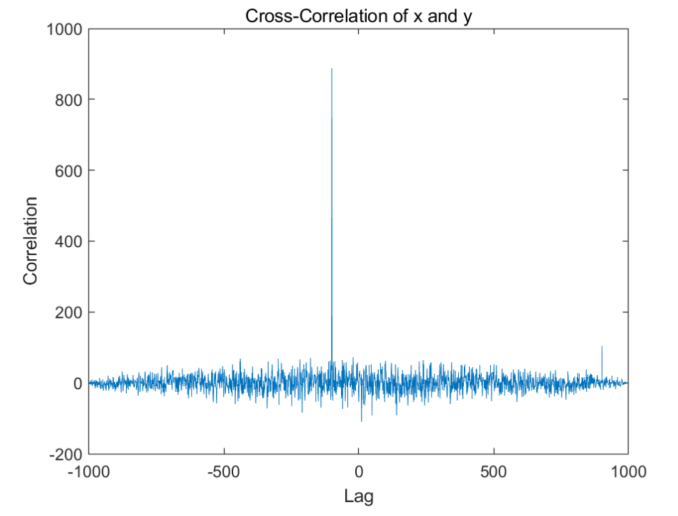
在上面的代码中，我们生成了两个高斯白噪声信号。然后我们将其中一个信号向右移动了100个样本，并使用xcorr函数计算了它们之间的互相关函数。最后，我们找到互相关函数的峰值，并计算其对应的延迟。将延迟样本数除以采样频率，可以得到延迟时间。

总结

本教程介绍了如何使用互相关函数进行延时估计。我们使用Matlab进行了代码实现和仿真。通过本教程，我们希望读者了解互相关函数的原理和应用，并能够使用Matlab实现延时估计。