算法——递归与搜索算法_递归搜索

1. 递归

①什么是递归？

官方一点来说

递归指的是一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法。

通俗一点来说，递归就是一个函数自己调用自己的过程

②什么情况下会用到递归？

我们在遇见一个问题的时候，我怎么知道这里可能会用到递归呢？这就需要我们了解递归的本质，即：在解决一个主问题时如果会衍生出一个相同的子问题，那么这里大概率就可以使用递归来解决。在这里举几个例子

1. 归并排序算法

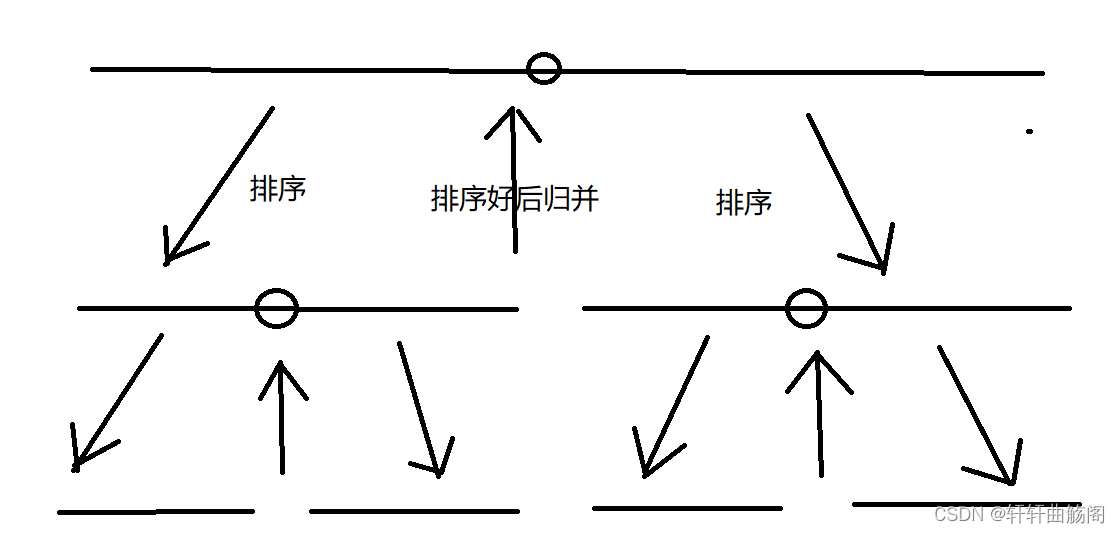
归并排序大致流程如图所示，我们想要对一个数组进行排序，就将它分为两半，对左边的数据排序好后，再对右边数据排序，左右数据排好后再将他们进行归并，为了解决排序的问题，我们将这个数组分为两半之后，我们又需要再分别对左右半边再次进行上述的操作

2. 快速排序算法

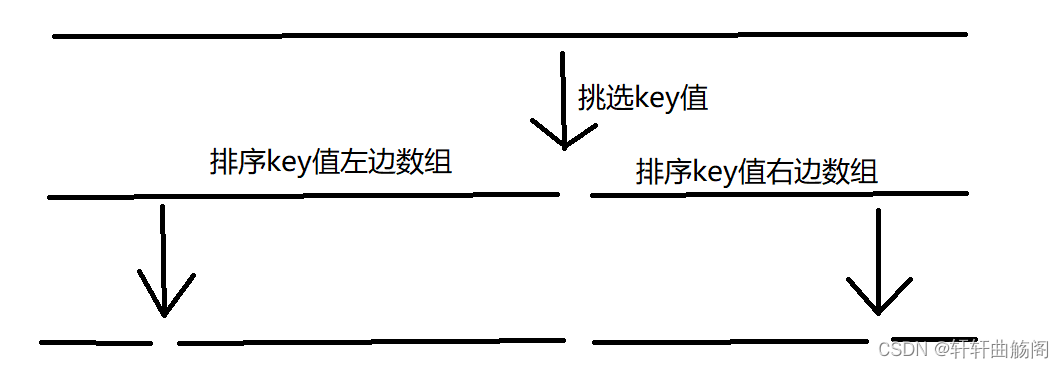
快速排序大致流程如图所示，我们想要对一个数组进行排序，就先挑选一个基准值key，将其移动到正确位置之后，对key左边的数组进行排序，再对key右边的数组排序，为了解决排序问题，我们将两边的数组排序之后，我们需要再次分别对左右部分挑选基准值并排序，即重复之前的过程

3. 二叉树的遍历

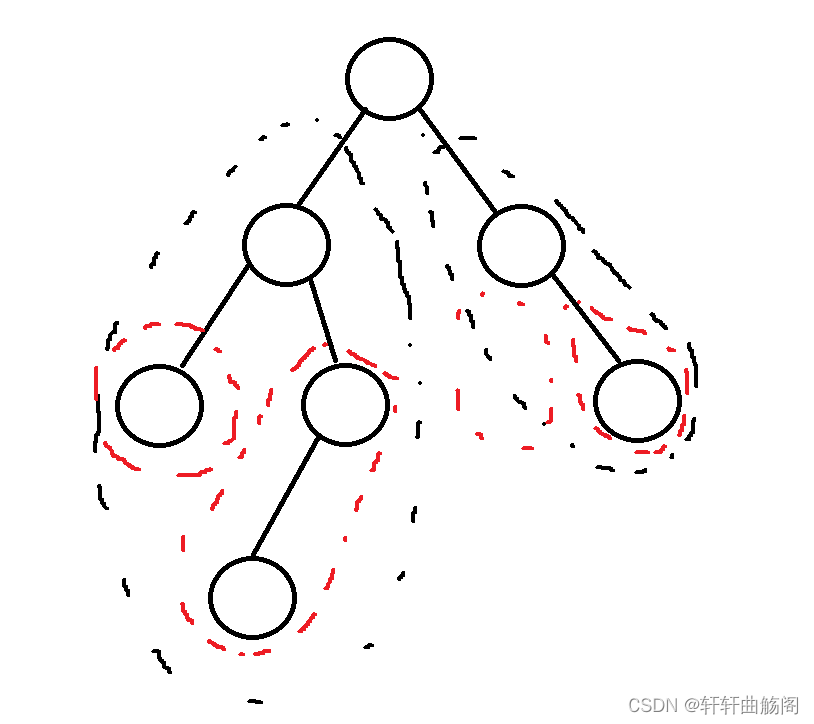
以上面这棵树为例，我们要对其进行后序遍历时，先要遍历左子树（左边黑色部分），然后遍历右子树（右边黑色部分），再访问自己，那么对于根节点的左子树来说，我们先遍历其左子树（左边红色部分），然后遍历其右子树（右边红色部分），本质上也是一种重复的过程

③如何理解递归？

在举例了上面几个例子之后，我们对递归应该有什么样的认识呢？我认为应该至少要有三点

1. 不要过于陷入递归展开图

2. 我们要将进行递归的函数视作一个黑盒

3. 在书写递归函数的过程中，我们要认为黑盒一定可以做到我们想做的事

在这里我们书写几个伪代码来实现上述部分例子

1. 归并

void merge(int nums[], int left, int right)
{
    // 出口
    if (left >= right) return;
    
    // 相信我们能够排序成功
    int mid = (left + right) / 2;
    merge(nums, left, mid);
    merge(nums, mid+1, right);
    // 排序好之后归并
    //...
}

2. 遍历

void dfs(Node* root)
{
    // 出口
    if (root == NULL) return;
    
    // 相信我们能够遍历成功
    dfs(root->left);
    dfs(root->right);
    // 遍历细节
    printf("%d ", root->val);
}

④如何写好一个递归？

在看了上面两个伪代码之后，我们可以知道要想写好一个递归，关键在于两点：

1. 要找到一个相同的子问题，即要设计好一个函数头

2. 具体解决好一个子问题即可，即书写递归函数主体

此外，为了避免函数进入死循环，需要给函数设计一个出口

2. 搜索

①深度优先遍历与深度优先搜索

在这里我们用一棵树来举例

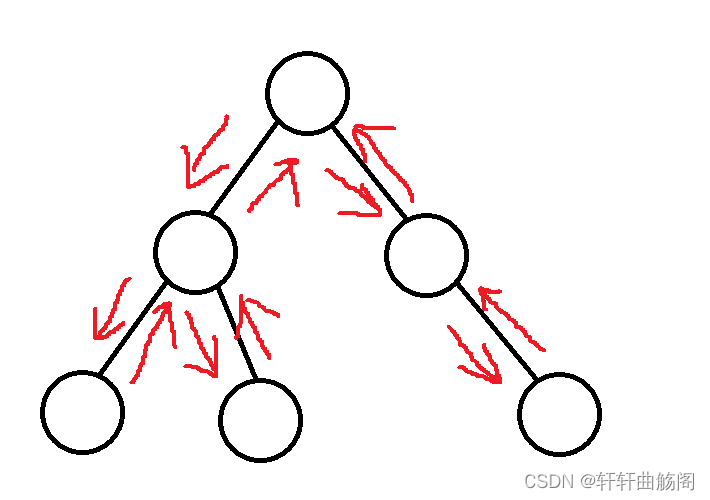
dfs即Depth-First Search，深度优先搜索，字面意思就是不断往深处搜索，搜索到头时返回上一个分支，然后继续往深处搜索，深度优先遍历与深度优先搜索，遍历是形式，搜索是目的

②广度优先遍历与广度优先搜索

bfs即Breadth-First Search，广度优先搜索，字面意思就是每次都遍历一层，然后不断地向外搜索

③拓展搜索问题

在这里我们以全排列问题为例，即

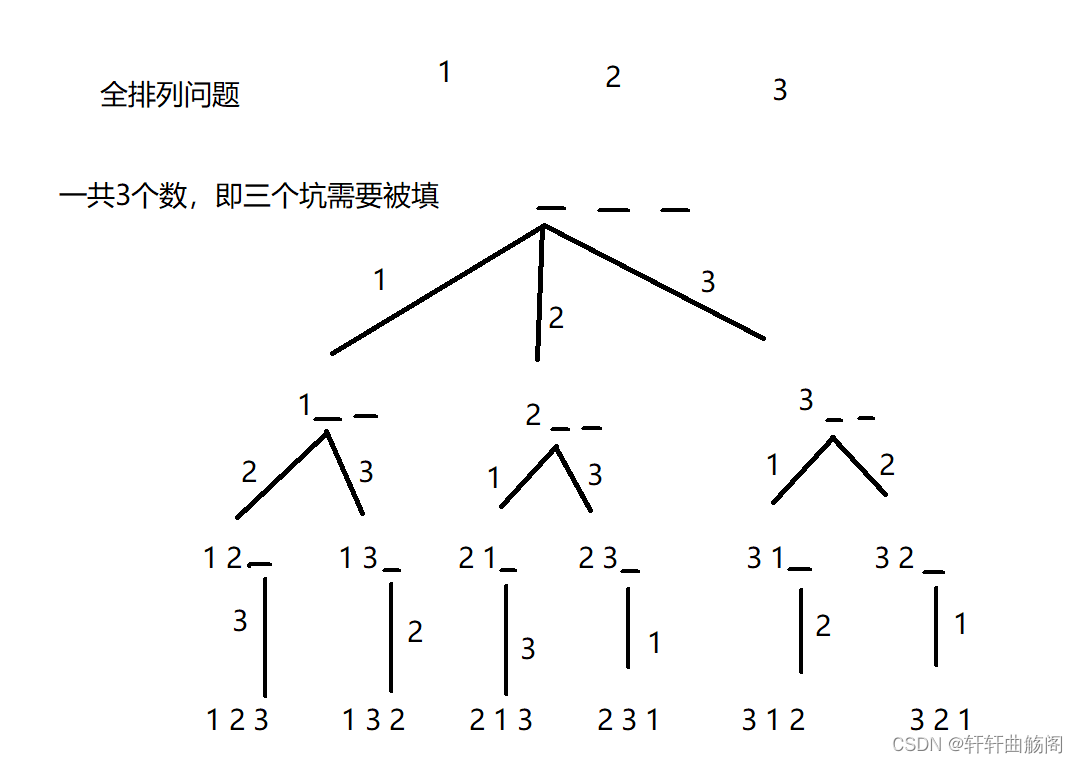
对于1,2,3三个数字来说，要找到它们的全排列，可以采取如上图所示的方式来做到，这之后我们只需要使用dfs或bfs就可以得到最后的全部结果，上面这种方式类似于树，我们也将其称为决策树

3. 回溯与剪枝

对于回溯我们可以将其视为与dfs相似，举个例子

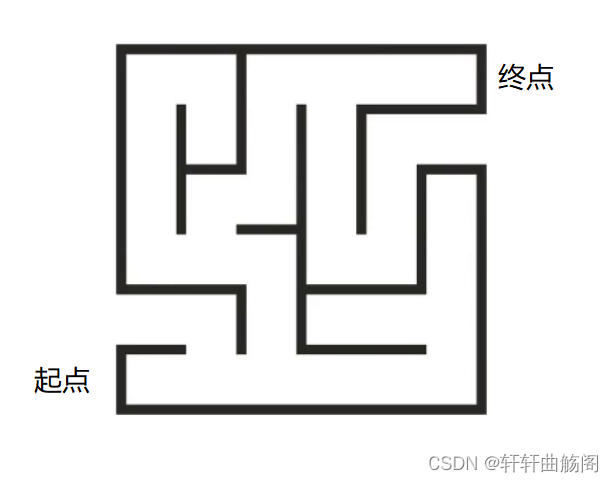
对于上面这个迷宫，我们从起点出发到第一个分叉点时，即

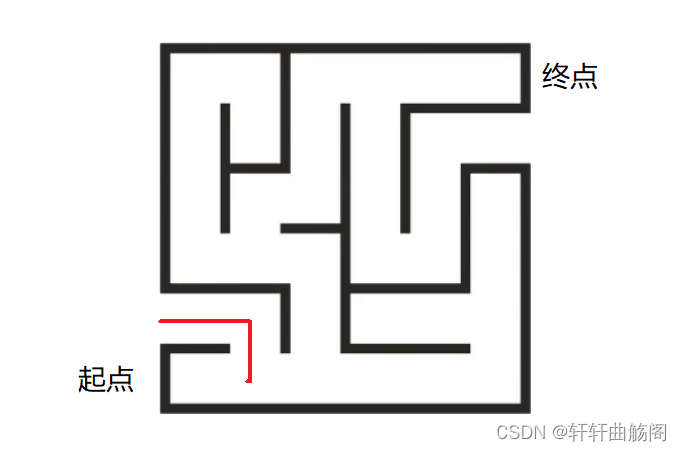
我们向左试探，发现这条路不能到达终点，因此需要我们进行回溯，即回到上一个分叉点

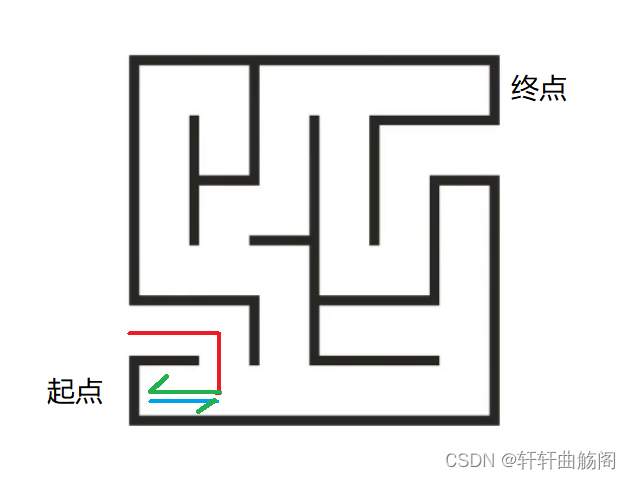
而在下面这种情况时，由于回到上一个分叉节点时，其有两种前进方式，而我们已经排除了其中的一种方式，此时我们需要对已经探索过的路径进行剪枝，即表示该路径无法到达终点

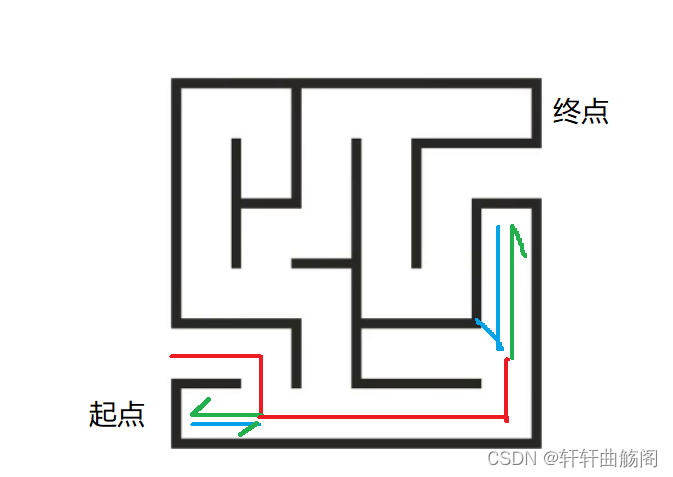
将其称为剪枝也是因为在树中访问过一个子树后，其就不用再次访问，即将树的枝条剪掉，是很形象的一个说法

4. 递归与循环（迭代）

在了解递归后，我们可以知道，递归解决的其实就是重复的问题，而循环也可以解决重复的问题，因此它们之间是可以互相转换的，那么在遇到一个既可以使用循环又可以使用递归的问题时，我们应该如何选择呢？

首先我们要知道，递归在展开后，我们可以发现它的路径和对一颗树进行dfs的路径是一样的，举个例子

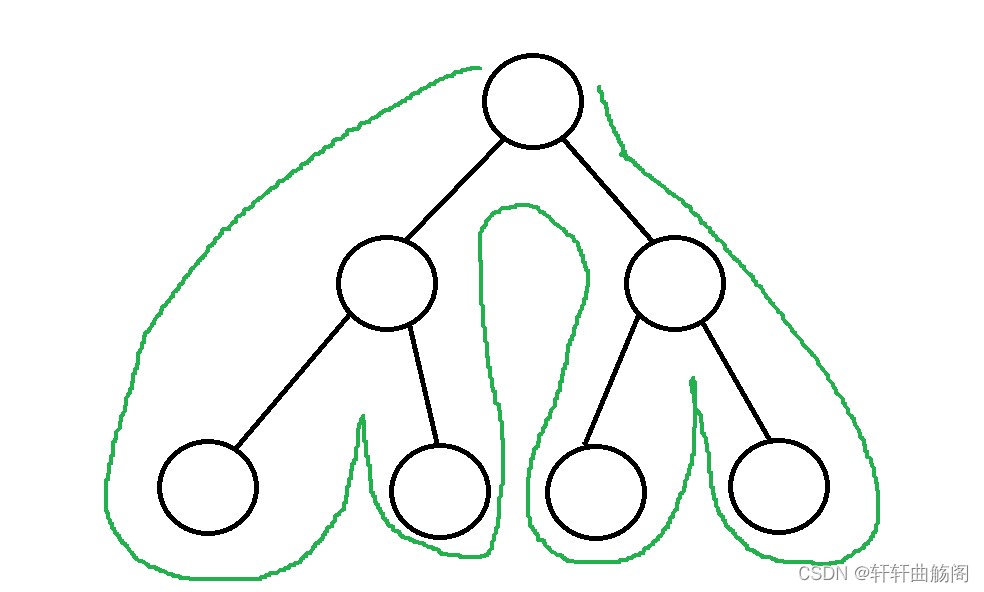
对于上面这棵树， 我们在递归解决它时，在深度递归完一条支路后需要返回到到上一个节点，即保存之前的信息，因此这里如果使用循环的话就需要使用栈来保存信息，因此此处使用递归更好，而在不需要保存信息的情况下，如遍历数组时，使用循环更佳

5. 例题

①递归专题

1. 汉诺塔问题

题目链接：面试题 08.06. 汉诺塔问题 - 力扣（LeetCode）

解析：题目说起来可能比较抽象，这里我们画图表示

大致要求是要让小的始终在上面，让后将A的所有圆盘移动到C上，我们在看到这个问题时，不能先入为主的想着用递归去解决它，而是在解决的过程中发现它具有一些递归的特性，然后才会想到使用递归解决它，那么我们如何解决它呢？这里我们可以使用先一般后特殊的方法

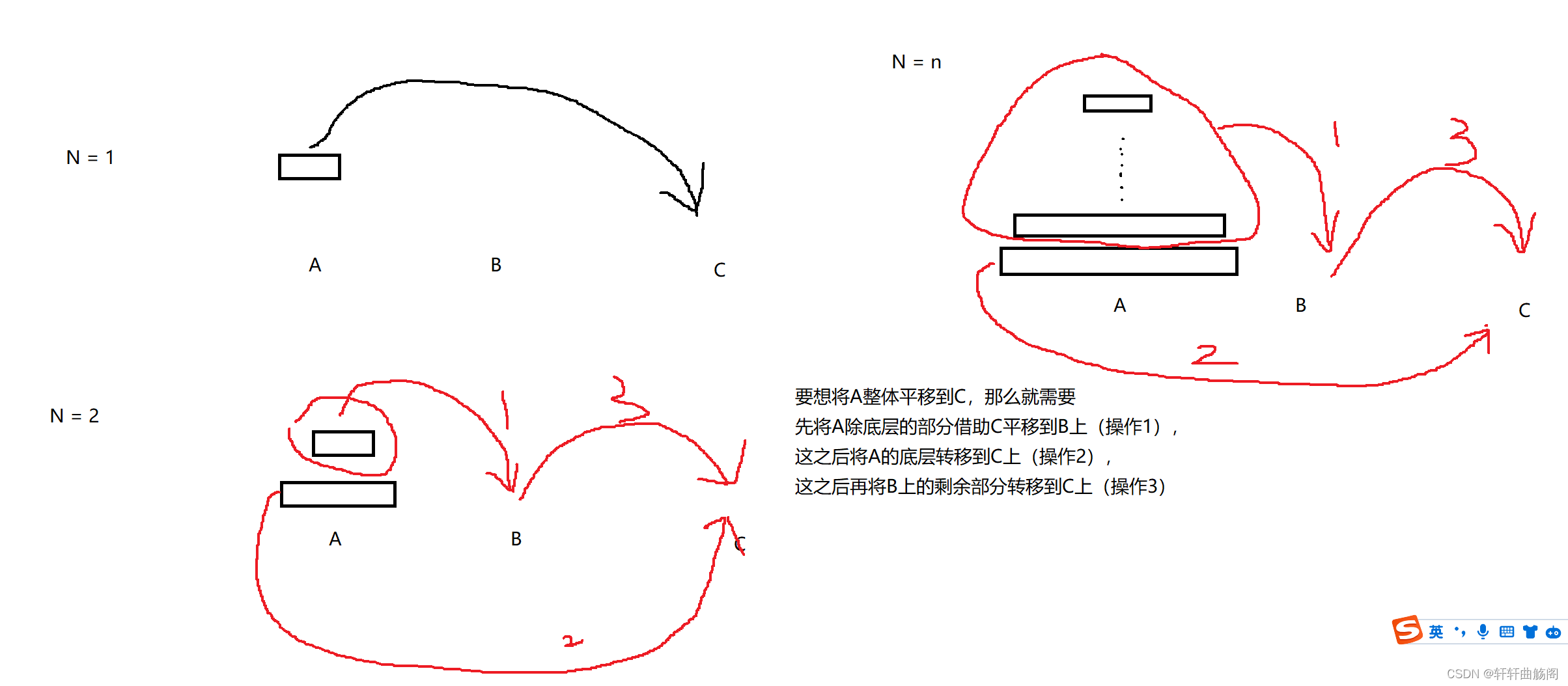
即在解决问题的过程中，我们可以发现在解决主问题时，衍生出来一个和他类似的子问题，而在解决子问题时，又出现一个和子问题相似的子问题，因此我们可以将其分解成若干个相同的子问题，即使用递归解决

其解决代码如下

class Solution 
{
public:
    void Hanota(vector<int>& A, vector<int>& B, vector<int>& C, int n)
    {
        // 出口
        if (n == 1) 
        {
            C.push_back(A.back());
            A.pop_back();
            return;
        }
 
        // 操作1：借助C杆，将A上的n-1个圆盘移动到B上
        Hanota(A, C, B, n-1);
        // 操作2：将A杆的底层转移到C杆上
        C.push_back(A.back());
        A.pop_back();
        // 操作3：将B上的剩余部分借助A，转移到C杆上
        Hanota(B, A, C, n-1); 
    }
 
    void hanota(vector<int>& A, vector<int>& B, vector<int>& C) 
    {
        int n = A.size();
        Hanota(A, B, C, n);
    }
};

注：在操作2中，不能直接向C直接插入A[0]，通过逐步拆分我们可以发现，虽然逻辑上来说，我们是将A除底层的整个部分直接平移的，但在实际上，我们是从最上面开始一个一个平移的，因此这里使用的是back元素。

2. 合并两个有序链表

题目链接：21. 合并两个有序链表 - 力扣（LeetCode）

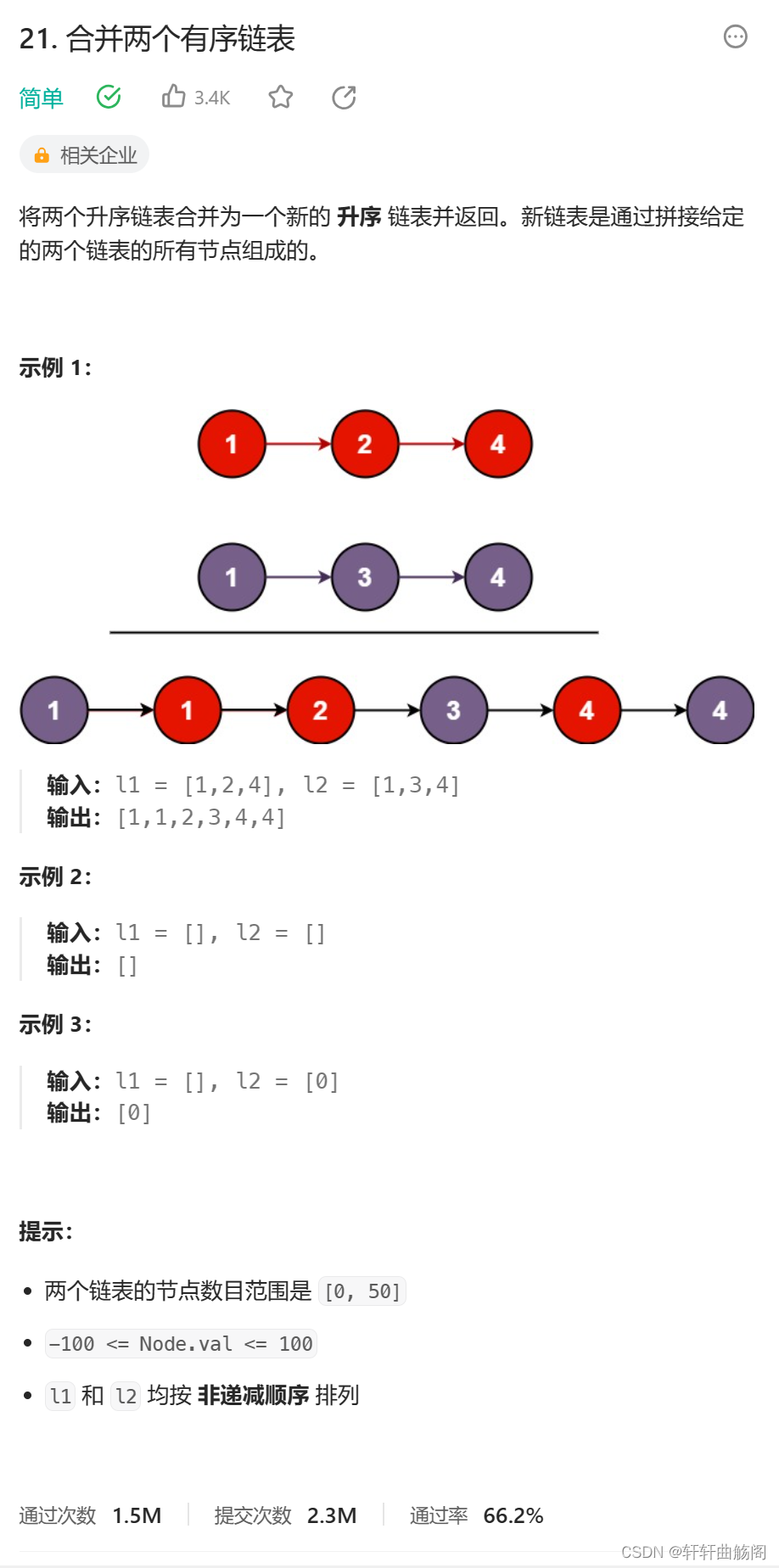
解析：

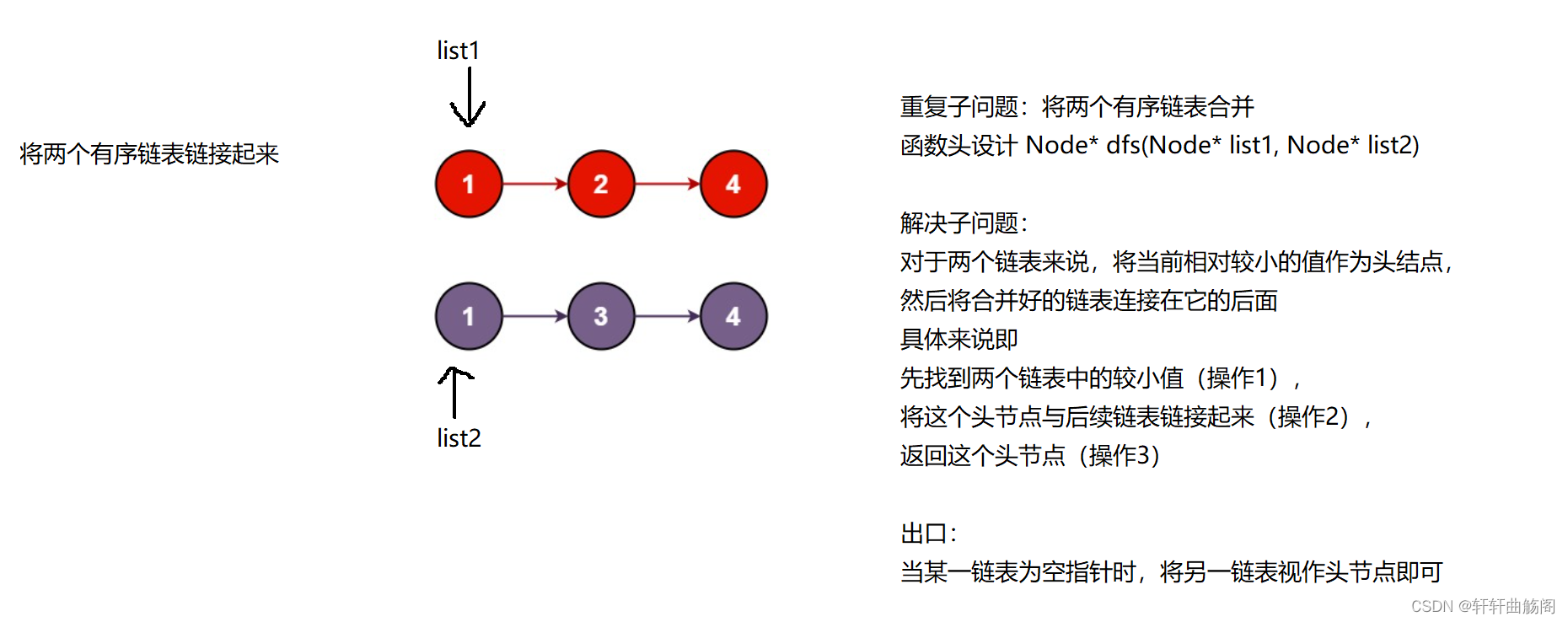
参考代码：

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) 
    {
         return dfs(list1, list2);   
    }
 
    ListNode* dfs(ListNode* list1, ListNode* list2) 
    {
        // 出口
        if (list1 == nullptr) return list2;
        if (list2 == nullptr) return list1;
 
        // 比较大小后将当前较小节点作为头节点返回
        // 然后将它们链接起来
        if (list1->val < list2->val)
        {
            list1->next = dfs(list1->next, list2);
            return list1;   
        }
        else
        {
            list2->next = dfs(list1, list2->next);
            return list2; 
        }
    }
};

3. 反转链表

题目链接：206. 反转链表 - 力扣（LeetCode）

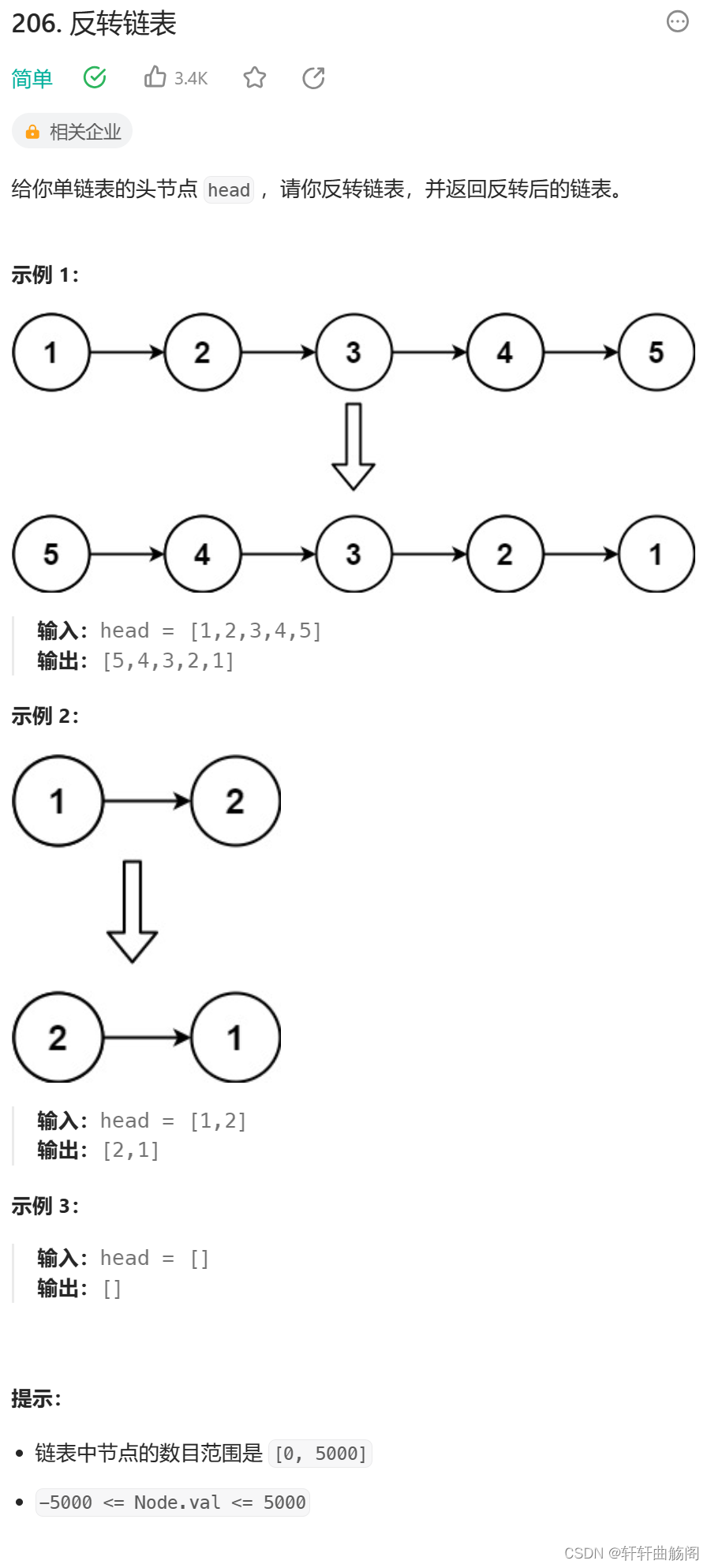
解析：

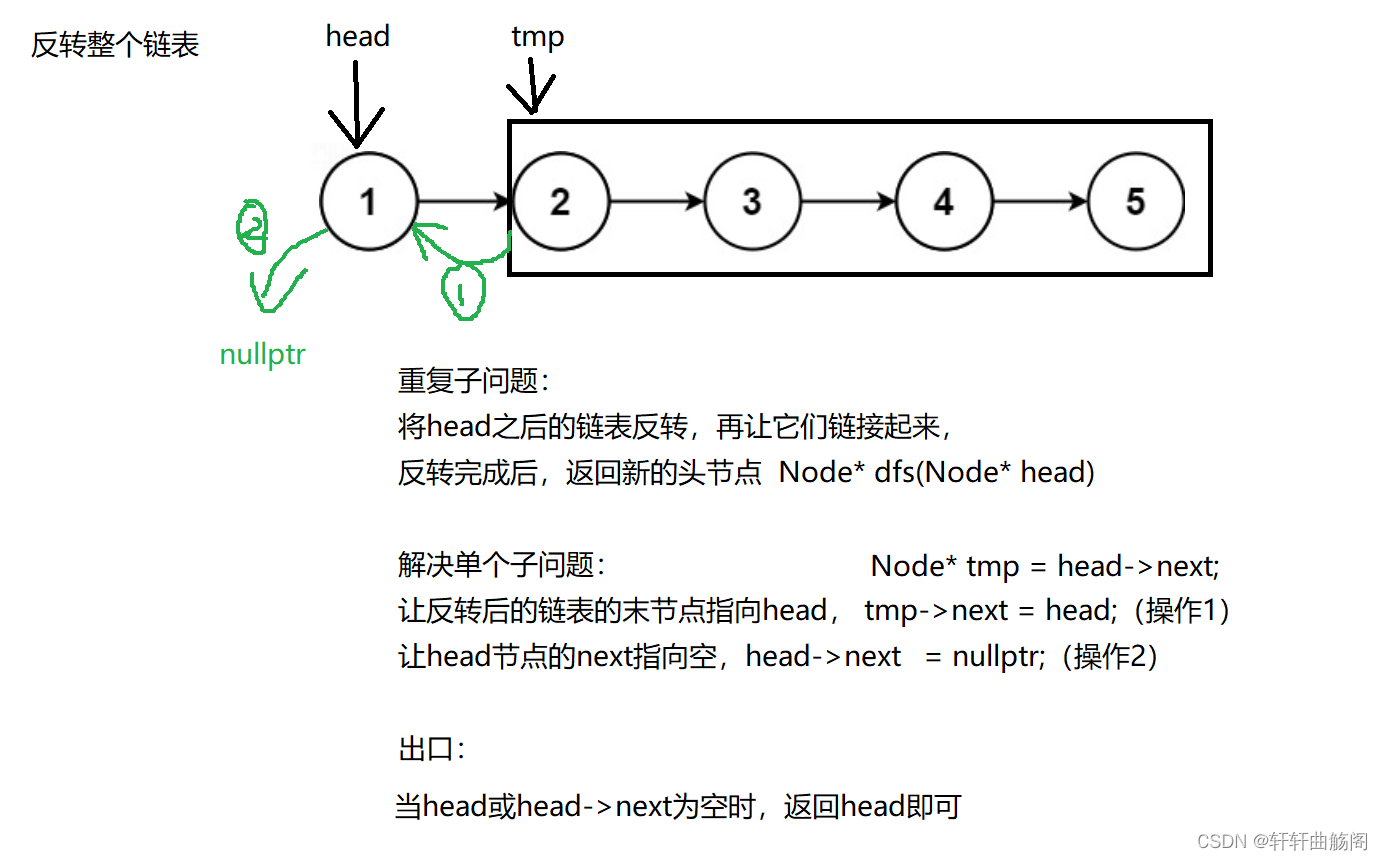
参考代码：

class Solution 
{
public:
    ListNode* reverseList(ListNode* head) 
    {
        // 出口
        if (head == nullptr || head->next == nullptr) return head;
 
        // 将当前节点之后的链表反转，并返回头节点
        ListNode* newhead = reverseList(head->next);
        // 反转之后让后面链表的next指向head
        head->next->next = head;
        // 再将head的next指向空
        head->next = nullptr;
 
        return newhead;
    }
};

4. 两两交换链表中的节点

题目链接：24. 两两交换链表中的节点 - 力扣（LeetCode）

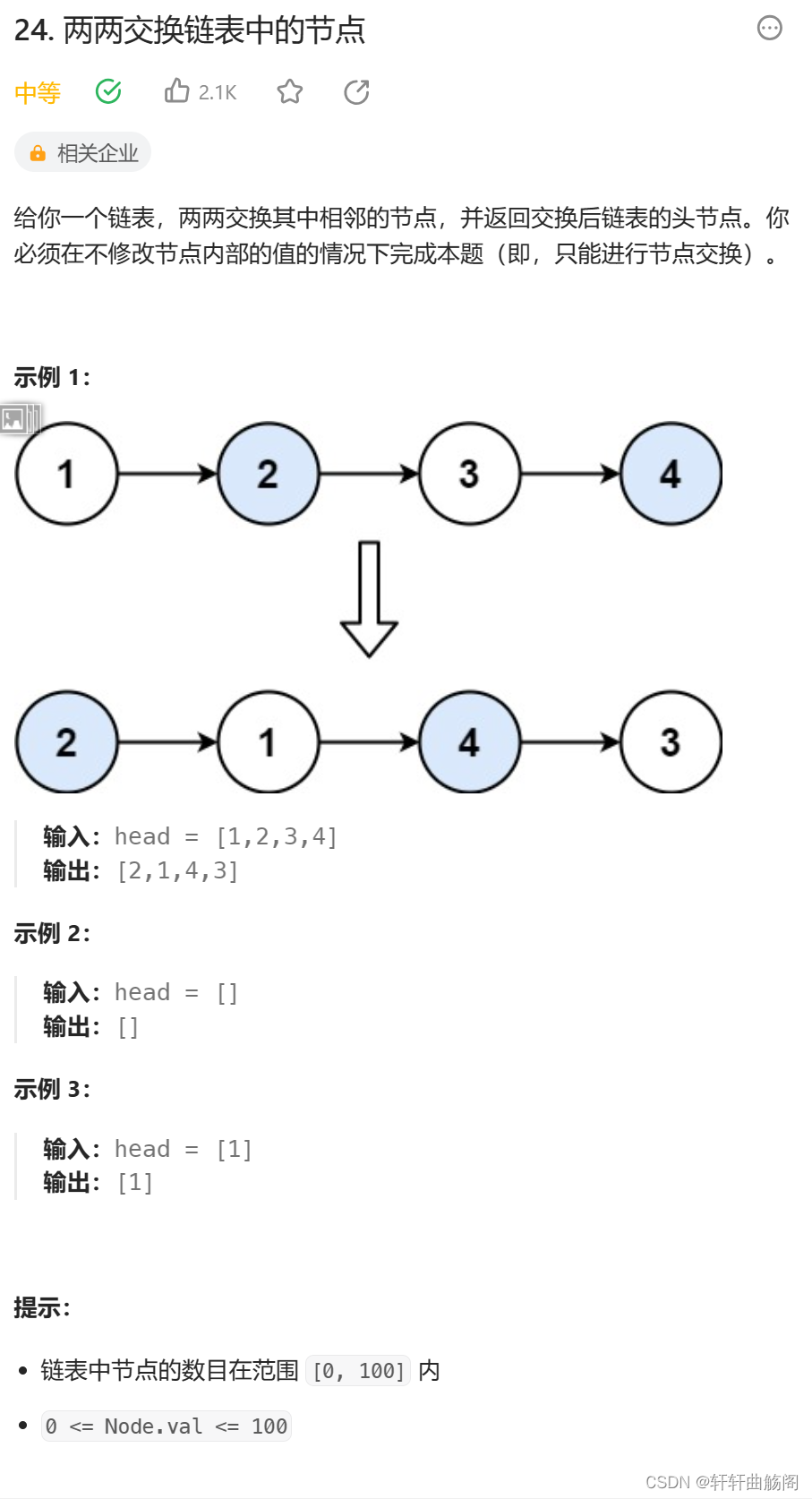
解析：

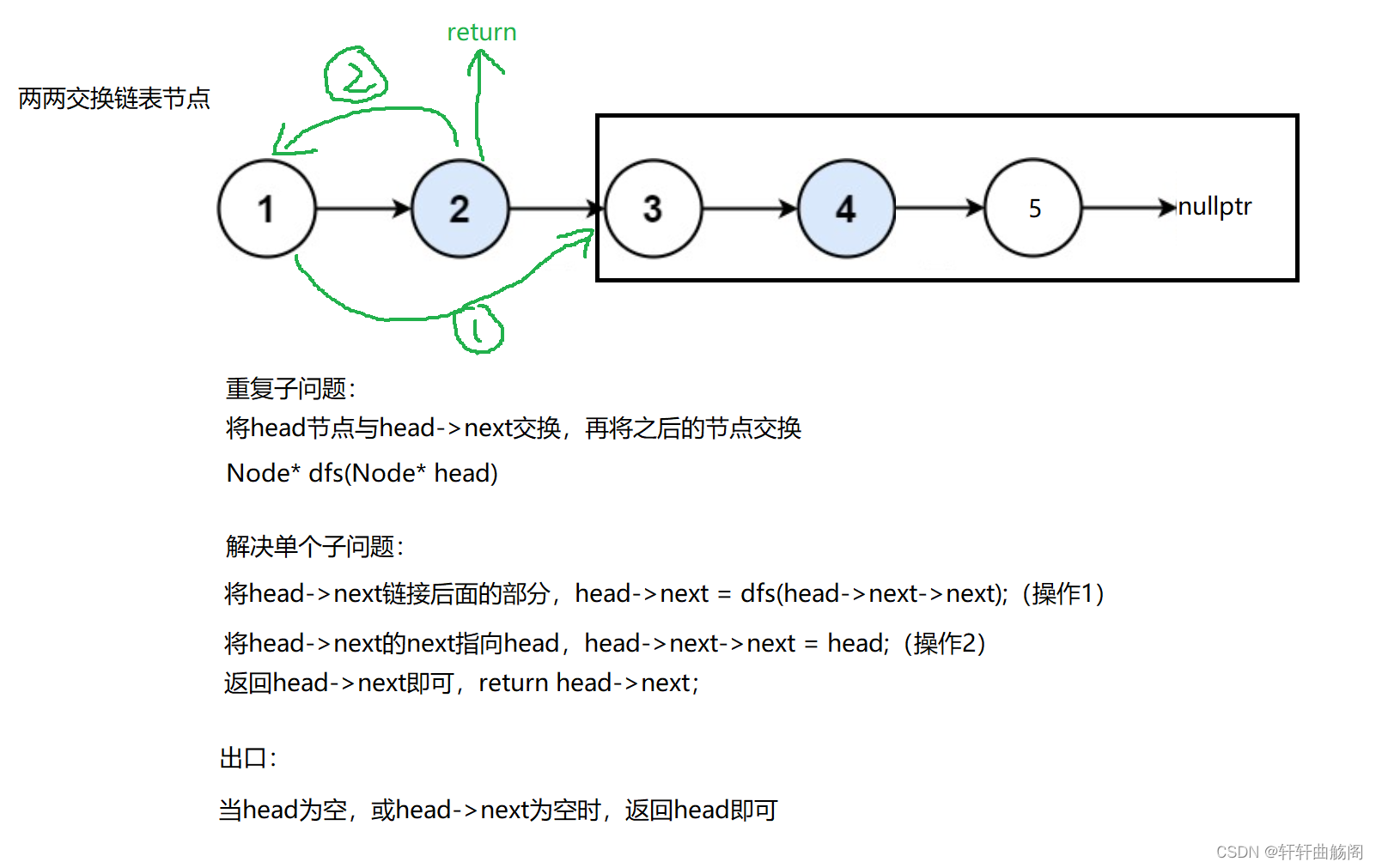
参考代码：

class Solution {
public:
    ListNode* dfs(ListNode* head)
    {
        // 出口
        if (head == nullptr || head->next == nullptr) return head;
 
        // 反转之后的链表并链接起来
        ListNode* next = head->next;
        head->next = dfs(next->next);
        next->next = head;
 
        return next;
    }
 
    ListNode* swapPairs(ListNode* head)
    {
        ListNode* newnode = dfs(head);
 
        return newnode;
    }
};

5. Pow(x, n) —— 快速幂 

题目链接：50. Pow(x, n) - 力扣（LeetCode）

解析：

参考代码：

class Solution {
public:
    double dfs(double x, int n)
    {
        if (n == 0) return 1;
 
        double tmp = dfs(x, n/2);
 
        return n % 2 == 0 ? tmp * tmp : tmp * tmp * x;
    } 
 
    double myPow(double x, int n) 
    {
        int flag = 0;
        long long num = n;
        if (n < 0) 
        {
            flag = 1;
            num *= -1;
        }
        double ret = dfs(x, n);
 
        return flag == 1 ? 1.0/ret : ret;
    }
};

注：在这里因为n可能会取到INT_MIN，将其取负时会导致int类型的变量储存不下，因此需要long long类型来储存 。

②二叉树专题

1. 计算布尔⼆叉树的值

题目链接：2331. 计算布尔二叉树的值 - 力扣（LeetCode）

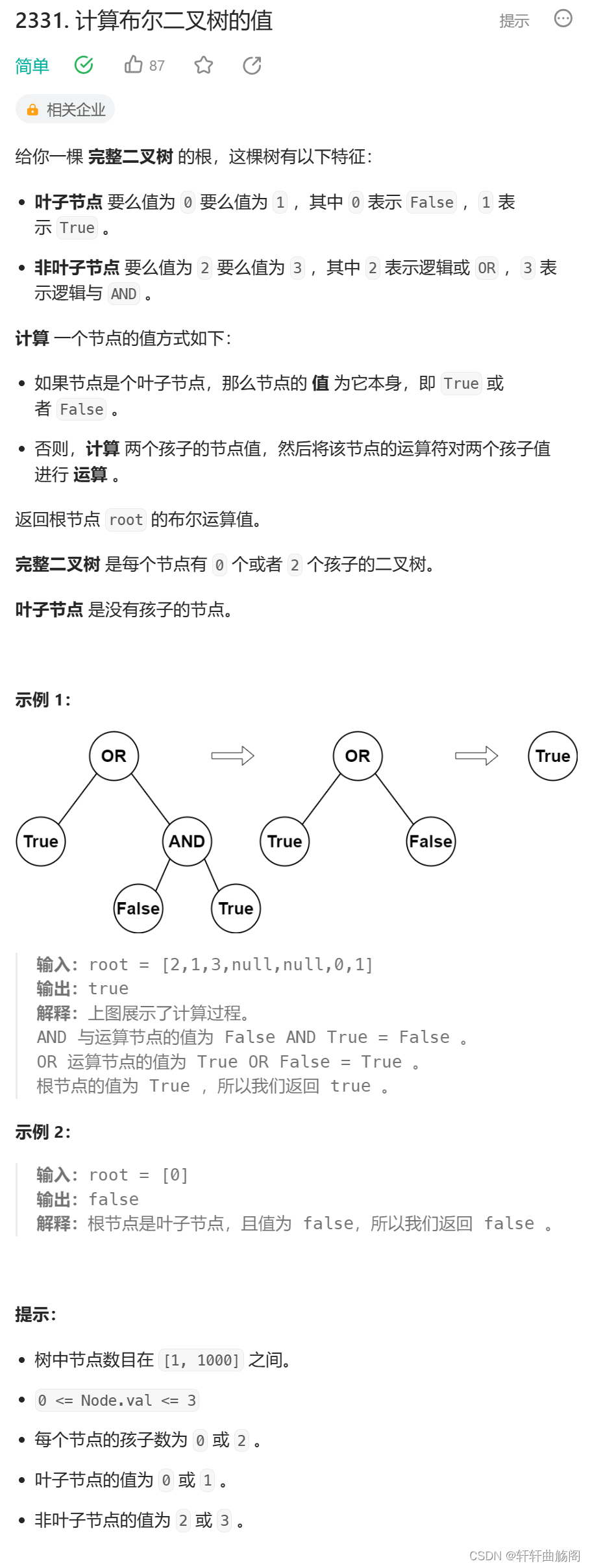
解析：

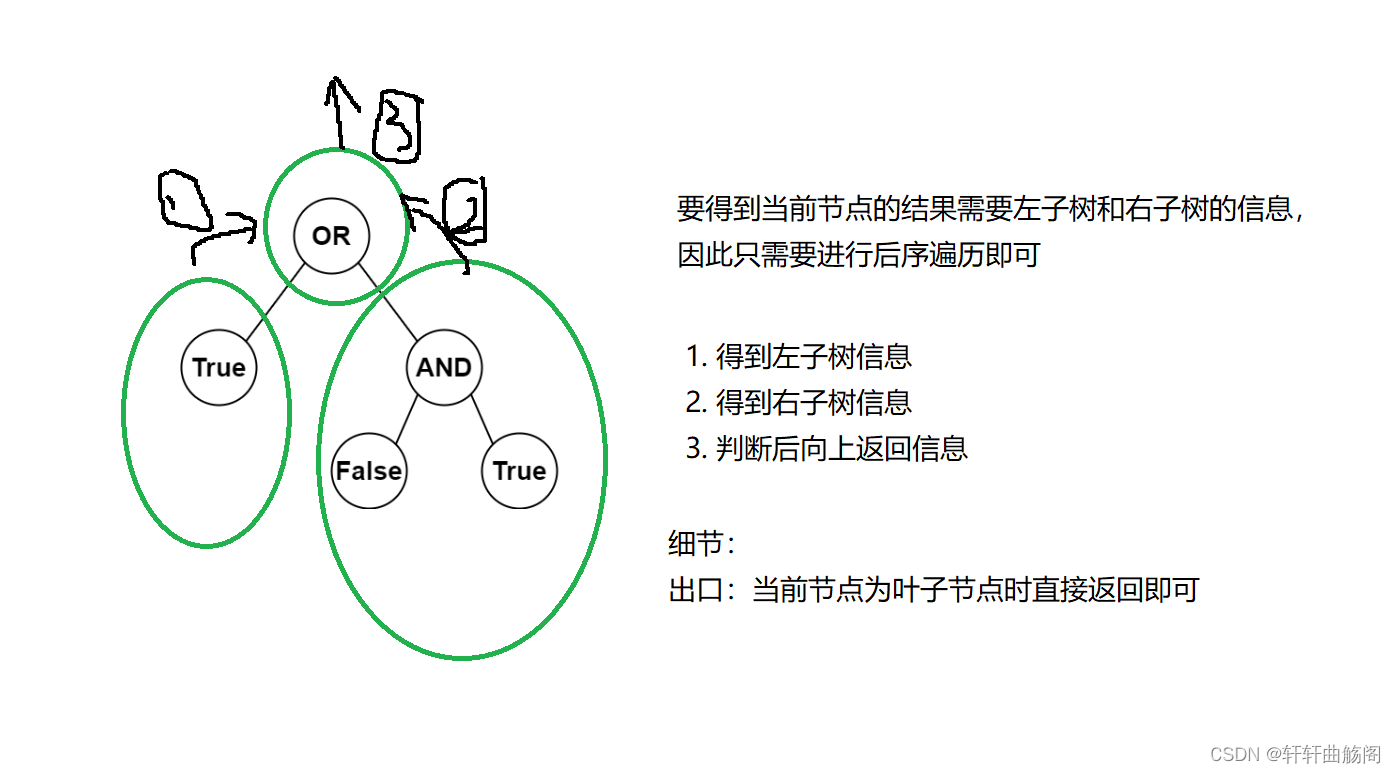
参考代码：

class Solution
{
public:
    bool evaluateTree(TreeNode* root)
    {
        if (root->left == nullptr && root->right == nullptr) return root->val;
 
        bool left = evaluateTree(root->left);
        bool right = evaluateTree(root->right);
 
        return root->val == 2 ? left || right : left && right;
    }
};

2. 求根节点到叶节点数字之和

题目链接：129. 求根节点到叶节点数字之和 - 力扣（LeetCode）

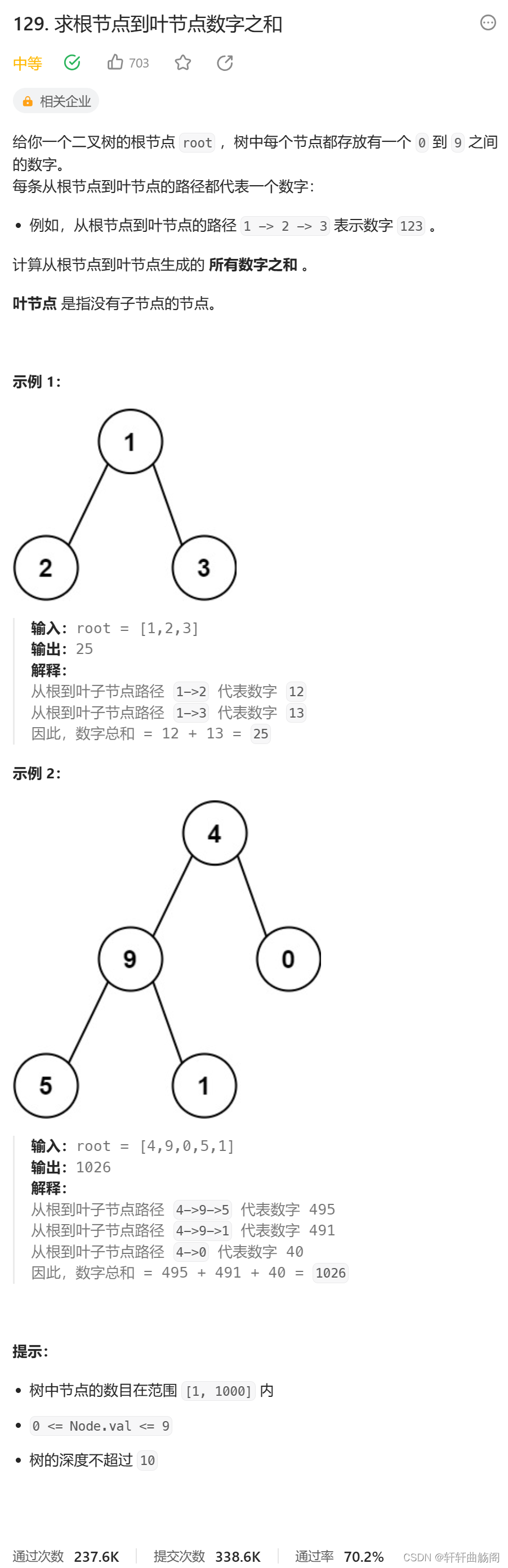
解析：

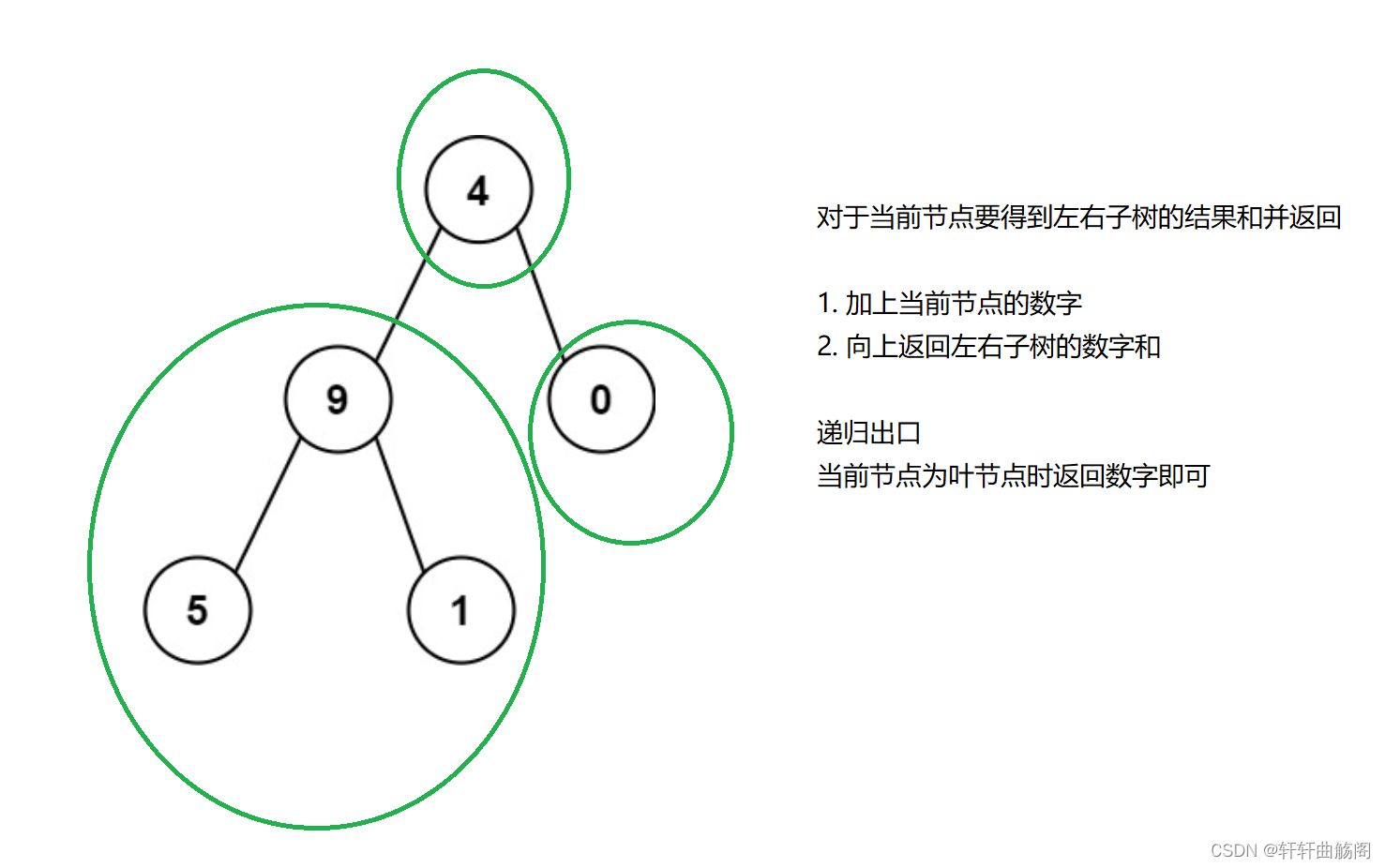
参考代码：

class Solution
{
public:
    int dfs(TreeNode* root, int prev)
    {
        prev = prev * 10 + root->val;
        if (root->left == nullptr && root->right == nullptr) return prev;
 
        int res = 0;
        if (root->left) res += dfs(root->left, prev);
        if (root->right) res += dfs(root->right, prev);
 
        return res;
    }
 
    int sumNumbers(TreeNode* root)
    {
        return dfs(root, 0);
    }
};

3. 二叉树剪枝

题目链接：814. 二叉树剪枝 - 力扣（LeetCode）

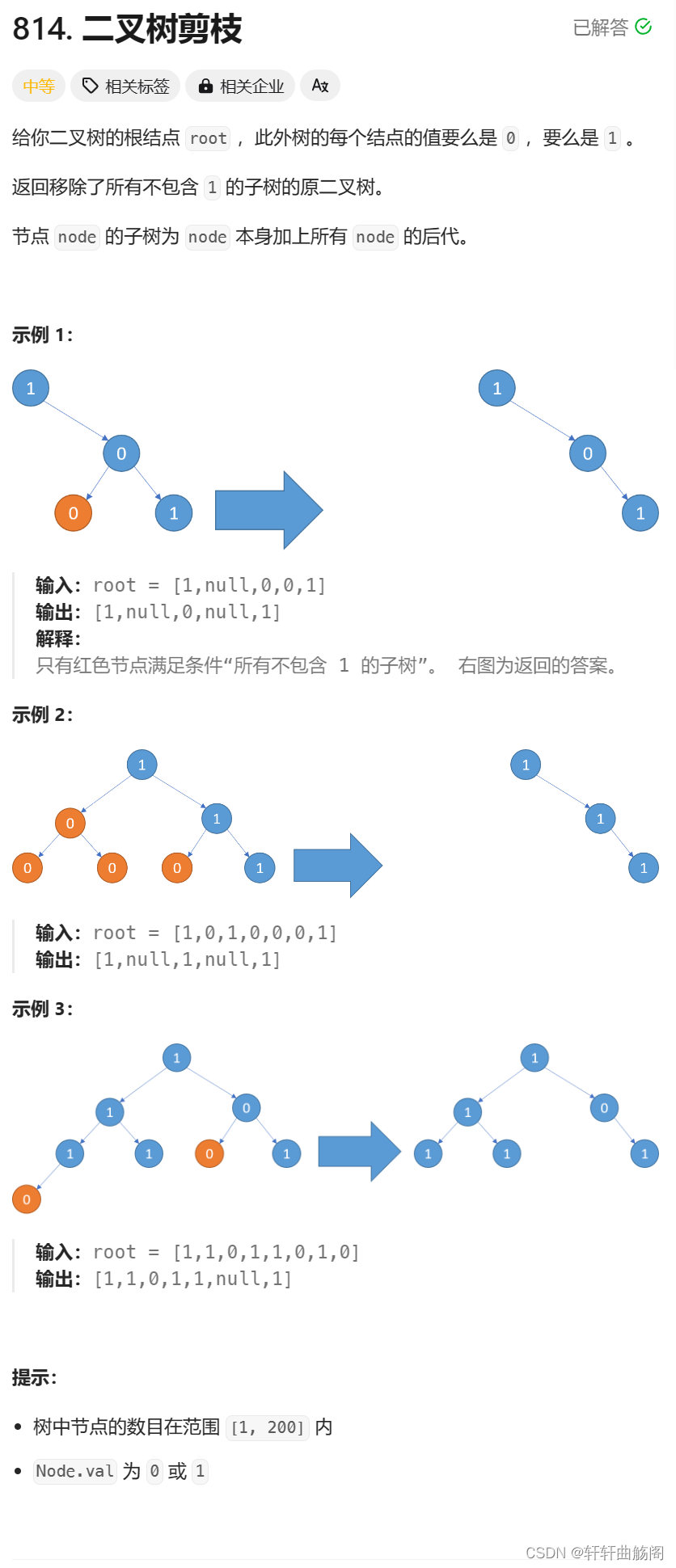
解析：分析题目，我们使用一个dfs函数，它的作用是能对当前二叉树进行剪枝操作，我们细分下来，就是对当前节点的左右节点分别进行剪枝操作，整体框架为

{
    // 出口
    
    root->left = dfs(root->left);
    root->right = dfs(root->right);
 
    // 具体实现
}

剪枝的具体情况应该是当左右子树均为空(nullptr)，且当前子树的val为0时，返回nullptr，其他情况返回root即可，代码实现如下

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution 
{
public:
    TreeNode* pruneTree(TreeNode* root) 
    {
        if (root == nullptr) return nullptr;
 
        root->left = pruneTree(root->left);
        root->right = pruneTree(root->right);
        if (root->left == nullptr && root->right == nullptr && root->val == 0) return nullptr;
 
        return root;
    }
};

4. 验证二叉搜索树

题目链接：98. 验证二叉搜索树 - 力扣（LeetCode）

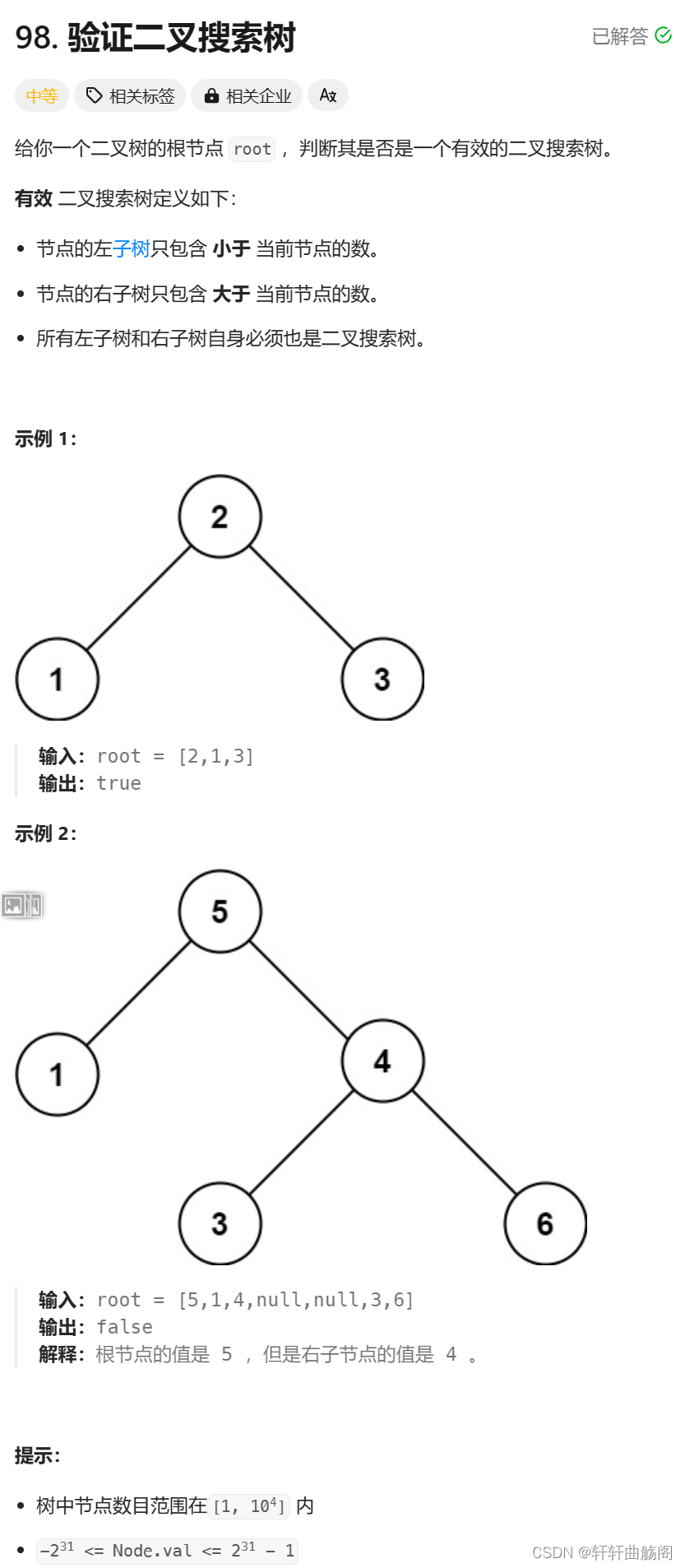
解析：分析一下题目，我们要想验证整棵树是否为二叉搜索树，只需验证它的左子树是否是二叉搜索树且值均小于当前节点，再验证它的右子树是否是二叉搜索树且值均大于当前节点，我们可以将验证右子树的过程拆解成验证右子树中的所有左子树是否合法，因此我们可以得到如下代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution 
{
public:
    long long prev = LONG_LONG_MIN;
 
    bool isValidBST(TreeNode* root) 
    {
        if (root == nullptr) return true;
 
        bool left = isValidBST(root->left);
        if (left == false) return false;
        if (prev >= root->val) return false;
        prev = root->val;
        bool right = isValidBST(root->right);
 
        return left && right;
    }
};

5. 二叉搜索树中第K小的元素

题目链接：230. 二叉搜索树中第K小的元素 - 力扣（LeetCode）

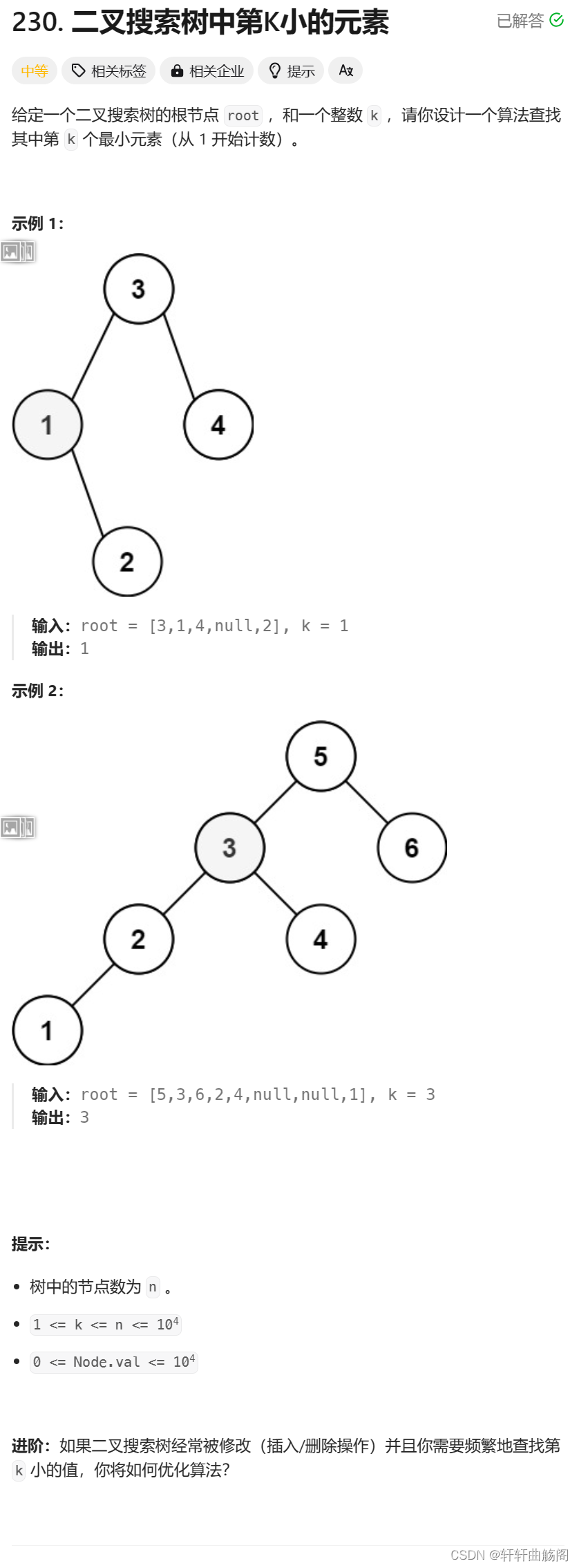
解析：分析题目，我们可以创建两个全局变量分别标识最后结果ret和当前是第几个最小元素count，我们可以先找到最小元素，即最左的节点，找到后依次向后查找，每一次查找count--，直到count减到0时，就是我们要找到的元素，代码如下

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution 
{
public:
    int count = 0;
    int ret = 0;
 
    int kthSmallest(TreeNode* root, int k) 
    {
        count = k;
 
        inorder(root);
 
        return ret;
    }
 
    void inorder(TreeNode* root)
    {
        if (root == nullptr) return;
        if (count == 0) return;
 
        inorder(root->left);
        count--;
        if (count == 0) ret = root->val;
        inorder(root->right);
    }
};

6. 二叉树的所有路径

题目链接：257. 二叉树的所有路径 - 力扣（LeetCode）

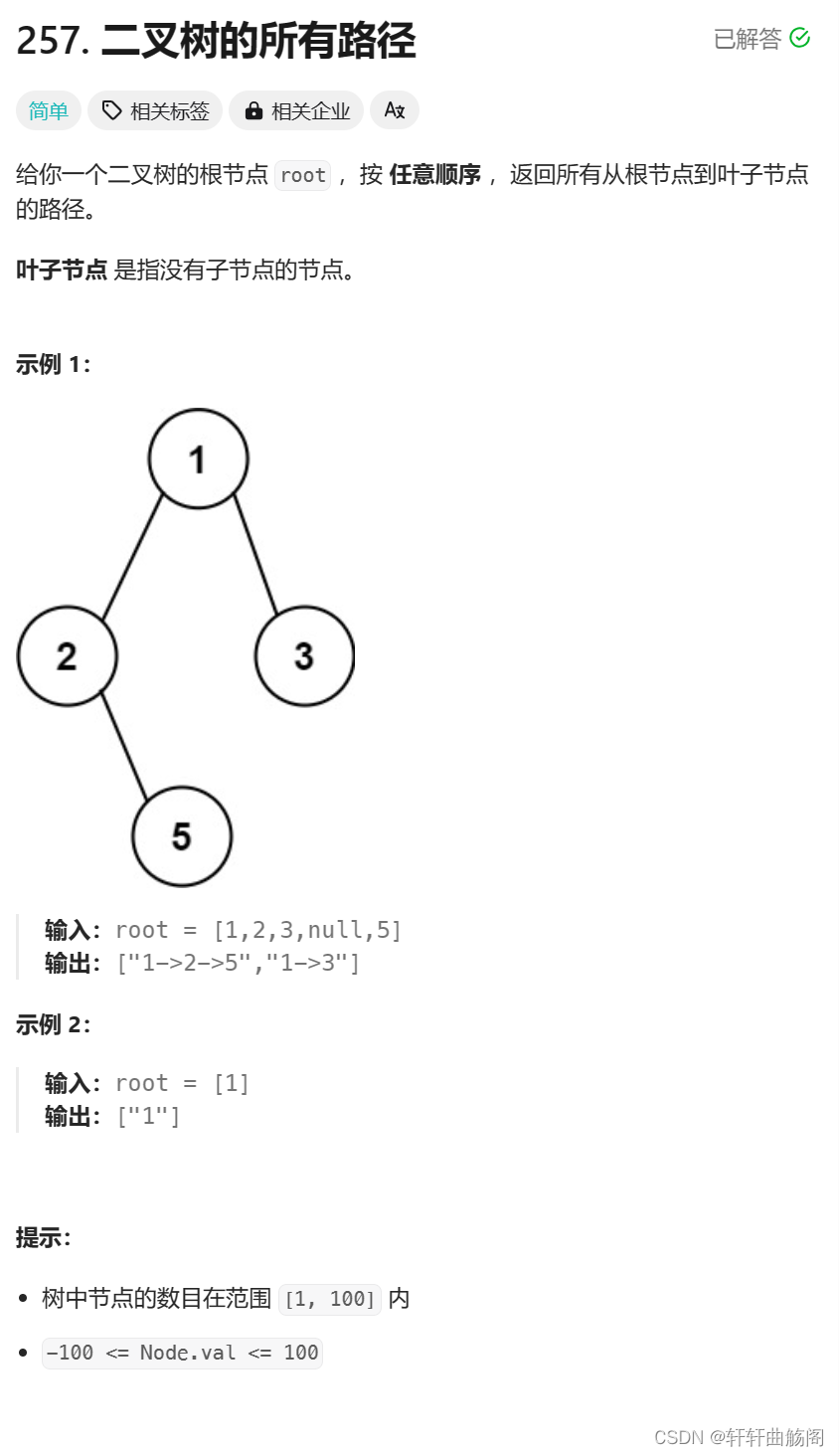
解析：分析题目我们可以发现，这道题要求的是找出所有的路径，因此我们需要一个全局变量path（或作为参数传递）来帮我们记录路径，需要注意的是当我们遍历完一条路径后，需要向上回溯，此时参数自然而然的就能做到回溯，而全局变量需要我们手动操作，在这里我们举例参数传递，代码如下

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution 
{
public:
    vector<string> res;
    vector<string> binaryTreePaths(TreeNode* root) 
    {
        string path;
        dfs(root, path);
 
        return res;
    }
 
    void dfs(TreeNode* root, string path)
    {
        if (root == nullptr) return;
 
        path += to_string(root->val);
        if (root->left == nullptr && root->right == nullptr) res.push_back(path);
        path += "->";
        dfs(root->left, path);
        dfs(root->right, path);
    }
};

③回溯与剪枝

1. 全排列

题目链接：46. 全排列 - 力扣（LeetCode）

解析：在这里我们可以总结出解决这种递归类型题目的通用解法：

1. 根据题意，画出一棵决策树（越详细越好）

2. 根据决策树，设计具体的代码，如：

①设计好全局变量

②设计dfs递归函数：仅关心某一个节点在干什么

③回溯处理

④剪枝处理

⑤递归函数的出口

分析一下这道题，我们可以画出如下的决策树

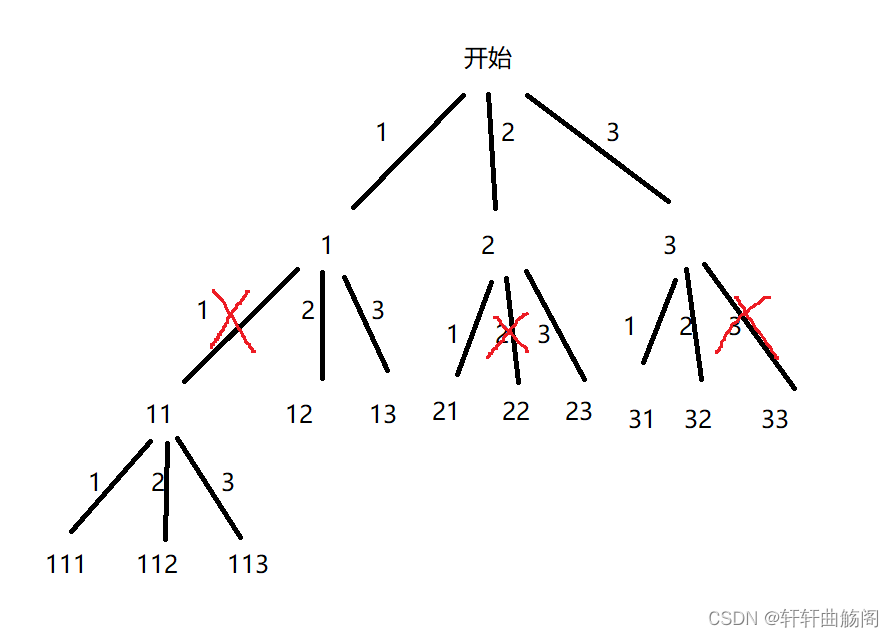
根据决策树，我们定义void dfs(vector<int> nums)来传入nums原数组，可以设计一个vector<int> path来记录每个路径的结果，定义bool check[7]来表示当前位置的数字是否已经使用过，vector<vector<int>> res来表示最终结果，在dfs函数中定义下标从0开始遍历数组，将每个没有使用过的数加入到path中，并将check[i]修改为true，在path的长度 == nums的长度时，将path插入到res中并停止递归，这之后进行回溯处理，即path.pop_back()，再将check[i]修改为false，进入下一个路径中，最终dfs函数结束时res中已经保存好了所有结果，返回即可，代码如下

class Solution 
{
public:
    vector<vector<int>> res;
    vector<int> path;
    bool check[7];
 
    vector<vector<int>> permute(vector<int>& nums) 
    {
        dfs(nums);
        return res;
    }
 
    void dfs(vector<int>& nums)
    {
        if (path.size() == nums.size())
        {
            res.push_back(path);
            return;
        }
 
        int n = nums.size();
        for (int i = 0; i < n; i++)
        {
            if (check[i] == false)
            {
                path.push_back(nums[i]);
                check[i] = true;
                dfs(nums);
                path.pop_back();
                check[i] = false;
            }
        }
    }
};

2. 子集

题目链接：78. 子集 - 力扣（LeetCode）

解析：我们画出决策树有

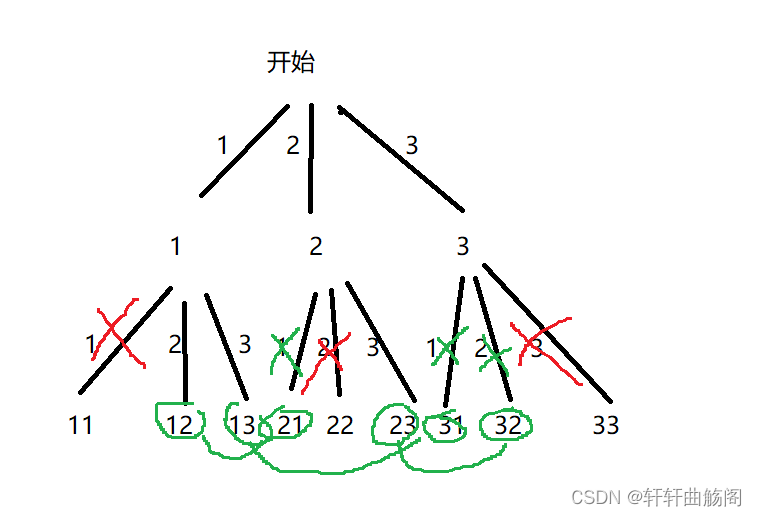
在这里我们稍加分析可以发现每一次想要递归到下一层需要传入比自己大的下标的数字，因此可以定义dfs函数 void dfs(vector<int> nums, int i)这里的i表示当前数字所处的下标，再定义一个res与path全局变量，可以看到，每一个可行的结点都是一个子集，因此我们需要将每个可行节点加入到res中，当i == nums.size()的时候停止递归，由于在设计dfs函数的时候我们已经考虑到了剪枝，因此我们只需要做回溯处理即可，即在递归前将当前path入res，在递归结束后使path.pop_back()，最终经历完dfs函数后，res存放了最后的结果，代码如下

class Solution 
{
public:
    vector<vector<int>> res;
    vector<int> path; 
 
    vector<vector<int>> subsets(vector<int>& nums) 
    {
        dfs(nums, 0);
        return res;
    }
 
    void dfs(vector<int>& nums, int pos)
    {
        res.push_back(path);
 
        for (int i = pos; i < nums.size(); i++)
        {
            path.push_back(nums[i]);
            dfs(nums, i+1);
            path.pop_back();
        }
    }
};

除了上面的决策树以外，我们还可以根据选或不选来划出决策树，即

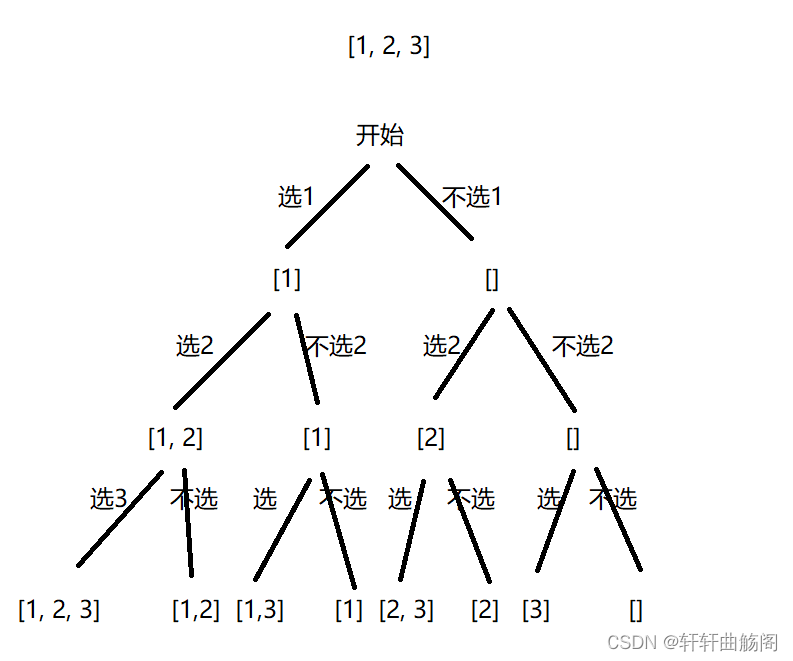
根据决策树，我们可以设计dfs函数 void dfs(vector<nums>, int i)其中i表示待选元素的下标，我们需要创建path和res分别统计路径及结果，遍历数组元素并将选与不选的情况分别加入到path中，需要注意的是在回溯时，我们需要对path进行push与pop的操作，当path.size() == nums.size()时递归结束，代码如下

class Solution 
{
public:
    vector<vector<int>> res;
    vector<int> path;
 
    vector<vector<int>> subsets(vector<int>& nums) 
    {
        dfs(nums, 0);
        return res;
    }
 
    void dfs(vector<int>& nums, int i)
    {
        if (i == nums.size())
        {
            res.push_back(path);
            return;
        }
 
        dfs(nums, i+1);
 
        path.push_back(nums[i]);
        dfs(nums, i+1);
        path.pop_back();
    }
};

④综合训练

1. 找出所有子集的异或总和再求和

题目链接：1863. 找出所有子集的异或总和再求和 - 力扣（LeetCode）

解析：分析题意，我们首先要得到所有的子集，我们可以使用先前的代码得到所有的子集，这之后统计每个子集中的异或值并相加，代码如下

class Solution 
{
public:
    int ret;
    vector<vector<int>> elem;
    vector<int> path;
 
    int subsetXORSum(vector<int>& nums) 
    {
        dfs(nums, 0);
        for (auto& v : elem)
        {
            int tmp = 0;
            for (auto& e : v) tmp ^= e;
            ret += tmp;
        }
 
        return ret;
    }
 
    void dfs(vector<int>& nums, int pos)
    {
        elem.push_back(path);
        for (int i = pos; i < nums.size(); i++)
        {
            path.push_back(nums[i]);
            dfs(nums, i+1);
            path.pop_back();
        }
    }
};

2. 全排列Ⅱ

题目链接：47. 全排列 II - 力扣（LeetCode）

解析：这道题的解决思路与全排列的想法大同小异，至于去重我们可以使用set容器来帮助我们去重，最终代码如下

class Solution 
{
public:
    set<vector<int>> res;
    vector<int> path;
    bool check[9];
 
    vector<vector<int>> permuteUnique(vector<int>& nums) 
    {
        vector<vector<int>> ret;
 
        dfs(nums);
        for (auto& v : res) ret.push_back(v);
 
        return ret;
    }
 
    void dfs(vector<int>& nums)
    {
        if (path.size() == nums.size()) res.insert(path);
 
        for (int i = 0; i < nums.size(); i++)
        {
            if (check[i] == false) 
            {
                path.push_back(nums[i]);
                check[i] = true;
                dfs(nums);
                path.pop_back();
                check[i] = false;
            }
        }
    }
};

3. 电话号码的字母组合

题目链接：17. 电话号码的字母组合 - 力扣（LeetCode）

解析：根据题意，我们可以画出如下决策树

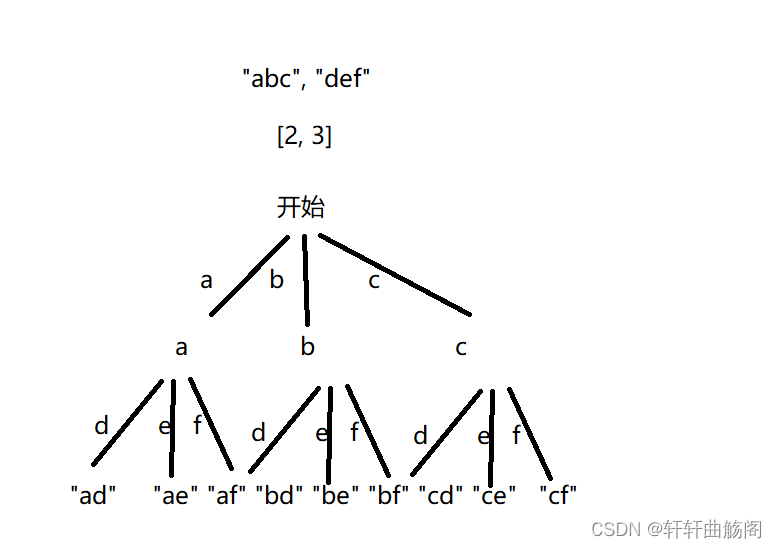
我们可以先设立一个全局数组来映射数字与字符串的关系，可以设计dfs为 void dfs(vector<nums>)， 随后将每个数字对应的字符串中的字符插入到path中，当path.size( ) == nums.size()时，插入res中并结束递归，由于是全局的path所以需要我们手动地对path进行push与pop操作，代码如下

class Solution 
{
public:
    vector<string> letter = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
    vector<string> res;
    string path;
    int n;
 
    vector<string> letterCombinations(string digits) 
    {
        n = digits.size();
        if (n == 0) return res;
        dfs(digits);
 
        return res;
    }
 
    void dfs(string digits)
    {
        if (path.size() == n) 
        {
            res.push_back(path);
            return;
        }
 
        int first = digits[0] - '0';
        digits.erase(0, 1);
        string tmp = letter[first];
        for (int i = 0; i < tmp.size(); i++)
        {
            path += tmp[i];
            dfs(digits);
            path.pop_back();
        }
    }
};

4. 括号生成

题目链接：22. 括号生成 - 力扣（LeetCode）

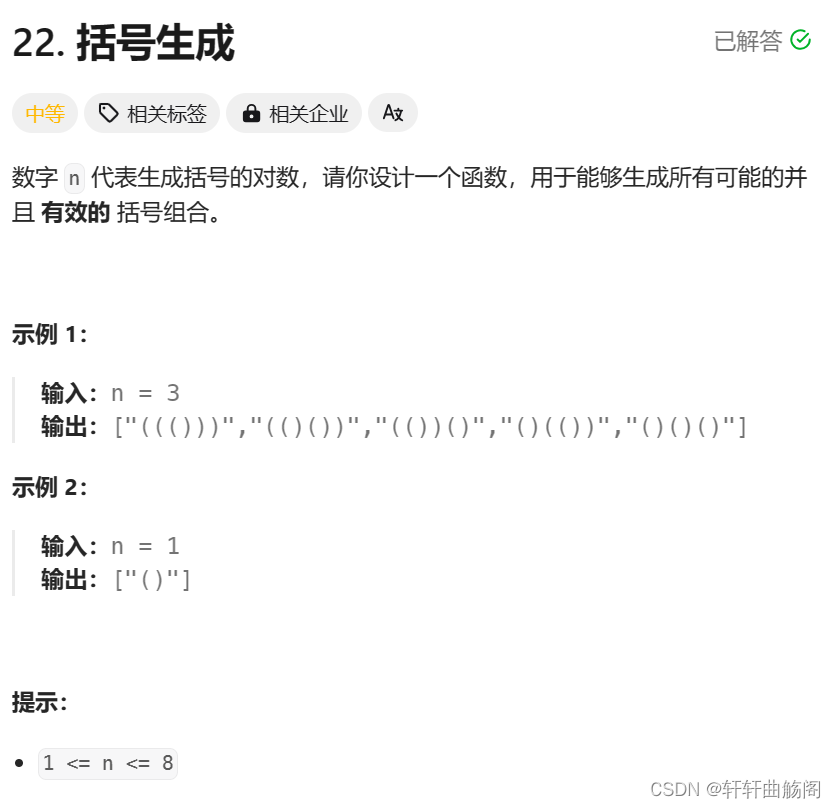
解析：分析这道题我们可以画出如下的决策树

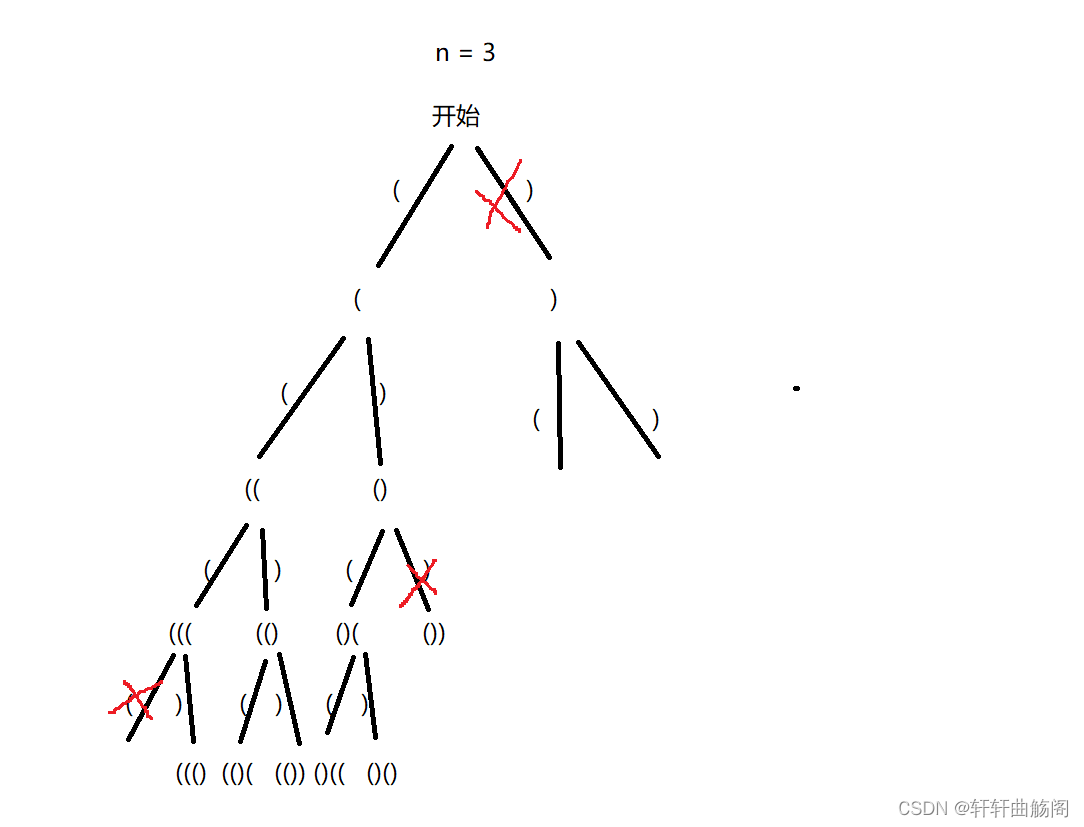
根据决策树，我们可以设计dfs函数 void dfs(int n) 其中n表示要生成的括号总对数，而全局函数中除了常规的path与res以外，我们还需要定义left与right来分别表示当前左右单括号的个数，根据决策树我们可以看到，在每次插入后，如果right > left时括号违法，此时递归回溯，而如果left > n时括号也违法，此时递归回溯，其余情况均合法，当left == right 且 left == n时，将path插入到res中，并结束递归，代码如下

class Solution 
{
public:
    vector<string> res;
    string path;
    int left = 0, right = 0;
 
    vector<string> generateParenthesis(int n) 
    {
        dfs(n);
 
        return res;
    }
 
    void dfs(int n)
    {
        if (left > n || right > left) return;
        if (left == right && left == n)
        {
            res.push_back(path);
            return;
        }
 
        path += '(';
        left++;
        dfs(n);
        path.pop_back();
        left--;
 
        right++;
        path += ')';
        dfs(n);
        right--;
        path.pop_back();
    }
};

5. 组合

题目链接：77. 组合 - 力扣（LeetCode）

解析：我们根据题目可以画出如下决策树

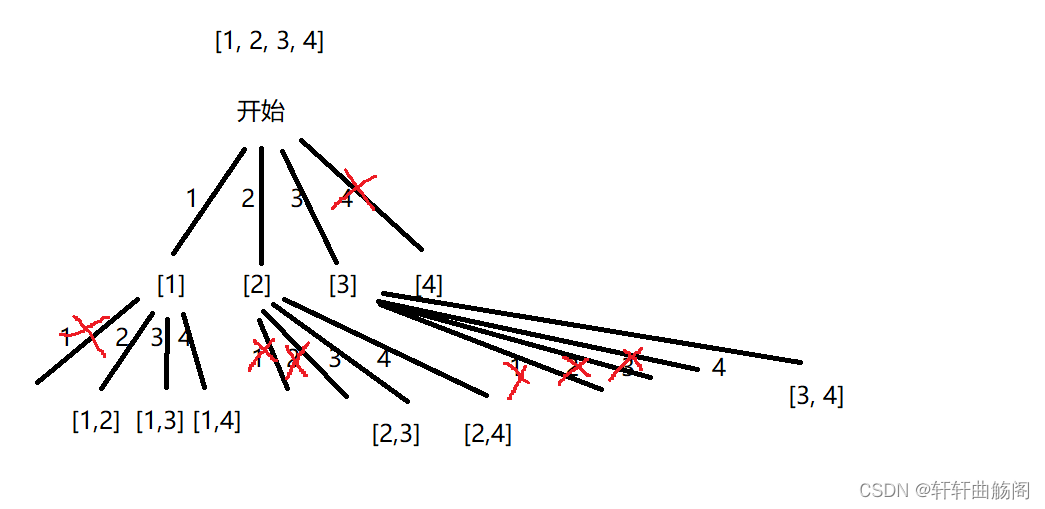
根据决策树，我们可以定义全局变量res与path分别记录结果与路径，dfs函数： void dfs(vector<nums>, int k)即可，在遍历时每次只需要从i之后的下标开始遍历数组，在递归前后要对path手动修改，当path.size() == k时，将path插入到res并结束递归，代码如下

class Solution 
{
public:
    vector<vector<int>> res;
    vector<int> path;
 
    vector<vector<int>> combine(int n, int k) 
    {
        dfs(n, k);
 
        return res;
    }
 
    void dfs(int n, int k)
    {
        if (path.size() == k)
        {
            res.push_back(path);
            return;
        }
 
        for (int i = 1; i <= n; i++)
        {
            if (path.empty() || path.back() < i)
            {    
                path.push_back(i);
                dfs(n, k);
                path.pop_back();
            }
        }
    }
};

6. 目标和

题目链接：494. 目标和 - 力扣（LeetCode）

解析：根据题目我们可以画出决策树

根据决策树，我们可以定义全局变量ret表示最终满足条件的个数，num表示当前数值的大小，target表示要求寻找的数值大小，dfs函数：void dfs(vector<int>, int count)其中count表示数组下标同时标识当前递归是否应该结束，每次递归要先加上nums[count]在回溯后应该再减去它，再减去nums[count]在回溯后再加上它，当count == nums.size()时判断当前数值是否等于target，相等则ret++并结束递归，否则直接结束递归，代码如下

class Solution 
{
public:
    int ret;
    long long num;
    int target;
 
    int findTargetSumWays(vector<int>& nums, int _target) 
    {
        num = 0;target = _target;ret = 0;
        dfs(nums, 0);
 
        return ret;
    }
 
    void dfs(vector<int>& nums, int count)
    {
        if (count == nums.size())
        {
            if (target == num) ret++;
            return;
        }
 
        num += nums[count];
        dfs(nums, count+1);
        num -= nums[count];
 
        num -= nums[count];
        dfs(nums, count+1);
        num += nums[count];
    }
};

7. 组合总和

题目链接：39. 组合总和 - 力扣（LeetCode）

解析：分析题目我们可以画出如下决策树

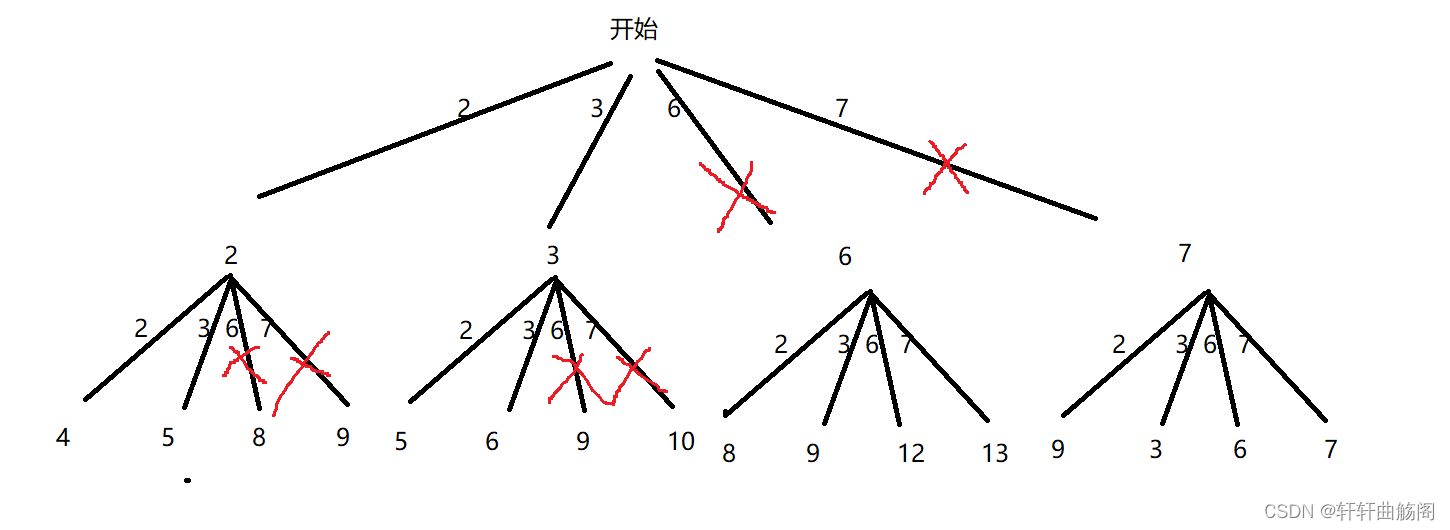
根据决策树，我们需要使用一个全局变量path记录路径，res记录最终结果，target标识最终要寻找的目标值，dfs函数：void dfs(vector<int> nums, int sum)其中sum表示当前路径的总和，在递归过程中一旦当前路径总和sum >= target 在判断是否等于target后将path插入res并结束递归，其他情况则直接结束递归，此外我们在调用dfs函数后要回溯sum，代码如下

class Solution
{
public:
    vector<vector<int>> res;
    int target;
    vector<int> path;
 
    vector<vector<int>> combinationSum(vector<int>& candidates, int _target) 
    {
        target = _target;
        dfs(candidates, 0);
 
        return res;
    }
 
    void dfs(vector<int>& candidates, int sum)
    {
        if (sum >= target)
        {
            if (sum == target) res.push_back(path);
            return;
        }
 
        for (int i = 0; i < candidates.size(); i++)
        {
            if (path.empty() || path.back() <= candidates[i])
            {
                path.push_back(candidates[i]);
                dfs(candidates, sum + candidates[i]);
                path.pop_back();
            }
        }
    }
};

8. 字母大小写全排列

题目链接：784. 字母大小写全排列 - 力扣（LeetCode）

解析：根据题目有

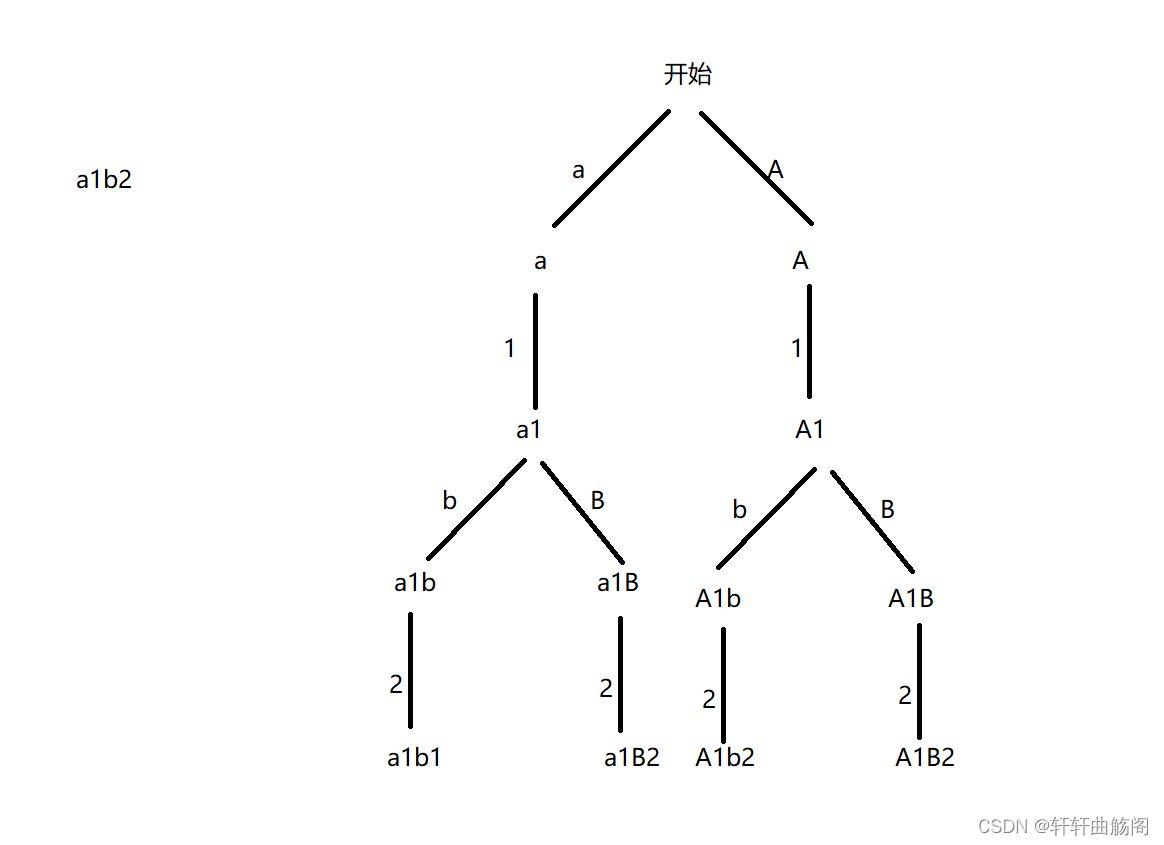
根据决策树，我们可以设计path，res与n（n表示string的长度），dfs函数：void dfs(string s, int pos, string path)其中pos表示当前指向元素的下标，path表示当前路径，每次当当前元素为小写字母或大写字母时，要同时对小写和大写字符同时进行递归，而遇见数字时直接尾插即可，当path.size() == n时，将path插入res并结束递归，代码如下

class Solution 
{
public:
    vector<string> res;
    int n;
 
    vector<string> letterCasePermutation(string s) 
    {
        n = s.size();
        string path;
        dfs(s, 0, path);
 
        return res;
    }
 
    void dfs(string& s, int pos, string path)
    {
        if (path.size() == n)
        {
            res.push_back(path);
            return;
        }
 
        if (s[pos] >= 'a' && s[pos] <= 'z')
        {
            char up = s[pos] + 'Z' - 'z';
            dfs(s, pos + 1, path + s[pos]);
            dfs(s, pos + 1, path + up);
        }
        else if (s[pos] >= 'A' && s[pos] <= 'Z')
        {
            char low = s[pos] - 'Z' + 'z';
            dfs(s, pos + 1, path + s[pos]);
            dfs(s, pos + 1, path + low);
        }
        else
        {
            dfs(s, pos + 1, path + s[pos]);
        }
    }
};

9. 优美的排列

题目链接：526. 优美的排列 - 力扣（LeetCode）

⑤FloodFill算法

1. 图像渲染

题目链接：733. 图像渲染 - 力扣（LeetCode）

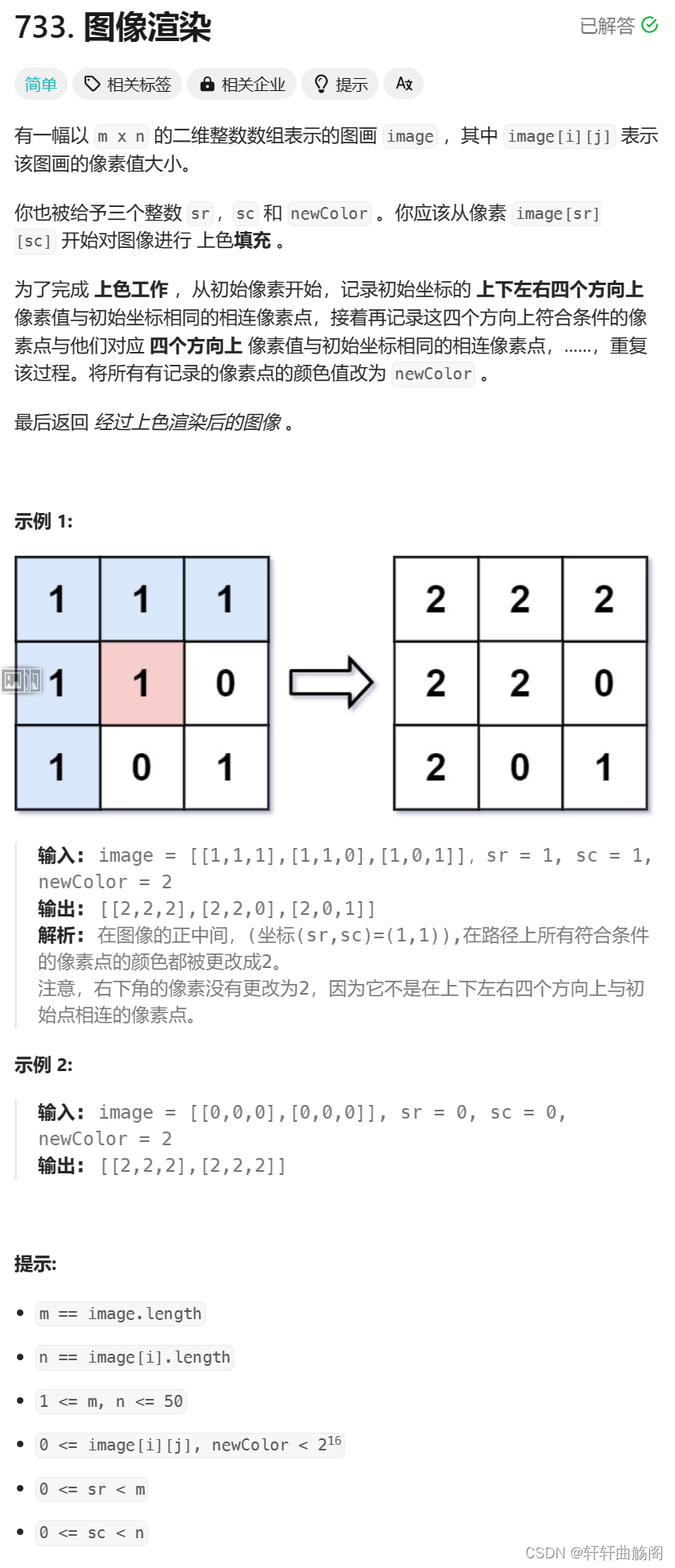
解析：分析题目，我们可以定义dfs函数：void dfs(vector<vector<int>>& image, int row, int col, int newcolor)，其中newcolor表示新的渲染颜色，在经历一次dfs后，将(row, col)与所有性质与其相同的图像均渲染成newcolor，最终代码如下

class Solution 
{
public:
    int dx[4] = {1,-1,0,0};
    int dy[4] = {0,0,1,-1};
    int m,n;
    bool check[51][51];
 
    vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) 
    {
        m = image.size(), n = image[0].size();
        dfs(image, sr, sc, color);
 
        return image;
    }
 
    void dfs(vector<vector<int>>& image, int row, int col, int color)
    {
        check[row][col] = true;
        for (int i = 0; i < 4; i++)
        {
            int x = row + dx[i], y = col + dy[i];
            if (x >= 0 && x < m && y >= 0 && y < n && check[x][y] == false && image[x][y] == image[row][col])
            {
                dfs(image, x, y, color);
            }
        }
        image[row][col] = color;
    }
};