安全路径 [容斥]_路径安全

$$安全路径$$

$最初想法$

感觉是树形dp, 一步错步步错 .
设 $F[i]$ 表示以 $i$ 点端点在其子树中有多少条符合条件的路径, 且当前枚举到了子树节点 $to$,

发现这样的状态只能 $O(N^2)$ 枚举根才能得出正确的答案 .

• 若边权为 ${}^{\prime }{b}^{\prime }$, 则 $Ans+=F[k]\ast F[to]$, $F[k]+=F[to]$
• 若边权为 ${}^{\prime }{r}^{\prime }$, 则 $Ans+=F[k]\ast size[to]$, $F[k]+=size[to]$.

然后就交上去了, 发现爆炸 .
原因是 题目中的三元组 之间的路径 才有限制(死在这里), 不一定成一条链, 可以是下图这个样子,

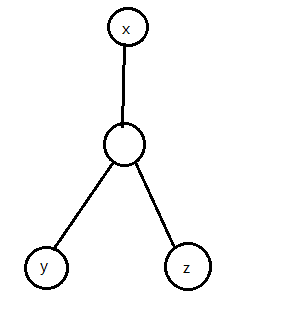
所以这个算法已废 .

样例真水

$正解部分$

可以容斥, 求出 危险的三元组 的个数,
危险的三元组点与点之间 存在 全 ${}^{\prime }{b}^{\prime }$ 路径,
所以求出所有蓝色的连通块大小 $S_i$,
$$Ans=C_N^3-\sum C_{S_i}^3-\sum C_{S_i}^2\ast (N-S_i)$$ .

十年OI一场空, 看错题目见祖宗 …

$实现部分$

若两个点有蓝边相连, 即可归入同一个连通块, 可以使用并查集实现 .

#include<bits/stdc++.h>
#define reg register

int read(){
        char c;
        int s = 0, flag = 1;
        while((c=getchar()) && !isdigit(c))
                if(c == '-'){ flag = -1, c = getchar(); break ; }
        while(isdigit(c)) s = s*10 + c-'0', c = getchar();
        return s * flag;
}

const int maxn = 50005;
const int mod = 1e9 + 7;

int N;
int F[maxn];
int fac[maxn];
int size[maxn];
int rev[maxn];

int Ksm(int a, int b){
	int s = 1;
	while(b){
		if(b & 1) s = 1ll*s*a % mod;
		a = 1ll*a*a % mod;
		b >>= 1;
	}
	return s;
}

int C(int n, int m){
        int t1 = fac[n];
        int t2 = 1ll*fac[n-m]*fac[m] % mod;
        return 1ll*t1*Ksm(t2, mod-2) % mod;
}

int Find(int x){ return F[x]==x?x:F[x]=Find(F[x]); }

int main(){
        N = read();
        for(reg int i = 1; i <= N; i ++) F[i] = i, size[i] = 1;
        for(reg int i = 1; i < N; i ++){
                char ch[2];
                int a = read(), b = read();
                scanf("%s", ch);
                if(ch[0] == 'b'){
                        int t1 = Find(a), t2 = Find(b);
                        if(t1 != t2) F[t2] = t1, size[t1] += size[t2];
                }
        }
        fac[0] = 1;
        for(reg int i = 1; i <= N; i ++) fac[i] = 1ll*fac[i-1]*i % mod;
        int Ans = C(N, 3);
        for(reg int i = 1; i <= N; i ++){
                if(Find(i) != i) continue ;
                if(size[i] >= 3) Ans = (1ll*Ans - C(size[i], 3) + mod) % mod;
                if(size[i] >= 2) Ans = (1ll*Ans - (1ll*C(size[i], 2)*(N-size[i])%mod) + mod) % mod;
        }
        printf("%d\n", Ans);
        return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62