字符匹配问题 -- 通配符匹配 && 正则表达式匹配_正则表达式 字符* 匹配问题

1. 通配符匹配

1.1 题目描述

给你一个输入字符串 (s) 和一个字符模式 (p) ，请你实现一个支持 '?' 和 '*' 匹配
规则的通配符匹配：
 '?' 可以匹配任何单个字符。
 '*' 可以匹配任意字符序列（包括空字符序列）。
判定匹配成功的充要条件是：字符模式必须能够 完全匹配 输入字符串（而不是部分匹配）。

示例1：

输入：s = "aa", p = "a"
输出：false
解释："a" 无法匹配 "aa" 整个字符串。

示例2：

输入：s = "aa", p = "*"
输出：true
解释：'*' 可以匹配任意字符串。

示例3：

输入：s = "cb", p = "?a"
输出：false
解释：'?' 可以匹配 'c', 但第二个 'a' 无法匹配 'b'。

1.2 算法原理

        根据经验，涉及到字符串的动态规划，我们的状态定义一般都是拿两个区间的子串或者子序列进行比较，所以此处的状态可以这样定义：

状态定义：dp[i][j] 表示：p[0,j] 区间内的子串能否匹配 s[0, i] 区间内的子串. 【true or false】

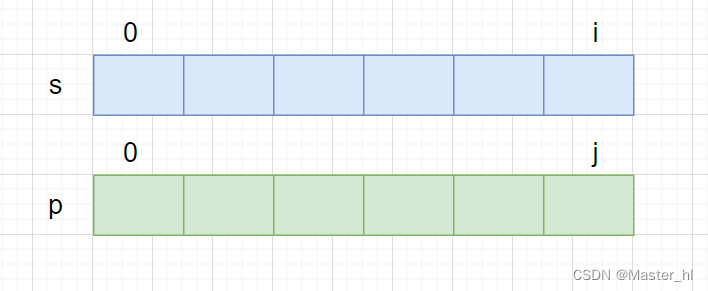
【推导状态转移方程】

根据最后一个位置的状况，分情况讨论：

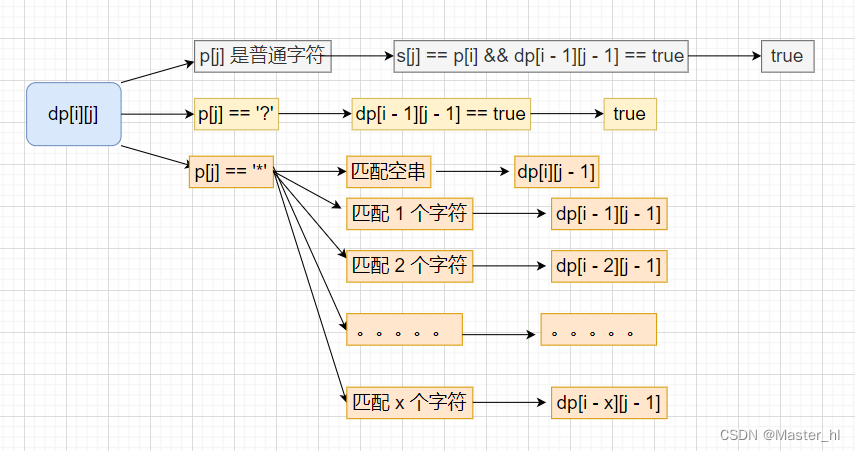
从上述分析来看，dp[i][j] 就得两层循环了，然后 * 的情况又需要遍历一遍，所以时间复杂度就上升到了 O（n^3），所以可以做一些优化，优化的思路如下：

优化的方向：看能不能将无穷个状态优化为一个或两个等有限个状态。

两种优化方法：

1. 数学
2. 根据状态表示以及实际情况优化状态转移方程

【方法一 】

 【方法二】

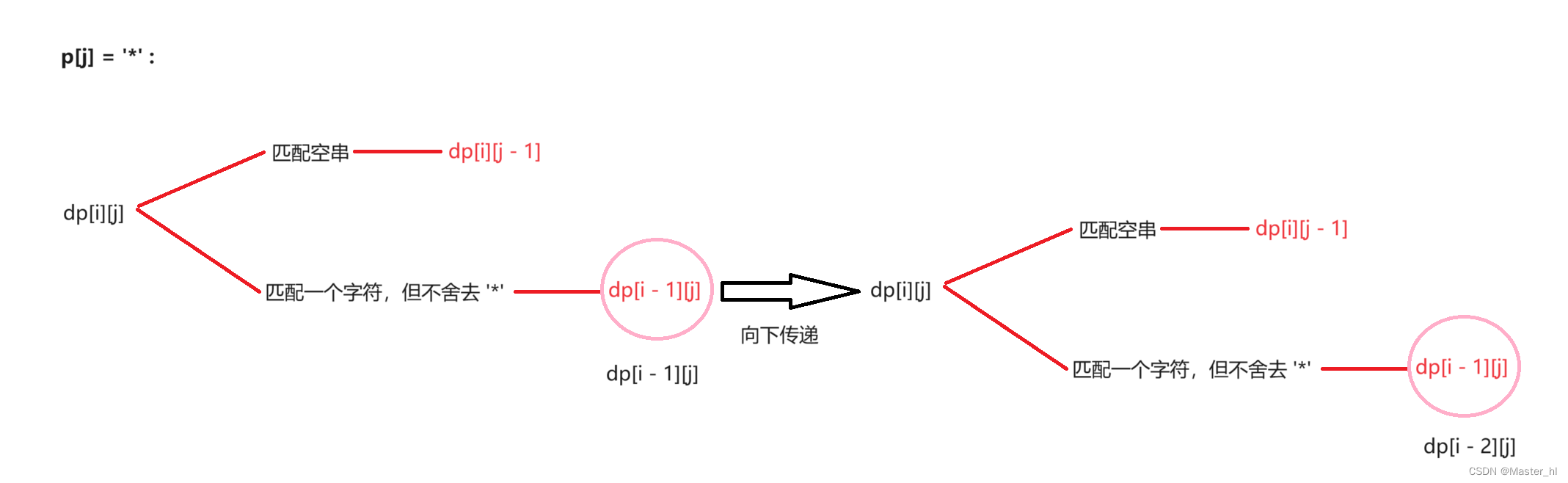
方法二是改变整体的状态转移方程，将原来的三种情况分为两种情况：

1. 匹配空串 
2. 匹配一个字符，但不舍去 '*' ，这种做法 ，也可以达到方法一的效果，因为 dp[i][j] 中的 '*' 传递给了 dp[i - 1][j]，dp[i - 1][j] 又可以传递给 dp[i - 2][j]，那么就相当于之前的穷举情况。

此时的状态转移方程依旧是 dp[i][j] = dp[i][j - 1] = dp[i - 1][j]。

2.3 编写代码

class Solution {
    public boolean isMatch(String ss, String pp) {
        int m = ss.length();
        int n = pp.length();
        ss = " " + ss; pp = " " + pp;
        char[] s = ss.toCharArray();
        char[] p = pp.toCharArray();
 
        boolean[][] dp = new boolean[m + 1][n + 1];
        //状态定义 dp[i][j] 表示：p[0,j] 区间内的子串能否匹配 s[0, i] 区间内的子串.
        // 初始化
        dp[0][0] = true;
        for(int j = 1; j <= n; ++j) {
            if(p[j] == '*') dp[0][j] = true;
            else break;
        }
        // 1. 普通字符 
        // 2. '?'
        // 3. '*'
        for(int i = 1; i <= m; ++i) {
            for(int j = 1; j <= n; ++j) {
                if(p[j] == '*') 
                    dp[i][j] = dp[i][j - 1] || dp[i - 1][j];
                else 
                    dp[i][j] = (p[j] == '?' || p[j] == s[i]) && dp[i - 1][j - 1];
            }
        }
        return dp[m][n];
    }
}

2.正则表达式匹配

2.1 题目描述

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
 
  '.' 匹配任意单个字符
  '*' 匹配零个或多个前面的那一个元素
所谓匹配，是要涵盖整个字符串 s 的，而不是部分字符串。

示例1：

输入：s = "aa", p = "a"
输出：false
解释："a" 无法匹配 "aa" 整个字符串。

示例2：

输入：s = "aa", p = "a*"
输出：true
解释：因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是
'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

 示例3：

输入：s = "ab", p = ".*"
输出：true
解释：".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。

2.2 算法原理

有了上题的基础之后，做这道题其实就稍微好做了一些。

状态定义：dp[i][j] 表示：p[0,j] 区间内的子串能否匹配 s[0, i] 区间内的子串. 【true or false】

【推导状态转移方程】

根据最后一个位置的状况，分情况讨论：

​​​​​​​

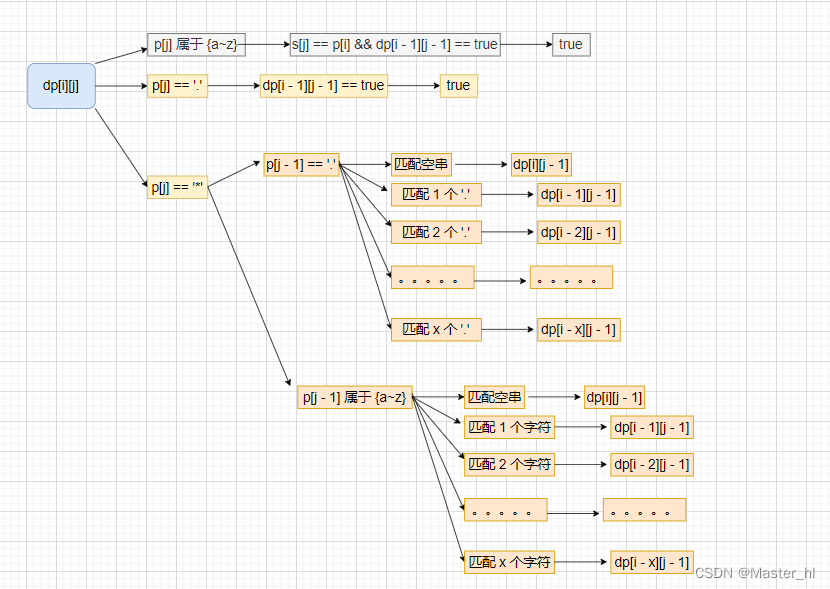
此处的状态转移方程，也可以使用前面的两种优化方式来降低时间复杂度。

最终的状态转移方程：

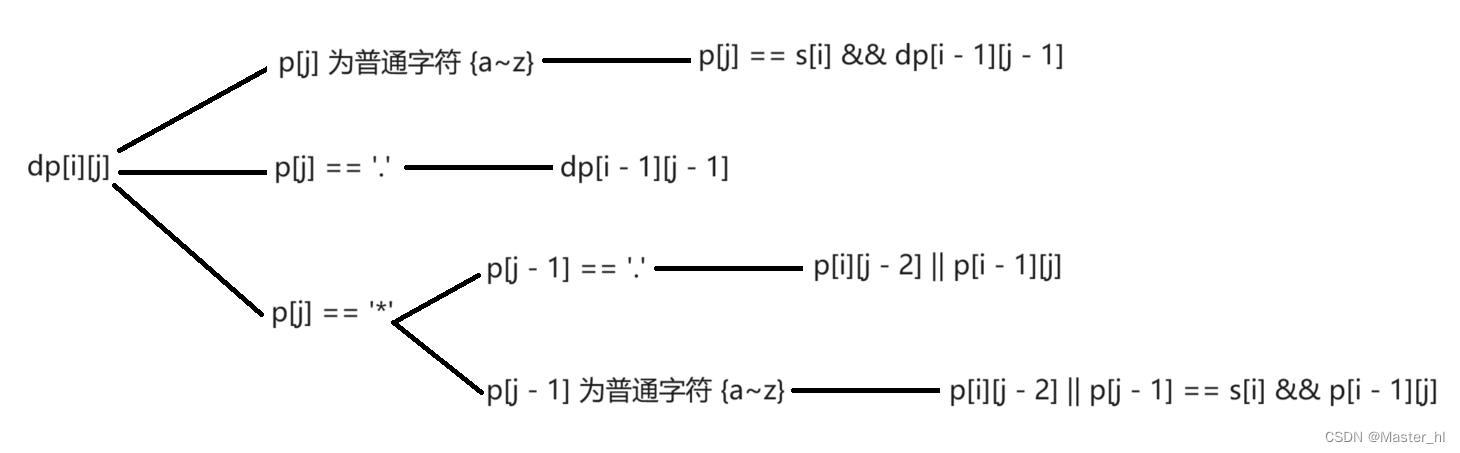
此处的第三种情况的两种小情况都可以参考通配符匹配的思路来理解。

2.3 编写代码

class Solution {
    public boolean isMatch(String ss, String pp) {
        int m = ss.length();
        int n = pp.length();
        ss = " " + ss; pp = " " + pp;
        char[] s = ss.toCharArray();
        char[] p = pp.toCharArray();
        boolean[][] dp = new boolean[m + 1][n + 1];
        // dp[i][j] 表示：pp 前 j 个字符能否匹配 ss 前 i 个字符
        // 初始化
        dp[0][0] = true;
        // 因为 '*' 必须搭配前面一个字符来用，所以偶数位置为 '*'，该位置就为 true
        for(int j = 2; j <= n; j += 2) {
            if(p[j] == '*') dp[0][j] = true;
            else break;
        }
        for(int i = 1; i <= m; ++i) {
            for(int j = 1; j <= n; ++j) {
                if(p[j] == '*') {
                    // 分两种大情况：前面是 '.' || 普通字符
                    if(p[j - 1] == '.')
                        // 分两种小情况：匹配空串 || 匹配 1~x 个'.'
                        dp[i][j] = dp[i][j - 2] || dp[i - 1][j];
                    else
                        // 分两种小情况：匹配空串 || 匹配 1~x 个普通字符
                        dp[i][j] = dp[i][j - 2] || p[j - 1] == s[i] && dp[i - 1][j];
                } else {
                    // 普通字符 || '.'
                    dp[i][j] = (p[j] == '.' || p[j] == s[i]) && dp[i - 1][j - 1];
                }
            }
        }
        return dp[m][n];
    }
}

3.扑克牌大小

3.1 题目描述

扑克牌游戏大家应该都比较熟悉了，一副牌由54张组成，含3~A，2各4张，小王1张，大王1张。
牌面从小到大用如下字符和字符串表示（其中，小写joker表示小王，大写JOKER表示大王）:)
3 4 5 6 7 8 9 10 J Q K A 2 joker JOKER
输入两手牌，两手牌之间用“-”连接，每手牌的每张牌以空格分隔，“-”两边没有空格，
如：4 4 4 4-joker JOKER
请比较两手牌大小，输出较大的牌，如果不存在比较关系则输出ERROR
 
基本规则：
（1）输入每手牌可能是个子，对子，顺子（连续5张），三个，炸弹（四个）和对王中的一种，
不存在其他情况，由输入保证两手牌都是合法的，顺子已经从小到大排列；
（2）除了炸弹和对王可以和所有牌比较之外，其他类型的牌只能跟相同类型的存在比较关系
（如，对子跟对子比较，三个跟三个比较），不考虑拆牌情况（如：将对子拆分成个子）
（3）大小规则跟大家平时了解的常见规则相同，个子，对子，三个比较牌面大小；
顺子比较最小牌大小；炸弹大于前面所有的牌，炸弹之间比较牌面大小；对王是最大的牌；
（4）输入的两手牌不会出现相等的情况。
 
答案提示：
（1）除了炸弹和对王之外，其他必须同类型比较。
（2）输入已经保证合法性，不用检查输入是否是合法的牌。
（3）输入的顺子已经经过从小到大排序，因此不用再排序了.
 
数据范围：保证输入合法

输入描述：

输入两手牌，两手牌之间用“-”连接，每手牌的每张牌以空格分隔，“-”两边没有空格，
如4 4 4 4-joker JOKER。

输出描述: 

输出两手牌中较大的那手，不含连接符，扑克牌顺序不变，仍以空格隔开；
如果不存在比较关系则输出ERROR。

3.2 题目分析

题目的重要信息:

1. 两个人的牌不能相同

2. 除了炸弹和王炸两种情况外, 两个人的牌必须可比较:

• 都是 个子(此处的个子不包括大小王)
• 都是 对子
• 都是 三个
• 都是 顺子(排好序的,且比较最小的那张牌),
• 都是 炸弹
• 一个人是 王炸, 另一个人拿什么都输
• 一个人是 炸弹,另一个人 非炸弹 (个子,对子,三个,顺子)

3.两副牌通过 '-' 分割, 牌之间通过 ' ' 分割.

3.3 代码实现

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        while (in.hasNextLine()) {
            String str = in.nextLine();
            // 存储两副牌(带空格), 用来输出
            String[] pp = str.split("-");
            // 存储两副牌(不带空格), 用来比较
            String[] p1 = pp[0].split(" ");
            String[] p2 = pp[1].split(" ");
            // 比较每副牌第一张牌的大小, 越靠后越大 (indexOf)
            String p = "34567891JDKA2";
            // 处理王炸的情况
            if(pp[0].equals("joker JOKER") || pp[1].equals("joker JOKER")) {
                System.out.println("joker JOKER");
            } else if(p1.length == p2.length) {
                // 处理类型相同的牌的情况
                if(p.indexOf(pp[0].substring(0,1)) > p.indexOf(pp[1].substring(0,1))) {
                    System.out.println(pp[0]);
                } else {
                    System.out.println(pp[1]);
                }
            } else if(p1.length == 4) {
                // 处理一方是炸弹的情况
                System.out.println(pp[0]);
            } else if(p2.length == 4) {
                System.out.println(pp[1]);
            } else {
                System.out.println("ERROR");
            }
        }
    }