状态压缩dp

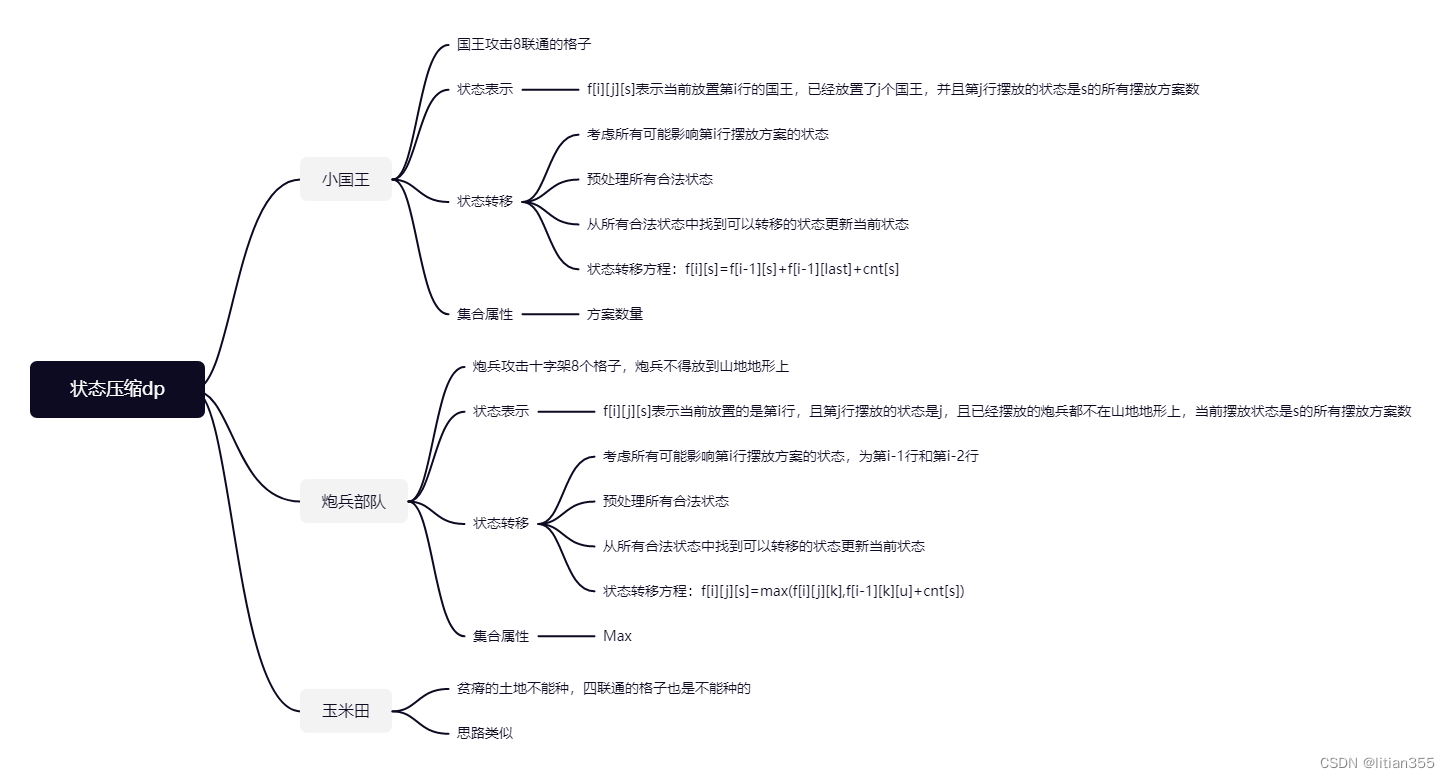
状态压缩dp就是，当你发现一个问题他在一个非常小的网格里摆放着稀奇古怪的玩意，它的数据范围非常小，你一眼dfs 的时候，突然发现答案过大，直接枚举会T，甚至需要取模，抑或是在一个相邻的区间最多能有几天可以进行k次操作，询问你答案，你却一筹莫展的时候，你想到了它。

但可以肯定的是，你有办法得到问题的答案。借助于二进制，借助于位运算，你把状态压缩成了二进制数，借助奇怪的位运算转移，然后你就成功了。

接下来让我们来看例题：

 

玉米田

农夫约翰的土地由 M×N个小方格组成，现在他要在土地里种植玉米。

非常遗憾，部分土地是不育的，无法种植。

而且，相邻的土地不能同时种植玉米，也就是说种植玉米的所有方格之间都不会有公共边缘。

现在给定土地的大小，请你求出共有多少种种植方法。

土地上什么都不种也算一种方法。

输入格式

第 1 行包含两个整数 M 和 N。

第 2..M+1 行：每行包含 N 个整数 0 或 1，用来描述整个土地的状况，1 表示该块土地肥沃，0 表示该块土地不育。

输出格式

输出总种植方法对 1e8 取模后的值。

数据范围

1≤M,N≤12

输入样例：

2 3
1 1 1
0 1 0

输出样例：

9

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=a;i<=b;i++)
const int N=14,M=1<<14;
int f[N][M];
int g[N][N];
vector<int >state[M],ok;
int cur[N];
int n,m;
 
bool check(int state){
	for(int j=0;j+1<=m;j++){
		if((state>>j&1)&&state>>(j+1)&1) return  false;
	}
	return true;
}
const int mod=1e8;
int main(){
	cin>>n>>m;
	//处理原数组cur表示当前
    rep(i,1,n) rep(j,0,m-1)
    {
		cin>>g[i][j];
		cur[i]|=!g[i][j]<<j;
	}
	for(int s=0;s<1<<m;s++){
	    if(check(s)) ok.push_back(s);
	}
   //预处理所有合法状态可能到达的状态
	for(int i=0;i<ok.size();i++){
		for(int j=0;j<ok.size();j++){
			int sa=ok[i],sb=ok[j];
			if(sa&sb) continue;
			state[i].push_back(sb);
		}
	}
	f[0][0]=1;//当前摆的是0-th floor 且状态是0的方案数是0
	for(int i=1;i<=n+1;i++){//迭代n+1次答案就是f[n+1][0];
		for(int j=0;j<ok.size();j++){//枚举当前这一行的所有可能状态
		    if(ok[j]&cur[i]) continue;//排除因为贫瘠土地不合法的状态
		    for(int k=0;k<state[j].size();k++){//枚举当前这一行所有可能到达的状态
				int a=ok[j],b=state[j][k];
				if(a&b) continue;
				f[i][a]=(f[i][a]+f[i-1][b]) %mod;
			}	
			
			
		}
	}
	cout<<f[n+1][0]<<endl;
	return 0;
}

2.小国王，因为思路都是类似的，就只在代码里面加注释了

对于状态压缩dp问题，我们不仅需要考虑转移前的状态是否是合法的还需要考虑转移后的状态是否合法。

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define rep(i,a,b) for(int i=a;i<=b;i++)
const int N=12,M=1<<12,K=110;
int n,m;
 
int f[N][K][M];//f[i][j][s]表示当前填的是第i行已经填了j个国王，且状态是s的方案数
int cnt[M];//记录在一行中可能出现所有方案中国王的个数
vector<int >ok,state[M];
bool check(int s){
	for(int i=0;i<n;i++){
	   if((s>>i&1)&&(s>>(i+1)&1)) return false;
	}
	return true;
}
int count(int s){//计算国王个数
	int res=0;
	for(int i=0;i<n;i++){
	  if(s>>i&1) res++;
	}
	return res;
}
signed  main(){
    cin>>n>>m;
    for(int s=0;s<1<<n;s++){
	  if(check(s)) ok.push_back(s);	
	  cnt[s]=count(s);
	}
    for(int i=0;i<(int)ok.size();i++){
		for(int j=0;j<(int )ok.size();j++){
			int sa=ok[i],sb=ok[j];
		   if((sa&sb)==0&&check(sa|sb)) state[i].push_back(j);//sa|sb 也必须是合法状态！！
		}
	}
	f[0][0][0]=1;
	for(int i=1;i<=n+1;i++){
	   for(int j=0;j<=m;j++){
	   	for(int a=0;a<(int)ok.size();a++){
		for(int b:state[a]){
	       int c=cnt[ok[a]];
	       if(j>=c) f[i][j][a]+=f[i-1][j-c][b];
		}
	   }
	}
	}
	
		cout<<f[n+1][m][0]<<endl;
	return 0;
}

292. 炮兵阵地​​​​​​​​​​​​

司令部的将军们打算在 N×M 的网格地图上部署他们的炮兵部队。

一个 N×M 的地图由 N行 M 列组成，地图的每一格可能是山地（用 H 表示），也可能是平原（用 P 表示），如下图。

在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。

图上其它白色网格均攻击不到。

从图上可见炮兵的攻击范围不受地形的影响。

现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

输入格式

第一行包含两个由空格分割开的正整数，分别表示 N 和 M；

接下来的 N 行，每一行含有连续的 M 个字符(P 或者 H)，中间没有空格。按顺序表示地图中每一行的数据。

输出格式

仅一行，包含一个整数 K，表示最多能摆放的炮兵部队的数量。

数据范围

N≤100,M≤10

输入样例：

5 4
PHPP
PPHH
PPPP
PHPP
PHHP

输出样例：

6

 思路：规定好从第一行开始向下摆放那么能够影响当前这一行炮兵摆放的就只有它的上一行和上上一行，我们先预处理出对于一行而言所有合法摆放方案，同时开一个新的数组记录这个状态可以摆多少个炮兵，方便后续转移，再据此找出所有以某一状态为终点的所有可能转移方式，开始dp就行了，注意：因为数据范围比较大，会爆空间，所以我们可以用滚动数组优化，滚动数组会降低空间复杂度，但不会降低时间复杂度。

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=a;i<=b;i++)
const int N=102,M=11,S=1<<M;
int  n,m;
int cur[N];
int cnt[S];
vector<int >ok,state[S];
char g[N][M]; 
 
bool check(int s){
	for(int i=0;i<m;i++){
		if((s>>i&1)&&((s>>i+1&1)||s>>(i+2)&1)) return false;
	}
	return true;
}
int count(int s){
	int res=0;
	while(s)
    {
		res+=s&1;
		s>>=1;
	}
	return res;
}
int f[2][S][S];//滚动数组优化空间
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++) {
		cin>>g[i];
	}
	for(int i=1;i<=n;i++)
	{
	  for(int j=0;j<m;j++){
	  	if(g[i][j]=='H') cur[i]|=1<<j;
	  }
	}
	for(int s=0;s<1<<m;s++){
		if(check(s)) ok.push_back(s),cnt[s]=count(s);
	}
	int sz=ok.size();
  // cout<<ok.size()<<endl;
	for(int i=1;i<=n+2;i++)//迭代到n+2
	{
		for(int j=0;j<sz;j++){
		  for(int k=0;k<sz;k++){
		  	for(int u=0;u<sz;u++){
			  	int a=ok[j],b=ok[k],c=ok[u];
			  	if((a&b)||(a&c)||(b&c)) continue;如果不能相互转移
			  	if(cur[i]&b||cur[i-1]&a||cur[i-2]&c) continue;//如果有高原
			  	f[i&1][j][k]=max(f[i&1][j][k],f[i-1&1][u][j]+cnt[b]);
			  }
		  }
		}
	}
	cout<<f[n+2&1][0][0]<<endl;//答案就是已经摆放了n行且当前摆放状态是0，上一行也是0
	return 0;
}
 
//5 4
//PHPP
//PPHH
//PPPP
//PHPP
//PHHP
//6