- 1学习Java, 发现switch竟有三种用法方式! 速学!_java switch 直通式
- 2python如何做到只在服务启动时执行_在后台启动时执行python脚本
- 3职级P1到P12等级体系详解_吉利p1到p12的岗位级别
- 4ESP8266驱动五线四相步进电机_esp8266控制步进电机
- 5备战蓝桥杯---搜索(剪枝)
- 6叮咚~请查收你的2023年度AI项目实战报告
- 7windows搜索根据关键字查找不到文件-通配符使用_windows根据关键字复制文件
- 8kafka单节点部署,亲测可行!_kafka一个节点可以吗
- 9MVC模式和MVP模式的区别_mvc mvp 区别
- 10基于视频的移动目标检测 Moving Object Detection_moving object detection and tracking from video ca
AES加密算法代码实现
赞
踩
AES加密算法代码实现
作业目标
C语言实现AES加密算法,并将其优化到尽量快的速度。
算法描述
AES简介
高级加密标准(AES,Advanced Encryption Standard)为最常见的对称加密算法,又称Rijndael加密法,是美国联邦政府采用的一种区块加密标准。
对称加密算法:加密和解密用相同的密钥。加密密钥能够从解密密钥中推算出来,同时解密密钥也可以从加密密钥中推算出来。
对称加密算法的特点是算法公开、计算量小、加密速度快、加密效率高。
- 整体流程
在对称加密算法中,数据发信方将明文(原始数据)和加密密钥(mi yao)一起经过特殊加密算法处理后,使其变成复杂的加密密文发送出去。收信方收到密文后,若想解读原文,则需要使用加密用过的密钥及相同算法的逆算法对密文进行解密,才能使其恢复成可读明文。如下图所示:
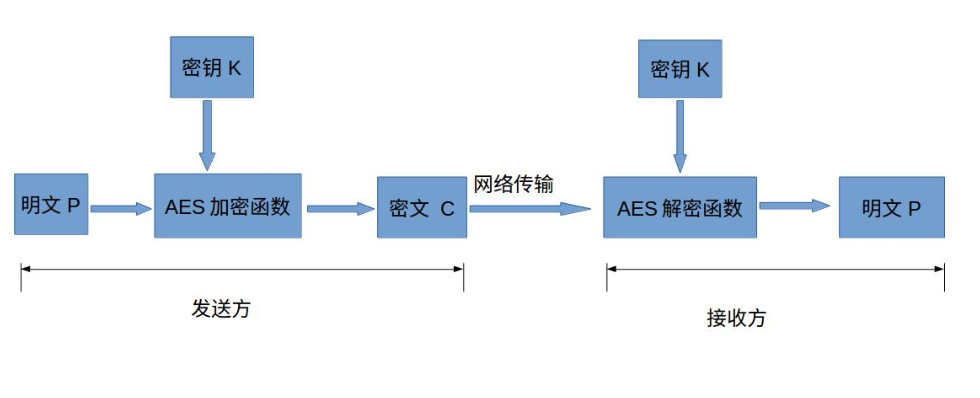
- 加密流程
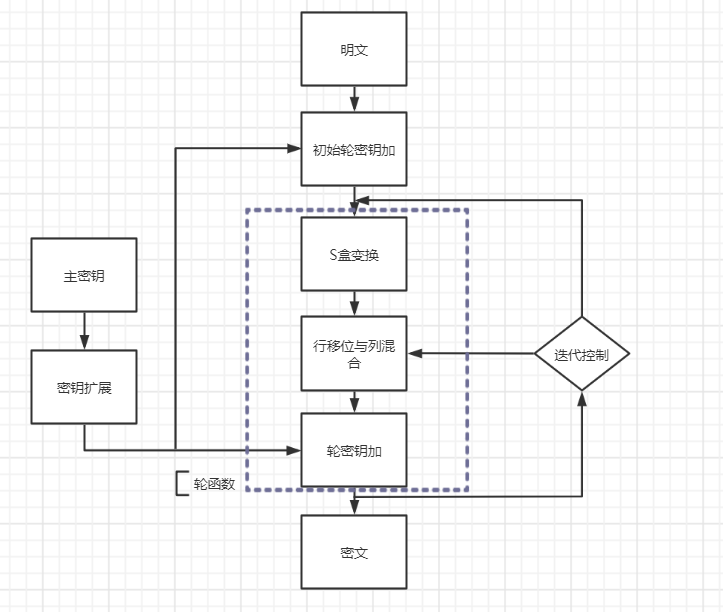
图中轮函数由三层组成:- 第一层是S盒变换 ByteSub,是非线性的字符变换,有__混淆__作用
- 第二层是行移位变换ShiftRow + 列混合变换MixColumn,确保多轮之上的高度__扩散__
- 第三层是轮密钥加变换AddRoundKey,将轮密钥简单地异或到中间状态上,实现密钥的__加密控制__作用
注意:可以看到最后一次变换,指向第二层,实际上并不进行列混合
- 解密流程
与加密类似,如下图:
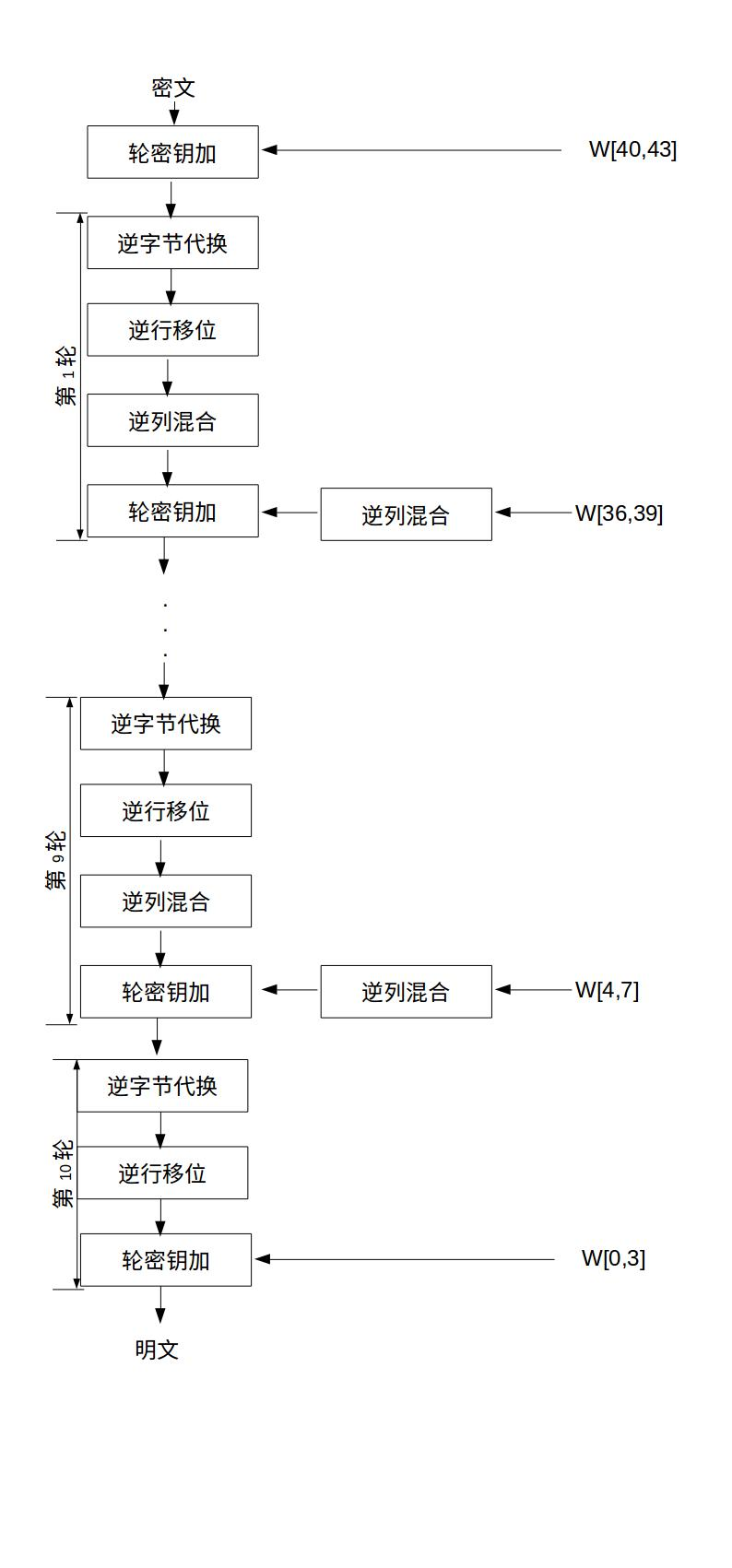
实验设计
- 所需常量:
- 数组定义S盒以及S盒逆
- 轮常数,防止不同轮的轮密钥存在相似性
- 列混合(加密);逆列混合(解密)
- 所需函数
- 字节替代SubBytes
- 逆字节替代InvSubBytes
- 行移位和逆行移位ShiftRows
- 列混合MixColumns
- 逆列混合InvMixColumns
- 密钥加AddRoundKey
- 密钥扩展KeyExpansion
- 获取轮密钥GetRoundKey
- 加密函数Encrypt(调用字节替代、行移位、列混合、密钥加、密钥扩展、获取轮密钥)
- 解密函数Decrypt(调用逆字节替代、逆行移位、逆列混合、密钥加、密钥扩展、获取轮密钥)
- 主函数main
- 调用 x( ):控制流程,方便递归使用
S盒 与 S盒逆
用数列定义:
int s_box[256] = { 0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76, 0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0, 0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15, 0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75, 0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84, 0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF, 0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8, 0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2, 0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73, 0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB, 0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79, 0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08, 0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A, 0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E, 0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF, 0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
int Invers_box[256] = { 0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5, 0x38, 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB, 0x7C, 0xE3, 0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, 0x34, 0x8E, 0x43, 0x44, 0xC4, 0xDE, 0xE9, 0xCB, 0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D, 0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E, 0x08, 0x2E, 0xA1, 0x66, 0x28, 0xD9, 0x24, 0xB2, 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B, 0xD1, 0x25, 0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xD4, 0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92, 0x6C, 0x70, 0x48, 0x50, 0xFD, 0xED, 0xB9, 0xDA, 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D, 0x84, 0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, 0xF7, 0xE4, 0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06, 0xD0, 0x2C, 0x1E, 0x8F, 0xCA, 0x3F, 0x0F, 0x02, 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B, 0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, 0x97, 0xF2, 0xCF, 0xCE, 0xF0, 0xB4, 0xE6, 0x73, 0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD, 0x35, 0x85, 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E, 0x47, 0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, 0x6F, 0xB7, 0x62, 0x0E, 0xAA, 0x18, 0xBE, 0x1B, 0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79, 0x20, 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4, 0x1F, 0xDD, 0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, 0xB1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xEC, 0x5F, 0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D, 0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF, 0xA0, 0xE0, 0x3B, 0x4D, 0xAE, 0x2A, 0xF5, 0xB0, 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53, 0x99, 0x61, 0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, 0xE1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
字节替换与逆字节替换
void SubBytes(int a[4][4],int s_box[256])
{
int i,j;
for (i = 0; i < 4; i++){
for (j = 0; j < 4; j++){
a[i][j] =s_box[a[i][j]];
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
可以看到,a数组是我们输入的要加密的明文,把a中每一位上的数字对应换成S盒中的数字,即完成转换。
void InvSubBytes(int a[4][4],int InverS_box[256])/* InverS_box[256]是逆S盒*/
{
int i,j;
for (i = 0; i < 4; i++)
for (j = 0; j < 4; j++)
a[i][j] = InverS_box [a[i][j]];
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
行移位和逆行移位
void ShiftRows(int a[4][4],int decrypt)
- 1
使用变量decrypt,加密时decrypt = 0,进行行移位;解密时decrypt = 1,进行逆行移位。
实现加密行移位功能
if(decrypt==0){ /* 此时实现加密行移位功能 */ for(i=1;i<4;i++) { if(i==1){ j=a[i][0]; a[i][0]=a[i][1]; a[i][1]=a[i][2]; a[i][2]=a[i][3]; a[i][3]=j;} if(i==2){ j=a[i][0]; b=a[i][1]; a[i][0]=a[i][2]; a[i][1]=a[i][3]; a[i][2]=j; a[i][3]=b;} if(i==3){ j= a[i][3]; a[i][3]=a[i][2]; a[i][2]=a[i][1]; a[i][1]=a[i][0]; a[i][0]=j;} } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
很容易看出来,就是第一行不动,把第2,3,4行每一列对应的数右移1,2,3位。如下图所示:
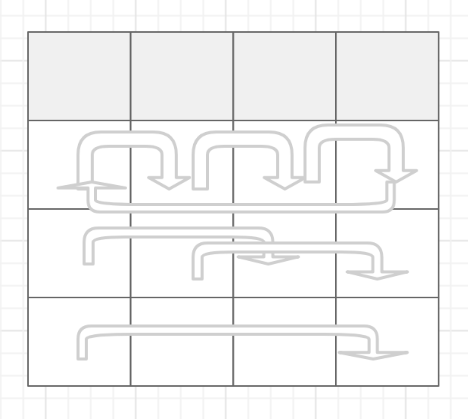
解密逆行移位功能
if(decrypt==1) { /* 此时实现解密逆行移位功能 */ for(i=1;i<4;i++) { if(i==1){ j=a[i][3]; a[i][3]=a[i][2]; a[i][2]=a[i][1]; a[i][1]=a[i][0]; a[i][0]=j;} if(i==2){ j=a[i][0]; b=a[i][1]; a[i][0]=a[i][2]; a[i][1]=a[i][3]; a[i][2]=j; a[i][3]=b;} if(i==3){ j=a[i][0]; a[i][0]=a[i][1]; a[i][1]=a[i][2]; a[i][2]=a[i][3]; a[i][3]=j;} } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
解密的行移位就是逆同理再转回去
列混合与列逆混合
在AES算法中,需要模多项式m(x)=x8+x4+x^3+x+1。列混合即是用一个常矩阵乘以第二步变换后的矩阵,以达到矩阵中每一个元素都是该元素原所在列所有元素的加权和。如下图所示:
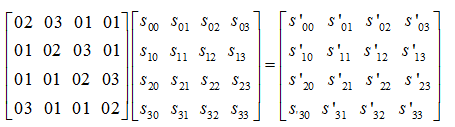
c(x) = 0x03*x^3 + 0x01*x^2 + 0x01*x + 0x02
01=1
02 = x
03 = x + 1
b[4][4]为列混合时的固定矩阵
int b[4][4]={0x02,0x03,0x01,0x01,
0x01,0x02,0x03,0x01,
0x01,0x01,0x02,0x03,
0x03,0x01,0x01,0x02};
- 1
- 2
- 3
- 4
列混合具体函数
void MixColumns(int a[4][4],int b[4][4]) /*b[4][4]为列混合时的固定矩阵*/ { int temp[4][4]={0}; int d[3]={0x80,0x1B,0x02}; int i,j,m,k; for(m=0;m<4;m++){ for (i = 0; i<4;i++){ for (j = 0;j<4;j++){ if(b[i][j]==1) temp[i][m]=a[j][m]^temp[i][m]; else { if(b[i][j]==2){ if(a[j][m]<d[0]){ temp[i][m]=(b[i][j]*a[j][m])^temp[i][m]; } else{ k=a[j][m]^d[0]; temp[i][m]=((b[i][j]*k)^d[1])^temp[i][m]; } } else{ if(a[j][m]<d[0]) temp[i][m]=((a[j][m]*d[2])^a[j][m])^temp[i][m]; else{ k=a[j][m]^d[0]; temp[i][m]=(((k*d[2])^d[1])^a[j][m])^temp[i][m]; } } } } } } for(i=0;i<4;i++) for(j=0;j<4;j++) a[i][j]=temp[i][j]; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
利用矩阵乘法,对应位置相乘,再相加,注意相加是异或操作。
先要声明一个空白的temp矩阵,在计算中临时存储每一步的结果,并将最终结果导入a中其中
int d[3]={0x80,0x1B,0x02}是一个用来实现x乘法的数组,用来判断处理溢出和进位
解密时逆向列混合同理:
列逆矩阵
int c[4][4]={0x0E,0x0B,0x0D,0x09,
0x09,0x0E,0x0B,0x0D,
0x0D,0x09,0x0E,0x0B,
0x0B,0x0D,0x09,0x0E};
- 1
- 2
- 3
- 4
列逆混合函数
void InvMixColumns(int a[4][4],int c[4][4]) /*c[4][4]为逆列混合时的固定矩阵*/ { int temp[4][4]={0}; int d[7]={0x80,0x1B,0x02,0x0e,0x0b,0x0d,0x09}; int i,j,m,n,e,k,p,q,x,y; for(m = 0;m < 4;m++) for (i = 0; i < 4;i++) for (j = 0;j < 4;j++){ e=a[j][m];y=a[j][m]; if(c[i][j]==d[3]){ for(n=0;n<3;n++){ if(y<d[0]) y=y*d[2]; else{ k=y^d[0]; y=(k*d[2])^d[1];} if(n==0) {p=y;} else if(n==1) {q=y;} else { x=y;} } temp[i][m]=p^q^x^temp[i][m];} if(c[i][j]==d[4]) {for(n=0;n<3;n++) { if(y<d[0]) y=y*d[2]; else {k=y^d[0]; y=(k*d[2])^d[1];} if(n==0) q=y; if(n==2) x=y;} temp[i][m]=e^q^x^temp[i][m];} if(c[i][j]==d[5]) {for(n=0;n<3;n++) { if(y<d[0]) y=y*d[2]; else {k=y^d[0]; y=(k*d[2])^d[1];} if(n==1) q=y; if(n==2) x=y;} temp[i][m]=e^q^x^temp[i][m];} if(c[i][j]==d[6]){ for(n=0;n<3;n++){ if(y<d[0]) y=y*d[2]; else{ k=y^d[0]; y=(k*d[2])^d[1];} } temp[i][m]=e^y^temp[i][m]; } } for(i=0;i<4;i++) for(j=0;j<4;j++) a[i][j]=temp[i][j]; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
密钥扩展
void KeyExpansion(int roundkey[4][4],int s_box[256], int temp[4][44]) { int i,j,n,m,a,b,x,y; int w[4],r[4],q[4]; for(i=0;i<4;i++) for(j=0;j<4;j++) {temp[i][j]= roundkey[i][j];} for(i=4;i<44;i++){ a=i-4;b=i-1; if(i%4!=0){/*i不是4的倍数*/ for(j=0;j<4;j++) q[j]=temp[j][a]^temp[j][b]; for(y=0;y<4;y++) temp[y][i]=q[y]; } else{ /*i是4的倍数*/ for(x=0;x<4;x++) w[x]=temp[x][b]; n=w[0]; /*左移一位*/ w[0]= w[1]; w[1]= w[2]; w[2]= w[3]; w[3]=n; for(j=0;j<4;j++) w[j]=s_box[w[j]];/*字节替代*/ w[0]= rcon[(i-4)/4]^w[0]; for(m=0;m<4;m++) r[m]=temp[m][a]^w[m]; for(y=0;y<4;y++) temp[y][i]=r[y]; } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
AES首先将初始密钥输入到一个44的状态矩阵中,这个44矩阵的每一列的4个字节组成一个字,矩阵4列的4个字依次命名为W[0]、W[1]、W[2]和W[3],它们构成一个以字为单位的数组W。
接着,对W数组扩充40个新列,构成总共44列的扩展密钥数组。新列以如下的规则产生:
- 如果i不是4的倍数,那么第i列由如下等式确定:
W[i]=W[i-4]⨁W[i-1] - 如果i是4的倍数,那么第i列由如下等式确定:
W[i]=W[i-4]⨁T(W[i-1])
其中,T是一个有点复杂的函数。
函数T由3部分组成:字循环、字节代换和轮常量异或,这3部分的作用分别如下。- a.字循环:将1个字中的4个字节循环左移1个字节。即将输入字[b0, b1, b2, b3]变换成[b1,b2,b3,b0]。
- b.字节代换:对字循环的结果使用S盒进行字节代换。
- c.轮常量异或:将前两步的结果同轮常量Rcon[j]进行异或,其中j表示轮数。
伦常量如下:
/*轮常数,防止不同轮的轮密钥存在相似性*/ const int rcon[10]={0x01,0x02,0x04, 0x08,0x10,0x20,0x40, 0x80,0x1B,0x36};- 1
- 2
- 3
- 4
获取轮密钥
/*获取轮密钥*/
void GetRoundKey(int roundKey[4][4], int temp[4][44],int n)
{
int i,j;
for(i=0;i<4;i++)
for(j=0;j<4;j++)
roundKey[i][j]=temp[i][j+4*n];
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
密钥加
void AddRoundKey(int a[4][4],int roundKey[4][4])
{
int i,j;
for (i = 0;i < 4; i++)
for (j = 0; j < 4; j++)
a[i][j] = a[i][j] ^ roundKey[i][j];
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
轮密钥加是将128位轮密钥Ki同状态矩阵中的数据进行逐位异或操作
注意:轮密钥加的逆运算同正向的轮密钥加运算完全一致,这是因为异或的逆操作是其自身。轮密钥加非常简单,但却能够影响S数组中的每一位。
加密函数
void Encrypt(int a[4][4],int roundKey[4][4],int temp[4][44]) { int i,j,n; int decrypt = 0; AddRoundKey(a,roundKey);/* 轮密钥加*/ for(n=1;n<=10;n++) { if(n==10){ SubBytes(a,s_box); /* 字节替代*/ ShiftRows(a,decrypt); /*行移位*/ GetRoundKey(roundKey,temp,n); /* 获取轮密钥*/ AddRoundKey(a,roundKey); /* 轮密钥加*/ } else{ SubBytes(a,s_box); /* 字节替代*/ ShiftRows(a,decrypt); /*行移位*/ MixColumns(a,b); /* 列混合*/ GetRoundKey(roundKey,temp,n); /* 获取轮密钥*/ AddRoundKey(a,roundKey); /* 轮密钥加*/ } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
去掉显示的提示信息可以发线,就是之前画好的流程图,并且区别开最后一轮没有列混合
注意:decrypt = 0表示加密
解密函数
与加密函数类似
void Decrypt(int a[4][4],int roundKey[4][4],int temp[4][44]) { int i,j,n,m; int decrypt = 1; int r[10]={0,9,8,7,6,5,4,3,2,1}; m=10; GetRoundKey(roundKey, temp,m); AddRoundKey(a,roundKey); for(n=1;n<=10;n++) { if(n==10) { ShiftRows(a,decrypt); InvSubBytes(a,Invers_box); m=0; GetRoundKey(roundKey,temp,m); AddRoundKey(a,roundKey); } else{ ShiftRows(a,decrypt); InvSubBytes(a,Invers_box); m=r[n]; GetRoundKey(roundKey, temp,m); AddRoundKey(a,roundKey); InvMixColumns(a,c); } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
注意获取轮密钥时需要对应反序
m = 10 -n,每次都运算应该是没有建立数组查表快的。
流程函数x()
-
控制流程,方便递归使用
-
输入明文和初始密钥,进行最初的加密
-
输入初始密钥(注:需输入32个字符,且每个字符必须在0-a之间,否则出错),转化为16进制矩阵
scanf("%s",k); for(j=0;j<32;j++) { if(k[j]!='\0'&&k[j]<='f') if(k[j]<'a') l[j]=k[j]-'0'; else l[j]=10+(k[j]-'a'); else { printf(" 输入出错\n"); x(); }} for(n=0;n<32;n=n+2){ m=n/2; l[m]=l[n]*16+l[n+1]; } for(i=0;i<4;i++) for(j=0;j<4;j++) key[j][i]=l[j+i*4];
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
需要扩展加密
KeyExpansion(key,s_box,Temp); Decrypt(w,key,Temp); x();- 1
- 2
- 3
- 输入明文块(注:需输入32个字符,且每个字符必须在0-a之间,否则出错,检查类似)
for(i=0;i<32;i++) p[i]='0'; scanf("%s",o);//char o[32] for(i=0;o[i]!='\0';i++) p[i]=o[i]; for(i=0;i<32;i++){ if(p[i]!='\0'&&p[i]<='f') if(p[i]<'a') s[i]=p[i]-'0'; else s[i]=10+(p[i]-'a'); else{ printf(" 输入出错\n"); x(); } for(n=0;n<32;n=n+2){ m=n/2; s[m]=s[n]*16+s[n+1];//int s[32] } for(i=0;i<4;i++) for(j=0;j<4;j++) w[j][i]=s[j+i*4];
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
将输入的字符(0-10的字符串例如’123a’)一个一个到处转化为数字(例如’1’‘2’‘3’‘10’),再将两位拼成16进制数(例如’0x12(16+2)’‘0x3a(3*16+10)’),最后将int s[16]按列放入int w[4][4]。
-
优化技巧
打破输入限制,加入时间计算
原先是输入32个字符,且每个字符必须在0-a之间,否则出错,我们直接把它们都删掉,写一个导入加密文件的函数,再将文件内容转化为ascii码,将内容切片成需要的大小128位()
if (fp != NULL) { while ((ch = fgetc(fp)) != EOF){ s[num % 16] = (uint8_t)ch; for(i=0;i<4;i++) for(j=0;j<4;j++) w[j][i]=(int)s[j+i*4]; if (num != 0 && num % 16 == 0) { ftime(&ts1); KeyExpansion(key,s_box,Temp); Encrypt(w,key,Temp); ftime(&ts2); t_sec = ts2.time - ts1.time; t_ms = ts2.millitm - ts1.millitm; ti += t_sec * 1000 + t_ms; } num++; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
目前只完成了加密部分的改写
S盒查表
使用查表法能大幅提升加密速度
int s_box[256] = [...]
- 1
列混合优化
使用固定矩阵乘法更方便
int b[4][4]={0x02,0x03,0x01,0x01,
0x01,0x02,0x03,0x01,
0x01,0x01,0x02,0x03,
0x03,0x01,0x01,0x02};
- 1
- 2
- 3
- 4
没有实现列混合查表,放一个目标参考(表如下:)
参考:https://gitee.com/lee_ka/AES/blob/master/1gai.cpp
unsigned char L_box(int i,unsigned char j) { return L_boxx[i][j]; } static void MixColumns(unsigned char *col)//列混合 { unsigned char tmp[4],xt[4]; int i; for(i=0;i<4;i++,col+=4) //col代表一列的基地址,col+4:下一列的基地址 { tmp[0]=L_box(1,col[0])^L_box(2,col[1])^col[2]^col[3]; tmp[1]=col[0]^L_box(1,col[1])^L_box(2,col[2])^col[3]; tmp[2]=col[0]^col[1]^L_box(1,col[2])^L_box(2,col[3]); tmp[3]=L_box(2,col[0])^col[1]^col[2]^L_box(1,col[3]); //修改后的值 直接在原矩阵上修改 col[0]=tmp[0]; col[1]=tmp[1]; col[2]=tmp[2]; col[3]=tmp[3]; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
转置输入
AES的数据是按列输入的,而这样在计算机中操作并不方便,将AES转置后可以按行输入数据,这样可以使用指针的强制类型转换来减少循环的轮次,注意在转置后的部分操作也要进行转置的变化,包括行移位和列混淆(见行移位和列混淆代码),AES的转置实现见-AES转置实现。注意在对指针进行强行转换后会出现int内部的字节倒序的现象。
for(i=0;i<4;i++)
for(j=0;j<4;j++)
w[j][i]=(int)s[j+i*4];
- 1
- 2
- 3
函数表达更清晰(还没有改)
unsigned char xtime(unsigned char st) { return (st<<1)^((st&0x80)?0x1b:0x00); //x乘法 二进制串左移一位,判断最高位是否溢出,溢出要异或0x1b } void mixcolumns(unsigned char state[4][4],unsigned char cipher[4][4]) { for(int j=0;j<4;j++) { for(int i=0;i<4;i++) { cipher[i][j]= xtime(state[i%4][j]) //0x02乘法 ^(state[(i+1)%4][j])^xtime(state[(i+1)%4][j])//0x03乘法 ^state[(i+2)%4][j] //0x01乘法 ^state[(i+3)%4][j]; //0x01乘法 } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
实验结果与反思
实验结果
2963 ms v = 3538.89976 Byte/ms

总结
本次实验实现了AES对文本的加密,更加深入地学习了AES算法的使用流程以及加密过程,在列混淆以及加密密钥环节遇到了诸多困难,对于矩阵乘法和异或操作有了更深入的认识,由此也想到了很多优化的方法。由于时间的限制优化并没有完全完成:没有实现列混合查表;列混淆那里的矩阵乘法代码看上去有些混乱,可能可以加一个函数调用会更易读;没有保存加密好的新文件并对其解密。
完整代码
见压缩包
备注:aes_1:有解密,但是输入限制。
aes_2:用于测试,可以加密文件。
- 进行上述链接的相关操作后,重新开机(sudoreboot)后,进入了terminal界面,但是需要重新输入用户密码,同时condaactivateyolov5语句报错,无法进入conda环境。例如博主本人需要(1)给NX版的串口赋值使能权限... [详细]
赞
踩
- 每个SpringBoot版本和内置容器不同,结果也不同,这里以SpringBoot2.7.10版本+内置Tomcat容器举例。_springboot自带tomcat的最大连接数和最大并发数springboot自带tomcat的最大连接数和最... [详细]
赞
踩
- 两台PMAC之间使用ModbusTcp做主从通讯服务端配置客户端配置连接服务端读取线圈写线圈读浮点数写浮点数服务端配置服务端IP:192.168.0.201在globaldefinitions.pmh文件开启Modbus服务,并设置几个用于... [详细]
赞
踩
- 如何在Ubuntu18.04.2LTS系统环境下运行,双击一个文件(快捷方式),运行一个程序,或者打开一个软件呢?1,首先,打开gedit软件,编写程序,如:gedit或者nautilus保存为test.sh文件。2选中文件,然后在屏幕左上... [详细]
赞
踩
- 一个ip发请求过来,是一个ip对应一个线程吗?我突然愣住了,对于SpringBoot如何处理请求好像从来没仔细思考过,所以面试结束后就仔细研究了一番,现在就来探讨一下这个问题。_springboot并发数量限制springboot并发数量限... [详细]
赞
踩
- 本节讲解了双向链表的结构,以及实现了一个双向链表及功能,不得不说双向链表比单链表写起来简单多了,没有那么多繁琐的条件判断数据结构·双向链表1.双向链表的结构 我们之前提到过,双向链表的全称是:带... [详细]
赞
踩
- 这篇文章是基于“一个SpringBoot项目能同时处理多少请求?”这个面试题出发的。但是经过我们前面简单的分析,你也知道,这个问题如果在没有加一些特定的前提条件的情况下,答案是各不一样的。比如我再给你举一个例子,还是我们的Demo,只是使用... [详细]
赞
踩
- 与官方文档和同类书不同的是,本书对OpenCV函数进行了大量测试,着重讲解函数中参数的格式要求和注意事项,并结合例程帮助读者理解每个函数的特殊规定。但是,我在查阅的十几种数字图像处理教材和关于OpenCV的图书时发现,它们似乎分属两个门派,... [详细]
赞
踩
- Python操作Word、Excel、PPT、PDF\、复杂文件、通信软件(微信、邮件、飞书、钉钉)、图片目录 章节一:python使用openpyxl操作excel 1、openpyxl库介绍 2、python怎么打开及读取... [详细]
赞
踩
- C++的类赋值运算符重构_c++类的赋值重写c++类的赋值重写创作内容不易,学习的朋友麻烦关注下博主,后面学习不迷路。有不会的问题也可以论坛咨询博主,博主也会及时回复~~将已有的对象赋给另一个对象时,将使用重载的赋值运算符而复制构造函数和赋... [详细]
赞
踩
- Alpaca是Stanford用52k指令数据微调LLaMA7B后得到的预训练模型,作者声称在单轮指令执行的效果上,Alpaca的回复质量和openai的text-davinci-003相当,但是Alpaca的参数非常少(微调一个7B的ll... [详细]
赞
踩
- 总的解决思路编写xxx.service文件导入到/etc/systemd/system,最终通过systemctlstartxxx.service启动服务,通过systemctlenablexxx.service实现开机自启动。如何编写自己... [详细]
赞
踩
- 土堆视频文章目录前言Jupyter的使用ESC命令模式双击编辑模式dir和help使用[Pytorch中TensorVariableParameter以及求导运算](https://blog.csdn.net/qq_42283621/art... [详细]
赞
踩
- 写一个GF(2^8)下可做任意两个数乘法的程序。在GF(2^8)中只有两种运算:(1)加法,即异或运算(2)乘法,乘2时即左移一位,溢出时异或1BH_有限域gf(2^8)上乘法有限域gf(2^8)上乘法作业要求:写一个GF(2^8)下可做任... [详细]
赞
踩
- 通用大模型虽好,但通过微调得到一个专属大模型不仅可以提高模型的可操控性、输出格式的可靠性和语气的一致性,还能让用户缩短提示长度,加速API调用,降低成本。本文作者SamL'Huillier对GPT-3.5与LLaMA2的微调进行了基准测试,... [详细]
赞
踩
- 一共有d个门,其中有一个门后有一只山羊,你需要需要选择s个门,然后会在另外你没有选择的门中选择e个门打开,然后你可以更换你所选择的门。问你能获取羊的最大概率。有n个座位,人依次选择座位入座,他们在选择座位时会选择尽可能距离人远的位置,不能出... [详细]
赞
踩
- 以前写过一次PHP扩展DLL,那个是利用调用系统的COM口实现的扩展,与PHP不能真正融合。心血来潮,研究了一下PHP的源码,网上找了一些资料,自己尝试写了一个扩展DLL,测试没问题。下面记录一下具体扩展方法:1、首先从www.php.ne... [详细]
赞
踩
- 【代码】cmake报错CMakeError:CouldnotfindCMAKE_ROOT。_cmakeerror:couldnotfindcmake_root!!!cmakeerror:couldnotfindcmake_root!!!原因... [详细]
赞
踩
- 总之,Spring框架提供了多种处理线程并发问题的工具和注解,开发者可以根据需要选择合适的方式来解决应用程序中的并发问题,从而提高应用程序的性能和可靠性。_springbootasync两个线程抢到了同一数据资源springbootasyn... [详细]
赞
踩
- C++作用域(一)1概述2作用域的分类2.1概述2.2名字空间作用域2.2.1名字空间的意义2.2.2名字空间的定义2.2.3名字空间成员的定义2.2.4名字空间成员的使用2.2.6标准名字空间std2.2.5名字空间的嵌套2.2.6未命名... [详细]
赞
踩



