pytorch自动求导机制

Torch.autograd

在训练神经网络时，我们最常用的算法就是反向传播（BP）。

参数的更新依靠的就是loss function针对给定参数的梯度。为了计算梯度，pytorch提供了内置的求导机制 torch.autograd，它支持对任意计算图的自动梯度计算。

• 计算图是由节点和边组成的，其中的一些节点是数据，一些是数据之间的运算
• 计算图实际上就是变量之间的关系
• tensor 和 function 互相连接生成的一个有向无环图

Tensors,Function,计算图

考虑最简单的例子，一个一层的神经网络

• input：x

• parameters：w，b

  import torch
  
  x = torch.ones(5)  # input tensor
  y = torch.zeros(3)  # expected output
  w = torch.randn(5, 3, requires_grad=True)
  b = torch.randn(3, requires_grad=True)
  z = torch.matmul(x, w)+b #x 和 w 矩阵相乘，再加上 bias b
  loss = torch.nn.functional.binary_cross_entropy_with_logits(z, y)
  1
  2
  3
  4
  5
  6
  7
  8

其计算图如下所示

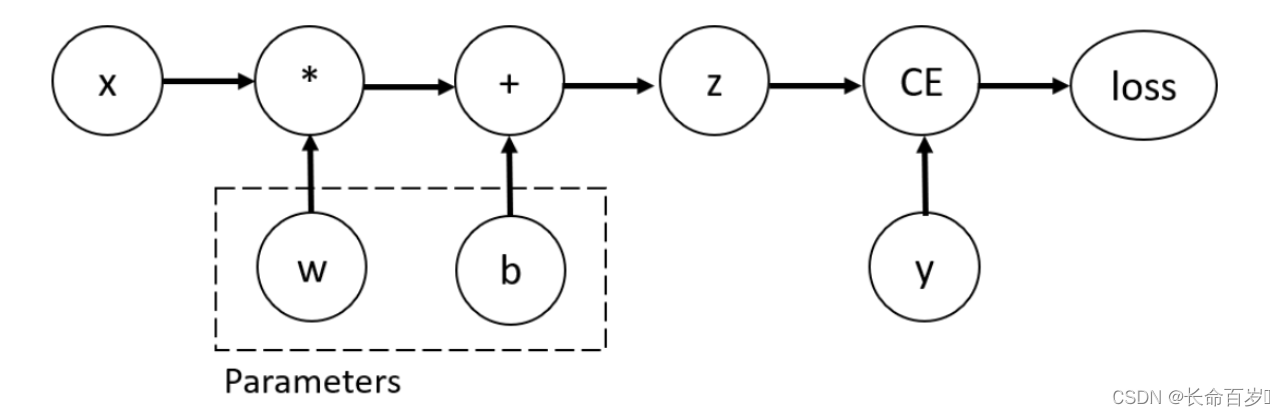
• 我们可以在创建tensor时设置 requires_grad = True 来支持梯度计算
• 也可以后续使用 x.requires_grad_(True) 来设置

我们对 tensor 应用的来构建计算图的函数，实际上是 Function 类的一个对象。

• 该对象知道如何在前向传播中实施函数

• 也知道如何在反向传播中计算梯度

• 对反向传播函数的引用存储在tensor的 grad_fn 属性中

  print('Gradient function for z =', z.grad_fn)
  print('Gradient function for loss =', loss.grad_fn)
  >>Gradient function for z = <AddBackward0 object at 0x000002A040C867F0>
  >>Gradient function for loss = <BinaryCrossEntropyWithLogitsBackward object at 0x000002A040C867F0>
  1
  2
  3
  4

计算梯度

为了更新参数，我们需要计算 loss function 关于参数的梯度。

• 我们使用 loss.backward() 来计算梯度

• 使用 w.grad，b.grad 来检索梯度值

  loss.backward()
  print(w.grad)
  print(b.grad)
  >>tensor([[0.2832, 0.0843, 0.3005],
          [0.2832, 0.0843, 0.3005],
          [0.2832, 0.0843, 0.3005],
          [0.2832, 0.0843, 0.3005],
          [0.2832, 0.0843, 0.3005]])
  >>tensor([0.2832, 0.0843, 0.3005])
  1
  2
  3
  4
  5
  6
  7
  8
  9

• note：

  • 我们仅能获得计算图叶子节点的 grad 属性，并且需要这些节点设置 requires_grad = True。对于图中的其他节点，梯度是不可获取的

  • 由于性能原因，在给定的计算图中，我们仅能使用 backward() 计算梯度一次（每次backward之后，计算图会被释放，但叶子节点的梯度不会被释放。叶子节点就是参数，不包括一些运算产生的中间变量。比如 x，w是叶子节点，但是 h = wx，h就不是叶子节点）。如果需要多次计算，我们需要设置 backward 的 retain_graph = True，这样的话求得的最终梯度是几次梯度之和

    x = torch.ones((1, 4), dtype=torch.float32, requires_grad=True)
    y = x ** 2
    z = y * 4
    loss1 = z.mean()
    loss2 = z.sum()
    loss1.backward(retain_graph=True)
    loss2.backward() #如果上面没有设置 retain_graph = True，这里会报错
    print(x.grad)
    1
    2
    3
    4
    5
    6
    7
    8

禁用梯度跟踪

有时，我们只想对数据应用模型(forward过程)，而不考虑模型的更新，这时我们可以不使用梯度跟踪

• 将计算代码包围在 torch.no_grad() 块中

  z = torch.matmul(x, w)+b
  print(z.requires_grad)
  >>True
  
  with torch.no_grad():
      z = torch.matmul(x, w)+b
  print(z.requires_grad)
  >>False
  1
  2
  3
  4
  5
  6
  7
  8

• 另一种方式是使用 detach()

  z = torch.matmul(x, w)+b
  z_det = z.detach()
  print(z_det.requires_grad)
  >>False
  1
  2
  3
  4

禁用梯度跟踪的一些原因

• fine-tune一个预训练的模型时，我们需要冻结模型的一些参数
• 当进行前向传播时，加速计算。对不追踪梯度的tensor进行计算会更高效

计算图的扩展

从概念上讲，autograd在由Function对象组成的有向无环图(DAG)中保存数据(张量)和所有执行的操作(以及产生的新张量)的记录。在DAG中，叶子是 input tensors，根是 output tensors，通过从根到叶跟踪这个图，可以使用链式法则自动计算梯度

在前向传播中，autograd同时做两件事

• 运行请求的操作来计算结果张量
• 在DAG中保持操作的梯度函数

反向传播过程开始，当 .backward() 在 DAG 根上被使用时

• 从每个 .grad_fn 中计算梯度
• 将它们累加到各个 tensor 的 .grad 属性中
• 利用链式法则，一直传播到叶子 tensor

DAGs 在 pytorch 中是动态的。值得注意的是，图是从头创建的。在每次.backward()调用之后autograd开始填充一个新的图。这正是允许我们在模型中使用控制流语句的原因，如果需要的话，我们可以在每次迭代中改变 shape（tensor的属性），size（tensor的方法） 和 operations（加减乘除等运算过程）

Tensor梯度和雅克比乘法

在很多情况下，我们loss function的结果是一个标量，我们以此来计算参数的梯度。但是，有些时候，我们的 loss 是 tensor。在这种情况下，pytorch 允许我们计算所谓的雅克比乘法，而不是梯度

• 如果是标量对向量求导(scalar对tensor求导)，那么就可以保证上面的计算图的根节点只有一个，此时不用引入grad_tensors参数，直接调用backward函数即可

• 如果是(向量)矩阵对(向量)矩阵求导(tensor对tensor求导)，实际上是先求出Jacobian矩阵中每一个元素的梯度值(每一个元素的梯度值的求解过程对应上面的计算图的求解方法)，然后将这个Jacobian矩阵与grad_tensors参数对应的矩阵相乘，得到最终的结果。v中的每个值代表该位置对应输出产生的梯度的权重。因此 v 的大小与输出 y 相同

  • 当y 和 x 都是向量时，雅克比点乘 $v^T\cdot J$ 是矩阵乘法，$v=(v_1,\dots ,v_m)$ ，$v$ 是 backward函数的参数，与 y 的大小一致。$v$ 中的每个量代表该位置对应 y 元素产生梯度的权重

    x1 = torch.tensor(1, requires_grad=True, dtype = torch.float)
    x2 = torch.tensor(2, requires_grad=True, dtype = torch.float)
    x3 = torch.tensor(3, requires_grad=True, dtype = torch.float)
    y = torch.randn(3)
    y[0] = x1 ** 2 + 2 * x2 + x3
    y[1] = x1 + x2 ** 3 + x3 ** 2
    y[2] = 2 * x1 + x2 ** 2 + x3 ** 3
    v = torch.tensor([3, 2, 1], dtype=torch.float)
    y.backward(v)
    
    print(x1.grad)
    >>tensor(10.)
    print(x2.grad)
    >>tensor(34.)
    print(x3.grad)
    >>tensor(42.)
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16

$v\circ J=\left[3\ast 2x_1+2\ast 1+1\ast 2,3\ast 2+2\ast 3x_2^2+1\ast 2x_2,3\ast 1+2\ast 2x_3+1\ast 3x_3^2\right]=[10,34,42]$

可以理解为

$v \circ J = 3 * [2x_1\,2\,1] + 2 * [1\,3x_2^2\,2x_3] + 1 * [2\,2x_2\,3x_3^2]$

- 第一项是 $y_1$ 产生的梯度，系数为 3
- 第二项是 $y_2$ 产生的梯度，系数为 2
- 第三项是 $y_3$ 产生的梯度，系数为 1
1
2
3
4
5
6
7

• 矩阵对矩阵，对应位置相乘（点乘，也是加权求和）v的大小与输出相同，每个值代表对应位置产生梯度的权重，然后相加

  • 输出是 3 * 3 的，一共 9 个输出
  • 每个输出对参数都有一个梯度矩阵，总的梯度是九个矩阵的加权

  inp = torch.tensor([[1., 0, 0], [0, 1, 0], [0, 0, 1], [1, 1, 1], [1, 1, 1]])
  w = torch.ones(3, 5, requires_grad=True)
  out = torch.matmul(w, inp)
  print(out)
  >>tensor([[3., 3., 3.],
          [3., 3., 3.],
          [3., 3., 3.]], grad_fn=<MmBackward>)
  
  x = torch.tensor([[1, 0, 0], [0, 0, 0], [0, 0, 0]]) #只考虑第一个输出产生的梯度，该梯度是一个矩阵
  out.backward(x, retain_graph=True)
  print("First call\n", w.grad)
  >>  tensor([[1., 0., 0., 1., 1.],
          [0., 0., 0., 0., 0.],
          [0., 0., 0., 0., 0.]])
  
  w.grad.zero_()
  x = torch.ones(3, 3)
  out.backward(x) # 所有输出产生的梯度权重都是 1，总的梯度为 9 个矩阵之和
  print("First call\n", w.grad)
  >> tensor([[1., 1., 1., 3., 3.],
          [1., 1., 1., 3., 3.],
          [1., 1., 1., 3., 3.]])
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13
  14
  15
  16
  17
  18
  19
  20
  21
  22

• 输出是标量的时候，v 相当于 tensor(1.0) ，可以省略