深度学习04—反向传播算法（用于参数更新、troch实现）_反向传播实例及代码

目录

1.基本原理

1.1 直接用求导的解析式来更新参数

 1.2 反向传播的原理

 1.3 tensor的存储数据以及基本应用思想

1.4 总结

2. pytorch反向传播实例

2.1 完整代码

2.2 二次模型y=w1x²+w2x+b，损失函数loss=(ŷ-y)²

2.2.1 定义参数w1,w2,b都需要计算梯度

2.2.2 定义训练模型并构建计算图

2.2.3 训练数据

---

好文推荐：

PyTorch 深度学习实践 第4讲_错错莫的博客-CSDN博客

PyTorch学习（三）--反向传播_陈同学爱吃方便面的博客-CSDN博客_pytorch 反向传播

学习地址（B站刘老师） ：
04.反向传播_哔哩哔哩_bilibili

1.基本原理

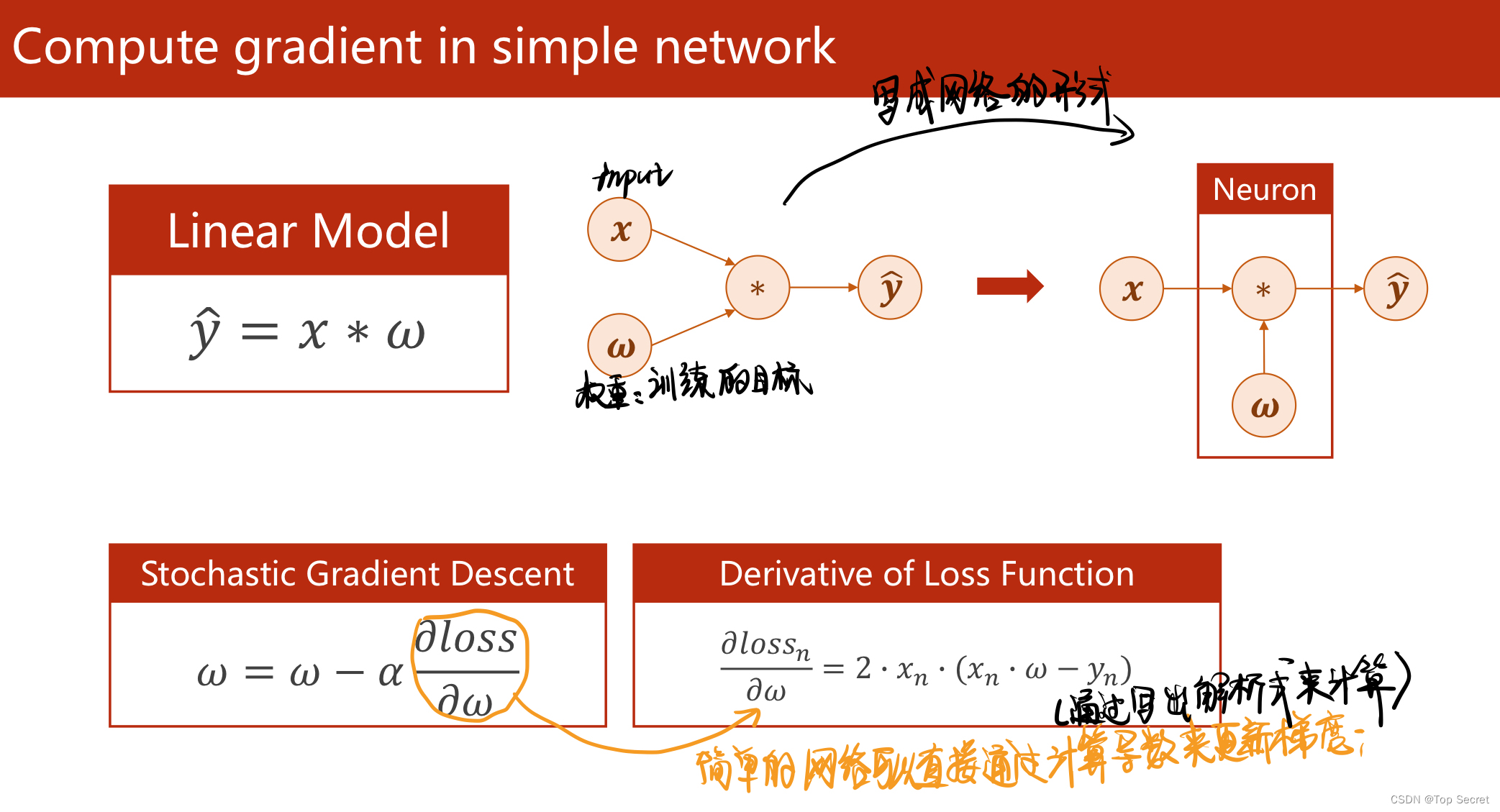
1.1 直接用求导的解析式来更新参数

 简单的网络可通过解析式表示参数更新的过程。

 对于复杂网络，利用“反向传播算法”来计算梯度；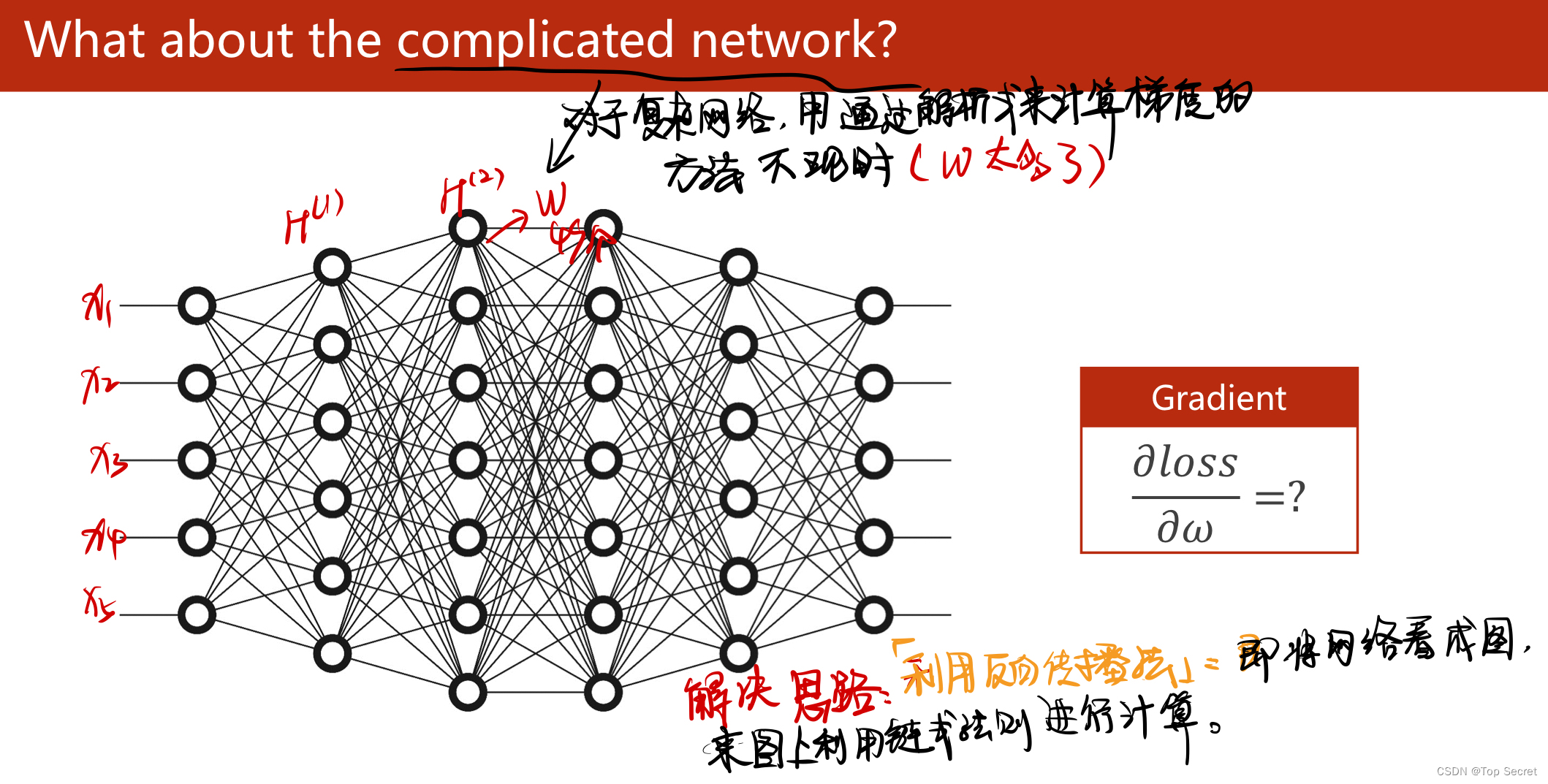

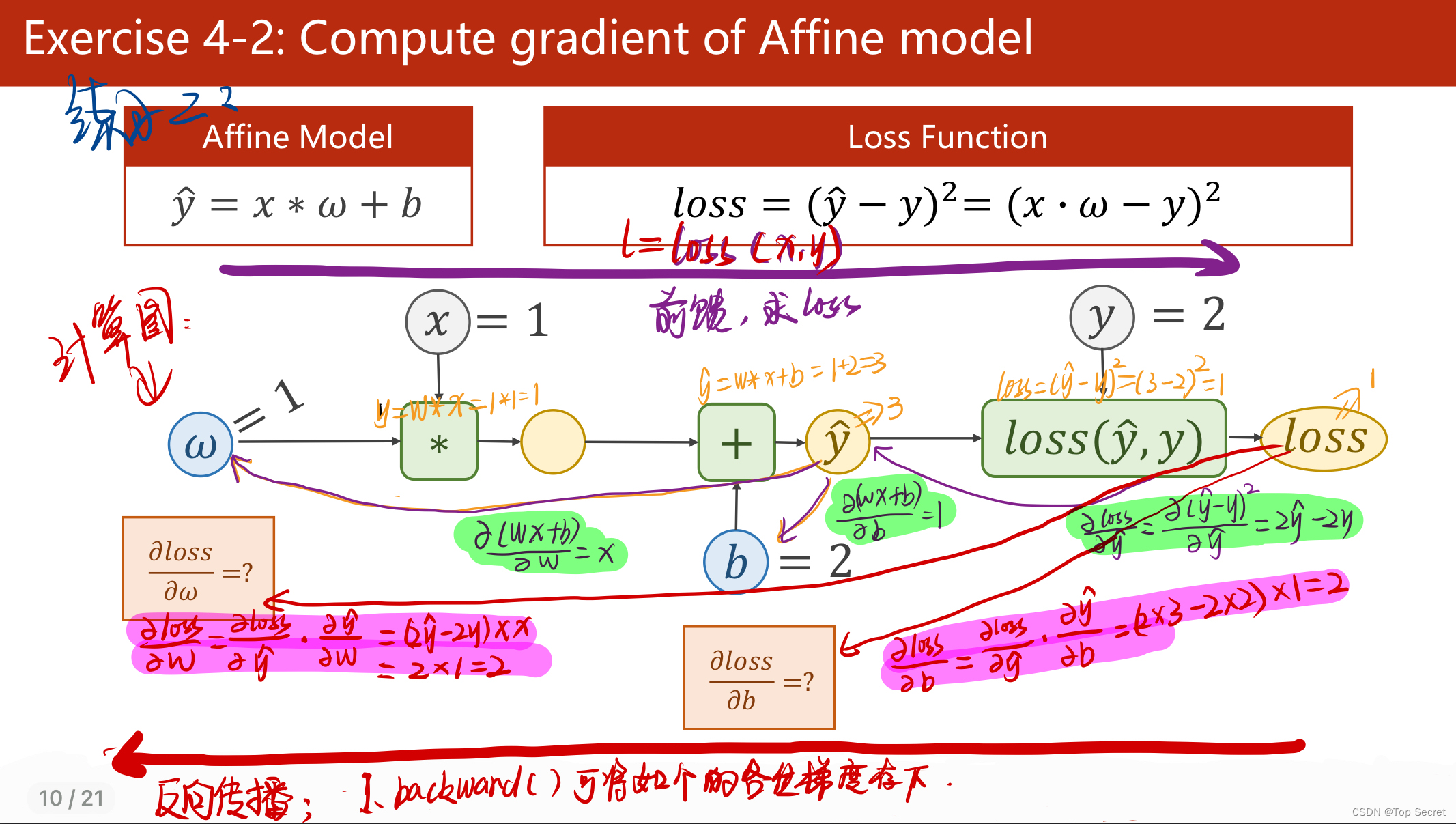
 1.2 反向传播的原理

 

 

 

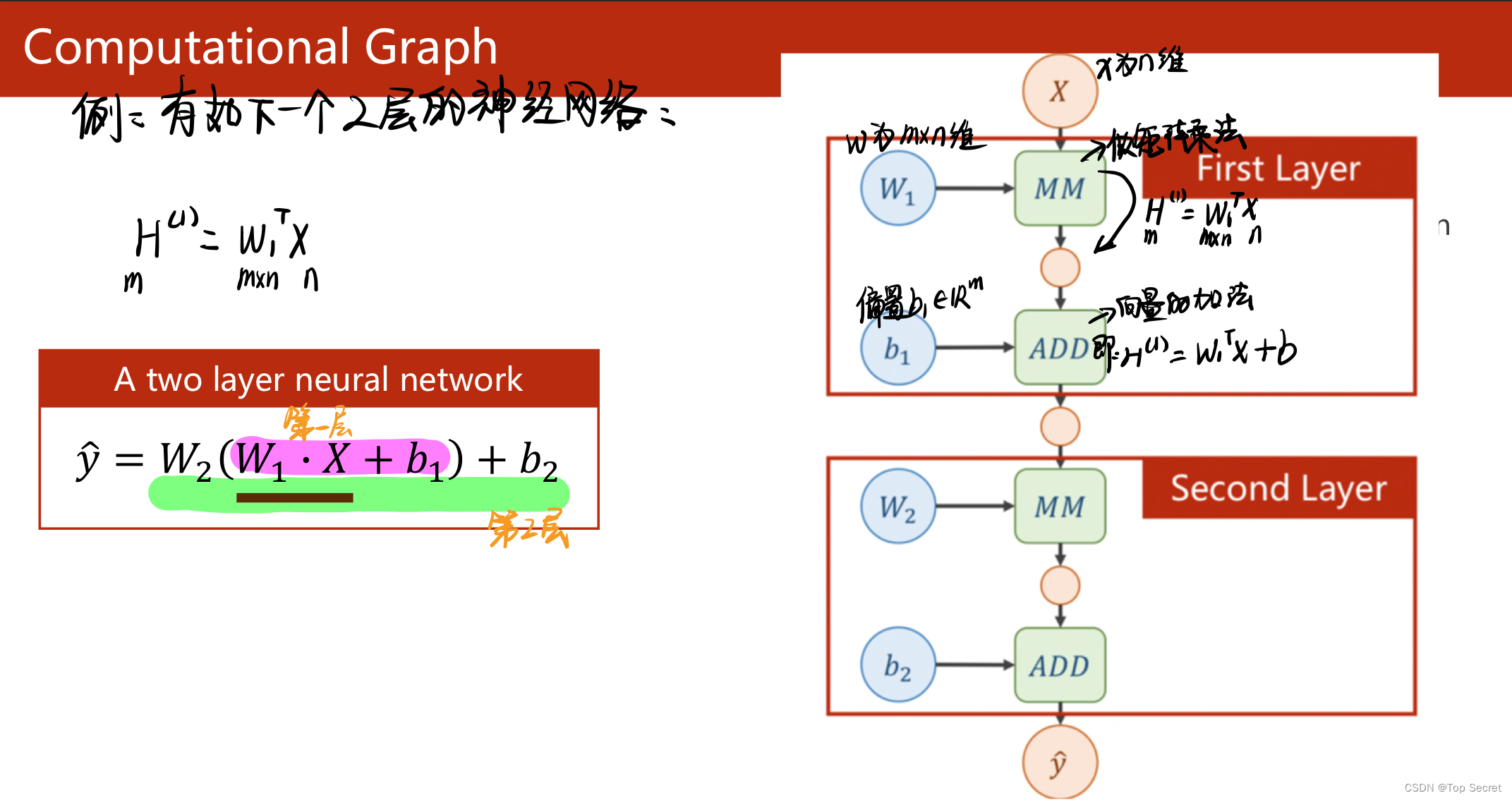
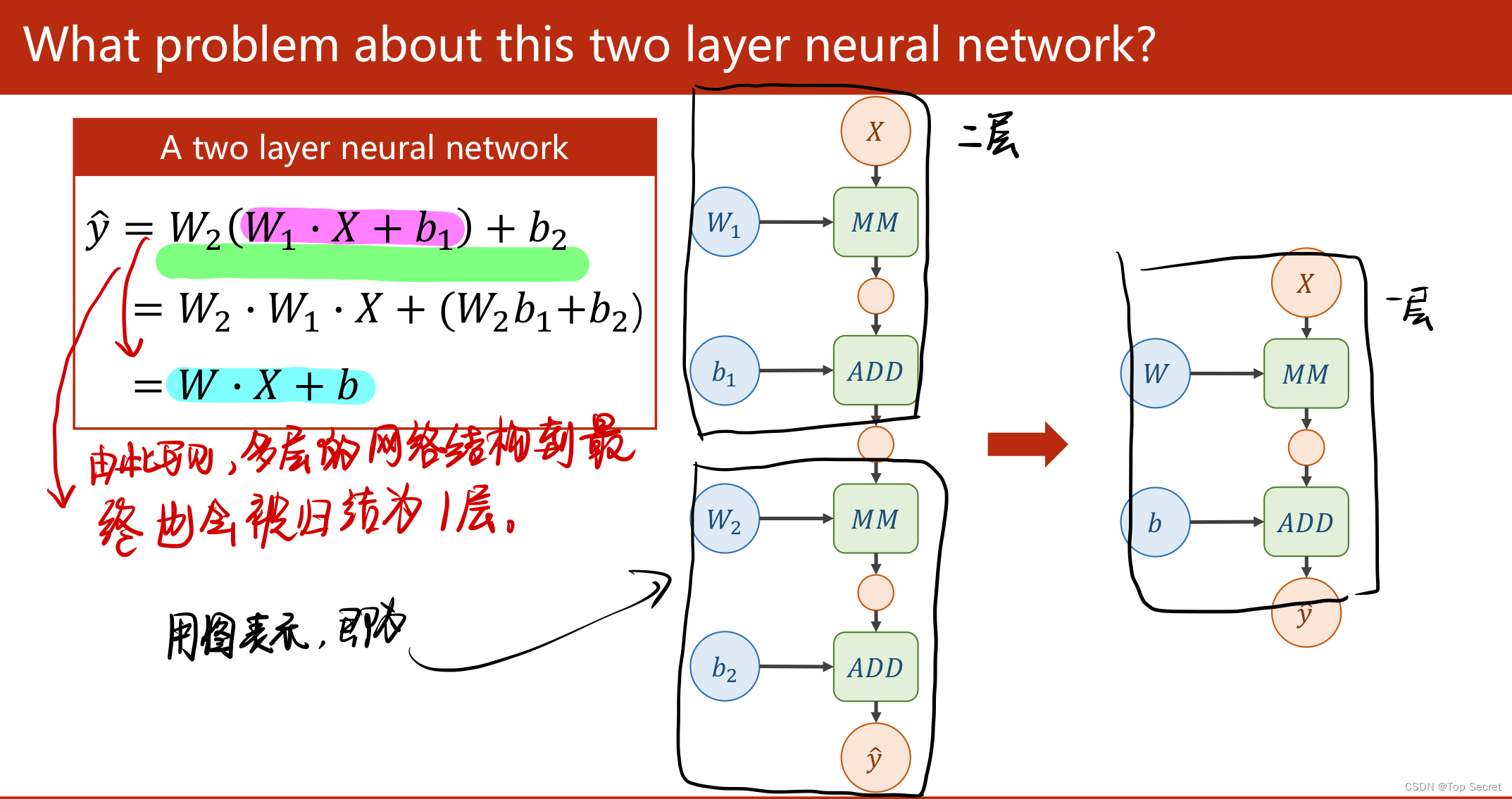
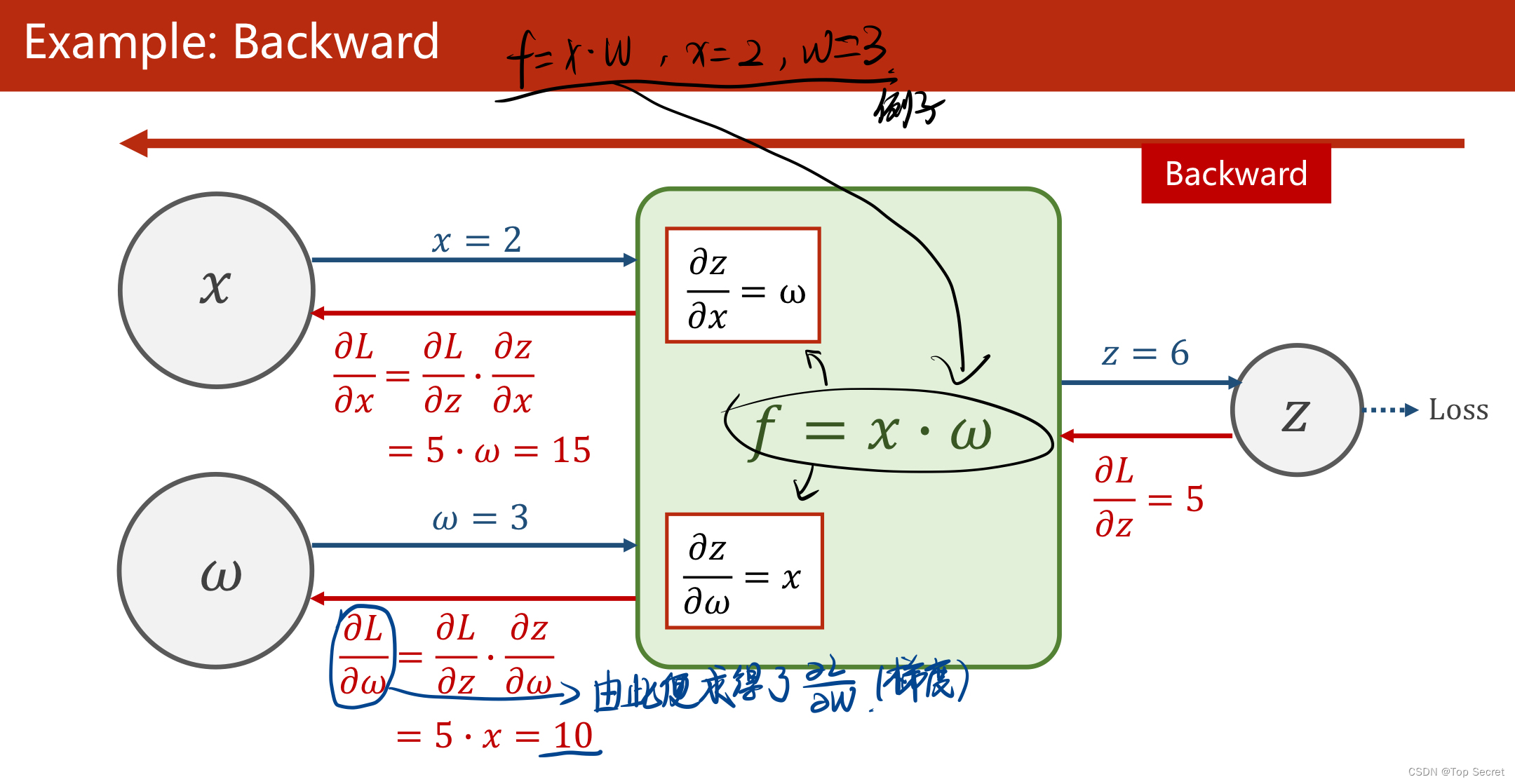
 通过分析神经网络的计算图来推演反向传播算法在参数更新中的应用。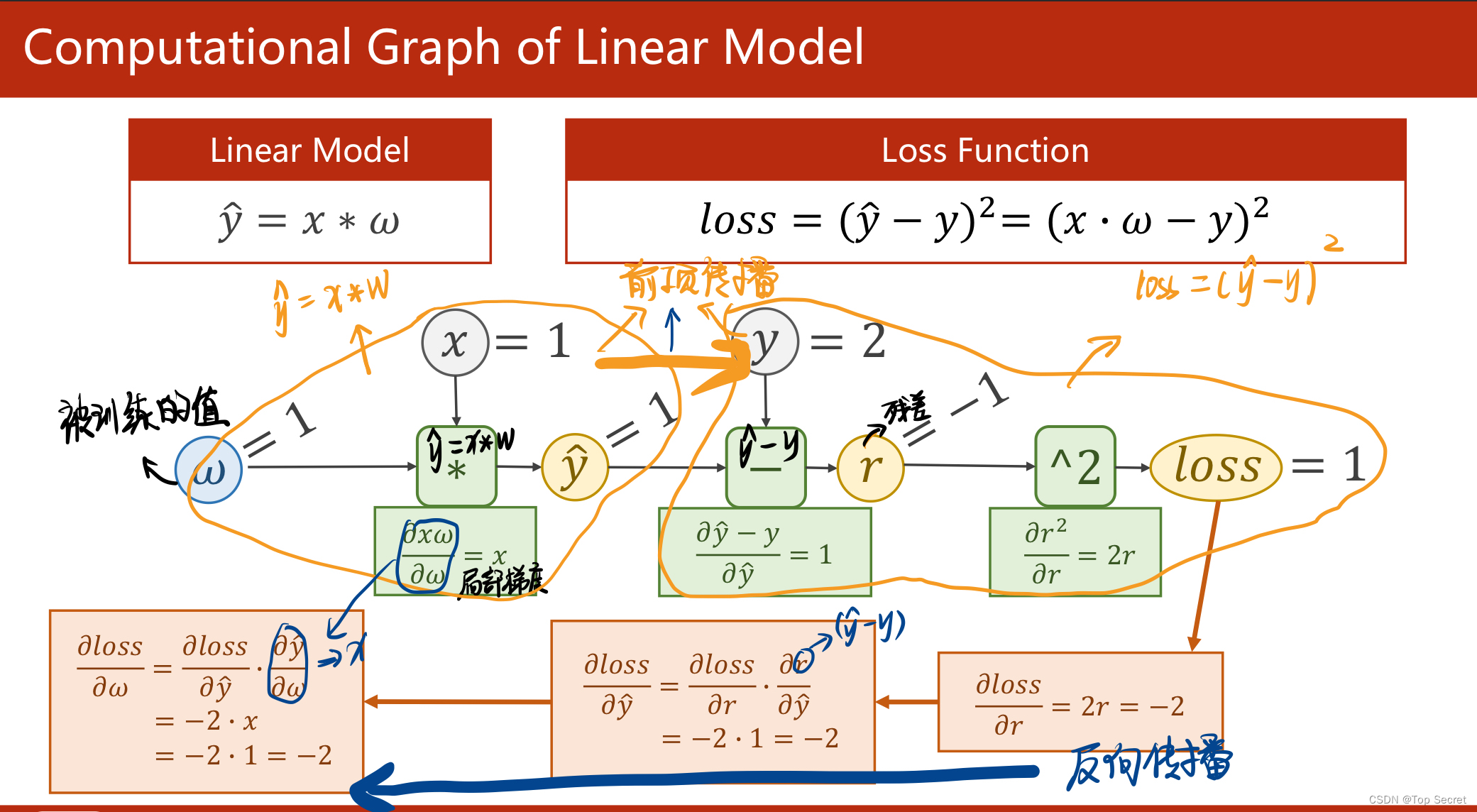

 

 

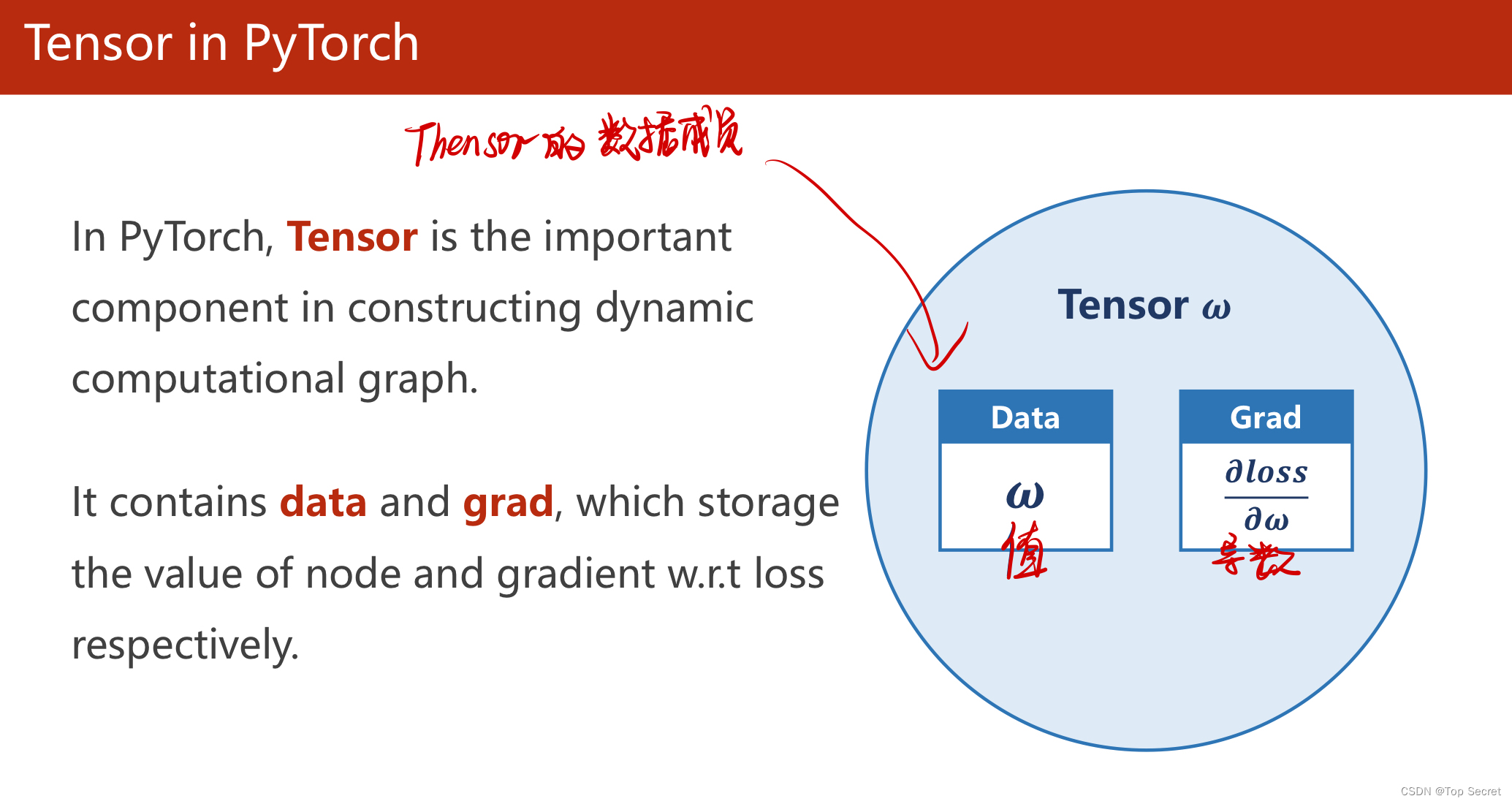
 1.3 tensor的存储数据以及基本应用思想

 

 

 

 

 

 

 

 

 

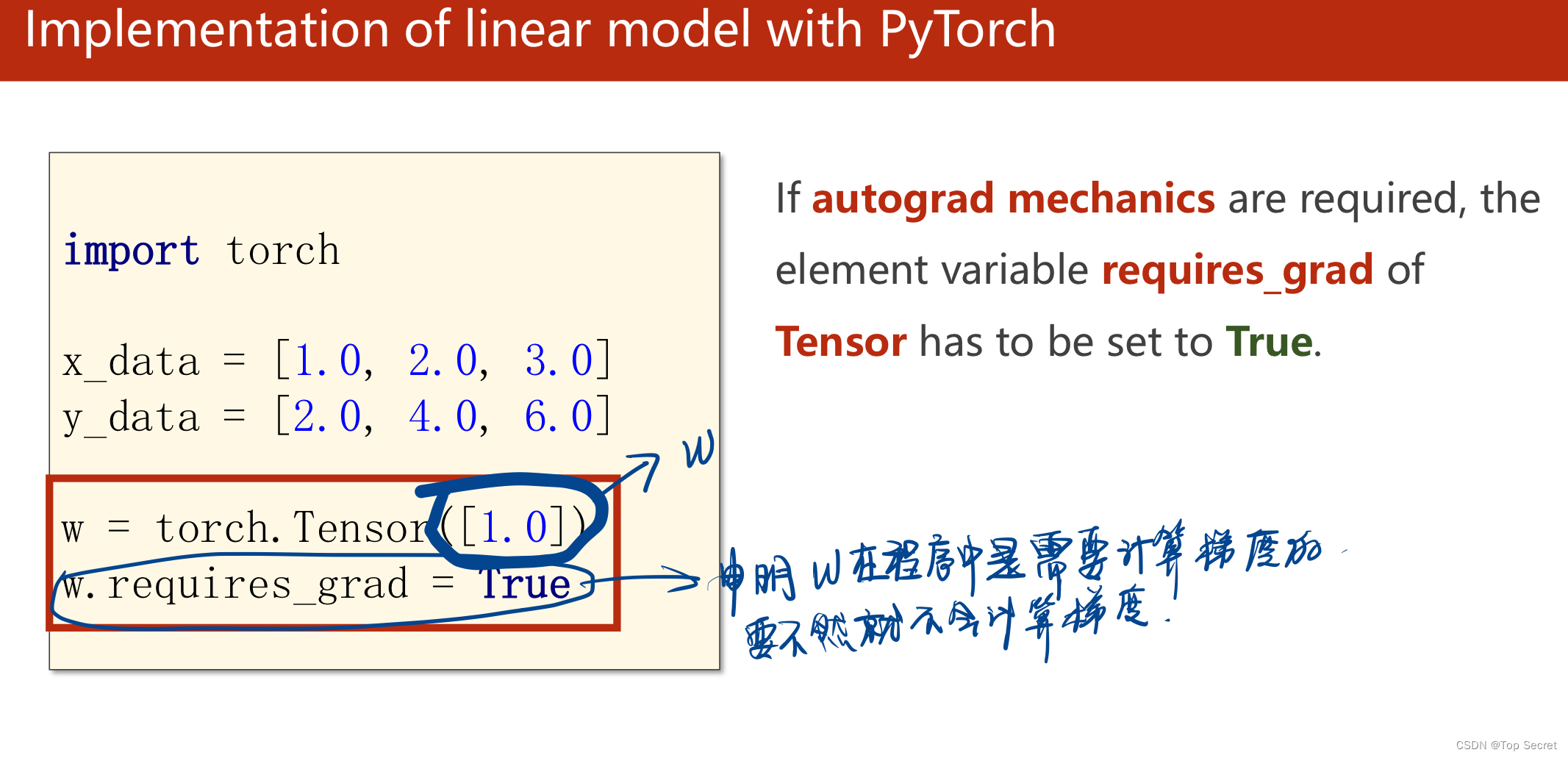
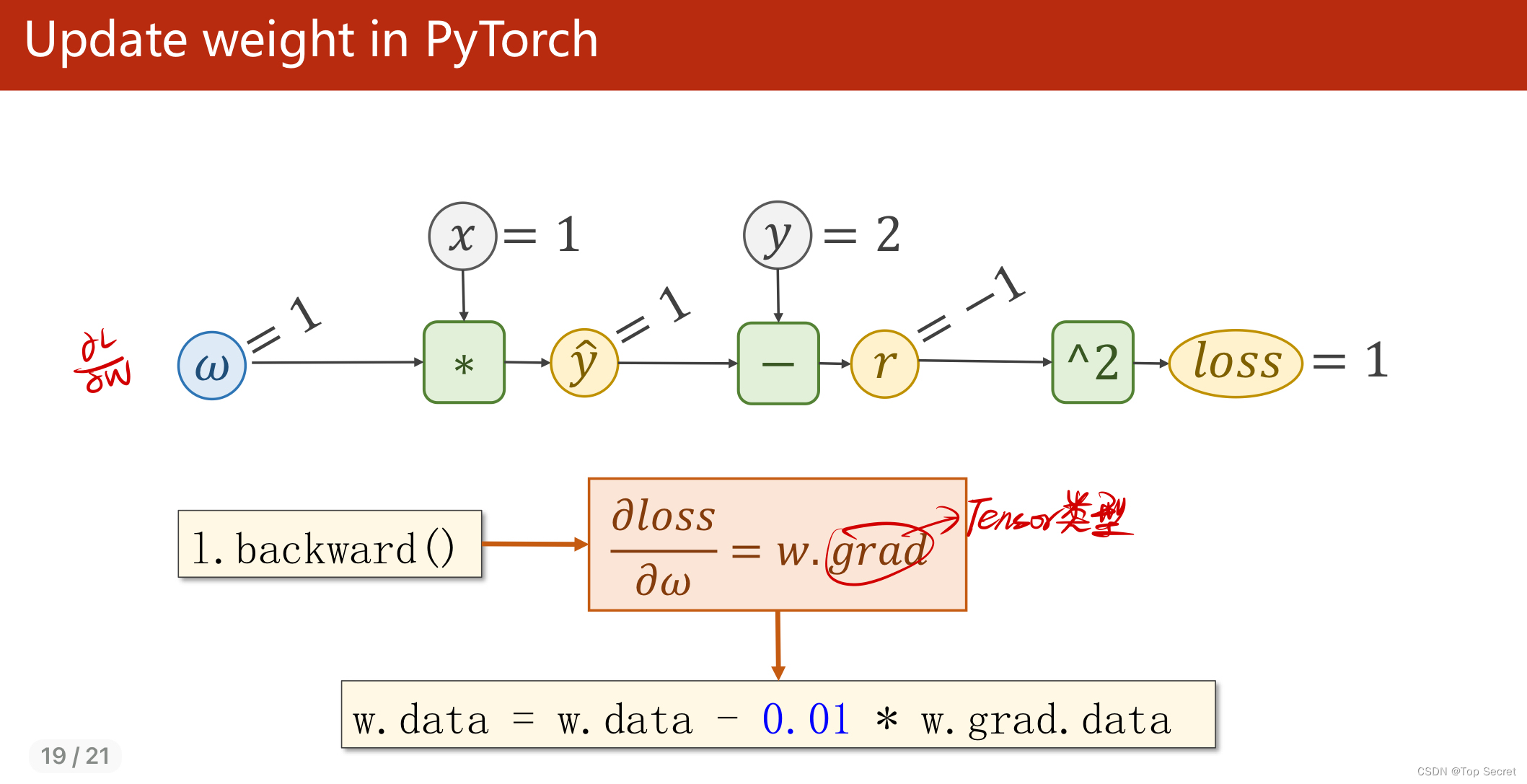
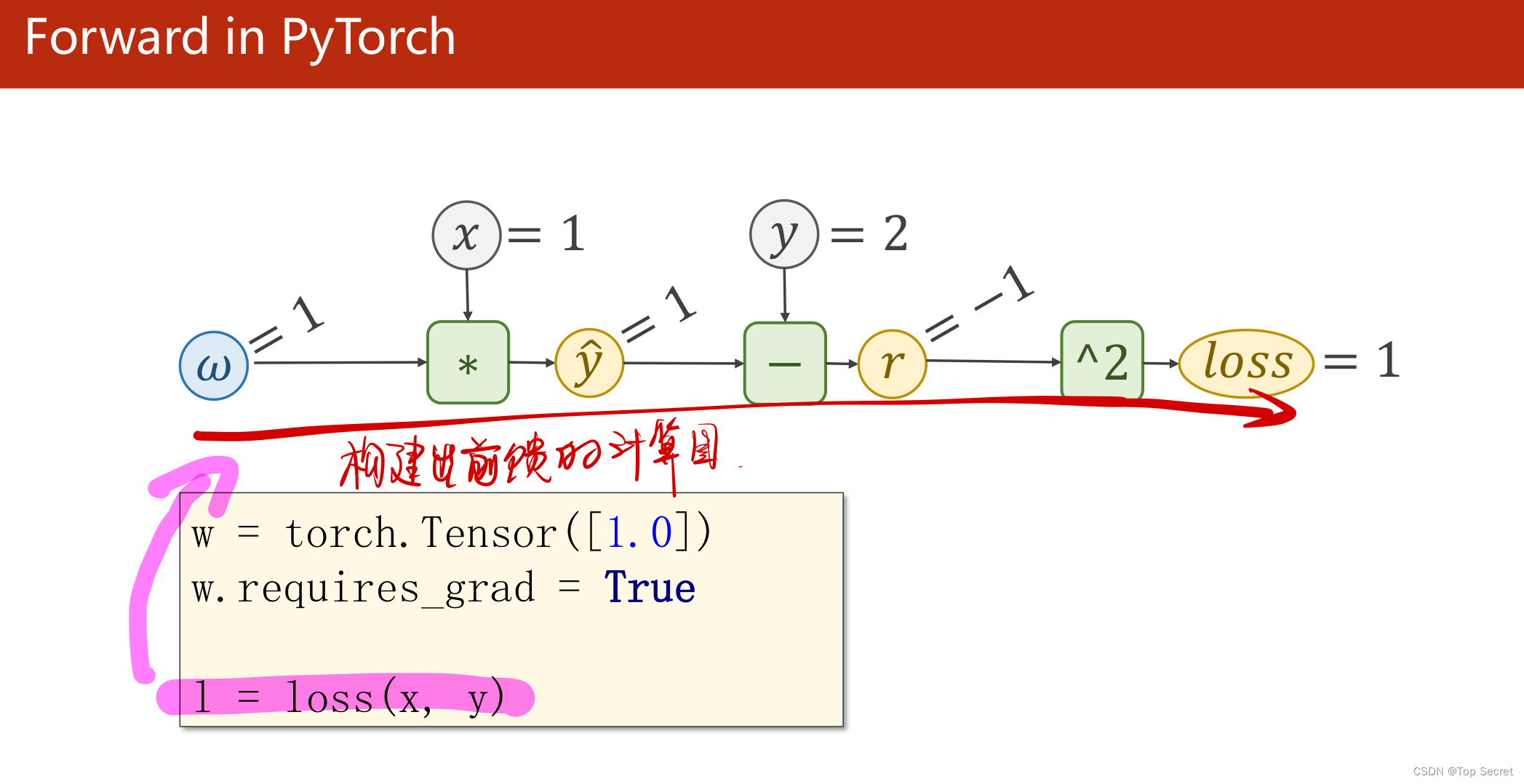
1.4 总结

（1）反向传播：该方法主要是应用链式法则的方法，求loss关于w和b的导数；

（2）关于如下步骤中，l.backward()会将前向的各部梯度存入，而红色的两个代码会形成“计算图”；

（3）其中：w是Tensor(张量类型)，Tensor中包含data和grad，data和grad也是Tensor。grad初始为None，调用l.backward()方法后w.grad为Tensor，故更新w.data时需使用w.grad.data。如果w需要计算梯度，那构建的计算图中，跟w相关的tensor都默认需要计算梯度。
 

（4）w是Tensor， forward函数的返回值也是Tensor，loss函数的返回值也是Tensor.
（5）本算法中反向传播主要体现在，l.backward()。调用该方法后w.grad由None更新为Tensor类型，且w.grad.data的值用于后续w.data的更新。l.backward()会把计算图中所有需要梯度(grad)的地方都会求出来，然后把梯度都存在对应的待求的参数中，最终计算图被释放。取tensor中的data是不会构建计算图的。

2. pytorch反向传播实例

前置：由torch.tensor()创建tensor类型数据；

import torch
a = torch.Tensor([1.0])
a.requires_grad = True # 或者 a.requires_grad_()
print(a)
print(a.data)
print(a.type())             # a的类型是tensor
print(a.data.type())        # a.data的类型是tensor
print(a.grad)
print(type(a.grad))
 
"""
C:\Users\ZARD\anaconda3\envs\PyTorch\python.exe C:/Users/ZARD/PycharmProjects/pythonProject/机器学习库/PyTorch实战课程内容/backward.py
tensor([1.], requires_grad=True)
tensor([1.])
torch.FloatTensor
torch.FloatTensor
None
<class 'NoneType'>
Process finished with exit code 0
"""

2.1 完整代码

import torch
 
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
 
w = torch.tensor([1.0])  # w的初值为1.0，是一个tensor
w.requires_grad = True  # 指明参数w需要计算梯度
 
# 定义一个线性模型：y=x*w
def forward(x):
    return x * w  # w是一个Tensor
 
#计算损失函数，算出的loss的数据类型为tensor
def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) ** 2
 
print("predict (before training)", 4, forward(4).item()) #打印初始值
 
#训练数据100次
for epoch in range(100):
    for x, y in zip(x_data, y_data):
        l = loss(x, y)  # l是一个张量，tensor主要是在建立计算图 forward, compute the loss
        l.backward()  # backward,compute grad for Tensor whose requires_grad set to True
        print('\tgrad:', x, y, w.grad.item())
        w.data = w.data - 0.01 * w.grad.data  # 权重更新时，注意grad也是一个tensor
        #每一次数据的参数更新完成后，都需要对计算图中的梯度记录做一次清理，要不然在下一组数据的更新中将这次的参数与下一次叠加在一起
        w.grad.data.zero_()  # after update, remember set the grad to zero
 
    print('progress:', epoch, l.item())  # 取出loss使用l.item，不要直接使用l（l是tensor会构建计算图）
 
print("predict (after training)", 4, forward(4).item())

运行结果：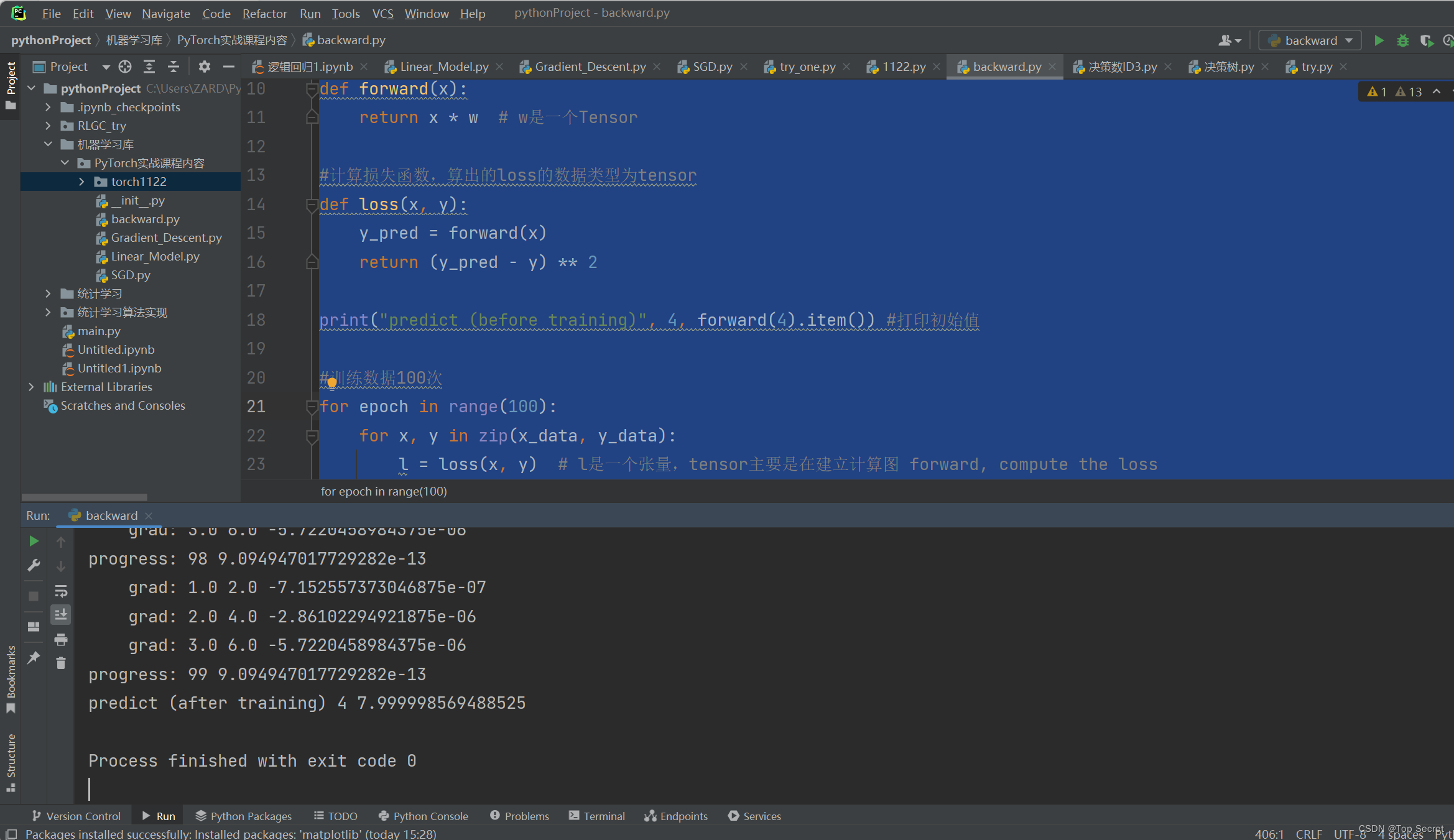

2.2 二次模型y=w1x²+w2x+b，损失函数loss=(ŷ-y)²

画出该模型的计算图：

参考文章，侵删：https://blog.csdn.net/weixin_44841652/article/details/105046519

2.2.1 定义参数w1,w2,b都需要计算梯度

#模型：y = w1 * x**2 + w2 * x + b
 #如下定义参数w1,w2,b都需要计算梯度
w1 = torch.Tensor([1.0])#初始权值
w1.requires_grad = True#计算梯度，默认是不计算的
w2 = torch.Tensor([1.0])
w2.requires_grad = True
b = torch.Tensor([1.0])
b.requires_grad = True

2.2.2 定义训练模型并构建计算图

# 定义模型：y = w1 * x**2 + w2 * x + b
def forward(x):
    return w1 * x**2 + w2 * x + b
 
def loss(x,y):#构建计算图，计算loss
    y_pred = forward(x)
    return (y_pred-y) **2

2.2.3 训练数据

#训练数据100次
for epoch in range(100):
    l = loss(1, 2)#为了在for循环之前定义l,以便之后的输出，无实际意义
    for x,y in zip(x_data,y_data):
        #step1: 计算loss，l.backward()构建计算图；
        l = loss(x, y)
        l.backward()
        print('\tgrad:',x,y,w1.grad.item(),w2.grad.item(),b.grad.item())
        
        #step2: 参数更新,并释放各参数对应的梯度
        w1.data = w1.data - 0.01*w1.grad.data #注意这里的grad是一个tensor，所以要取他的data
        w2.data = w2.data - 0.01 * w2.grad.data
        b.data = b.data - 0.01 * b.grad.data
        # 释放之前计算的梯度（如下可见，释放的梯度是相对与每一个需要被计算梯度的tensor数据相对应的）
        #因此，简记为： w1.requires_grad = True 与 w1.grad.data.zero_() 成对出现
        w1.grad.data.zero_()
        w2.grad.data.zero_()
        b.grad.data.zero_()
        
        #step3:输出每次训练的损失
    print('Epoch:',epoch,l.item()) #读取每一次训练得到的loss值，用l.item()

该过程可以简单总结为3部分：

（1）计算loss，l.backward()构建计算图； 

（2）参数更新,并释放各参数对应的梯度；

（3）输出每次训练的损失；

输出：

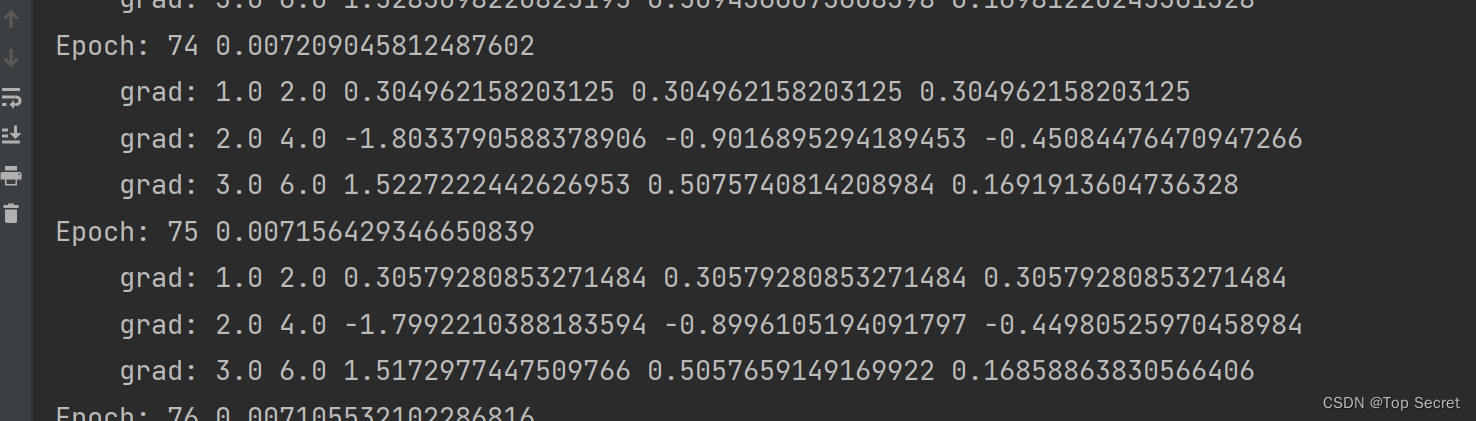
复盘总结：
理论的Tips:

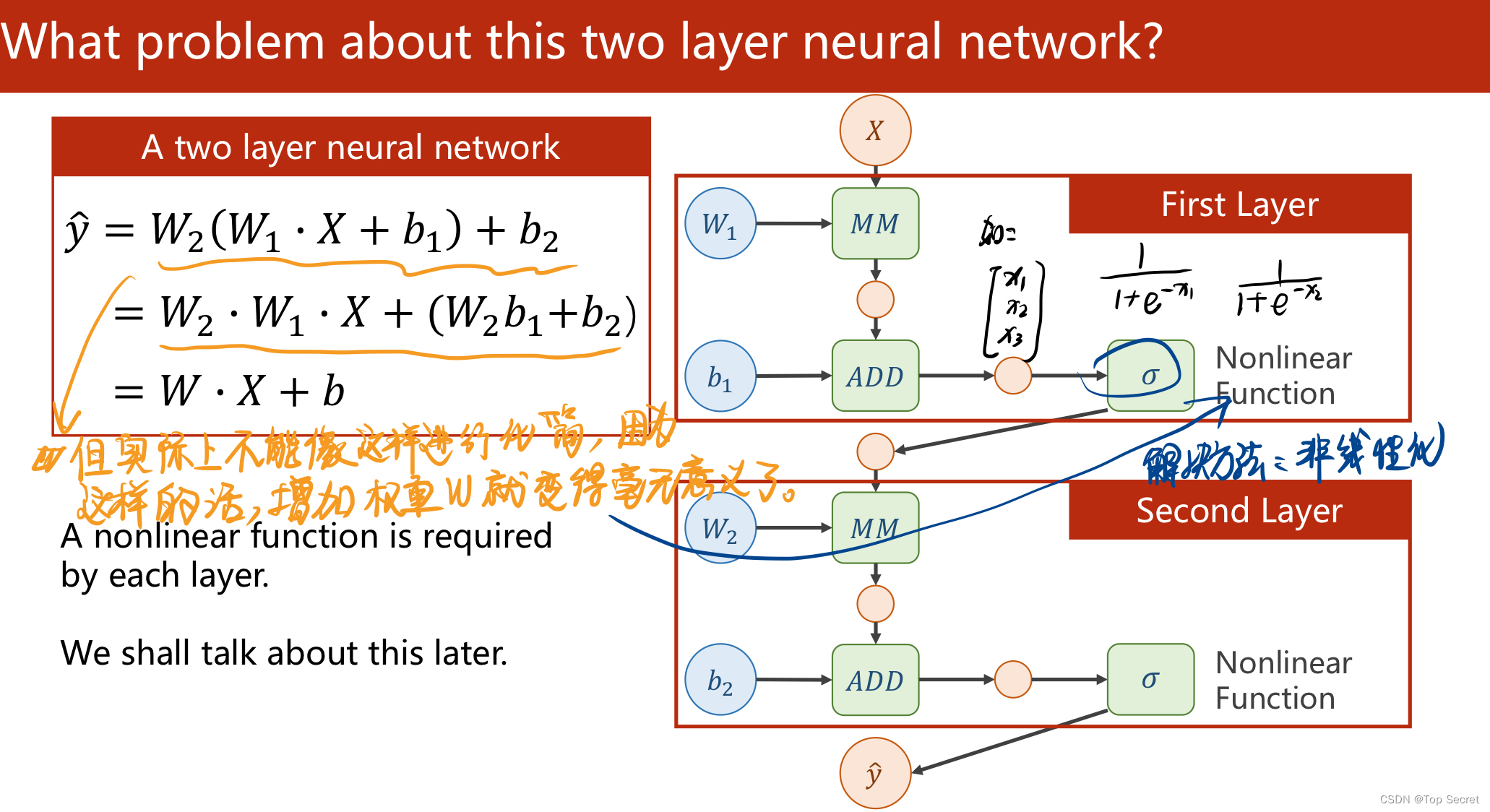
（1）对于简单的网络，可通过解析式表示参数更新的过程；
（2）对于复杂网络，利用“反向传播算法”来计算梯度；
（3）通过分析神经网络的计算图来推演反向传播算法在参数更新中的应用。 （先分析前馈过程，再分析反向传播的过程）

编程的Tips:
(1) 对于某个需要计算导数的张量，比如权重w，在定义好w后，要声明需对其计算梯度，语法是：w.requires_grad = True