数据降维之因子分析_caith数据集 眼睛和头发

之前学习的时候大略看了一下，不记得什么，重新学习学习

因子分析(factor analysis

是主成分分析的推广和发展，与主成分分析 一样，它也是一种”降维”的统计分析方法。是一种用来分析隐藏在表面现象背后的因子作用的一类统计模型。

因子分析是研究相关阵或协方差阵的内部依赖关系，它将多个变量综合为少数几个因子，以再现原始变量与因子之间的关系。

因子分析的主要应用有两个方面：一是寻求基本结构，简化观测系统， 将具有错综复杂关系的对象（变量或样本）综合为少数几个因子（不 可观测的随机变量），以再现因子与原始变量之间的内在联系；二是 用于分类，对于p个变量或n个样本进行分类

因子分析根据研究对象的不同可以分为R型和Q型因子分析。

R型因子分析研究变量(指标)之间的相关关系，通过对变量的相关阵或 协方差阵内部结构的研究，找出控制所有变量的几个公共因子(或称主 因子、潜在因子)，用以对变量或样本进行分类。

Q型因子分析研究样本之间的相关关系，通过对样本的相似矩阵内部结

构的研究找出控制样本的几个主要因素(或称为主因子)。

这两种因子分析的处理方法是一样的，只是出发点不同。R型从变量的

相关阵出发，Q型从样本的相似矩阵出发。

因子的特点：

1） 因子变量的数量远远少于原始变量的个数；

2） 因子变量并非原始变量的取舍，而是一种新的综合；

3） 因子变量之间没有线性关系；

4） 因子变量具有明确的解释性，可以最大限度地发挥专业分析的作用。

因子分析就是以最小的信息损失，将众多的原始变量浓缩成为少数几个

因子变量，使得变量具有更高的可解释性的一种数据缩减方法。

因子分析的核心问题有两个：一是如何构造因子变量，二是如何对因子 变量进行命名解释。

因子分析常常有以下四个基本步骤：

1） 确定待分析的原变量是否适合做因子分析。

2） 构造因子变量。

3） 利用旋转方法使因子变量更具有可解释性。

4） 计算因子变量得分。

 

1） 将原始数据标准化，以消除变量间在数量级和量纲上的不同。

2） 求标准化数据的相关矩阵。

3） 求相关矩阵的特征值和特征向量。

4） 计算方差贡献率与累积方差贡献率。

5） 确定因子：设F1、F2、…,Fp为p个因子，其中前m个因子包含的数据信 息总量(即其累积贡献率)不低于80%，可取前m个因子来反映原评价指标。

6） 因子旋转：若所得的m个因子无法确定或其实际意义不是很明显，这时

需要因子进行旋转以获得较为明显的实际含义。

7） 用原指标的线性组合来求各因子得分：采用回归估计法、Bartlett估计法

计算因子得分。

8） 综合得分：以各因子的方差贡献率为权，由各因子的线性组合得到综合

评价指标函数：

9） 得分排序：利用综合得分可以得到得分名次。

R中自带的因子分析函数factanal()采用极大似然估计方法估计因子载荷，适

用于大样本量的数据分析，其调用格式为

factanal(x, factors, data = NULL, covmat = NULL, n.obs = NA, subset, na.action, start = NULL, scores = c("none", "regression", "Bartlett"), rotation = "varimax", control = NULL, ...)

x是公式或用于因子分析的数据，可以是矩阵(每行为一个样本)或数据框； factors表示要生成的因子个数；data指定数据集；当x为公式时使用； covmat是样本的协方差矩阵或相关系数矩阵，使用这个参数时x可以忽略； scores表示计算因子得分的方法；rotation表示因子旋转的方法，默认 为”varimax”—方差最大旋转。

例：洛杉矶街区数据(LA.Neighborhoods.csv)，这是美国普查局2000年的数据。一共有110个街区，15个变量。

 

w=read.csv("LA.Neighborhoods.csv") #读入数据 
w$density=w$Population/w$Area	#增加人口密度变量
u=w[,-c(12:15)] #去掉人口、面积、经纬度变量
(a=factanal(factors=2,scale(u[,-1]),scores="regression"))
 
plot(a$scores[,1:2],type="n",ylim=c(-2,1.5),xlim=c(-2.5,2.5),
xlab="Factor 1",ylab="Factor 2",main="Factor Scores")
abline(h=0);abline(v=0)
text(a$scores[,1],a$scores[,2],labels=u[,1],cex=0.7)
 

 

因子得分图各个点是用街区名字代表的， 从图中可以看出各种街区所在的位置， 也可以识别一些特别突出的街区。

对应分析把R型因子分析和Q型因子分析统一起来，通过R型因子分析直 接得到Q型因子分析的结果，同时把变量(指标)和样品反映到相同的坐 标轴(因子轴)的一张图上，以此来说明变量(指标)与样品之间的关系。

对应分析应用于分类变量而不是连续变量，传统意义上应用于列联表， 但由于其实描述性的，其他表格也可以应用。所有数据都应该是非负的， 并且行和列是平等的。

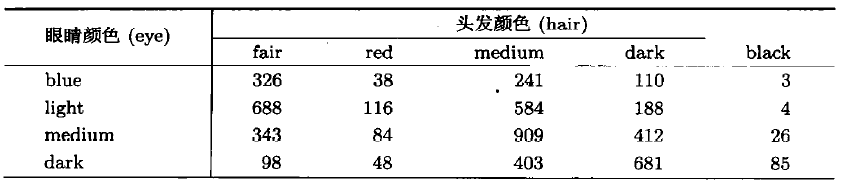
眼睛和头发颜色数据(caith.txt) 该数据是关于苏格兰Caithness地方人 的眼睛颜色(变量eye)和头发颜色(变量hair)的列联表。该地引人关注是 因为那里混居着北欧日耳曼人(Nordic)，凯尔特人(Celtic)和盎格鲁撒拉 逊人(Anglo-Saxon)。

数据见下表：

library(MASS)
 
v=caith	#数据来源
colnames(v)=paste(colnames(v),"hair") rownames(v)=paste(rownames(v),"eye") (cc=corresp(v,nf=2)) #对应分析集结果输出

 

 

输出的是典型相关系 数，行计分和列计分

颜色深的眼睛和颜色深的头发接近，反之亦然