2021年认证杯SPSSPRO杯数学建模B题(第一阶段)依巴谷星表中的毕星团求解全过程文档及程序_恒星视星等spss

2021年认证杯SPSSPRO杯数学建模

B题 依巴谷星表中的毕星团

原题再现：

  依巴谷卫星（High Precision Parallax Collecting Satellite，缩写为 Hip-parcos），全称为“依巴谷高精度视差测量卫星”，是欧洲空间局发射的一颗天体测量卫星，用以精确测量恒星的视差和自行。通过视差可以推断出恒星距地球的距离。
  毕星团位于金牛座，是离地球最近的疏散星团。其成员星在 300 个以上，有多颗肉眼可见的亮星。对毕星团的研究已经持续了许多年，包括确定它的距离，构建演化的模型，确认或排除成员，以及研究各成员星的特性等。依据依巴谷卫星的观测数据，我们可以以相当高的精度测量相关各星的距离和运动情况，以对毕星团进行更加精确的研究。
  在依巴谷卫星的观测数据中，毕星团中的亮星平均视差在 22 毫角秒左右，意味着其平均距离在 45 秒差距左右。我们在依巴谷星表中选择了 2719颗恒星，选择的标准是视差在 20–25 毫角秒之间（也就是距离地球在 40–50秒差距之间），其中包括了许多毕星团的成员。
  这个数据集有如下字段：
  1. HIP：星体编号
  2. Vmag：视星等
  3. RA：赤经（度）
  4. DE：赤纬（度）
  5. Plx：视差角（毫角秒），1000/Plx 即为目标离观测点的距离（秒差距）
  6. pmRA：恒星自行的 RA 分量（毫角秒/年）
  7. pmDE：恒星自行的 DE 分量（毫角秒/年）
  8. e_Plx：Plx 的测量误差（毫角秒）
  9. B-V：恒星的色指数
  第一阶段问题： 请你建立合理的数学模型，在数据集中确认毕星团的成员星，并绘制出毕星团成员星的赫–罗图。

整体求解过程概述(摘要)

  依巴谷卫星中记载了大量高精度的恒星位置、自行和视差等天体信息，毕星团作为距离地球最近的疏散星团，找出毕星团的成员星并绘制赫罗图在宇宙学研究中具有重要的科学意义。本文主要建立了基于改进的 DBSCAN 算法的 OPTICS 聚类模型，根据恒星自行的距离、方向及所在位置找出了毕星团的成员星，并绘制了毕星团的赫罗图。
  针对问题一，要求在数据集中确认毕星团的成员星。首先我们对附件数据进行描述性统计分析，发现恒星赤经赤纬和自行分量的数据标准偏差较大，所以我们对这 4 种变量数据进行正态性分布检验，利用拉依达法则剔除离散程度较大的数据。然后我们将变量数据进行标准化处理，选择基于密度的 DBSCAN 聚类方法，为了降低 DBSCAN 算法对初始参数领域半径和阈值的敏感性，我们对 DBSCAN 算法进行改进，引入核心距离和可达距离两个概念，采用 OPTICS 聚类模型并根据恒星自行的距离、方向及所在位置进行聚类，得到 331 颗毕星团的成员星。最后以毕星团满足球状为依据对毕星团的成员星进行了验证。
  针对问题二，要求绘制出毕星团成员星的赫罗图。首先我们通过查阅文献了解赫罗图的相关信息。然后我们根据视星等和恒星距观测点距离这两种数据计算出恒星的绝对星等，得到赫罗图的纵轴数据，并采用附件给出的色指数作为横轴数据。最后我们利用Matlab 和 PowerPoint 对照文献中的标准赫罗图绘制出毕星团的赫罗图。最后，深入研究了论文中提出的模型并加以分析，指出了模型存在的优缺点，对模型的优化提出了改进思路。

模型假设：

  为使解题过程得到简化，本文做出如下假设以规定模型的适用范围。
  （1）假设附件相关数据可靠，且其中的奇异数据和缺省值忽略后对总体信息不会有显著性影响；
  （2）假设星团和星团之间的距离远大于星团内部成员星之间的距离；
  （3）假设在测量期间内恒星距观测点的距离几乎不变；
  （4）假设毕星团成员星满足金牛座星团球状分布规律。

问题分析

  针对第一问，要求在数据集中确认毕星团的成员星。为了更好地了解附件数据信息，首先我们对附件数据进行描述性统计分析，找出便于描述测量样本的各种特征及数据之间的内在规律。我们认为附件数据庞大并且字段种类较多，有必要对标准偏差较大的数据进行离群点检测，为了方便选择去噪的方法，我们还要对数据进行正态性分布检验，然后对通过检验的字段使用拉依达准则剔除异常值。处理完数据后将变量数据进行标准化处理，来消除在聚类时数据因大小不一而造成的偏差，至此，模型的准备工作已经结束，接下来可以构建毕星团成员星的聚类模型。聚类模型我们选择基于密度的聚类方法，其中 DBSCAN 算法有着速度快、聚类簇的形状没有偏倚、无需设置聚类个数等种种优点，但是它的对于初始参数领域半径和阈值的取值非常敏感，所以我们对 DBSCAN 算法进行改进，采用 OPTICS 聚类模型对成员星进行聚类，并根据恒星自行的距离、方向及所在位置进行聚类，从而可以得到毕星团的成员星，由于毕星团的是球状星，所以最后可以查找球状星的相关资料来验证成员星的可靠性。
  针对第二问，要求绘制出毕星团成员星的赫罗图。赫罗图是指恒星的光谱类型与光度之关系图。赫罗图的纵轴是光度与绝对星等，而横轴则是光谱类型及恒星的表面温度。由于视星等和光度的对数成正比，恒星的色指数附件数据已经给出，所以我们只需要计算出成员星的绝对星等，最后根据文献中的标准赫罗图对我们自己画的初步赫罗图进行补全相关信息等工作。
  本文主要通过在数据集中确认毕星团的成员星，并绘制出毕星团成员星的赫罗图。本文研究的技术路线如图 2 所示。

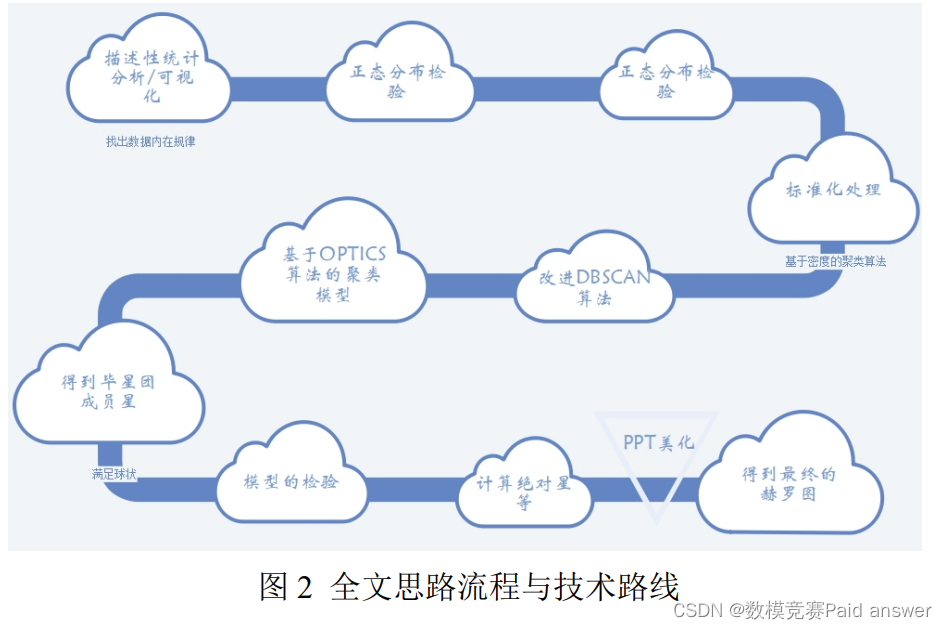
模型的建立与求解

  为了更好地了解附件数据信息，首先我们利用 SPSS 对附件数据进行描述性统计分析，找出便于描述测量样本的各种特征及数据之间的内在规律，得到的统计数据如表 2所示。

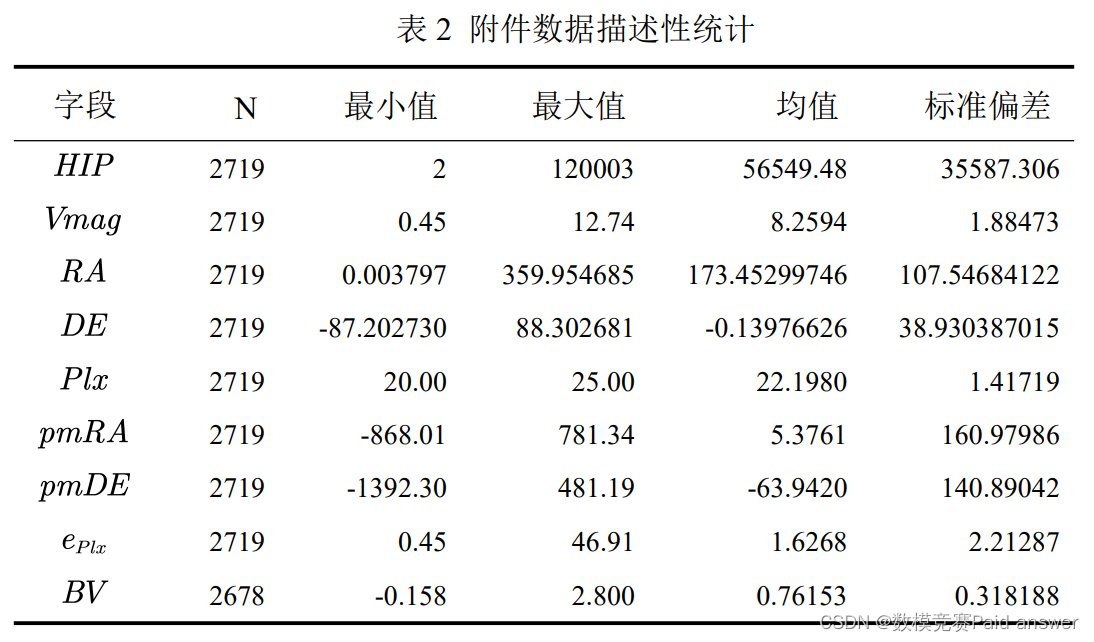
  通过对表 2 进行分析，我们可以发现恒星的 BV 字段总共缺失了 41 条数据，其他字段数据没有缺失值；恒星的 RA、DE、pmRA 和pmDE这4组数据的标准偏差比较大，说明这几个字段自身之间的离散程度程度比较大，还需要通过进行离群点检测，所以我们利用 Excel 绘制带直线的散点图观察其平面分布情况，如图 3 所示。

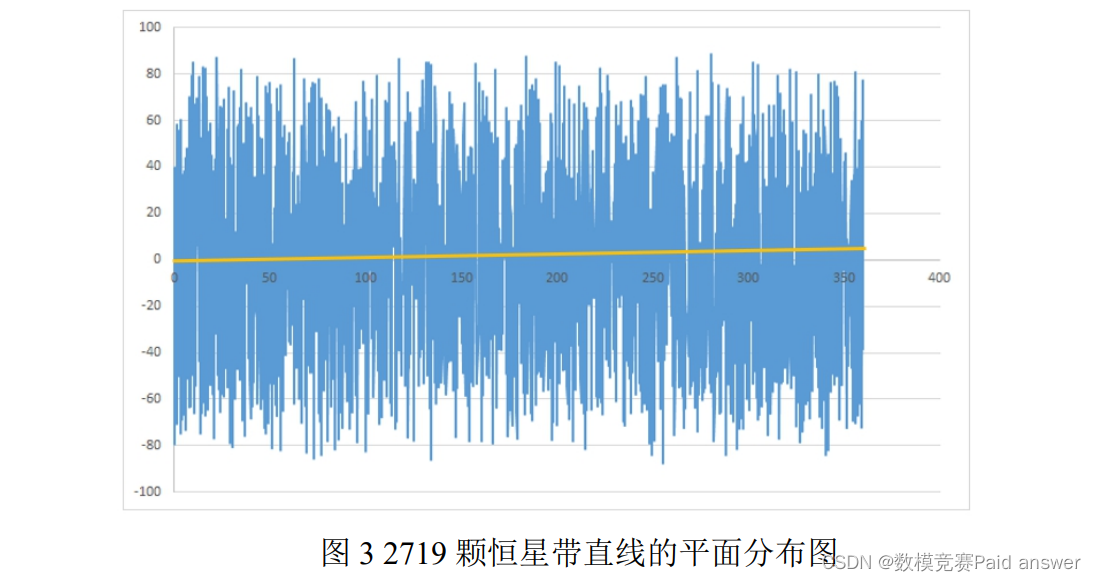
  通过图 3 可以看出恒星的平面分布较为均匀，仅有极个别的恒星散布在两侧，接下来对恒星自行的赤经分量和赤纬分量进行可视化，如图 4 所示

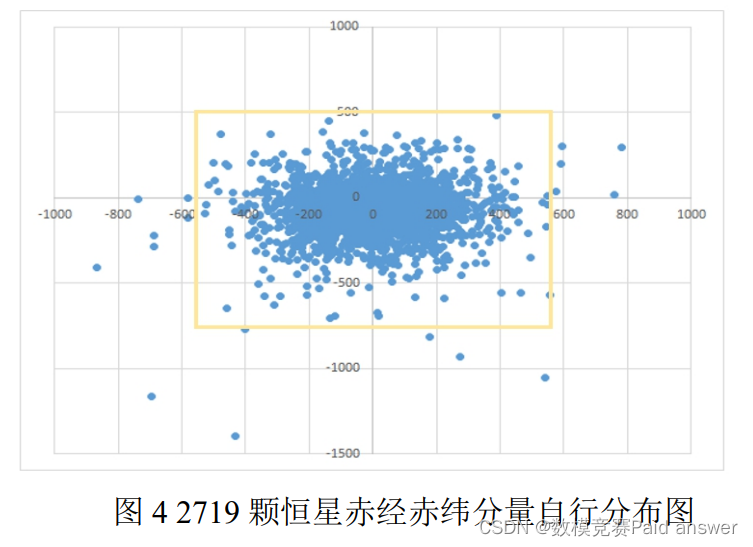
  由图 4 我们可以看出大多数恒星赤经赤纬自行分量较为紧凑，但仍有部分恒星自行分量散布在边缘，我们我们有必要将这类离群点剔除。接下来我们对 2719 颗恒星的RA、DE、pmRA 和pmDE这 4 个变量进行正态性分布检验，以便进行后续的离群点检测方法的选择，正态分布检验图如图 5 所示。

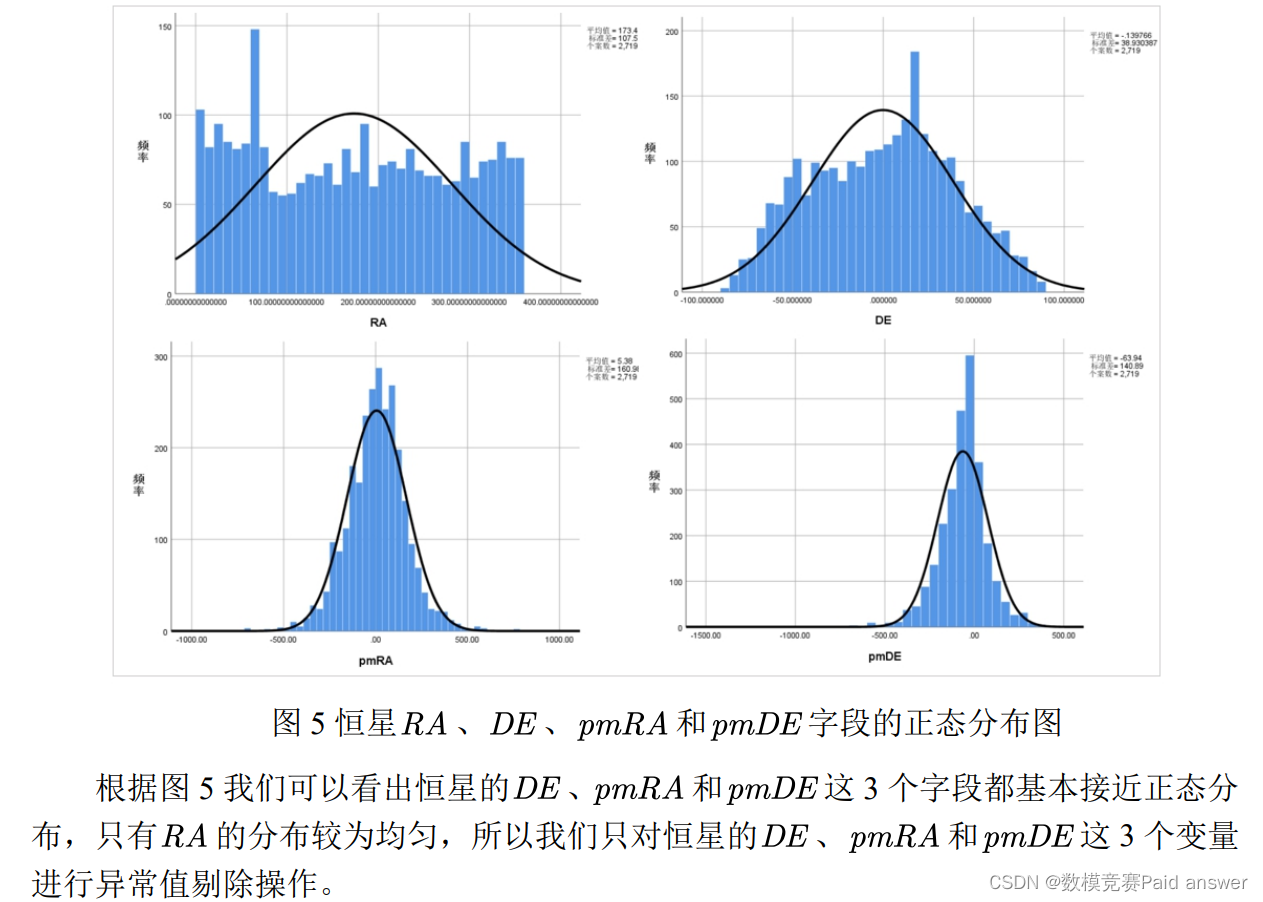
  异常值：指样本中的个别值，其数值明显偏离它们所属样本的其余观测值，也称离群值。遇到这一类问题常用的方法有：给定一个置信概率，并确定一个置信限，凡超过此限的误差，就认为它不属于随机误差范围，将其视为异常值剔除。对于本题我们采用拉依达准则法（3δ准则）：该方法简单，并且无需查表，是最常用的异常值判定与剔除准则。

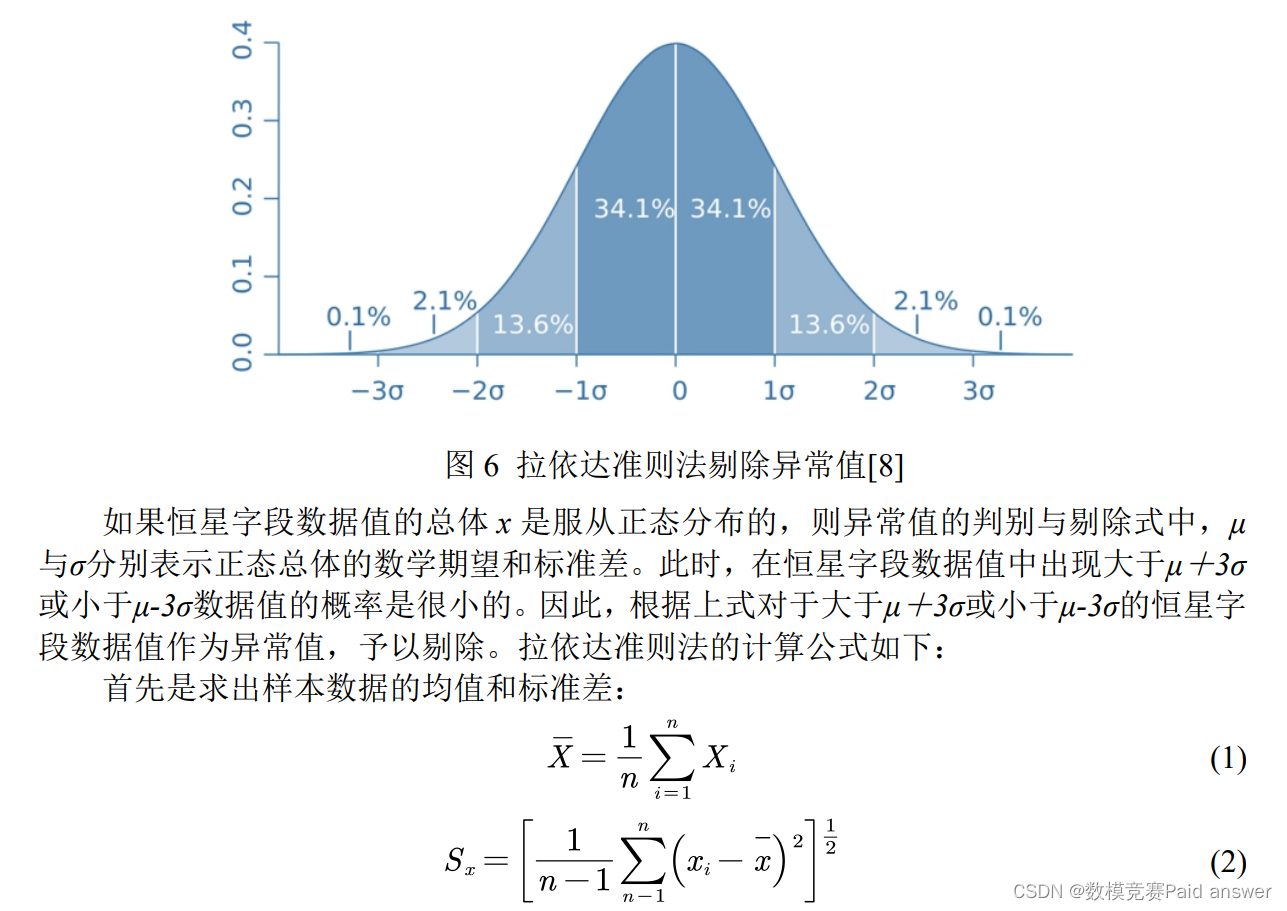
  由于附件中量化后的数据存在不同的量纲单位，因此数据的大小差别非常大，数据的范围也不相同。差异的较大会增大某些变量对毕星团成员星分类产生影响，同时会减弱某些变量对聚类模型的影响，所以需要对量化的数据进行归一化处理。将所有数据都转为[0,1]之间的数，可以消除数据因大小不一而造成的偏差。

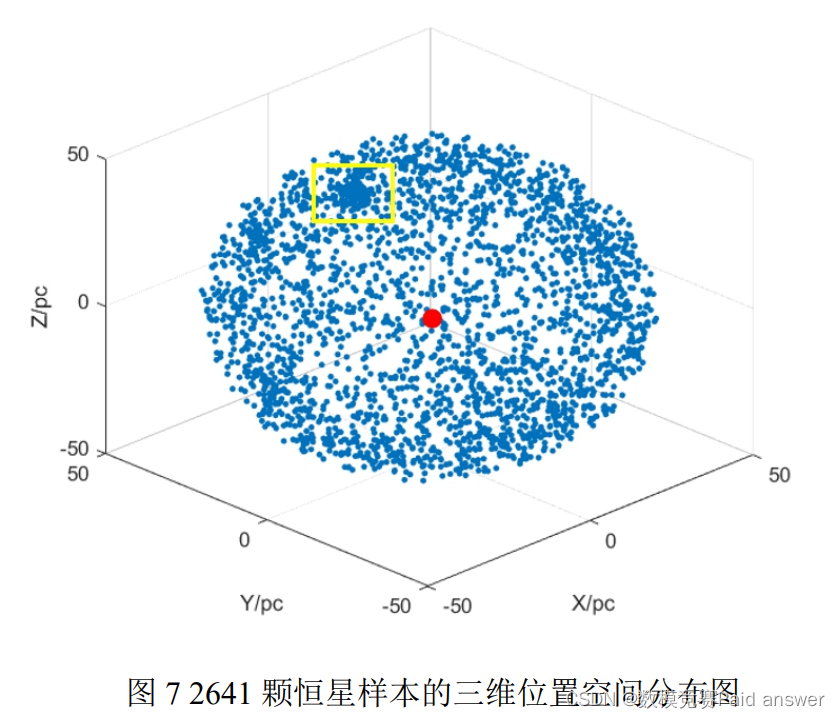
  根据图 7 我们可以明确发现，所有恒星汇集在一起后形成球状物。在球状物的左上角，由黄色方框标注的地方有大量的恒星团聚在一起，由于在宇宙中，星团与星团之间的距离是远大于星团内恒星的距离，而且星团内成员星有很多参数是区别于其他星团的，因此我们初步判定，该区域为毕星团区域。接下来我们开始建立基于改进 DBSCAN算法的 OPTICS 聚类模型。

  基于密度的聚类算法是数据挖掘技术中被广泛应用的一类算法，其核心思想是用一个点的 邻域内的邻居点数来衡量该点所在空间的密度。应用这种算法可以找出形状不规则的类，且在聚类前无需指定类的个数。



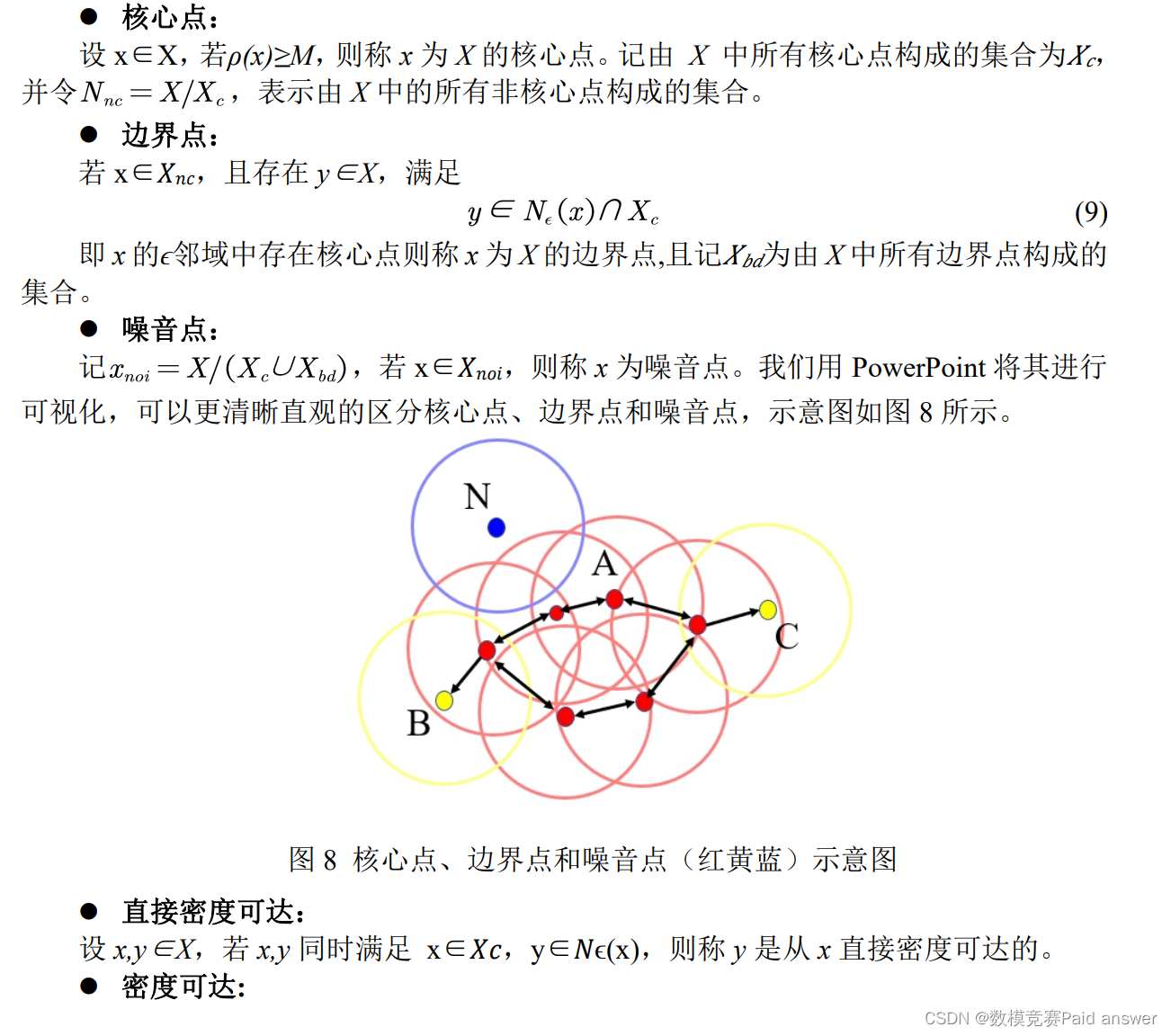
  （1）OPTICS 聚类模型的建立
  上文介绍的 DBSCAN 算法虽然具有速度快、能够处理噪声点、聚类簇的形状没有偏倚、无需设置聚类个数等种种优点，但是它的对于初始参数领域半径ϵ和阈值 M 的取值非常敏感。由于题目所给数据结构较为复杂，在使用 DBSCAN 算法时难以确定比较合适的参数。为克服 DBSCAN 算法的这一缺点，Ankerst Breunig 和 Kriegel 提出了OPTICS[10]算法，OPTICS 算法并不直接寻找各个簇, 而是将基于密度查找簇所需要的信息记录下来, 这些信息反映了数据空间基于密度的簇结构。同时, 从这些密度信息也可以直接发现各个簇。OPTICS 在 DBSCAN 算法的基础上引入了如下两个新的概念：

  （2）OPTICS 聚类模型的求解
  我们利用 Matlab 对上述模型进行求解，进而可以得到筛选出来的 331 颗毕星团成员星，具体成员详见附件。成员星三维位置空间中的分布图如图 9 所示

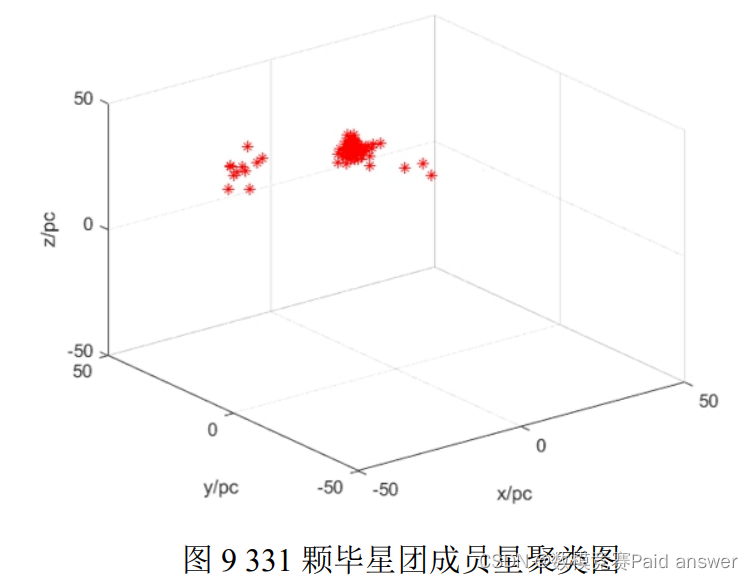
  根据图 9 我们可以发现，毕星团成员星团聚的位置与图 7 我们初步判定的区域大致相同，这可以证明我们得到的毕星团成员星较为准确。为了能进一步检验我们所构建的成员星聚类模型的精度，我们接下来开始建立毕星团成员星的检验模型。

  赫罗图是指恒星的光谱类型与光度之关系图。赫罗图的纵轴是光度与绝对星等，而横轴则是光谱类型及恒星的表面温度，从左向右递减。恒星的光谱型通常可大致分为O.B.A.F.G.K.M 七种[11,12]。由于视星等和光度的对数成正比，恒星的色指数附件数据已经给出，所以我们只需要计算出绝对星等即可绘制毕星团的赫罗图。
  （1）计算绝对星等

  （2）绘制赫罗图
  在上面我们求出了毕星团所有成员的绝对星等，我们将其作为赫罗图的纵坐标，然后将附件数据中的色指数变换成赫罗图的横坐标，使用 Matlab 初步绘制出毕星团的赫罗图，如图 10 所示。

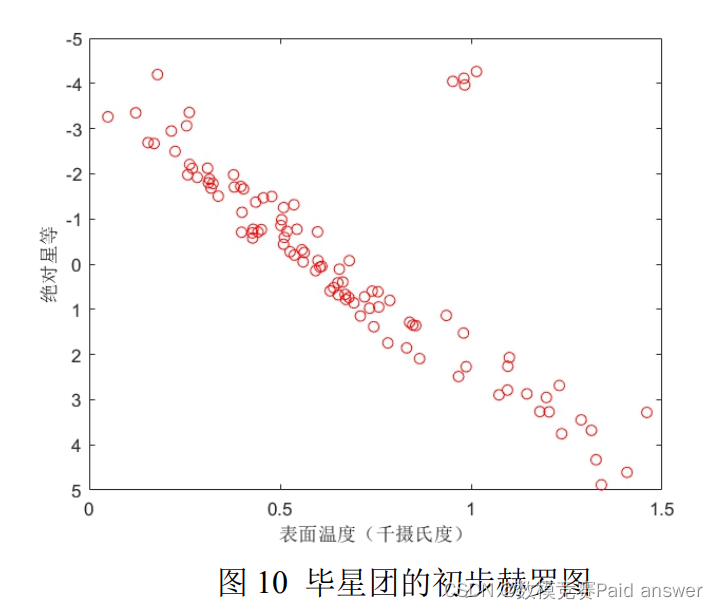
  绘制出毕星团的初步赫罗图后，我们再次使用 PowerPoint 对上图进行美化，并在坐标轴上添加了可见光度和光谱类型，得到最终的赫罗图如图 10 所示。

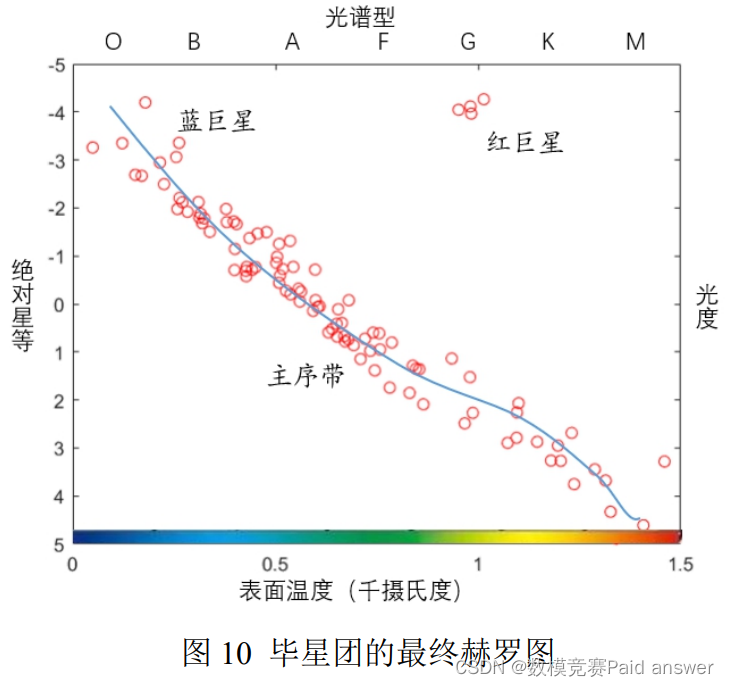
论文缩略图：

程序代码：

绘制恒星三维空间分布图 Matlab 代码

1. a=xlsread('C:\Users\Desktop\111.xlsx','sheet1');
2. x1=a(:,1);
3. y1=a(:,2);
4. z1=a(:,3);
5. c=[x1 y1 z1]
6. s=10;%É¢µã´óС
7. scatter3(x1,y1,z1,s,'filled');%c/2719,'filled');
8. title('2719¿ÅºãÐÇÈýά¿Õ¼ä·Ö²¼Í¼');
9. xlabel('X/pc');
10. ylabel('Y/pc');
11. zlabel('Z/pc');
1
2
3
4
5
6
7
8
9
10
11

聚类模型 Matlab 代码

12. % clc,clear
13. %% 由 Djl，Dfx，RA，DE 进行聚类
14. Djl= sqrt(pmRA.^2+pmDE.^2);
15. % 计算恒星自行距离
16. Dfx= atan(DE./RA);
17. % 计算恒星自行方向
18. p1=(Djl-min(Djl))/(max(Djl)-min(Djl))*(1-0)+0;
19. p2=(Dfx-min(Dfx))/(max(Dfx)-min(Dfx))*(1-(-1))+(-1);
20. p3=(RA-min(RA))/(max(RA)-min(RA))*(1-0)+0;
21. p4=(DE-min(DE))/(max(DE)-min(DE))*(1-(-1))+(-1);
22. %对用于聚类的数据进行标准化
23. X= [p1,p2,p3,p4];
24. Y = pdist(X,'seuclidean'); %使用标准欧氏距离
25. Z = linkage(Y,'single');% 使用最短距离法
26. %figure(2)
27. [~,~,OUTPERM]=dendrogram(Z,0); %% 绘制恒星一览图
28. %计算出秒差距 Parsec
29. Parsec=1000./Plx;
30. x=Parsec.*cos(DE/180*pi).*cos(RA/180*pi);
31. y=Parsec.*cos(DE/180*pi).*sin(RA/180*pi);
32. z=Parsec.*sin(DE/180*pi);
33. n=100;
34. Hyades_Num=OUTPERM(1:n);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可