- 1HarmonyOS 开发知识:一个基于 emitter 封装了一个便捷的 EventBus 事件通知_emitter的eventbus
- 2Day6 | Java框架 | Spring
- 3资深猎头解密:什么样的简历一投就中?_猎头提供简历爬虫
- 4TOMCAT PUT方法任意写文件(CVE-2017-12615)-靶场复现
- 5计算几何叉乘作用_叉乘的作用
- 6mysql之多表查询知识归纳总结_mysql查询多张表之间的数据关系
- 7docker容器启动rabbitmq_docker启动rabbitmq
- 8机器学习集成学习——Adaboost分离器算法_adaboost回归(adaboost.r)是一种集成学习算法,旨在提高回归算法的准确性。它通过
- 9薪资17K,在字节外包工作是一种什么体验..._字节外包测试工资多少
- 10idea不显示Git图标及相关操作按钮的解决办法_idea显示git图表
【NLP基础知识四】文本分类_nlp实战文本分类
赞
踩
如果你是NLP领域初学者,欢迎关注我的博客,我不仅会分享理论知识,更会通过实例和实用技巧帮助你迅速入门。我的目标是让每个初学者都能轻松理解复杂的NLP概念,并在实践中掌握这一领域的核心技能。
通过我的博客,你将了解到:
- NLP的基础概念,为你打下坚实的学科基础。
- 实际项目中的应用案例,让你更好地理解NLP技术在现实生活中的应用。
- 学习和成长的资源,助你在NLP领域迅速提升自己。
不论你是刚刚踏入NLP的大门,还是这个领域的资深专家,我的博客都将为你提供有益的信息。一起探索语言的边界,迎接未知的挑战,让我们共同在NLP的海洋中畅游!期待与你一同成长,感谢你的关注和支持。欢迎任何人前来讨论问题。
【NLP 基础知识一】词嵌入(Word Embeddings)
【NLP 基础知识二】词嵌入(Word Embeddings)之“Word2Vec:一种基于预测的方法”
【NLP 基础知识三】词嵌入(Word Embeddings)之“GloVe:单词表示的全局向量”
一、文本分类
文本分类是一个非常流行的任务。我们每天都会遇到它的应用,即邮件代理中的文本分类器:它对邮件进行分类并过滤垃圾邮件。其他常见应用还包括:文档分类、审查分类等。

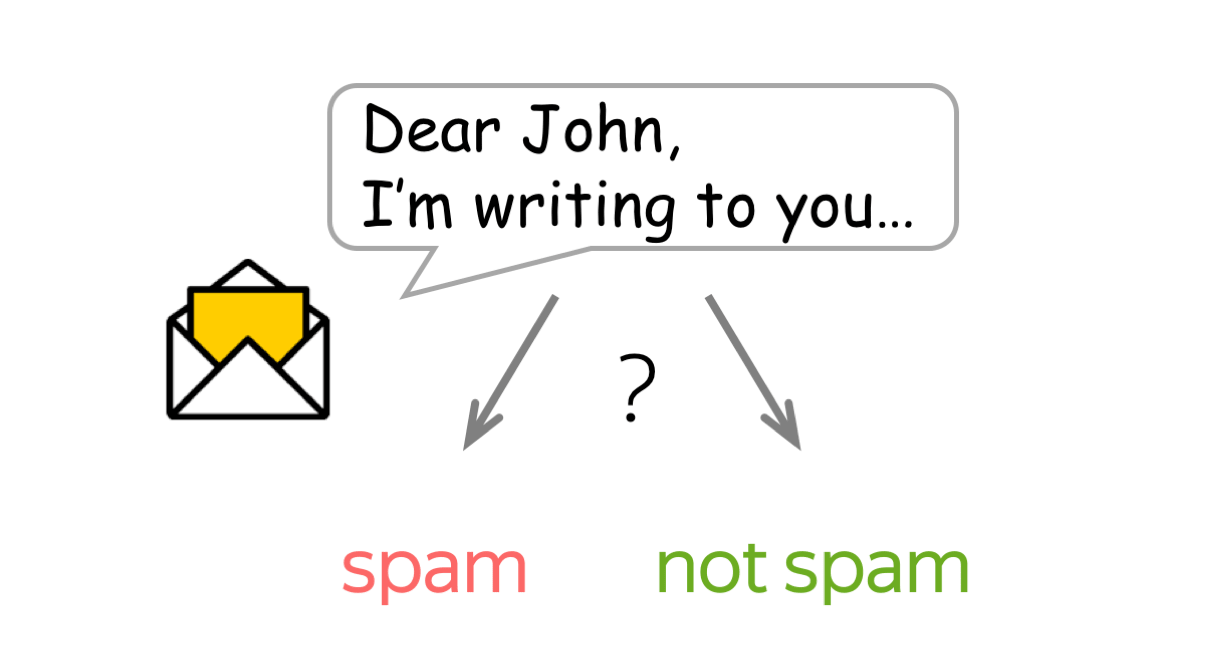

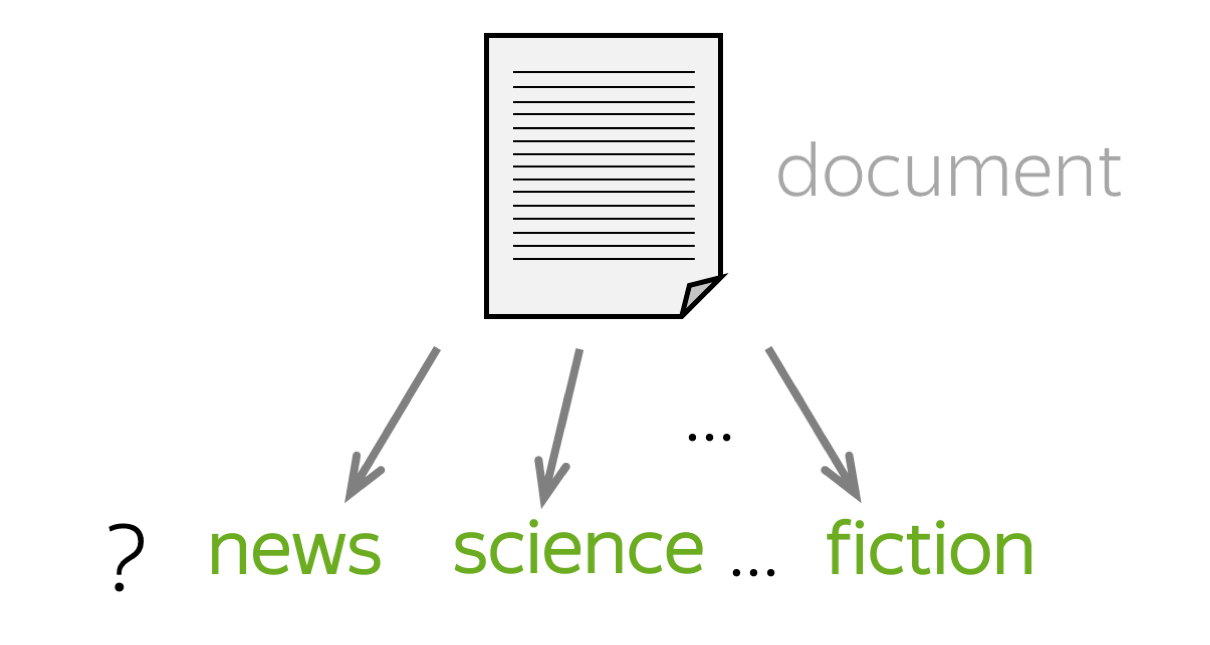
文本分类器常常不是作为一个单独的任务使用,而是作为更大的工作流管道的一部分。例如,一个语音助手对你的话语进行分类,以了解你想要什么(例如,设置闹钟、订购出租车或只是聊天),并根据分类器的决定将你的信息传递给不同的模型。另一个例子是网络搜索引擎:它可以使用分类器来识别查询语言,预测你的查询类型(例如,信息性、导航性、交易性),了解你除了要看文件之外,是否还要看图片或视频,等等。
由于大多数分类数据集都假定只有一个正确类别,所以,下面这章中我们重点介绍这种分类,即单标签分类。我们会在另一个章节中详细阐述 (多标签分类).
1、分类数据集
文本分类的数据集在大小(包括数据集大小和例子大小)、分类内容和标签数量方面都有很大不同。请看下面的统计数据。
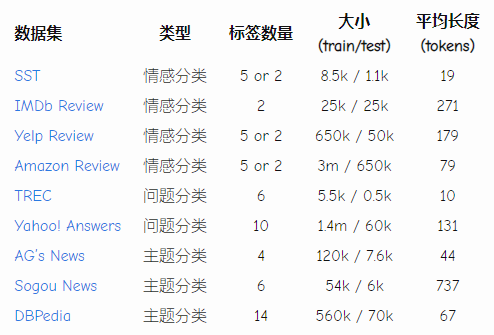
一些数据集可以从这里下载。
最流行的数据集是情感分类数据集。它们涉及对电影、地方或餐馆以及产品的评论。也有用于问题类型分类和主题分类的数据集。
####常用数据集介绍:
SST:
SST 是一个情感分类数据集,由电影评论(来自烂番茄 html 文件)组成。 数据集由句子的解析树组成,不仅是整个句子,而且更小的短语都有一个情感标签。
有五个标签:1(非常负面)、2(负面)、3(中性)、4(正面)和 5(非常正面)(标签有时候也可以表示为0-4)。 根据使用的标签不同,可以获得二分类的 SST-2 数据集(如果只考虑正面和负面)或细粒度的情绪分类 SST-5(使用所有标签)。
请注意,上面提到的数据集大小(train/dev/test 为 8.5k/2.2k/1.1k)是按照句子数量计算的。并且,使用了 215,154 个短语组成数据集中的每个句子。
IMDb Review:
IMDb 是来自 Internet 电影数据库的非正式电影评论的大型数据集。 该数据集中每部电影有不超过 30 条评论。 该数据集包含偶数个正面和负面评论,因此随机猜测产生 50% 的准确率。 评论高度两极分化:它们只有负面(最高分 4 分,满分 10)或正面(最低分 7 分,满分 10)。
Yelp Review:
Yelp 评论数据集来自 2015 年的 Yelp 数据集挑战赛 。根据标签的数量, Yelp Full(包含所有的 5 个标签)或 Yelp Polarity (仅含有正面和负面类别)。 Full在每个标签中有 130,000 个训练样本和 10,000 个测试样本, Polarity在每个类中有 280,000 个训练样本和 19,000 个测试样本。
Amazon Review:
亚马逊评论数据集由来自亚马逊的评论组成,其中包括产品和用户信息、评级和纯文本评论。 数据集来自 斯坦福网络分析项目 (SNAP)。 根据标签的数量,您可以获得 Amazon Full (包含所有的 5 个标签)或 Amazon Polarity(仅有正类和负类)。 Full在每个标签中有 600,000 个训练样本和 130,000 个测试样本, Polarity 在每个类中有 1800,000 个训练样本和 200,000 个测试样本。 使用的字段是评论标题和评论内容。
TREC:
TREC 是一个用于对自由事实问题进行分类的数据集。 它定义了一个两层分类法,表示 TREC 任务中典型答案的自然语义分类。 层次结构包含 6 个粗分类 (ABBREVIATION, ENTITY, DESCRIPTION, HUMAN, LOCATION and NUMERIC VALUE) 和 50 个细分类。
Yahoo! Answers:
数据集来自 Yahoo! Answers Comprehensive questions and Answers version 1.0 数据集 。 其中包含 10 个最大的主要类别: “Society & Culture”, “Science & Mathematics”, "Health, “Education & Reference”, “Computers & Internet”, “Sports”, “Business & Finance”, “Entertainment & Music”, “Family & Relationships”, “Politics & Government”. 每个类包含 140,000 个训练样本和 5,000 个测试样本。数据由问题标题和内容以及最佳答案组成。
AG’s News:
AG 的语料库是从 网络上的新闻文章 中获得的。 从这些文章中可以发现,只有 AG 的语料库仅包含 4 个最大类的标题和描述字段。
Sogou News:
搜狗新闻语料库是 SogouCA和SogouCS新闻语料库 由组合得到的。 该数据集由标记为 5 个类别的新闻文章(标题和内容字段)组成: “sports”, “finance”, “entertainment”, “automobile” and “technology”.
原始数据集是中文的,但您可以生成拼音 - 中文的拼音罗马字。 您可以使用 pypinyin 包结合 jieba 中文分词系统来完成(这是 介绍数据集的论文 所做的,这也是我在示例中向您展示的内容)。 然后可以将英语模型应用于此数据集而无需更改。
DBPedia:
DBpedia 是一个众包社区,旨在从维基百科中提取结构化信息。 DBpedia 本体分类数据集是通过从 DBpedia 2014中挑选 14 个不重叠的类构建的。每一个类中包含 40,000 个随机选择的训练样本和 5,000 个测试样本。 因此,训练数据集的总大小为 560,000,测试数据集大小为 70,000。
2、通用视角
这里我们提供了一个关于分类的通用视角,并介绍了相关符号的形式化定义。该通用视角同时适用于经典方法和基于神经网络方法。
我们假设有一个带真实标签的文档集合。分类器的输入是带有token序列
(
x
1
,
…
,
x
n
)
(x_1, \dots, x_n)
(x1,…,xn)的文档
x
=
(
x
1
,
…
,
x
n
)
x=(x_1, \dots, x_n)
x=(x1,…,xn) ,输出是标签
y
∈
1
…
k
y\in 1\dots k
y∈1…k。 通常情况下,分类器估计的是类别的概率分布,我们希望正确类别的概率是最高的。
获得特征表示及分类
文本分类拥有以下结构:
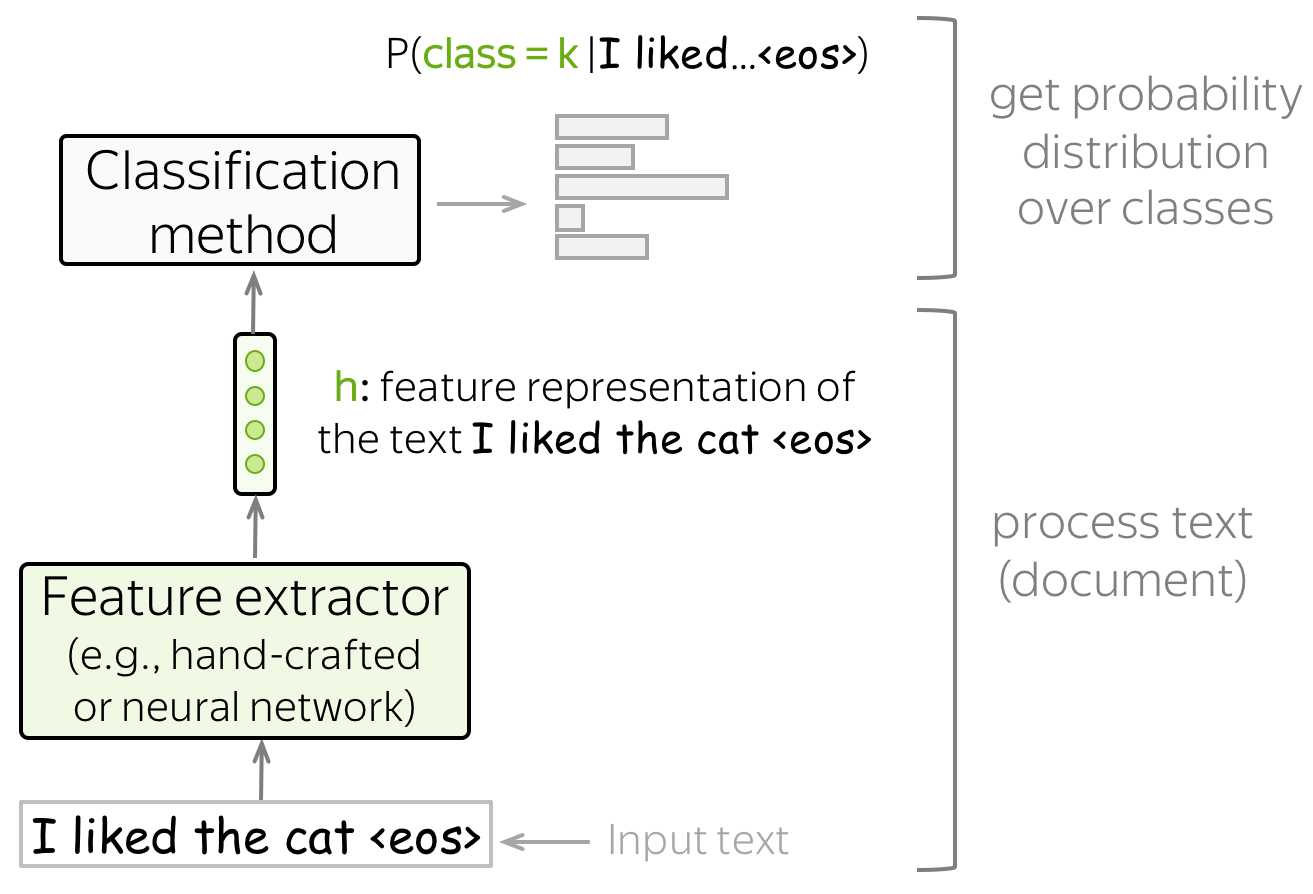
- 特征提取器
特征提取器可以手动设计 (如经典方法)或通过”学习”获得(如神经网络). - 分类器
一个分类器必须在给定文本的特征表示时分配类别概率。最常见的方法是使用 逻辑回归,但其他变体也是可能的(例如,朴素贝叶斯分类器或 SVM)。
在本文中,我们将主要研究建立文本特征表示的不同方法,并使用这种表示来获得类别概率。
生成模型与判别模型
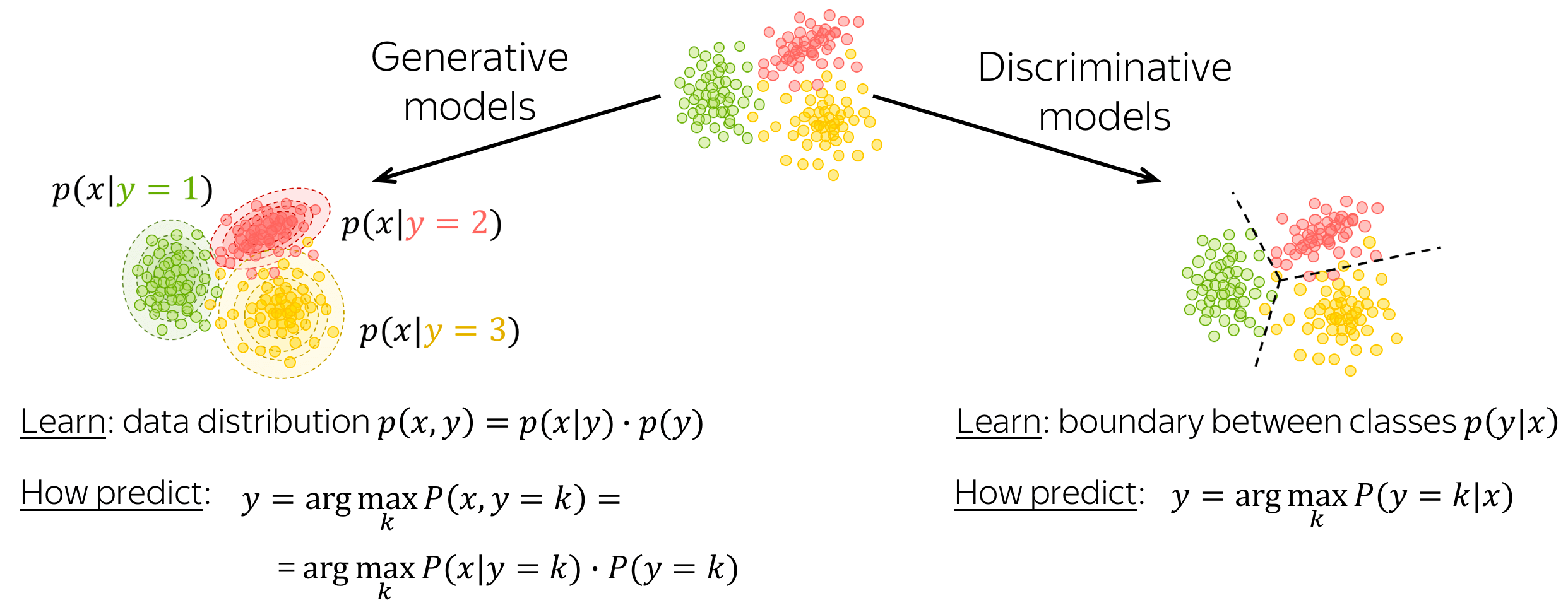
一个分类模型可以是生成式的,也可以是判别式的。
- 生成模型
生成模型学习数据的联合概率分布 p ( x , y ) = p ( x ∣ y ) ⋅ p ( y ) p(x, y) = p(x|y)\cdot p(y) p(x,y)=p(x∣y)⋅p(y)。为了对输入 x x x 进行预测,这些模型选择一个具有最高联合概率的类别:
y = arg max k p ( x ∣ y = k ) ⋅ p ( y = k ) y=\arg\max_k p(x|y=k)\cdot p(y=k) y=argkmaxp(x∣y=k)⋅p(y=k) - 判别模型
判别模型只关注条件概率 p ( y ∣ x ) p(y|x) p(y∣x),即,只需学习类别之间的边界。为了对输入 x x x进行预测,这些模型选择一个具有最高条件概率的类别:
y = arg max k p ( y = k ∣ x ) y = \arg \max\limits_{k}p(y=k|x) y=argkmaxp(y=k∣x)
本文中,这两类模型都会出现。
3、文本分类经典方法
本章我们讨论经典的文本分类方法。它们在神经网络开始流行之前就已经被开发出来了,对于小型数据集来说,其性能仍可与基于神经网络的模型相媲美。
编者按: 在课程的后面,我们将学习迁移学习,可以使神经网络方法即使对于非常小的数据集也有更好的表现。但让我们一步一步来:目前,经典方法是你的模型的一个很好的基线。
朴素贝叶斯分类器
下面给出了朴素贝叶斯方法的总体想法:我们用贝叶斯规则重写条件类概率
P
(
y
=
k
∣
x
)
P(y=k|x)
P(y=k∣x),得到
P
(
x
∣
y
=
k
)
⋅
P
(
y
=
k
)
P(x|y=k)\cdot P(y=k)
P(x∣y=k)⋅P(y=k)。
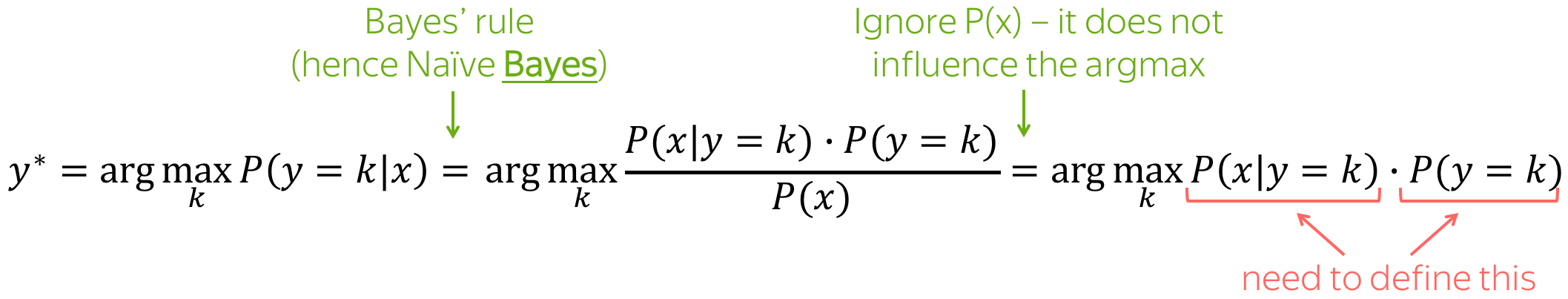
这是一个生成模型!
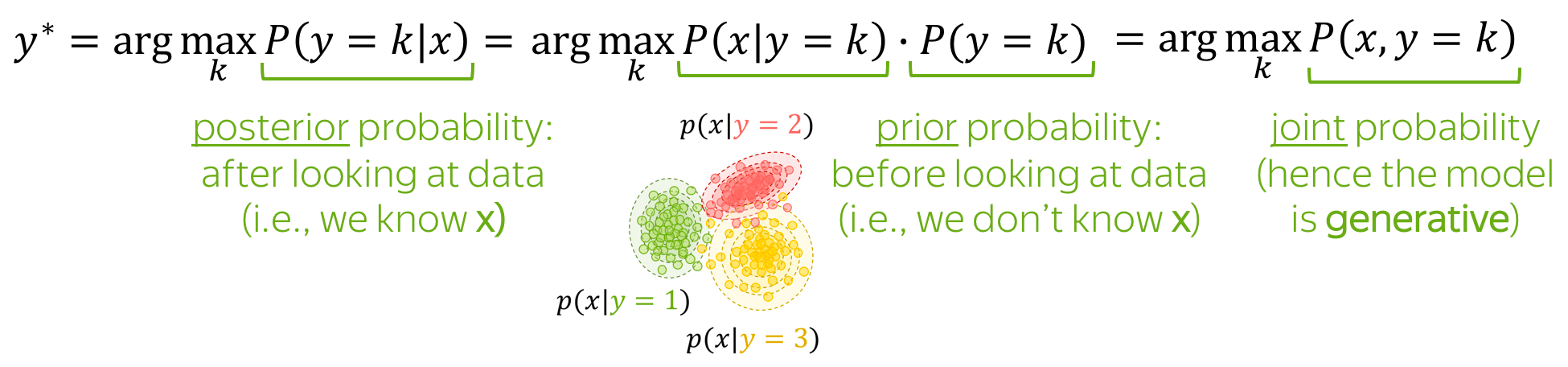
朴素贝叶斯是一个生成模型:它对数据的联合概率进行建模。
同时,要注意术语:
- 先验概率 P ( y = k ) P(y=k) P(y=k):看数据前的类概率(即在知道x之前);
- 后验概率 P ( y = k ∣ x ) P(y=k|x) P(y=k∣x):看完数据后的类别概率(即知道具体的 x x x后);
- 联合概率 P ( x , y ) P(x, y) P(x,y): :数据的联合概率(即例子 x x x和标签 y y y);
- 最大后验(MAP)估计:我们选择具有最高后验概率的类别。
如何定义 P ( x ∣ y = k ) P(x|y=k) P(x∣y=k) 和 P ( y = k ) P(y=k) P(y=k)?
P
(
y
=
k
)
P(y=k)
P(y=k):标签计数
P
(
y
=
k
)
P(y=k)
P(y=k) 很容易得到:我们只需计算具有标签
k
k
k的文档的比例(即最大似然估计,MLE)。也就是说,
P
(
y
=
k
)
=
N
(
y
=
k
)
∑
i
N
(
y
=
i
)
,
P(y=k)=\frac{N(y=k)}{\sum\limits_{i}N(y=i)},
P(y=k)=i∑N(y=i)N(y=k),
其中,
N
(
y
=
k
)
N(y=k)
N(y=k) 是标签为
k
k
k 的例子(文档)的数量。
P
(
x
∣
y
=
k
)
P(x|y=k)
P(x∣y=k):先使用 “朴素” 假设,然而计数
这里,我们假设文档
X
X
X 被表示为一组特征,例如,它的一组词
(
x
1
,
…
,
x
n
)
(x_1, \dots, x_n)
(x1,…,xn):
P
(
x
∣
y
=
k
)
=
P
(
x
1
,
…
,
x
n
∣
y
=
k
)
.
P(x| y=k)=P(x_1, \dots, x_n|y=k).
P(x∣y=k)=P(x1,…,xn∣y=k).
朴素贝叶斯假设为
- 词袋假设:词的顺序并不重要,
- 条件独立性假设:特征(词)在不同类别间是独立的。
直观地说,我们假设每个词出现在类别为k的文件中的概率不取决于上下文(既不取决于词序,也不取决于其他词)。例如,我们可以说, awesome, brilliant, great更有可能出现在有积极情绪的文件中,而 awful, boring, bad 更有可能出现在消极文件中,但我们并不知道这些(或其他)词之间如何相互影响。
通过这些“朴素” 假设,我们可以得到:
P
(
x
∣
y
=
k
)
=
P
(
x
1
,
…
,
x
n
∣
y
=
k
)
=
∏
t
=
1
n
P
(
x
t
∣
y
=
k
)
.
P(x| y=k)=P(x_1, \dots, x_n|y=k)=\prod\limits_{t=1}^nP(x_t|y=k).
P(x∣y=k)=P(x1,…,xn∣y=k)=t=1∏nP(xt∣y=k).
概率
P
(
x
i
∣
y
=
k
)
P(x_i|y=k)
P(xi∣y=k) 被估计为单词
x
i
x_i
xi 出现在第
k
k
k 类的文档中的次数占所有token出现在k类文档次数比例,即:
P
(
x
i
∣
y
=
k
)
=
N
(
x
i
,
y
=
k
)
∑
t
=
1
∣
V
∣
N
(
x
t
,
y
=
k
)
,
P(x_i|y=k)=\frac{N(x_i, y=k)}{\sum\limits_{t=1}^{|V|}N(x_t, y=k)},
P(xi∣y=k)=t=1∑∣V∣N(xt,y=k)N(xi,y=k),
其中,
N
(
x
i
,
y
=
k
)
N(x_i, y=k)
N(xi,y=k) 是token
x
i
x_i
xi 出现在类别为
k
k
k 的文件中的次数,
V
V
V 是词汇表(更一般地说,所有可能特征组成的集合)。
如果 N ( x i , y = k ) = 0 N(x_i, y=k)=0 N(xi,y=k)=0 怎么办?需要避免这种情况!
如果
N
(
x
i
,
y
=
k
)
=
0
N(x_i, y=k)=0
N(xi,y=k)=0,即在训练中我们没有在类别
k
k
k 的文档中看到token
x
i
x_i
xi 怎么办?这将使整个文档的概率归零,而这不是我们想要的!例如,如果我们在训练中没有看到一些罕见的词(例如,pterodactyl 或 abracadabra),这并不意味着一个文件永远不可能包含这些词。

为避免这种情况,我们使用了一个小trick:我们在所有单词的计数中添加一个小的
δ
\delta
δ:
P
(
x
i
∣
y
=
k
)
=
δ
+
N
(
x
i
,
y
=
k
)
∑
t
=
1
∣
V
∣
(
δ
+
N
(
x
t
,
y
=
k
)
)
=
δ
+
N
(
x
i
,
y
=
k
)
δ
⋅
∣
V
∣
+
∑
t
=
1
∣
V
∣
N
(
x
t
,
y
=
k
)
,
P(x_i|y=k)=\frac{\color{red}{\delta} +\color{black} N(x_i, y=k) }{\sum\limits_{t=1}^{|V|}(\color{red}{\delta} +\color{black}N(x_t, y=k))} = \frac{\color{red}{\delta} +\color{black} N(x_i, y=k) }{\color{red}{\delta\cdot |V|}\color{black} + \sum\limits_{t=1}^{|V|}\color{black}N(x_t, y=k)} ,
P(xi∣y=k)=t=1∑∣V∣(δ+N(xt,y=k))δ+N(xi,y=k)=δ⋅∣V∣+t=1∑∣V∣N(xt,y=k)δ+N(xi,y=k),
其中
δ
\delta
δ 可以使用交叉验证来选择。
注意:这是拉普拉斯平滑(如果
δ
=
1
\delta=1
δ=1,又称 Add-1平滑 )。 我们将在下一讲关于语言建模的文章中了解更多关于平滑的知识。
预测
正如我们已经提到的,朴素贝叶斯(以及更广泛的生成模型)根据数据和类别的联合概率进行预测:
y
∗
=
arg
max
k
P
(
x
,
y
=
k
)
=
arg
max
k
P
(
y
=
k
)
⋅
P
(
x
∣
y
=
k
)
.
y^{\ast} = \arg \max\limits_{k}P(x, y=k) = \arg \max\limits_{k} P(y=k)\cdot P(x|y=k).
y∗=argkmaxP(x,y=k)=argkmaxP(y=k)⋅P(x∣y=k).
直观地说,朴素贝叶斯期望一些词能作为类别标志。例如,在情感分类中, awesome, brilliant, great 等token将具有更高的概率,因为它们属于positive类别而不是negative类别。同样地, awful, boring, bad 这些token在给定negative类别的情况下会有更高的概率,而不是positive类别。

关于朴素贝叶斯的进一步说明
实践说明:用对数概率之和代替概率之积
朴素贝叶斯用于分类的主要表达式是概率的乘积:
P
(
x
,
y
=
k
)
=
P
(
y
=
k
)
⋅
P
(
x
1
,
…
,
x
n
∣
y
)
=
P
(
y
=
k
)
⋅
∏
t
=
1
n
P
(
x
t
∣
y
=
k
)
.
P(x, y=k)=P(y=k)\cdot P(x_1, \dots, x_n|y)=P(y=k)\cdot \prod\limits_{t=1}^nP(x_t|y=k).
P(x,y=k)=P(y=k)⋅P(x1,…,xn∣y)=P(y=k)⋅t=1∏nP(xt∣y=k).
许多概率的乘积在数值上可能非常不稳定(乘积导致溢出或浮点损失)。因此,通常我们考虑
log
P
(
x
,
y
)
\log P(x, y)
logP(x,y) 而不是
P
(
x
,
y
)
P(x, y)
P(x,y) :
log
P
(
x
,
y
=
k
)
=
log
P
(
y
=
k
)
+
∑
t
=
1
n
log
P
(
x
t
∣
y
=
k
)
.
\log P(x, y=k)=\log P(y=k) + \sum\limits_{t=1}^n\log P(x_t|y=k).
logP(x,y=k)=logP(y=k)+t=1∑nlogP(xt∣y=k).
由于我们只关心argmax,我们可以考虑
log
P
(
x
,
y
)
\log P(x, y)
logP(x,y) 而不是
P
(
x
,
y
)
P(x, y)
P(x,y).
重要! 请注意,在实践中,我们通常会处理对数概率而不是概率。
通用框架的视角
还记得我们关于分类任务的通用视角 吗?我们使用某种方法获得输入文本的特征表示,然后使用这种特征表示进行分类。
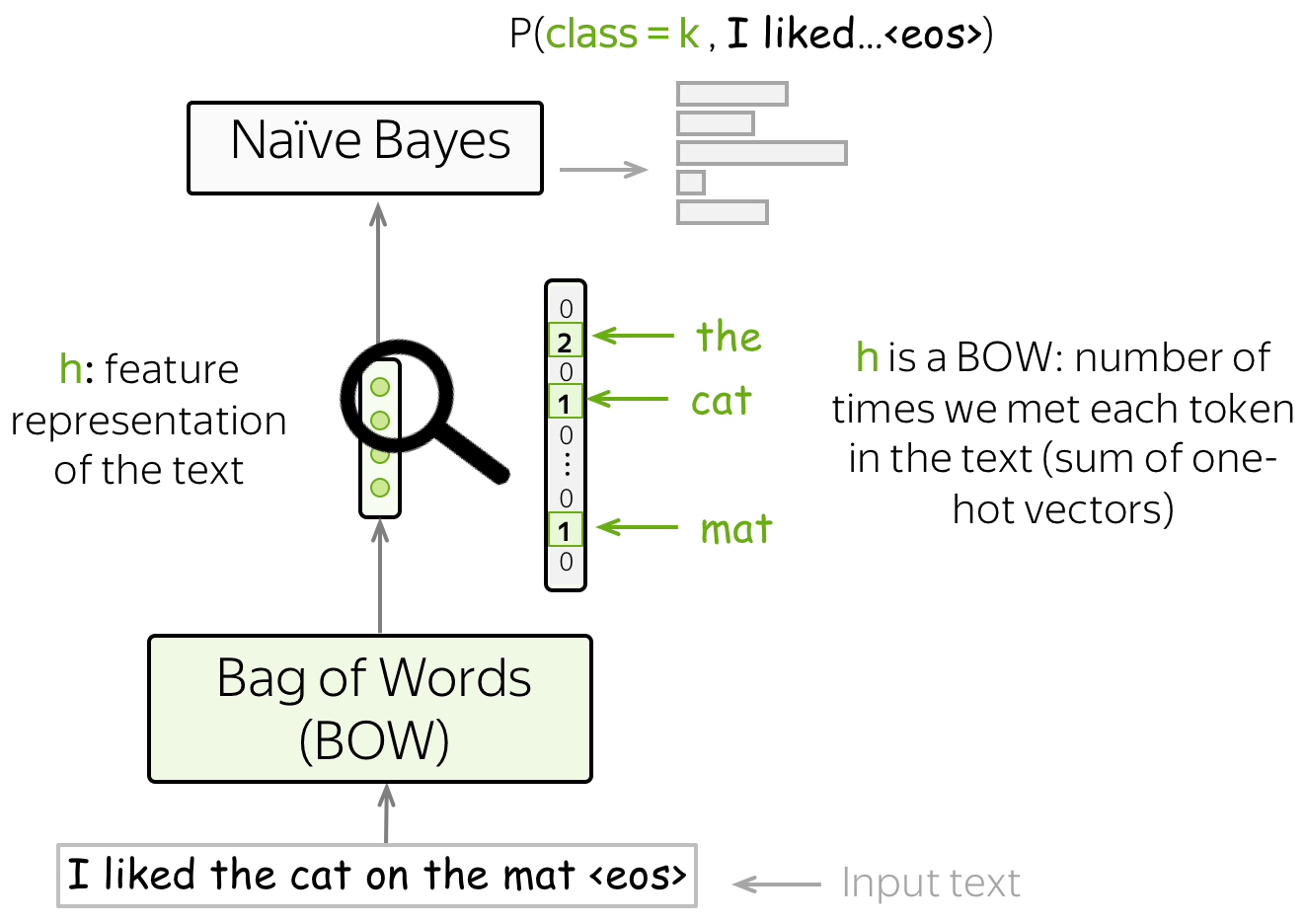
在朴素贝叶斯中,我们的特征是词,而特征表示是词袋(BOW)表示(是词的one-hot表示的总和)。事实上,为了评估
P
(
x
,
y
)
P(x, y)
P(x,y) ,我们只需要计算每个token在文本中出现的次数。
特征设计
在标准设置中,我们使用词作为特征。然而,你也可以使用其他类型的特征。URL,用户ID,等等。
最大熵分类器(又名逻辑回归)
与朴素贝叶斯不同,最大熵分类器是一个判别模型,也就是说,我们对概率
P
(
y
=
k
∣
x
)
P(y=k|x)
P(y=k∣x)感兴趣而不是联合分布
p
(
x
,
y
)
p(x, y)
p(x,y) 。 另外,我们将学习如何使用特征:这与朴素贝叶斯不同,在朴素贝叶斯中我们自己定义如何使用特征。
在这里,我们也必须手动定义特征,但我们有更多的发挥空间:特征不一定是分类相关的(在朴素贝叶斯中,它们必须是!)。我们可以使用BOW表示方法,或者想出一些更有趣的东西。
该方法中,一般分类pipeline是这样的:
- 得到 h = ( f 1 , f 2 , … , f n ) \color{#7aab00}{h}\color{black}=(\color{#7aab00}{f_1}\color{black}, \color{#7aab00}{f_2}\color{black}, \dots, \color{#7aab00}{f_n}\color{black}{)} h=(f1,f2,…,fn) - 输入文本的特征表示;
- 取 w ( i ) = ( w 1 ( i ) , … , w n ( i ) ) w^{(i)}=(w_1^{(i)}, \dots, w_n^{(i)}) w(i)=(w1(i),…,wn(i)) - 每个类别的特征权重的向量;
- 对于每一个类,对特征进行权衡,即取特征表示
h
\color{#7aab00}{h}
h 与特征权重
w
(
k
)
w^{(k)}
w(k)的点积:
w ( k ) h = w 1 ( k ) ⋅ f 1 + ⋯ + w n ( k ) ⋅ f n , k = 1 , … , K . w^{(k)}\color{#7aab00}{h}\color{black} = w_1^{(k)}\cdot\color{#7aab00}{f_1}\color{black}+\dots+ w_n^{(k)}\cdot\color{#7aab00}{f_n}\color{black}{, \ \ \ \ \ k=1, \dots, K.} w(k)h=w1(k)⋅f1+⋯+wn(k)⋅fn, k=1,…,K.
为了在上面的求和中得到一个偏差项,我们定义其中一个特征为1(例如, f 0 = 1 \color{#7aab00}{f_0}=1 f0=1)。那么
w ( k ) h = w 0 ( k ) + w 1 ( k ) ⋅ f 1 + ⋯ + w n ( k ) ⋅ f n , k = 1 , … , K . w^{(k)}\color{#7aab00}{h}\color{black} = \color{red}{w_0^{(k)}}\color{black} + w_1^{(k)}\cdot\color{#7aab00}{f_1}\color{black}+\dots+ w_n^{(k)}\cdot\color{#7aab00}{f_{n}}\color{black}{, \ \ \ \ \ k=1, \dots, K.} w(k)h=w0(k)+w1(k)⋅f1+⋯+wn(k)⋅fn, k=1,…,K. - 使用softmax得到类别概率:
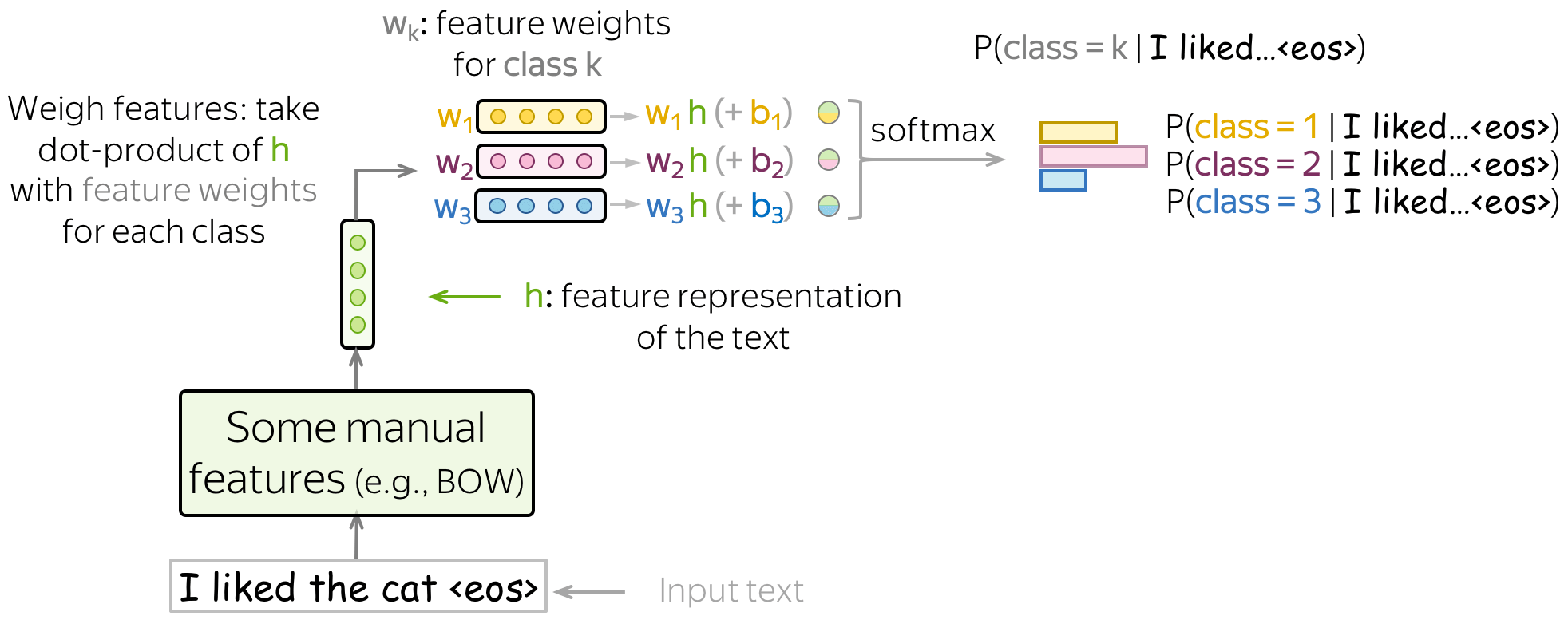
P ( c l a s s = k ∣ h ) = exp ( w ( k ) h ) ∑ i = 1 K exp ( w ( i ) h ) . P(class=k|\color{#7aab00}{h}\color{black})= \frac{\exp(w^{(k)}\color{#7aab00}{h}\color{black})}{\sum\limits_{i=1}^K \exp(w^{(i)}\color{#7aab00}{h}\color{black})}. P(class=k∣h)=i=1∑Kexp(w(i)h)exp(w(k)h).
将我们在上一步得到的 K K K 值归一到输出类别的概率分布。
请看下面的插图(类别用不同颜色表示)。
训练:最大似然估计
给定训练实例
x
1
,
…
,
x
N
x^1, \dots, x^N
x1,…,xN 与相应的标签
y
i
∈
{
1
,
…
,
K
}
y^i\in\{1, \dots, K\}
yi∈{1,…,K} ,我们选择权重
w
(
k
)
,
k
=
1..
K
w^{(k)}, k=1..K
w(k),k=1..K ,使训练数据的概率最大化:
w
∗
=
arg
max
w
∑
i
=
1
N
log
P
(
y
=
y
i
∣
x
i
)
.
w^{\ast}=\arg \max\limits_{w}\sum\limits_{i=1}^N\log P(y=y^i|x^i).
w∗=argwmaxi=1∑NlogP(y=yi∣xi).
换言之,我们选择合适的参数使得数据更容易 出现。因此,这被称为参数的最大似然估计(MLE) 。
为了找到使数据对数似然可能性最大化的参数,我们使用梯度上升法:在数据的多次迭代中逐渐修改权重。在每一步,我们都要最大化模型分配给正确类别的概率。
等价于最小化交叉熵
请注意,最大化数据对数似然相当于最小化目标概率分布
p
∗
=
(
0
,
…
,
0
,
1
,
0
,
…
)
p^{\ast} = (0, \dots, 0, 1, 0, \dots)
p∗=(0,…,0,1,0,…) (目标标签为1,其余为0)和模型分布
p
=
(
p
1
,
…
,
p
K
)
,
p
i
=
p
(
i
∣
x
)
p=(p_1, \dots, p_K), p_i=p(i|x)
p=(p1,…,pK),pi=p(i∣x)的交叉熵:
L
o
s
s
(
p
∗
,
p
)
=
−
p
∗
log
(
p
)
=
−
∑
i
=
1
K
p
i
∗
log
(
p
i
)
.
Loss(p^{\ast}, p^{})= - p^{\ast} \log(p) = -\sum\limits_{i=1}^{K}p_i^{\ast} \log(p_i).
Loss(p∗,p)=−p∗log(p)=−i=1∑Kpi∗log(pi).
因为仅有一个
p
i
∗
p_i^{\ast}
pi∗ 是非零的(1代表目标标签
k
k
k,0代表其余),我们将得到:
L
o
s
s
(
p
∗
,
p
)
=
−
log
(
p
k
)
=
−
log
(
p
(
k
∣
x
)
)
.
Loss(p^{\ast}, p) = -\log(p_{k})=-\log(p(k| x)).
Loss(p∗,p)=−log(pk)=−log(p(k∣x)).
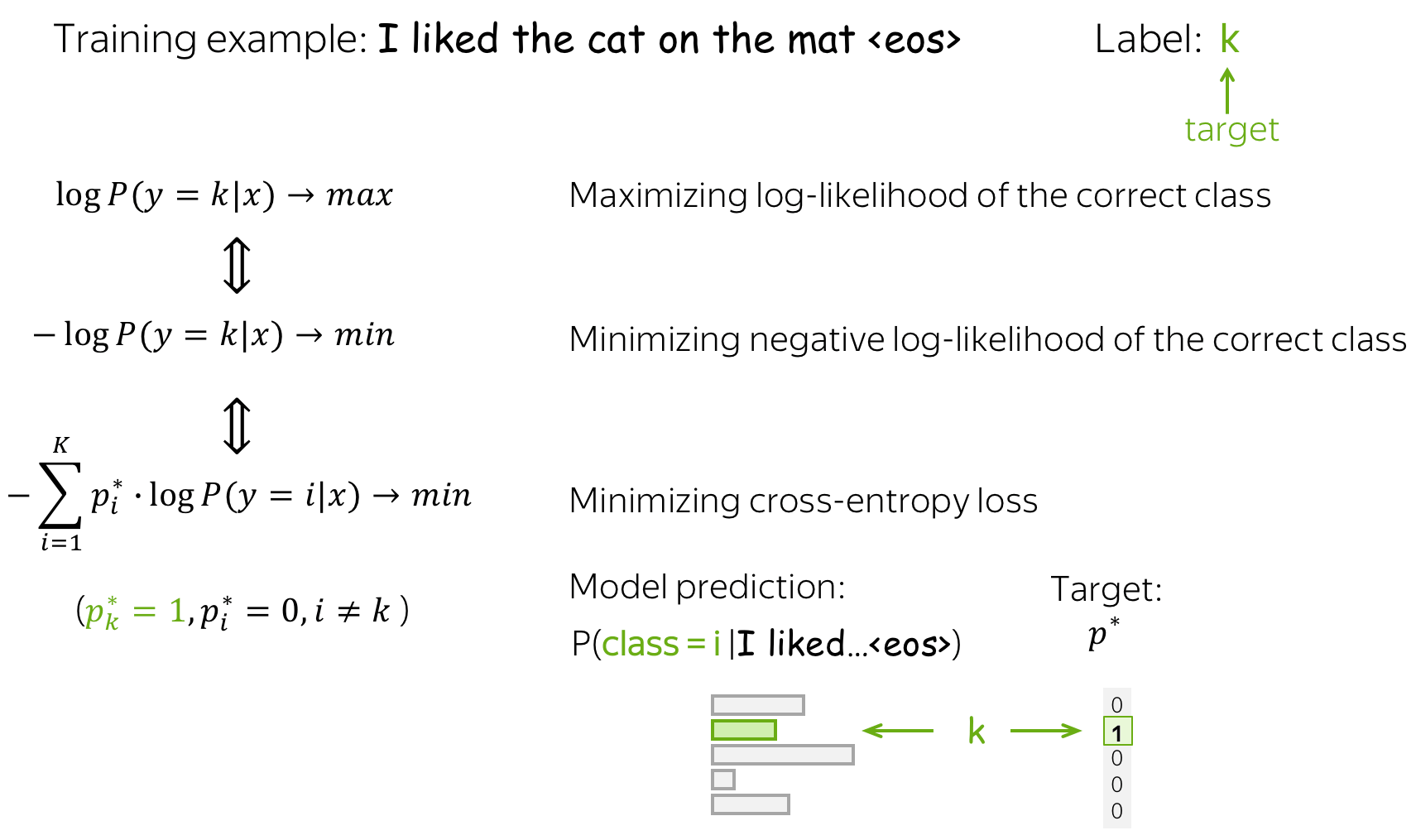
这种等价性对于你理解非常重要:在谈论神经方法时,人们通常会说他们最小化了交叉熵损失。 不要忘记这与最大化数据对数似然是等价的。
朴素贝叶斯与逻辑斯蒂回归

接下来我们讨论逻辑斯蒂回归和朴素贝叶斯的优缺点。
- 简单
两种方法都很简单;朴素贝叶斯是最简单的一种。 - 可解释性
这两种方法都是可解释的:你可以查看对预测影响最大的特征(在朴素贝叶斯中,通常是单词,在逻辑斯蒂回归中 - 无论你定义什么)。 - 训练速度
朴素贝叶斯的训练速度非常快——它只需要一次遍历训练数据来统计计数。对于逻辑斯蒂回归,情况并非如此:你必须多次遍历数据,直到梯度上升收敛。 - 独立性假设
朴素贝叶斯太“朴素”了,它假设在给定类别的情况下特征(词)是条件独立的。逻辑斯蒂回归没有做出这个假设,我们可以希望它更好。 - 文本表示:手动定义
两种方法都使用手动定义的特征表示(在朴素贝叶斯中,BOW 是标准选择,但仍然可以自己选择)。虽然手动定义的特性有利于可解释性,但它们可能对性能没有那么好,你可能会错过一些对任务有用的东西。
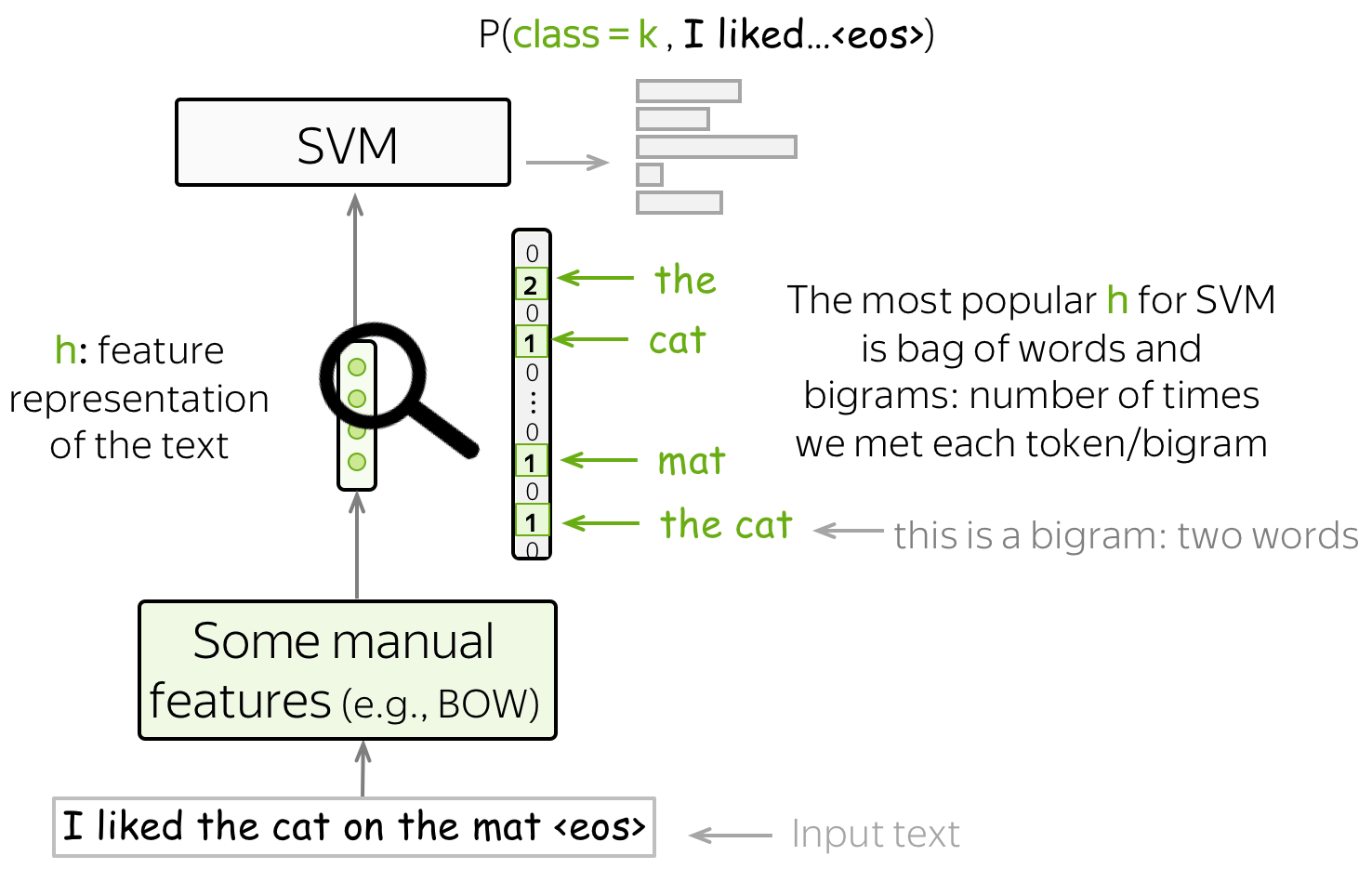
SVM 文本分类器
另一种基于手动设计特征的文本分类方法是 SVM。 SVM 最基本(也是最流行的)功能是词袋 (bag-of-words) 和 ngram 袋 (bag-of-ngrams) (ngram 是 n 个词的元组)。 凭借这些简单的特征,具有线性核的 SVM 比朴素贝叶斯表现更好(例如,参见论文 使用支持向量机的问题分类)。
4、神经网络文本分类
今天太晚了,先到这里,Word2Vec:一种基于预测的方法,这一章篇幅有点多,明天才能产出。
出了链接就在这里:
在这个充满科技魔力的时代,自然语言处理(NLP)正如一颗璀璨的明星般照亮我们的数字世界。当我们涉足NLP的浩瀚宇宙,仿佛开启了一场语言的奇幻冒险。正如亚历克斯·康普顿所言:“语言是我们思想的工具,而NLP则是赋予语言新生命的魔法。”这篇博客将引领你走进NLP前沿,发现语言与技术的交汇点,探寻其中的无尽可能。不论你是刚刚踏入NLP的大门,还是这个领域的资深专家,我的博客都将为你提供有益的信息。一起探索语言的边界,迎接未知的挑战,让我们共同在NLP的海洋中畅游!期待与你一同成长,感谢你的关注和支持。欢迎任何人前来讨论问题。



