DP是动态规划（Dynamic Programming）的缩写，是一种解决复杂问题的算法设计技术。动态规划通常用于优化问题，通过将问题分解为子问题并使用子问题的解来构建整体解决方案。
动态规划算法的核心思想是将原问题分解为相互重叠的子问题，并使用递归或迭代的方式求解子问题，然后将子问题的解组合起来得到原问题的解。与递归算法不同的是，动态规划算法会将子问题的解保存起来，避免重复计算，从而提高效率。

例如：

斐波那契数列（一个递推数列，它每个数字都是前两个数字的和，如1,1,2,3,5,8,13...）
fib(n)=fib(n-1)+fib(n-2)，fib(1)=fib(2)=1；
斐波那契数列的应用场景是走楼梯问题：站在第一级台阶，一次可以走一个或两个台阶，问走到第n级台阶时候，一共有多少种走法？走楼梯问题的数学模型就是斐波那契数列。要走到第n级台阶，分为两种情况，一种是从n-1级台阶一步走过来，另一种是从第n-2级台阶走两步走过来。所以走到第n级台阶的方法就有fib(n-1)+fib(n-2)种。


int fib(int n) {
    if(n == 1 || n == 2)return 1;//站在第一级台阶只有1种走法，第二级台阶只能从第一级台阶上来，所以第二级台阶也为1种走法
    else return (fib(n - 1) + fibi(n - 2));
}

代码的递归以2的倍数递增，复杂度为O( $eq?2%5E%7Bn%7D$ )，非常差。用DP可以优化复杂度。
为了解决总体问题fib(n)，将其分解为两个较小的子问题，即fib(n-1)和fib(n-2)，这就是DP的应用场景。
一些问题具有两个特征：重叠子问题，最优子结构。用DP可以高效率的处理具有这两个特征的问题。

1.1.1.重叠子问题

首先子问题是原大问题的小版本，计算步骤完全一样；其次，计算大问题是需要多次重复计算小问题。这就是重叠子问题，以斐波那契数列为例，递归计算fib(5)，分解成如图所示

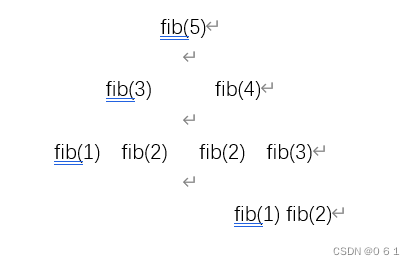
其中fib(3)计算了2次，其实只需要计算1次。
一个子问题的多次重复计算，耗费了大量时间。用DP处理重叠子问题发，每个子问题只需要计算一次，从而避免了重复计算，这就是DP效率高的原因。具体做法是得到最优子结构，然后用地推或带记忆化搜索的递归进行编程，从而实现高效的计算。

1.1.2.最优子结构

首先，大问题的最优解包含小问题的最优解；其中，可以通过小问题的最优解推导出大问题的最优解。这就是最优子结构。斐波那契问题中，把数列计算构造成fib(n)=fib(n-1)+fib(n-2)，即把原来为n的大问题，减小为n-1和n-2的小问题，这就是斐波那契数列的最优子结构。

“无后效性”

简单说，就是“未来与过去无关”。例如斐波那契数列，走到第n级台阶，有两种办法，一种是从n-1级台阶一步走过来，另一种是从第n-2级台阶走两步走过来。但是，前面是如何走到第n-1级或n-2级台阶，并不需要知道，只需它们的计算结果就行了。换句话说，只关心前面的结果，不关心前面的过程，这就是无后效性。其是DP的必要条件，因为只有这样才能降低算法的复杂度，应用DP才有意义。

1.2.DP的两种编程方法

处理DP中的大问题和小问题，有两种思路：自顶向下（Top-Down，先大问题，再小问题）、自底向上（Bottom-Up，先小问题，再大问题）。
编码实现DP时，自顶向下用带记忆化搜索的递归编码，自底向上用递推编码。两种方法的复杂度是一样的，每个子问题都计算一遍，而且只计算一遍。

1.2.1.自顶向下与记忆化

先考虑大问题，再缩小到小问题，递归很直接地体现这种思路。为了避免递归时重复计算，可以在子问题得到解决时就保存结果，再次需要这个结果时，直接返回保存的结果。


const int N = 225;
int memoize[N] = { 0 };//保存结果
int fib(int n) {
    if(n == 1 || n == 2)return 1;
    if(memoize[n] != 0)return memoize[n];//直接返回保存结果
    memoize[n] = fib(n - 1) + fib(n - 2);//递归计算，并记忆
    return memoize[n];
}

在这段代码中，一个斐波那契数列只计算了一次，所以总复杂度为O(n)。

1.2.2.自底向上与制表递推

这种方法与递归的自顶向下相反，避免了用递归编程。自底向上是先解决小问题，在解决大问题，通常通过填写多为表格来完成，编程时用若干for循环语句填表，根据表中的结果，逐步计算出大问题的解决方案。

用制表法计算斐波那契数列，维护一张一位表dp[]，记录自底向上的计算结果。


const int N = 225;
int dp[N];
int fib(int n) {
    dp[1] = dp[2] = 1;
    for(int i = 3; i <= n; i++)dp[i] = dp[i - 1] + dp[i - 2];
    return dp[n];
}

这个代码的复杂度也为O(n)。


int solve(int n) {
	int a = 1, b = 1, fib;
	for (int i = 3; i <= n; i++) {
		fib = a + b;
		a = b;
		b = fib;
	}
	cout << fib;
}

这个代码再上一个代码基础上降低了空间复杂度。

对比两种方法

自顶向下的优点时能更宏观地把握问题、认识问题的实质；自底向上的优点时编码更直接。两种方法都很常见。

1.3.DP的设计和实现（0/1背包问题）

以0/1背包问题为例，背包问题在DP中很常见，0/1背包问题是最基础的，其他背包问题都由它衍生出来。

0/1背包问题：给定n种物品和一个背包，第i个物品的体积为 $eq?c_%7Bi%7D$ ，价值为 $eq?w_%7Bi%7D$ ，背包的总容量为C。把物品装入背包时，第i个物品中只有两个选择：装入背包或不装入背包，称为0/1背包问题。如何选择装入背包的物品，使装入背包的物品总价值最大？

设 $eq?x_%7Bi%7D$ 表示物品i装入背包的情况： $eq?x_%7Bi%7D$ =0时，不装入背包； $eq?x_%7Bi%7D$ =1时，装入背包。

定义：
约束条件： $eq?%5Csum_%7Bi%3D1%7D%5E%7Bn%7Dc_%7Bi%7D*x_%7Bi%7D%5Cleqslant%20C%2Cx_%7Bi%7D%3D0%2C1$
目标函数： $eq?max%5Csum_%7Bi%3D1%7D%5E%7Bn%7Dw_%7Bi%7D*x_%7Bi%7D$

例题：

Bone collector（hdu 2606）

Problem Description

Many years ago , in Teddy’s hometown there was a man who was called “Bone Collector”. This man like to collect varies of bones , such as dog’s , cow’s , also he went to the grave …
The bone collector had a big bag with a volume of V ,and along his trip of collecting there are a lot of bones , obviously , different bone has different value and different volume, now given the each bone’s value along his trip , can you calculate out the maximum of the total value the bone collector can get ?

翻译：

题目描述：

很多年前，在Teddy的家乡，有一个被称为 "骨头收集者”的人。这个人喜欢收集各种各样的骨头，比如狗的骨头、牛的骨头，他还会去坟墓里收集骨头......
骨头收集者有一个体积为 V 的大袋子，在他的收集之旅中有很多骨头，很明显，不同的骨头有不同的价值和体积，现在给定他收集之旅中每块骨头的价值，你能算出骨头收集者能得到的总价值的最大值吗？

Input

The first line contain a integer T , the number of cases.
Followed by T cases , each case three lines , the first line contain two integer N , V, (N <= 1000 , V <= 1000 )representing the number of bones and the volume of his bag. And the second line contain N integers representing the value of each bone. The third line contain N integers representing the volume of each bone.

翻译：

输入：

第一行包含一个整数 T，即案例数。
接着是 T 个案例，每个案例三行，第一行包含两个整数 N、V，（N≤1000，V≤1000）分别代表骨头的数量和袋子的体积。第二行包含 N 个整数，代表每块骨头的价值。第三行包含 N 个整数，代表每块骨头的体积。

Output

One integer per line representing the maximum of the total value (this number will be less than 231).

翻译：

输出：

每行一个整数，代表总值的最大值（该数字将小于 231）。

Sample Input（翻译：样例输入）

1
5 10
1 2 3 4 5
5 4 3 2 1

Sample Output（翻译：样例输出）

题解

1.DP状态设计

引入一个(N+1)*(C+1)的二维数组，dp[][]，成为DP状态，dp[i][j]表示把前i个物品（从第1个到第i个）装入容量为j的背包中获取最大值。可以把每个dp[i][j]都看作一个背包：背包容量为j，装1~i这些物品。最后的dp[N][C]就是问题的答案——把N个物品装入容量为C的背包。

2.DP转移方程

用自底向上的方法计算，假设现在递推到dp[i][j]，分两种中情况：
（1）第i个物品的体积比容量j还要大，不能装进容量j的背包，那么直接继承i-1个物品装入容量为j的背包的情况即可，即dp[i][j]=dp[i-1][j]。
（2）第i个物品的体积比容量j小，能装进背包。有可以分为两种情况：装或者不装第i个物品。
<1>装第i个物品：从前i-1个物品的情况推广而来，前i-1个物品的价值为dp[i-1][j]。第i个物品装进背包后，背包容量减少c[i]，价值增加w[i]，有dp[i][j]=dp[i-1][j-c[i]]+w[i]。
<2>不装第i个物品：有dp[i][j]=dp[i-1][j]。
取两种情况中的最大值，即dp[i][j]=max(dp[i-1][j],dp[i-1][j-c[i]]+w[i])。

算法复杂度：空间复杂度O(NC)，时间复杂度O(NC)。

3.详细DP的转移过程

用一个例子详细说明。有4个物品，其体积分别为{2,3,6,5}，价值为{6,3,5,4}，背包容量为9。

步骤1：只装第1个物品。
由于物品1的体积为2，所以背包容量小于2的都不放进去，即dp[1][0]=dp[1][1]=0；容量≥2的背包都能装入，则都能放进去，dp[1][2~9]=6；

	背包容量	1	2	3	4	5	6	7	8	9
0(不装)		0	0	0	0	0	0	0	0	0
1(装第1个)		0	6	6	6	6	6	6	6	6

步骤2：只装前2个物品。
如果物品体积比背包容量大，那么不能装物品2，情况与只装第1个物品一样，故dp[2][0]=dp[2][1]=0，dp[2][2]=6；填写dp[2][3]，物品2的体积等于3，可以装入物品2，引入可以不装，如果装入物品2，则dp[2][3]=dp[1][3-3]+3=3；如果不装，dp[2][3]=dp[1][3]=6；同理装入后面的背包。

	背包容量	1	2	3	4	5	6	7	8	9
1(装第1个)		0	6	6	6	6	6	6	6	6
2(装第2个)		0	6	6	6	9	9	9	9	9

步骤3：只装前3个物品。与步骤2相同。

	背包容量	1	2	3	4	5	6	7	8	9
2(装第2个)		0	6	6	6	9	9	9	9	9
3(装第3个)		0	6	6	6	9	9	9	11	11

步骤3：只装前4个物品。与步骤2相同。

	背包容量	1	2	3	4	5	6	7	8	9
3(装第3个)		0	6	6	6	9	9	9	11	11
4(装第4个)		0	6	6	6	9	9	10	11	11

最后答案即为dp[4][9]，把四个物品装入容量为9的背包最大价值。

4.输出背包方案

	背包容量	1	2	3	4	5	6	7	8	9
0(不装)		0	0	0	0	0	0	0	0	0
1(装第1个)		0	6	6	6	6	6	6	6	6
2(装第2个)		0	6	6	6	9	9	9	9	9
3(装第3个)		0	6	6	6	9	9	9	11	11
4(装第4个)		0	6	6	6	9	9	10	11	11

倒着回头看：
dp[4][9]=max(dp[3][4]+4,dp[3][9])=dp[3][9]，说明没有装入4， $eq?x_%7B4%7D$ =0；
dp[3][9]=max(dp[2][3]+5,dp[2][9])=dp[2][3]+5，说明装入3， $eq?x_%7B3%7D$ =1；
dp[2][3]=max(dp[1][0]+3,dp[1][3])=dp[1][3]，说明没有装入2， $eq?x_%7B2%7D$ =0；
dp[1][3]=max(dp[0][1]+6,dp[0][3])=dp[0][1]+6；说明装入1， $eq?x_%7B1%7D$ =1。

5.代码展示

1.递推代码：


#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 1001;
int w[N] = { 0 }, c[N] = { 0 }, dp[N][N] = { 0 };
void solve() {
	int n, C;
	cin >> n >> C;
	memset(w, 0, sizeof(w));
	memset(c, 0, sizeof(c));
	memset(dp, 0, sizeof(dp));
	for (int i = 1; i <= n; i++) {
		cin >> w[i];
	}
	for (int i = 1; i <= n; i++) {
		cin >> c[i];
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 0; j <= C; j++) {
			if (c[i] > j)dp[i][j] = dp[i - 1][j];
			else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - c[i]] + w[i]);
		}
	}
	cout << dp[n][C] << endl;
}
int main() {
	ios::sync_with_stdio;
	cin.tie(0);
	cout.tie(0);
	int t;
	cin >> t;
	while (t--)solve();
	return 0;
}

1.4.滚动数组

滚动数组是DP最常用的空间优化技术。

DP的状态方程常常是二维和二维以上，占用太多空间。用滚动数组可以大大减少空间，可以把二位状态方程O( $eq?n%5E%7B2%7D$ )的空间复杂度优化到一维的O(n)，更高维的也可以优化后减少一维。

从状态方程dp[i][j]=max(dp[i-1][j],dp[i-1][j-c[i]]+w[i])可以看出，dp[i][]只与dp[i-1][]有关，和前面的dp[i-2]，dp[i-3]...都无关，所以可以重复利用这些空间，用新的数据覆盖无用的一行（滚动），只需要判断两行即可。

滚动数组实现的两种方式为交替滚动和自我滚动。

1.4.1.交替滚动

定义dp[2][j]，用dp[0][]与dp[1][]交替滚动，这种方法逻辑清晰不易出错。

上面例题可优化为：


#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 1001;
int w[N] = { 0 }, c[N] = { 0 }, dp[2][N] = { 0 };
void solve() {
	int n, C;
	cin >> n >> C;
	memset(w, 0, sizeof(w));
	memset(c, 0, sizeof(c));
	memset(dp, 0, sizeof(dp));
	for (int i = 1; i <= n; i++) {
		cin >> w[i];
	}
	for (int i = 1; i <= n; i++) {
		cin >> c[i];
	}
	int now = 0, old = 1;
	for (int i = 1; i <= n; i++) {
		swap(now, old);
		for (int j = 0; j <= C; j++) {
			if (c[i] > j)dp[now][j] = dp[old][j];
			else dp[now][j] = max(dp[old][j], dp[old][j - c[i]] + w[i]);
		}
	}
	cout << dp[now][C] << endl;
}
int main() {
	ios::sync_with_stdio;
	cin.tie(0);
	cout.tie(0);
	int t;
	cin >> t;
	while (t--)solve();
	return 0;
}

1.4.2.自我滚动

上面例题可优化为：


#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 1001;
int w[N] = { 0 }, c[N] = { 0 }, dp[N] = { 0 };
void solve() {
	int n, C;
	cin >> n >> C;
	memset(w, 0, sizeof(w));
	memset(c, 0, sizeof(c));
	memset(dp, 0, sizeof(dp));
	for (int i = 1; i <= n; i++) {
		cin >> w[i];
	}
	for (int i = 1; i <= n; i++) {
		cin >> c[i];
	}
	for (int i = 1; i <= n; i++) {
		for (int j = C; j >= c[i]; j--) {//放过来循环
			dp[j] = max(dp[j], dp[j - c[i]] + w[i]);
		}
	}
	cout << dp[C] << endl;
}
int main() {
	ios::sync_with_stdio;
	cin.tie(0);
	cout.tie(0);
	int t;
	cin >> t;
	while (t--)solve();
	return 0;
}

注意j反过来循环，用dp[j]'表示旧状态，dp[j]表示新状态。

（1）j从小到大循环是错误的，例如，i=2时；

dp[5]=max(dp[5],dp[5-3]+3)=9;

	背包容量	1	2	3	4	5	6	7	8	9
dp[j]'		0	6	6	6	6	6	6	6	6
dp[j]		0	6	6	6	9	6	6	6	6

dp[8]=max(dp[8],dp[5]+3)=12;此时错误。

	背包容量	1	2	3	4	5	6	7	8	9
dp[j]'		0	6	6	6	6	6	6	6	6
dp[j]		0	6	6	6	9	6	6	12	6

（2）j从大到小循环是正确的，例如，i=2时，首先计算后面的dp[9]不会修改前面的值，在使用dp[j]=max(dp[j],dp[j-c[i]]+w[i])时，dp[j-c[i]]的值没有先修改。

二维以上的数组也可以进行优化，比如dp[t][][]至于dp[t-1][][]有关，所以可以缩小为dp[2][][]或者dp[][]。

2.经典线性DP问题

2.1.分组背包

有一些物品，把物品分为n组，其中第i组的第k个物品体积为c[i][k]，价值为c[i][k]；每组内的物品冲突，每组内最多只能选择一个物品装进背包；给定一个容量为C的背包，问如何选择物品，使得装进背包的物品总价值最大。

解题思路与0/10背包问题相似。在分组背包中定义状态dp[i][j]，它表示把前i物品装入容量为j的背包（每组最多选一个物品）可获得的最大价值。状态方程为
dp[i][j]=max(dp[i-1][j],dp[i-1][j-c[i][k]]+w[i][k])
其中dp[i-1][j]表示不选第i组的物品，dp[i-1][j-c[i][k]]表示选第i组的第k个物品，求解需用三重循环，如果是滚动数组，则状态方程为
dp[j]=max(dp[j],dp[j-c[i][k]]+w[i][k])

例题

hdu 1712：ACboy needs your help

问题描述

ACboy has N courses this term, and he plans to spend at most M days on study.Of course,the profit he will gain from different course depending on the days he spend on it.How to arrange the M days for the N courses to maximize the profit?

翻译：

ACboy 本学期有 N 门课程，他计划最多花 M 天学习。当然，他将根据他花在上面的日子从不同的课程中获得的学分。如何安排N门课程的M天，实现学分最大化？

输入格式

The input consists of multiple data sets. A data set starts with a line containing two positive integers N and M, N is the number of courses, M is the days ACboy has.
Next follow a matrix A[i][j], (1<=i<=N<=100,1<=j<=M<=100).A[i][j] indicates if ACboy spend j days on ith course he will get profit of value A[i][j].
N = 0 and M = 0 ends the input.

翻译：

输入由多个数据集组成。数据集以包含两个正整数 N 和 M 的行开始，N 是课程数，M 是 ACboy 的天数。
接下来N行，表示一个矩阵 A[i][j](1≤i≤N≤100,1≤j≤M≤100)。A[i][j] 表示如果 ACboy 在第 i 门课学 j 天将获得A[i][j]学分。
N = 0 和 M = 0 结束输入。

输出格式

For each data set, your program should output a line which contains the number of the max profit ACboy will gain.

翻译：

对于每个数据集，您的程序应该输出一行，其中包含 ACboy 将获得的最大利润的数量。

样例输入

2 2
1 2
1 3
2 2
2 1
2 1
2 3
3 2 1
3 2 1
0 0

样例输出

3
4
6

题目解析

以第一个测试为例，N=M=2，第1门课程学1天得1分，学2天得2分；第2门课学1天得1分，学2天得3分；ACboy的选择是用2天学第二门课程。本题可以模拟为分组背包，每门课是一组。
物品分组：第i门课是第i组，天数是物品的体积，A[i][j]是第j个物品的价值。
背包容量：总天数M就是背包容量。

下面为自我滚动实现的代码


#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 105;
int w[N][N], c[N][N], dp[N];
void solve() {
	int n, m;
	while (1) {
		cin >> n >> m;
		if (n == 0 && m == 0) {
			break;
		}
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= m; j++) {
				cin >> w[i][j];
				c[i][j] = j;
			}
		}
		memset(dp, 0, sizeof(dp));
		for (int i = 1; i <= n; i++) {
			for (int j = m; j >= 0; j--) {
				for (int k = 1; k <= m; k++) {
					if (j >= c[i][k]) {
						dp[j] = max(dp[j], dp[j - c[i][k]] + w[i][k]);
					}
				}
			}
		}
		cout << dp[m] << endl;
	}
	
}
int main() {
	ios::sync_with_stdio;
	cin.tie(0);
	cout.tie(0);
	solve();
	return 0;
}

2.2.多重背包

给定n种物品和一个背包，第i种物品的体积为 $eq?c_%7Bi%7D$ ，价值为 $eq?w_%7Bi%7D$ ，并且有 $eq?m_%7Bi%7D$ 个，背包的总容量为C。如何选择装入背包的物品，使其装入背包中的总价值最大？

例题

波谷P1776：宝物筛选

题目描述

终于，破解了千年的难题。小 FF 找到了王室的宝物室，里面堆满了无数价值连城的宝物。
这下小 FF 可发财了，嘎嘎。但是这里的宝物实在是太多了，小 FF 的采集车似乎装不下那么多宝物。看来小 FF 只能含泪舍弃其中的一部分宝物了。
小 FF 对洞穴里的宝物进行了整理，他发现每样宝物都有一件或者多件。他粗略估算了下每样宝物的价值，之后开始了宝物筛选工作：小 FF 有一个最大载重为W的采集车，洞穴里总共有n种宝物，每种宝物的价值为 $eq?v_%7Bi%7D$ ，重量为 $eq?w_%7Bi%7D$ ，每种宝物有 $eq?m_%7Bi%7D$ 件。小 FF 希望在采集车不超载的前提下，选择一些宝物装进采集车，使得它们的价值和最大。

时间限制1.00s

内存限制125.00MB

输入格式

第一行为一个整数n和W，分别表示宝物种数和采集车的最大载重。
接下来n行每行三个整数 $eq?v_%7Bi%7D$ ， $eq?w_%7Bi%7D$ ， $eq?m_%7Bi%7D$ 。

输出格式

输出仅一个整数，表示在采集车不超载的情况下收集的宝物的最大价值。

样例输入

样例输出

提示

对于30%的数据，n≤ $eq?%5Csum%20m_%7Bi%7D$ ≤ $eq?10%5E%7B4%7D$ ，0≤W≤ $eq?10%5E%7B3%7D$ ；

对于100%的数据，n≤ $eq?%5Csum%20m_%7Bi%7D$ ≤ $eq?10%5E%7B5%7D$ ，0≤W≤4* $eq?10%5E%7B4%7D$ ，1≤n≤100。

题目解析

第一种可以将此问题转化为0/1背包问题。把相同的 $eq?m_%7Bi%7D$ 个第i种物品看作独立的 $eq?m_%7Bi%7D$ 个物品，共有 $eq?%5Csum_%7Bi%3D1%7D%5E%7Bn%7Dm_%7Bi%7D$ 个物品，然后按0/1背包问题求解，复杂度为O(C* $eq?%5Csum_%7Bi%3D1%7D%5E%7Bn%7Dm_%7Bi%7D$ )。

第二种是直接求解。定义状态dp[i][j]表示把前i个物品装进容量为j的背包，能装进背包的最大价值。第i个物品分为装或不装两种情况，得到多重背包的转移方程为
dp[i][j]=max(dp[i-1][j],dp[i-1][j-k*c[i]]+k*w[i]),(1≤k≤min(m[i],j/c[i]))
直接写i，j，k三重循环，复杂度与第一种思路相同（自我滚动的写法）。

代码如下：


#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 100010;
int v[N], w[N], m[N], dp[N];
void solve() {
	int n, W;
	cin >> n >> W;
	for (int i = 1; i <= n; i++) {
		cin >> v[i] >> w[i] >> m[i];
	}
	for (int i = 1; i <= n; i++) {
		for (int j = W; j >= w[i]; j--) {
			for (int k = 1; k <= m[i] && k * w[i] <= j; k++) {
				dp[j] = max(dp[j], dp[j - k * w[i]] + k * v[i]);
			}
		}
	}
	cout << dp[W];
}
int main() {
	ios::sync_with_stdio;
	cin.tie(0);
	cout.tie(0);
	solve();
	return 0;
}

此时会超时，所以需要进行优化，下面介绍一种优化方式。

二进制拆分优化：

这是一种简单有效的技巧。原理很简单，例如，第i种物品有 $eq?m_%7Bi%7D$ 个，这 $eq?m_%7Bi%7D$ 个物品装进背包的组合有0~ $eq?m_%7Bi%7D$ 的 $eq?m_%7Bi%7D$ +1种情况，不过，要组合成 $eq?m_%7Bi%7D$ +1种情况，其实并不需要 $eq?m_%7Bi%7D$ 个物品。根据二进制的计算原理，任何一个十进制整数X都可以用1，2，4，8等2的倍数相加而成，则 $eq?m_%7Bi%7D$ 也可以又这些组成，这些2的倍数只有 $eq?log_%7B2%7DX$ 个。题目中第i种物品有 $eq?m_%7Bi%7D$ 个，用 $eq?log_%7B2%7Dm_%7Bi%7D$ 个数就能组合出0~ $eq?m_%7Bi%7D$ 种情况，复杂度从O(C* $eq?%5Csum_%7Bi%3D1%7D%5E%7Bn%7Dm_%7Bi%7D$ )优化到O(C* $eq?%5Csum_%7Bi%3D1%7D%5E%7Bn%7Dlog_%7B2%7Dm_%7Bi%7D$ )。

注意拆分的具体实现不能全部拆成2的倍数，而是先按2的倍数从小到大拆分，最后是一个小于等于最大倍数的余数。对 $eq?m_%7Bi%7D$ 这样拆分非常有必要，能够保证拆分的数相加在[1, $eq?m_%7Bi%7D$ ]范围内，不会大于 $eq?m_%7Bi%7D$ 。

代码如下：


#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 100010;
int v[N], w[N], m[N], new_n, new_v[N], new_w[N], new_m[N], dp[N];
void solve() {
	int n, W;
	cin >> n >> W;
	for (int i = 1; i <= n; i++) {
		cin >> v[i] >> w[i] >> m[i];
	}
	new_n = 0;//二进制拆分后的新物品总数量
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m[i]; j *= 2) {//二进制枚举1，2，4，8...
			m[i] -= j;//减去已拆分的
			new_v[++new_n] = j * v[i];//新物品价值
			new_w[new_n] = j * w[i];//新物品容量
		}
		if (m[i]) {//最后一个是余数
			new_v[++new_n] = m[i] * v[i];
			new_w[new_n] = m[i] * w[i];
		}
	}
	for (int i = 1; i <= new_n; i++) {//0/1背包
		for (int j = W; j >= new_w[i]; j--) {
			dp[j] = max(dp[j], dp[j - new_w[i]] + new_v[i]);
		}
	}
	cout << dp[W];
}
int main() {
	ios::sync_with_stdio;
	cin.tie(0);
	cout.tie(0);
	solve();
	return 0;
}

这种解法可以看作多重背包的标准解法，不过还可以用单调队列来优化。

2.3.最长公共子序列（Longest Common Subsequence，LCS）

一个给定序列的子序列，是在该序列中删去若干元素后得到的序列。例如，X={A,B,C,D,A,B}，那么{A,C,D}，{A,B,A,B}都是X的子序列，子序列和子串的概念不同，子串的元素在原序列中时连续的。

给定两个子序列X和Y，当另一序列Z既是X的子序列，也是Y的子序列时，称Z是序列X和Y的公共子序列，最长公共子序列是长度最长的公共子序列。

问题描述

给定两个序列X和Y，找出X和Y的一个最长公共子序列。

问题解析

用暴力法找最长公共子序列，需要先找出X的所有子序列，然后一一验证是否为Y的最长子序列。如果X有m个元素，那么X有 $eq?2%5E%7Bm%7D$ 个子序列；Y有n个元素；总复杂度大于O(n $eq?2%5E%7Bm%7D$ )。

用动态规划求LCS，复杂度为O(nm)。用dp[i][j]表示序列 $eq?X_%7Bi%7D$ （表示 $eq?x_%7B1%7D%2Cx_%7B2%7D%2Cx_%7B3%7D%2Cx_%7B4%7D...x_%7Bi%7D$ 这个序列，即X的前i个元素组成的序列；这里的小写的x表示元素，用大写的X表示序列）和 $eq?Y_%7Bj%7D$ （表示 $eq?y_%7B1%7D%2Cy_%7B2%7D%2Cy_%7B3%7D%2Cy_%7B4%7D...y_%7Bi%7D$ 这个序列，即Y的前j个元素组成的序列）的最长公共子序列长度。dp[n][n]就是答案

分解为以下两种情况。
（1）当 $eq?x_%7Bi%7D%3Dy_%7Bj%7D$ 时，以求得 $eq?X_%7Bi-1%7D$ 和 $eq?Y_%7Bj-1%7D$ 的最长公共子序列，在其尾部加上 $eq?x_%7Bi%7D$ 或 $eq?y_%7Bj%7D$ ，即可得到 $eq?X_%7Bi%7D$ 和 $eq?Y_%7Bj%7D$ 的最长公共子序列。状态转移方程为dp[i][j]=dp[i-1][j-1]+1。
（2）当 $eq?x_%7Bi%7D%5Cneq%20y_%7Bj%7D$ 时，求解两个子问题： $eq?X_%7Bi-1%7D$ 和 $eq?Y_%7Bj%7D$ 的最长公共子序列， $eq?X_%7Bi%7D$ 和 $eq?Y_%7Bj-1%7D$ 的最长公共子序列。求取其中的最大值，其状态转移方程为，dp[i][j]=max(dp[i][j-1],dp[i-1][j])。

例题

hdu 1159：Common subsequence


#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
void solve() {
	string s1, s2;
	cin >> s1 >> s2;
	vector<vector<int>> dp(s1.length() + 1, vector<int>(s2.length() + 1));
	for (int i = 1; i <= s1.length(); i++) {
		for (int j = 1; j <= s2.length(); j++) {
			if (s1[i - 1] == s2[j - 1]) {
				dp[i][j] = dp[i - 1][j - 1] + 1;
			}
			else {
				dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
			}
		}
	}
	cout << dp[s1.length()][s2.length()] << endl;
}
int main() {
	ios::sync_with_stdio;
	cin.tie(0);
	cout.tie(0);
	solve();
	return 0;
}

2.4.最长递增子序列（Longest Increasing Subsequence，LIS）

问题描述

给定一个长度为n的数组，找出一个最长的单调递增子序列。例如：一个长度为7的序列A={5，6，7，4，2，8，3}，它的最长递增子序列为{5，6，7，8}，长度为4。

问题解析

定义状态dp[i]表示以第i个数为结尾的最长递增子序列长度，那么有
dp[i]=max(dp[i],dp[j]+1)，(0<j<i, $eq?A_%7Bj%7D%3C%20A_%7Bi%7D$ )
最终答案为max(dp[i])

复杂度为O( $eq?n%5E%7B2%7D$ )，LIS最优解不是DP，有非DP解法。

例题

洛谷 - B3637：最长上升子序列


#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 5001;
int a[N], dp[N];
void solve() {
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
		dp[i] = 1;
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= i - 1; j++) {
			if (a[j] < a[i])dp[i] = max(dp[i], dp[j] + 1);
		}
	}
	int ans = -1;
	for (int i = 1; i <= n; i++) {
		ans = max(dp[i], ans);
	}
	cout << ans;
}
int main() {
	ios::sync_with_stdio;
	cin.tie(0);
	cout.tie(0);
	solve();
	return 0;
}

2.5.数字三角形

图形

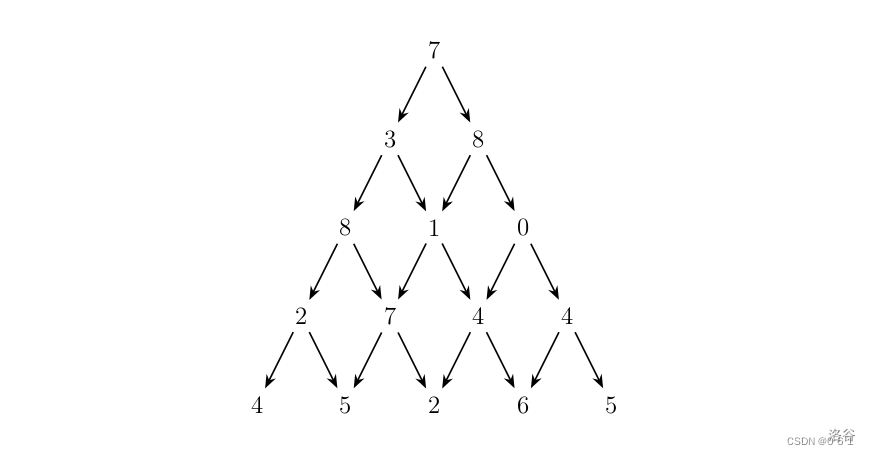
例题

波谷 P1216 ：[USACO1.5] [IOI1994]数字三角形 Number Triangles


#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 1010;
int a[N][N] = {0}, dp[N] = {0};
void solve() {
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= i; j++) {
			cin >> a[i][j];
		}
	}
	dp[1] = a[1][1];
	for (int i = 2; i <= n; i++) {
		for (int j = i; j >= 1; j--) {
			dp[j] = max(dp[j - 1], dp[j]) + a[i][j];
		}
	}
	int ans = -1;
	for (int i = 1; i <= n; i++) {
		ans = max(ans, dp[i]);
	}
	cout << ans;
}
int main() {
	ios::sync_with_stdio;
	cin.tie(0);
	cout.tie(0);
	solve();
	return 0;
}

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/天景科技苑/article/detail/836702