- 1java.security.cert.CertificateException异常的正确解决方法,亲测有效,嘿嘿嘿
- 2Git下载和安装_git 下载
- 3zookeeper is not a recognized option
- 4【11】SCI易中期刊推荐——计算机方向(中科院4区)_非oa 人工智能sci四区
- 5Pytorch实用教程:pytorch中 argmax(dim)用法详解
- 6提示词(prompt)工程指南(三):高级提示_awesome prompt
- 7Python中4种读取JSON文件和提取JSON文件内容的方法
- 8【Linux】shell编程4(break语句、continue、exit、shell的函数、返回值return)_linux break
- 9凸多边形最优三角剖分(算法设计:动态规划)_凸多边形的最优三角剖分,按照三步,采用动态规划去解决
- 10Python常用模块 之 redis:连接和操作redis数据库_python redis库
Python Sympy:解方程利器_python解方程
赞
踩
用程序来解决数学问题是非常普遍的,将数学的定理或公式封装成程序中的函数,
只要传入相应的参数,就能让计算机帮我们计算出最终的结果。
不过,今天介绍的这个库:Sympy,它的最大特点是让我们可以用做数学题的思考方式来写程序。
1. 变量和表达式
用程序实现数学的算法,会根据程序语言本身的特点来实现算法,不会像解数学问题那样一步步推导。
所以,虽然可以用程序解决很多的数学问题,但是最后将代码展现出来时,数学专业的朋友也许很难看懂。
Sympy 让我们可以用数学专业的朋友熟悉的方式来写程序。
1.1. 变量
Sympy 的变量是一个数学符号,和我们平时理解的程序中的变量不太一样。
from sympy import Symbol
x = Symbol("x")
x.name
#输出结果:
x
- 1
- 2
- 3
- 4
- 5
- 6
x是程序中的变量,它代表的数学符号也是x。
这么写可以有点迷惑,改成下面这样可能好理解一些:
a = Symbol("x")
a.name
#输出结果:
x
- 1
- 2
- 3
- 4
a是程序中的变量,它代表的数学符号是x。
1.2. 表达式
定义了数学符号之后,就可以自由的写各种数学表达式了。
比如:
x = Symbol("x")
expr = x*x + 1
print(expr)
#输出结果:
x**2 + 1
y = Symbol("y")
expr = x*x - (y-1)*(y-1)
print(expr)
#输出结果:
x**2 - (y - 1)**2
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
程序中的表达式,Sympy会转换成数学的形式,以用于数学的计算。
1.3. 因式分解和展开
因式分解是初中常做的数学题目之一,用Sympy解决这类问题非常简单。
from sympy import Symbol, factor, expand x = Symbol("x") y = Symbol("y") #分解 expr = (x-2)*(x-2) - (y-3)*(y-3) print(factor(expr)) #输出结果 (x - y + 1)*(x + y - 5) #展开 expr = (x - y + 1)*(x + y - 5) expr = expand(expr) print(expr) #输出结果 x**2 - 4*x - y**2 + 6*y - 5
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
1.4. 表达式求解
Sympy让我们可以在计算时保留数学符号(比如x,y),也可以代入实际的数字,最终求出表达式的值。
#沿用上面的表达式
print(expr)
#输出结果
x**2 - 4*x - y**2 + 6*y - 5
result = expr.subs({x:2, y:3})
print(result)
#输出结果
0
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
甚至可以用数学符号来替换,比如假设 x = y - 1 ,替换上面的表达式。
然后再求值:
expr = expr.subs({x: y - 1})
print(expr)
#输出结果
-y**2 + 2*y + (y - 1)**2 - 1
result = expr.subs({y: 3})
print(result))
#输出结果
0
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
先设置 x = y - 1,然后设 y = 3,和直接设置 x = 2, y = 3 是一样的。
所以最后计算结果也是0。
1.5. 表达式计算
Sympy 还可以支持表达式之间的计算。
#表达式之间加法
expr1 = x * y + y * y
expr2 = x * x + x * y
expr = expr1 + expr2
print(expr)
#输出结果
x**2 + 2*x*y + y**2
#因式分解
print(factor(expr))
#输出结果
(x + y)**2
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
除了加法,表达式之间也可以相减,相乘,相除也是可以的。
2. 解方程
用程序解方程问题很复杂,一般得用到牛顿迭代法之类的迭代算法。
用Sympy解方程,只要一行代码,:)
2.1. 一元方程
Sympy的solve函数封装好了方程解法。
from sympy import solve
expr = x*x - 5*x + 6
solve(expr)
#输出结果
[2, 3]
solve(expr, dict=True)
#输出结果(字典形式)
[{x: 2}, {x: 3}]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
2.2. 二元方程组
二元方程组也一样:
expr1 = 3*x + 4*y - 34
expr2 = 2*x + 3*y - 56
solve((expr1, expr2), dict=True)
#输出结果(字典形式)
[{x: -122, y: 100}]
- 1
- 2
- 3
- 4
- 5
- 6
3. 函数图像
最后,介绍下Sympy绘制函数图像的功能。
绘制函数的图像能够让我们更加直观的看到函数的变化趋势,对于理解题目非常有帮助。
使用 Sympy 绘制图像非常方便,只要传入数学表达式即可。
from sympy import plot
plot(2*x + 3)
- 1
- 2
- 3
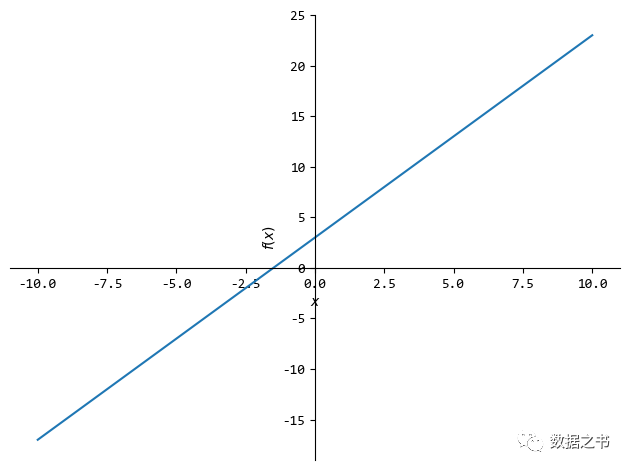
设置 X 轴的范围(-5~5):
from sympy import plot
plot(2*x + 3, (x, -5, 5))
- 1
- 2
- 3
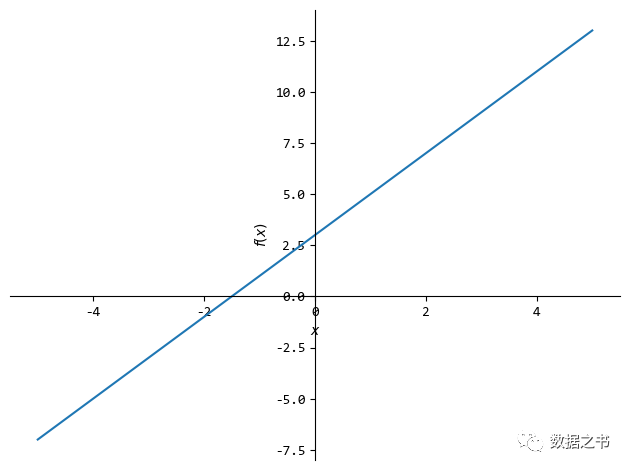
绘制多个函数的图像:
plot(2*x + 3, 5*x + 2, (x, -5, 5), legend=True)
- 1
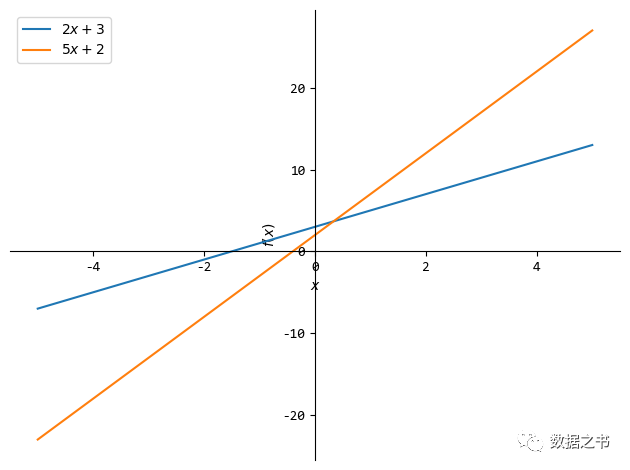
4. 总结回顾
本篇主要介绍 Sympy 在基本的代数运算方面的应用,
Sympy 最大的特点是让我们可以用数学专业的思维方式来写代码。
它的代码与数学的联系非常紧密,数学专业的朋友如果刚接触编程,用这个库来写代码一定会非常亲切。
题外话

感兴趣的小伙伴,赠送全套Python学习资料,包含面试题、简历资料等具体看下方。
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/小丑西瓜9/article/detail/645818
Copyright © 2003-2013 www.wpsshop.cn 版权所有,并保留所有权利。



