深度学习入门初步总结_深度学习初步

深度学习入门初步总结

前言

在学习深度学习之前，从某乎上看了相关的学习路线，又通过师兄们的请教，最后选择了在linux环境下，用python进行代码的编写。由于自己在这之前，对linux没有接触过，所以在安装Ubuntu以及在环境安装下还是走了不少弯路，后续会把相关的安装教程也写在博客中。在学习之前，可以说自己真的还是个小白，很多东西都不会，望以后可以和大家多多交流，一些想法可能不正确，望各位也能指出来。

一、技术储备

• python基本语法

• 由于自己之前学过python，在这里就不多做总结了

• Numpy库
  首先，numpy是python的外部库，支持大量的维度数组与矩阵运算以及大量的数学函数库。别人封装好的东西为什么不用？不过在有些库用之前，最好去扒一扒它的底层，不要仅仅停留在会用上，不然太容易被淘汰了。

  然后，numpy库可以直接通过pip3安装，下面这条命令即可

  sudo apt-get install python-numpy
  1

  其次，学会numpy的几条基本语法，其它的在有需要的时候再去问度娘，下面归纳几个经常会用到的语法。

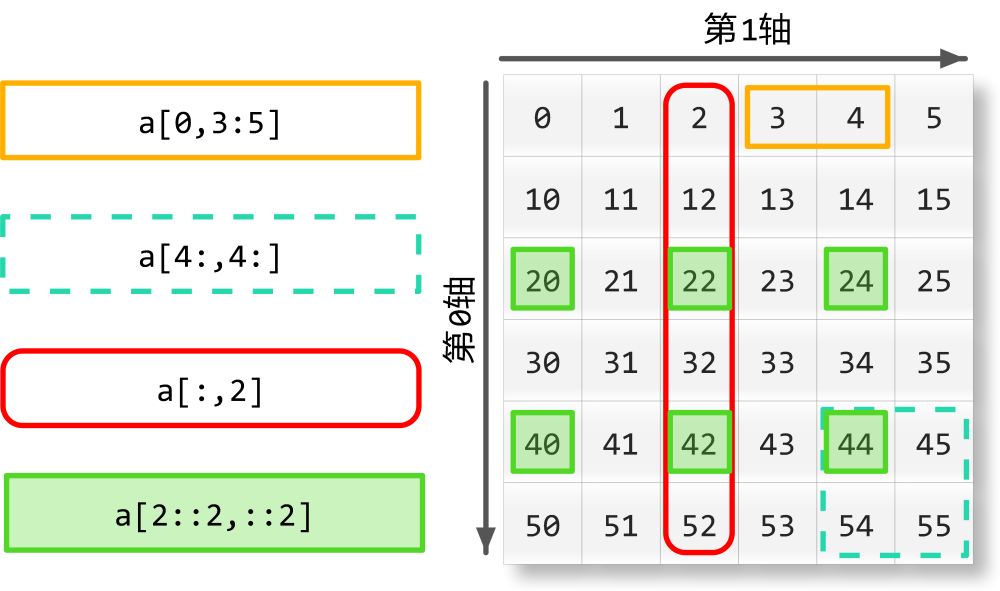
  import  numpy as np
  np.empty([3,2], dtype = int) #创建一个空的3行2列的矩阵，dtype为指定类型，默认为float类型
  np.zeros(5) #创建一个长度为5的数组
  np.zeros_like(x)#很多时候也会这样用，创建一个x大小的数组或矩阵或多维数组
  np.arange(0，100，2)#以2为单位，生成0-100的数值，很多时候都要用
  np.argmax(axis=1)#这个是找出矩阵中每一列最大的一个值，axis是偏移量，每次向下移动一个位置
  np.reshape(x,[2,3])#在不改变x数值的情况下改变x的大小，一般也可以这么用，如下：
  x.reshape(1,x.size)
  np.random.rand(2,3)#产生随机数，返回类型也是Ndarray对象
  np.random.choice(1000,100)#从0-1000中随机产生100个数
  np.ndim(x)#这个表示x的维度，比如矩阵的就为2
  X.flatten()#将x转化成一维数组
  np.dot(A,B)#计算矩阵A与矩阵B的点积
  np.sum(x,axis=0)或者np.sum(x,axis=1)#axis表示的是对不同轴的求和，如下图所示。
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13
  14

• Matplotlib库
  首先，Matplotlib的pyplot模块是绘制图形的，除了这个模块还有工具包，比如mpl_toolkits工具包，它里面有一个Axes3D模块，可以绘制相应的3D图形。其实，之前遇到遇到一个问题，为什么我早就通过pip把这些库引进来了，再新建一个项目，这些包为什么找不到？答案是新建的项目中没有引进相应的这些库，通过pip3下载的库，是保存在其它路径当中的，所以需要把这些库加载到新建的项目中即可。

  其次，通过pip3安装，如下命令（其实apt或者apt-get都可以实现，他们二者是有区别的，有兴趣可以百度）

  sudo apt-get install Matplotlib
  1

  然后，归纳了几条常用的语法结构

  import matplotlin.pylot as plt
  plt.plot(x,y,linestyle="--",label="")#x为自变量，y为函数（因变量），linestyle通常为线的类型有三种线条可以选择），label可以为这个图形添加标签
  plt.xlabel("x")或者pltylabel("y")#x,y轴标签
  plt.legend()#用于多个图例在同一个坐标中显示
  plt.show()#这个一定要加，就是把前面东西展示出来，不然会看不到图像。
1
2
3
4
5

二、神经网络

• 几个重要的概念

1. 最基本的神经网络结构分为：输入层、隐藏层、输出层
2. 权重：权重指的是输入信号的重要性的参数
3. 偏置：偏置指的是神经元被激活的容易程度
4. 激活函数：通常用h(x)来表示，这个通俗一点讲就是当输入的值达到了某个值，才会被传递到下一个神经元
5. 输出函数：输入某个值当然是想得到某个输出的值啊，其实神经网络无非就是一种算法，通过这个算法得到想要的值，再对这些值反复的进行归类，得到想要的一个模型

• 激活函数

1. sigmoid函数
   

    #python实现
    def sigmoid(x):
    s = 1 / (1 + np.exp(-x))
    return s
   
   -为什么 要使用sigmoid函数？
   
    因为通过sigmoid函数的取值范围是在0-1中，这样就可以表示事物发生的概率了，可以 满足分类的任务 
   
   1
   2
   3
   4
   5
   6
   7
   8
   9

2. 阶跃函数

    #python实现
    def step_function(x):    
    return np.array(x > 0, dtype=np.int)
   1
   2
   3

• 阶跃函数与sigmoid函数图像对比

  

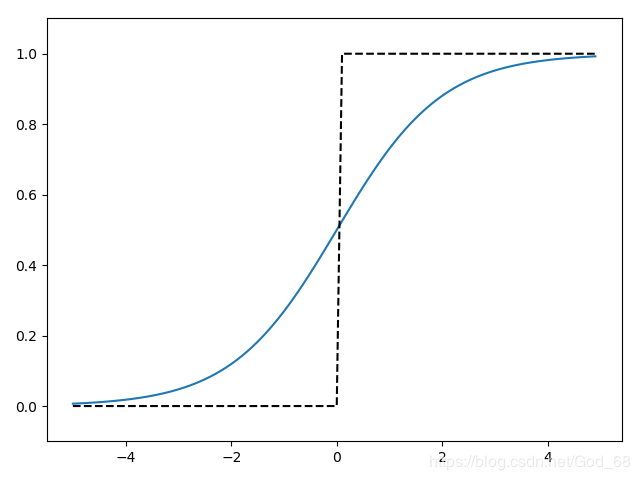
3. ReLU函数

• 实现：

  def relu(x):#G非线性函数    return np.maximum(0, x)
  1

• 问题来了？问题1：前面提到的三个激励函数都为非线性函数，那么为什么要引用非线性函数呢？

  我认为是非线性函数可以在某个范围内无限的逼近值，这样就使得可以充当下一层的输入，这样才会使得神经网络有意义。如果是线性函数的话，那就等于没有中间层了，就是原始的感知机，神经网络就没有意义了。

• 问题2：为什么引入Relu呢？（这里借用网上其它博客上的一个答案）

  第一，采用sigmoid等函数，算激活函数时（指数运算），计算量大，反向传播求误差梯度时，求导涉及除法，计算量相对大，而采用Relu激活函数，整个过程的计算量节省很多。
  第二，对于深层网络，sigmoid函数反向传播时，很容易就会出现梯度消失的情况（在sigmoid接近饱和区时，变换太缓慢，导数趋于0，这种情况会造成*信息丢失），从而无法完成深层网络的训练。
  第三，Relu会使一部分神经元的输出为0，这样就造成了网络的稀疏性，并且减少了参数的相互依存关系，缓解了过拟合问题的发生

3. 输出层的设计

• 恒等函数和softmax函数

  恒等函数是将隐藏层到输出层之间的值原样输出来，softmax输出的值都是在0-1之间，且输出值之和为1，这就可以 表示事物发生概率了。另外为了防止计算机运算上的溢出，可以将公式改进，上下同时乘以一个C，如下图所示：

  

4. 初识手写数字识别

• minist数据集

  数据集的下载，这个是运行别人写的python脚本来进行下载的，去看了看别人的源代码，大致分为从网络中下载，保存至pickle中，下一次调用直接从本地就可以获取。感兴趣的可以在我的github上下载源代码

• 我的疑惑？训练数据和测试数据都以什么形式保存呢？

  所有数据都保存至二进制文件，通过pickle保存至.pkl文件

• 正规化、预处理概念

  正规化是通过某个限定，把值限定在某个范围之内。预处理就是把输入的数据进行某种转化使得之后的数据运算变得简化的一个手段

• 批处理

  一个个去进行输入，得到输出，这样的方法太麻烦。就比如一张图片是28*28=784个像素，我们可以同时处理100张这么大像素的数据，得到100个输出值，这样就可以缩短处理的时间。

三、神经网络的学习

• 概念：神经网络中最重要的一个环节是权重，通过神经网络的自主学习从训练数据中自动获取最优权重参数的过程，学习的目的就是通过损失函数，找到最小的权重参数。

• 损失函数

  损失函数是通过预测的数据与监督数据（正确解标签）的一个函数值，表示他们二者在多大程度上差异不坏，即该性能有多好

1. 均方误差
   

• python实现：

  def mean_squared_error(y, t):    return 0.5 * np.sum((y - t) ** 2)
  1

• one-hot表示为正确标签为1，其余为0

2. 交叉熵误差
   

• 以后用到都为min-batch的交叉熵误差的实现，下面就给出mini-batch的实现，其实就是根据函数公式用python语言表示出来，弄懂基本语法就可以自己写。下面这个是摘录别人写的函数。下面这个函数主要是计算出每一行中概率最大的值并计算。

  def cross_entropy_error(y, t):#交叉熵误差，y是神经网络的输出，t是监督数据（正确解标签）
   if y.ndim == 1:#为什么要改变形状？要将数组变成（1 2 3）这种格式       
     t = t.reshape(1, t.size)        
     y = y.reshape(1, y.size)    # 监督数据是one-hot-vector的情况下，转换为正确解标签的索引    
  if t.size == y.size:      
      t = t.argmax(axis=1)#找出每一组中概率最大的一个并将其标记存入t中,t现在变成了[839]这种
  batch_size = y.shape[0]#shape[0]指的是（100,10）中的100，就是二维矩阵的行数   #print("y.shape[0]:",batch_size)    
  return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size#仅仅计算最大概率的值
  1
  2
  3
  4
  5
  6
  7
  8

3. 梯度

   首先，所有的输入值都是多维的数组（可以是一维、二维、多维），比如一张图片由784个元素组成的矩阵，那么100张图片就是100784，所以这里的这个梯度就是逐一计算每一个元素在这个点的导数值，形成梯度。其中最重要的一个性质就是梯度值指示的方向是各个点处的函数值减小最多的方向

• python中的实现

  def numerical_gradient(f, x):
      h = 1e-4  # 0.0001
      grad = np.zeros_like(x)
      it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
      while not it.finished:
          idx = it.multi_index
          tmp_val = x[idx]
          x[idx] = float(tmp_val) + h
          fxh1 = f(x)  # f(x+h)
          x[idx] = tmp_val - h
          fxh2 = f(x)  # f(x-h)
          grad[idx] = (fxh1 - fxh2) / (2 * h)
          x[idx] = tmp_val  # 还原值
          it.iternext()
      return grad
  
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13
  14
  15
  16

• 为什么要计算梯度，为了找到最优解，函数值减小最多的方向，也就是损失函数最小的方向，损失函数越小，就说明训练模型越拟合实际情况。

• 学习率 通过调整学习率可以使梯度达到一个“好的位置”，它表示在多大程度上可以更新函数

四、总结

通过前面几章的学习，自己对神经网络有了一个初步的认识，这些算法都是最经典的算法，我相信很多算法都是在这些基础上加以改进的，后面的路途遥远，还需要持之以恒。一开始学得比较慢，包括从一开始搭建linux环境，到经典算法实现的过程中，自己还是有所收获的，如果有好的想法和学习路线都可以留言给我。