图形遍历效率低？试试 R 树_r树动态更新

大家好，我是前端西瓜哥。

今天我们来看看 R 树是什么？以及它为什么能够提高图形的检索速度。

R 树（R-tree）是一种 空间索引技术，能够是从大量的节点中，快速找到特定范围的元素集合，而不用一个不落地遍历所有节点。

思路和其他索引算法（比如 B 树、跳表）有点像，但 R 树针对的是高维数据的查询 。R 树的 “R” 指的是矩形（Rectangle）。

举个具体的例子，假设有一张地图，上面有几百万个节点，要快速找某个位置半径 2 公里的所有餐馆的信息。

低效的做法是遍历这几百万的节点的位置，判断距离是否小于 2 公里。

但如果用上索引技术，比如 R 树，我们就能利用索引去 空间换时间，快速拿到特定范围的节点超集，比如几千个。

接着只需要遍历这几千个节点去判断符合条件的节点就可以了，而不需要完完整整遍历所有的节点。

除此之外还可以：

1. 快速检索平面中和选区矩形相交的二维图形；
2. 在数据库中快速找出多维度的产品，比如价格、库存、过期时间在特定范围的商品。

R 树的数据结构

下面看一下在图形编辑器的一个场景。

我们构建了一棵图形树，图形树的图形有位置、宽高等属性，并渲染在画布上。

需要实现选择功能，绘制一个矩形选区，使和该选区矩形相交的图形高亮。

为实现这个能力，我们计算图形树上的每个图形的包围盒：一个用 minX，minY、maxX、maxY 表达的一个矩形，它刚好包围住图形。

包围盒的作用是简化碰撞算法，一些复杂的图形，比如贝塞尔曲线，如果要严格意义上判断碰撞，是要进行复杂的计算的，在有大量图形的场景下，性能非常糟糕。

所以业内常用矩形包围盒的碰撞来简化，这种算法非常简单高效，可直接用来替代原本复杂精细的碰撞检测，或是在进行复杂碰撞算法前先做一层过滤，避免无谓的复杂运算。

// 矩形是否相交
function intersects(a, b) {
  return b.minX <= a.maxX &&
         b.minY <= a.maxY &&
         b.maxX >= a.minX &&
         b.maxY >= a.minY;
}
1
2
3
4
5
6
7

这个包围盒特点，就很适合拿来应用 R 树来提高图形树的 检索效率。

R 树的数据结构是一个平衡树。

和其他索引树类似，R 树的叶子节点是数据节点，保存有图形信息和它的最小包围矩形（MBR）。

最小包围矩形其实就是包围盒。

结构大概类似这样：

{
  minX: 20,
  minY: 40,
  maxX: 30,
  maxY: 50,
  // 保存图形数据，比如图形对象 id，或图形对象本身
  data: {}
};
1
2
3
4
5
6
7
8

R 树会将距离相近的数据节点收集起来，并放到同一个父节点下。这个父节点是 索引节点，不会保存图形信息，但会记录子节点的合并的包围盒数据。

父节点如果多了，也会把它们收集起来，放到一个新的父节点下。

这样就形成了一个树的结构。

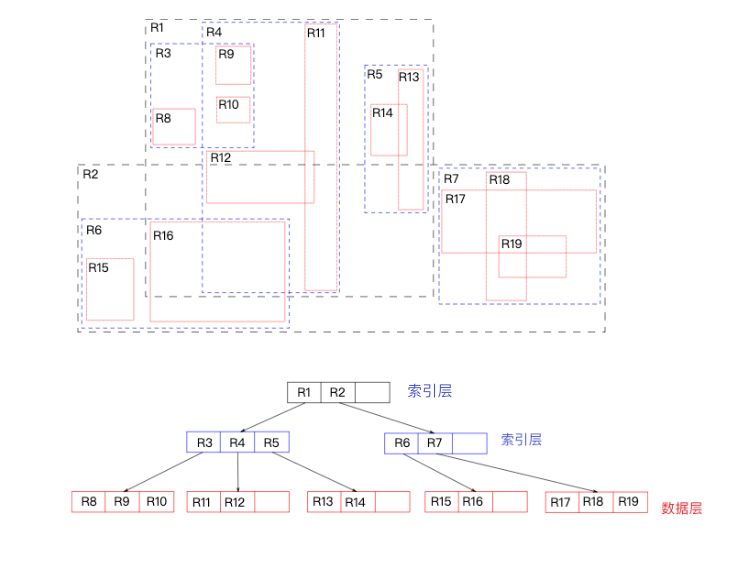
实际生产环境，推荐使用一个名为 RBush 的高性能 NPM 库。

代码用法示例：

import RBush from "rbush";

// 创建一个 R 树实例
const tree = new RBush();

// 也可以指定一个索引节点最多有几个子节点，默认是 9 个
const tree2 = new RBush(16);
1
2
3
4
5
6
7

R 树的检索

检索的过程如下：

提供一个选区矩形，从根节点开始，往下递归查找判断选取矩形是否和当前节点矩形相交。

1. 若不相交，其下的节点也不会相交，该节点对应的子树就不需要继续递归了；
2. 若相交且为数据节点（叶子节点），将其放到 result 数组；
3. 若是包含关系，其下的所有数据节点放到 result 数组；
4. 若相交但并不包含，则遍历其下的的子节点，重复前面的操作。

直到可能相交的节点遍历完结束，然后返回 result 数组。

RBush 的搜索写法：

const result = tree.search({
  minX: 20,
  minY: 20,
  maxX: 80,
  maxY: 70,
});
1
2
3
4
5
6

其源码实现：

class RBush {
  // ...

  search(bbox) {
    let node = this.data;
    const result = [];

    if (!intersects(bbox, node)) return result;

    const toBBox = this.toBBox;
    const nodesToSearch = [];

    while (node) {
      for (let i = 0; i < node.children.length; i++) {
        const child = node.children[i];
        const childBBox = node.leaf ? toBBox(child) : child;

        if (intersects(bbox, childBBox)) {
          // 1. 遍历到数据节点
          if (node.leaf) result.push(child);
          // 2. 索引节点
          // 2.1. 包含关系，索引节点下的所有数据节点都加进 result
          else if (contains(bbox, childBBox)) this._all(child, result);
          // 2.2. 相交不包含关系，继续判断相交
          else nodesToSearch.push(child);
        }
      }
      node = nodesToSearch.pop();
    }

    return result;
  }
  
  _all(node, result) {
    const nodesToSearch = [];
    while (node) {
      if (node.leaf) result.push(...node.children);
      else nodesToSearch.push(...node.children);

      node = nodesToSearch.pop();
    }
    return result;
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

R 树的更新

1、初始化

在图形编辑器初始化的时候，我们要计算图形树所有图形的包围盒，然后插入到 R 树上。

RBush 插入单个节点的写法：

const item = {
  minX: 20,
  minY: 40,
  maxX: 30,
  maxY: 50,
  graphId: '123',
};

tree.insert(item);
1
2
3
4
5
6
7
8
9

支持批量插入节点，RBush 针对批量添加做了优化，效率比单个插入更高。

tree.load([item1, item2, /* ... */]);
1

2、更新

R 数作为索引数据，是要实时更新。

为此，我们需在每次图形物理属性改变的时候，重新计算包围盒，并更新 R 树。

tree.remove(item);
tree.insert(newItem);
1
2

四叉树（Quadtree）

还有一种同样可以减少遍历节点数量的算法，叫做 四叉树（Quadtree）碰撞检测。

四叉树将视口界面分割成多个区域，每个区域记住自己包含了哪些图形。

然后移动目标图形时，判断它落在哪个区域，取出所在区域的图形，这些图形集合就是和目标图形发生碰撞图形的超集。

当一个区域的图形数量过多时，又会进行分裂，再次分成 4 个区域。

四叉树详细讲解可以看我的这篇文章：

《快速检索碰撞图形：四叉树碰撞检测》

四叉树更适合图形均匀分布的场景，如果不均匀，会产生大量空节点，且查询效率会降低。

R 树除了处理二维，还可以处理更高维度的数据，相比四叉树更适合范围查询。

结尾

我是前端西瓜哥，欢迎关注我，学习更多图形知识。